Für einen individuellen Ausdruck passen Sie bitte die Einstellungen in der Druckvorschau Ihres Browsers an. Regelwerk, Strahlenschutz

Verabschiedet in der 283. Sitzung der Strahlenschutzkommission am 15./16. September 2016

1 Hintergrund

Im Rahmen der Überarbeitung der Norm DIN 6815:2005-05 "Medizinische Röntgenanlagen bis 300 kV - Regeln für die Prüfung des Strahlenschutzes nach Errichtung, Instandsetzung und wesentlicher Änderung" durch den Normenausschuss Radiologie im DIN wurde angeregt, einen neuen Abschnitt zum Umgang mit Messergebnissen und deren Messunsicherheiten bei technischen Prüfungen einzufügen. Die Norm DIN 6815 hat eine besondere Bedeutung, da die Richtlinie für Sachverständigenprüfungen nach Röntgenverordnung und andere Normen auf sie verweisen. Einsprüche im Normungsverfahren haben dazu geführt, dass der im Entwurf zunächst neu eingebrachte Abschnitt mit Festlegungen zur Messunsicherheit in der 2013 erschienenen Fassung wieder gestrichen wurde. Es wurde jedoch die Notwendigkeit gesehen, die Berücksichtigung von Messunsicherheiten bei messtechnischen Prüfungen zukünftig zu betrachten und die Diskussion unabhängig von der Norm fortzuführen.

Infolgedessen hat das BMUB die SSK beauftragt, eine Empfehlung zur Berücksichtigung von Messunsicherheiten bei der Durchführung von messtechnischen Prüfungen im Strahlenschutz zu erarbeiten. Hierbei sollte insbesondere berücksichtigt werden,

• dass sich "Anforderungen sowohl aus gesetzlichen Grenzwerten als auch aus nach dem Stand der Technik bzw. dem Stand von Wissenschaft und Technik zu erfüllenden Schutzanforderungen ergeben können" und
• "in wie weit Vorgaben zur Größe der zulässigen Messunsicherheiten erforderlich sind und durch wen diese aus fachlicher Sicht festgelegt werden sollten".

Über den genannten Anwendungsbereich hinaus ist bei Messungen im Rahmen des praktischen Strahlenschutzes und der Überwachung der Umweltradioaktivität vielfach ein Vergleich von Messwerten mit Anforderungswerten vorzunehmen. In all diesen Fällen soll die vorliegende Empfehlung der SSK bestehende Unklarheiten im Vollzug beseitigen und ein einheitliches Vorgehen bei Prüfungen der Konformität mit Anforderungen ermöglichen.

2 Problemstellung

Im Bereich des Strahlenschutzes werden bei messtechnischen Prüfungen die Anforderungen vielfach durch Toleranzbereiche definiert, die durch gesetzliche Grenzwerte oder durch technische Mindestanforderungen in Richtlinien und Normen vorgegeben werden. Ziel einer messtechnischen Prüfung ist es festzustellen, ob ein Toleranzbereich über- bzw. unterschritten und damit eine Anforderung nicht eingehalten wird.

Dabei ist es möglich, dass sich der erzielte Messwert innerhalb des Toleranzbereiches befindet, der wahre Wert der Messgröße jedoch außerhalb des Toleranzbereiches liegt. Zur Beurteilung dieses Sachverhalts ist die Angabe des vollständigen Messergebnisses erforderlich. Neben dem Messwert als Schätzwert für den der Messung zugrundeliegenden wahren Wert ist die Angabe der Messunsicherheit erforderlich.

Um eine Bewertung der Messergebnisse bezüglich der Einhaltung von Anforderungen vornehmen zu können, ist festzulegen, wie die Messunsicherheiten zu berücksichtigen sind.

3 Empfehlungen

Zur Berücksichtigung der Messunsicherheit bei der messtechnischen Überprüfung der Konformität mit Anforderungen empfiehlt die SSK:

1. Das Ergebnis einer messtechnischen Prüfung muss die Angabe des Messwertes y und der Standardmessunsicherheit u(y) beinhalten. ¹
   
2. Die Bestimmung der Standardmessunsicherheit hat entsprechend dem "Guide to the expression of uncertainty in measurement" (GUM) (JCGM 100) oder dem Supplement 1 zum GUM (JCGM 101) zu erfolgen.
   
   Alternativ zur Bestimmung der Standardmessunsicherheit nach GUM oder GUM Supplement 1 dürfen nachvollziehbare konservative Abschätzungen der Messunsicherheiten durchgeführt werden. Dazu dürfen Angaben aus anderen Quellen (Richtlinien, Normen, Vorschläge von Fachgesellschaften etc.) herangezogen werden.
   
   Die Standardmessunsicherheit des Messwertes ist vom Prüfer zu ermitteln. Die Ermittlung der Standardmessunsicherheit ist zu dokumentieren.
   
   Dort, wo die Voraussetzungen zur Ermittlung der Standardmessunsicherheiten derzeit noch nicht in vollem Umfang gegeben sind, wird empfohlen, Informationen zur Ermittlung der Standardmessunsicherheiten unter Berücksichtigung aller Beiträge zur Unsicherheit zu erarbeiten.
   
3. Anforderungen beziehen sich immer auf den wahren Wert y~ einer Messgröße Y. Da der wahre Wert einer Messgröße aber unbekannt und unerkennbar ist und nur durch einen Messwert y geschätzt wird, können nur Wahrscheinlichkeitsaussagen über den wahren Wert gemacht werden. Eine Anforderung wird als erfüllt angesehen, wenn dies mit hoher Wahrscheinlichkeit der Fall ist. Mit der Festlegung der Überdeckungswahrscheinlichkeiten gemäß den nachstehenden Empfehlungen liegen die Wahrscheinlichkeiten für richtige Entscheidungen zugunsten von Konformität jeweils mindestens bei 95 % und für falsche Entscheidungen maximal bei 5 %. Die SSK hält dies für sachgerecht (siehe wissenschaftliche Begründung).
   
4. Sind Anforderungen durch einen einseitig nach oben begrenzten Toleranzbereich mit einer oberen Schranke T_o festgelegt, unter der der wahre Wert der Messgröße mit hoher Wahrscheinlichkeit liegen soll, dann soll auf Konformität entschieden werden, wenn die obere Grenze ² des probabilistisch symmetrischen Überdeckungsintervalls ³ mit einer Überdeckungswahrscheinlichkeit von 90 % kleiner ist als die Schranke T_o.
   
   Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gilt damit bei einer relativen Unsicherheit kleiner 25 % die Bedingung für Konformität

   y + 1, 65 ⋅ u(y) < T_o.

   Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 (ISO 11929 ) bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.
   

5. Sind Anforderungen durch einen einseitig nach unten begrenzten Toleranzbereich mit einer unteren Schranke T_u festgelegt, oberhalb der der wahre Wert der Messgröße mit hoher Wahrscheinlichkeit liegen soll, dann soll auf Konformität entschieden werden, wenn die untere Grenze ⁴ des probabilistisch symmetrischen Überdeckungsintervalls mit einer Überdeckungswahrscheinlichkeit von 90 % größer ist als die Schranke T_u.
   
   Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gilt damit bei einer relativen Unsicherheit kleiner 25 % die Bedingung für Konformität

   y - 1, 65 ⋅ u(y) > T_u.

   Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 (ISO 11929 ) bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.
   

6. Sind Anforderungen durch einen zweiseitig begrenzten Toleranzbereich [T_u, T_o].festgelegt, in dem der wahre Wert der Messgröße mit hoher Wahrscheinlichkeit liegen soll, dann soll auf Konformität entschieden werden, wenn der probabilistisch symmetrische Überdeckungsbereich mit einer Überdeckungswahrscheinlichkeit von 95 % innerhalb des Toleranzbereichs liegt ⁵.
   
   Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gelten damit bei relativen Unsicherheiten kleiner 25 % die Bedingungen für Konformität

   y - 1, 96 ⋅ u(y) > T_u und y + 1, 96 ⋅ u(y) < T_o.

   Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 (ISO 11929 ) bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.
   

7. Die Frage im Beratungsauftrag "inwieweit Vorgaben zur Größe der zulässigen Messunsicherheiten erforderlich sind und durch wen diese aus fachlicher Sicht festgelegt werden sollten" wird wie folgt beantwortet:
   Anforderungen aus dem Regelwerk sind über Toleranzbereiche festgelegt ⁶ oder festzulegen. Vorgaben zur Größe der zulässigen Messunsicherheiten sind beim Vorgehen nach dieser Empfehlung nicht erforderlich.
   
8. Die Festlegung eines Konformitätsbereichs [ K_u, K_o ] setzt die Kenntnis der Standardmessunsicherheit als Funktion des primären Messergebnisses und eine hinreichende Reproduzierbarkeit der Messungen einschließlich der Standardmessunsicherheiten voraus. ⁷ Der Konformitätsbereich ist dann definiert über die impliziten Gleichungen:
   
   1. für einen einseitig nach oben begrenzten Toleranzbereich:

      P(y~ > T_o / y = K_o, u (y = K_o)) = 0,05.

      Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gilt damit bei relativen Unsicherheiten kleiner 25 % die Bedingung für die Grenze des Konformitätsbereichs

      K_o = T_o - 1,65 ⋅ u (y = K_o) .

      Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 (ISO 11929 ) bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.
      

   2. für einen einseitig nach unten begrenzten Toleranzbereich:

      P(y~ < T_u /y = K_u, u (y = K_u)) = 0,05.

      Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gilt damit bei relativen Unsicherheiten kleiner 25 % die Bedingung für die Grenze des Konformitätsbereichs

      K_u = T_u + 1,65 ⋅ u (y = K_u) .

      Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 (ISO 11929 ) bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.
      

   3. für einen zweiseitig begrenzten Toleranzbereich:

      P(y~ < T_u / y = K_u, u (y = K_u)) + P(y~ > T_o / y = K_o, u (y = K_o)) = 0,05.

      Ohne Beschränkung der relativen Messunsicherheit des Messverfahrens gelten damit die Bedingungen für die Grenzen des Konformitätsbereichs:

      P(y~ < T_u / y = K_u, u (y = K_u)) = 0,025 und P(y~ > T_o / y = K_o, u (y = K_o)) = 0,025.

      Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gelten damit bei relativen Unsicherheiten kleiner 25 % die Bedingungen für die Grenzen des Konformitätsbereichs

      K_u = T_u + 1,96 ⋅ u (y = K_u und K_o = T_o - 1,96 ⋅ u (y = K_o) .

      Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 (ISO 11929 ) bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.

4 Wissenschaftliche Begründung

4.1 Grundlagen

Die aktuellen Entwicklungen der Metrologie haben zu einem international akzeptierten Verfahren zur Definition und Quantifizierung von Messunsicherheiten geführt. Es begann in den 1990er Jahren mit dem ISO Guide to the Expression of Uncertainty in Measurement (GUM) (ISO 1993) und der Normenreihe DIN 1319 (DIN 1996, 1999). Eine Bayessche Theorie der Messunsicherheiten (Weise und Wöger 1993) diente als theoretische Grundlage des GUM. Diese Theorie benutzt das Bayes Theorem und die Produktregel, um die erforderlichen Wahrscheinlichkeitsdichten aufzustellen und fortzupflanzen. Nach anfänglichen Akzeptanzproblemen und vielfältigen Diskussionen wurde der GUM durch das Joint Committee on Guides in Metrology (JCGM) erneut publiziert (JCGM 100) und erweitert (JCGM 101). Heute ist die Methodik, die im GUM und seinen Anhängen dargestellt ist, international anerkannt und stellt den Stand von Wissenschaft und Technik in der Behandlung von Unsicherheiten in der Metrologie dar.

Das JCGM hat auch Empfehlungen zur Berücksichtigung von Messunsicherheiten bei der Beurteilung der Konformität von Messwerten mit Anforderungen ausgesprochen (JCGM 106). Die vorliegende Empfehlung der SSK ist mit JCGM (2012b) konform.

Bei Radioaktivitätsmessungen wurde die Umsetzung des GUM und seine Anwendung zur Bestimmung charakteristischer Grenzen wie der Erkennungsgrenze, der Nachweisgrenze und der Grenzen des Überdeckungsintervalls in ISO 11929 bzw. DIN ISO 11929 genormt (ISO 11929 ). Auf diese Normen wird sowohl in Normen zur Überwachung der Umweltradioaktivität als auch im deutschen und internationalen Regelwerk Bezug genommen. ISO 11929 bzw. DIN ISO 11929 bieten das Handwerkszeug zur Anwendung der in Kapitel 3 empfohlenen Vorgehensweise.

In der Metrologie stellt sich das Konzept der Unsicherheit wie folgt dar: Durch eine Messung erhält man einen unsicheren Schätzwert y (Messergebnis) des unbekannten und nicht erkennbaren wahren Wertes y~ der Messgröße Y. Dann beschreibt die bedingte Wahrscheinlichkeitsdichtefunktion f_y (y~ / y, ℑ) , d. h. die Wahrscheinlichkeit, dass, gegeben das Messergebnis y und jede sonst noch verfügbare Information ℑ , der wahre Wert der Messgröße Y gerade y~ ist, vollständig die Unsicherheit, die mit dem Messergebnis y verbunden ist. f_y (y~ / y, ℑ) ist die Wahrscheinlichkeitsdichtefunktion (PDF = probability density function) einer Zufallsvariablen, die als Schätzer von Y dient. Als eine PDF ist sie auf Eins normalisiert

= 1. Anstatt der PDF fy (y~ / y, ℑ) , die die Unsicherheit vollständig beschreibt,

kann die Unsicherheit auch durch ein Überdeckungsintervall [ y^<, y^> ] charakterisiert werden, das den wahren Wert der Messgröße mit einer vorgewählten Überdeckungswahrscheinlichkeit
(1 - y) enth´lt. Als sogenannte Standardmessunsicherheit u(y) wird die Wurzel aus der Varianz der PDF f_y (y~ / y, ℑ) bezeichnet.

Die PDF hängt von der verfügbaren Information ab. Der GUM - nicht so explizit - und explizit das GUM Supplement 1 (JCGM 101) benutzen das Prinzip der maximalen Informationsentropie (PME), um verschiedenste PDFs abzuleiten, abhängig von der jeweils verfügbaren Information. Wenn lediglich das Messergebnis y und die ihm zugeordnete Standardmessunsicherheit uy) verfügbar sind, ist die resultierende PDF die Normalverteilung N(y, u (y)) .

Die SSK schließt sich den Empfehlungen des JCGM an und empfiehlt die Anwendung des GUM und des GUM Supplement 1 (JCGM 100, JCGM 101) zur Quantifizierung von Messunsicherheiten. Für die Beurteilung der Konformität mit Anforderungen empfiehlt die SSK die Methodik in (JCGM 106).

Aus Schutzvorschriften entsprechend dem Stand von Wissenschaft und Technik sowie aus gesetzlichen Grenzwerten ergeben sich Anforderungen an technische Prüfungen. Diese können in Form von ein- oder zweiseitig begrenzten Toleranzbereichen für verschiedene Parameter festgelegt werden. Zum Nachweis der Einhaltung der Anforderungen ist ein messtechnischer Nachweis zu führen. Um eine gesicherte Aussage treffen zu können, ist die Berücksichtigung der Messunsicherheit von entscheidender Bedeutung. Unter Messunsicherheit wird hier die einem Messwert y zugeordnete Standardmessunsicherheit uy) gemäß JCGM (2008a, 2008b) verstanden.

Es wird die Entscheidung getroffen, dass die Anforderung erfüllt ist, d. h. dass der Messwert mit den Anforderungen konform ist, wenn im Fall eines festgelegten Toleranzbereichs der wahre Wert der Messgröße mit einer festzulegenden Wahrscheinlichkeit innerhalb des Toleranzbereichs liegt.

Aus der wissenschaftlichen Bewertung einer Messaufgabe können lediglich Randbedingungen für die benötigten Wahrscheinlichkeiten abgeleitet werden. Die Festlegung muss durch den Regelgeber erfolgen, sie ist gesellschaftliche Übereinkunft.

Die SSK empfiehlt (Empfehlung 3), die Wahrscheinlichkeit für eine richtige Entscheidung bei Konformitätsprüfungen mit 95 % festzulegen. Damit liegt die Wahrscheinlichkeit für eine falsche Entscheidung bei 5 %. Der Wert von 5 % wird im internationalen Normenwerk vielfach zitiert und ist angesichts der eingeschränkten Möglichkeiten, sehr hohe Perzentile von Wahrscheinlichkeitsdichtefunktionen zuverlässig zu bestimmen, sinnvoll.

Die Festlegung der Grenzen eines Toleranzbereichs hat so zu erfolgen, dass die Wahrscheinlichkeit von 5 % für eine falsche Entscheidung zugunsten von Konformität im Hinblick auf das Schutzziel tolerabel ist.

Mit dem Konzept der Messunsicherheiten nach dem GUM und dem GUM Supplement 1 können mittels Quantilen der PDF f_y (y~ / y, ℑ)  die obigen Entscheidungsregeln in den folgenden Abschnitten präzisiert werden.

Die Anforderung gilt als erfüllt, d. h. dass der Messwert mit den Anforderungen konform ist,

1. wenn im Fall eines festgelegten, einseitig durch eine untere oder obere Schranke begrenzten Toleranzbereichs die untere bzw. obere Grenze des Überdeckungsbereichs zur Überdeckungswahrscheinlichkeit 90 % größer bzw. kleiner ist als diese Schranke,
2. wenn im Fall eines festgelegten zweiseitig begrenzten Toleranzbereichs der Überdeckungsbereich zur Überdeckungswahrscheinlichkeit 95 % innerhalb des Toleranzbereichs liegt.

Die Berechnung der Überdeckungsbereiche kann im Falle der Anwendung des GUM mittels der Standardmessunsicherheiten u(y) und Quantilen der Standardnormalverteilung k_1-a, z.B. nach DIN ISO 11929 (ISO 11929 ), erfolgen. Im Falle der Anwendung des GUM Supplement 1 sind numerische Verfahren zur Ermittlung der Grenzen der Überdeckungsbereiche erforderlich.

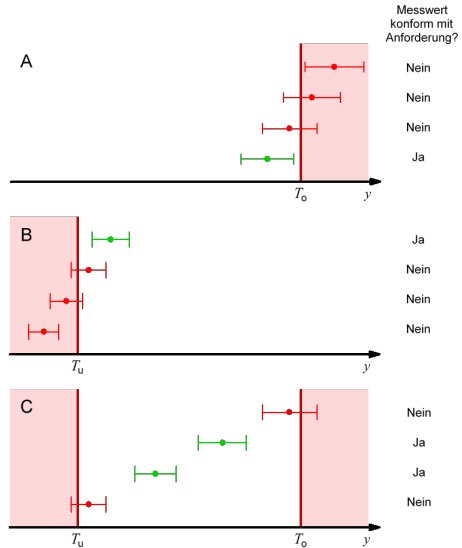
Im Einzelnen ergeben sich damit zur Berücksichtigung der Messunsicherheit bei der messtechnischen Überprüfung der Konformität mit Anforderungen die in Kapitel 3 dargestellten Empfehlungen der SSK, die in Kapitel 4 erläutert und begründet werden. Abbildung 1 erläutert die in den Empfehlungen in Kapitel 3 festgelegten Entscheidungsregeln.

Abb. 1: Prüfung der Konformität mit Anforderungen für einen einseitig nach oben beschränkten Toleranzbereich (A), einen einseitig nach unten beschränkten Toleranzbereich (B) und einen zweiseitig beschränkten Toleranzbereich (C). Die SSK empfiehlt Überdeckungswahrscheinlichkeiten (in der Abbildung jeweils als Spannbreite der Messpunkte dargestellt) von 90 % in den Fällen A und B und 95 % im Fall C. Dieser Empfehlung liegt das Kriterium zugrunde, dass die Wahrscheinlichkeit für eine richtige Entscheidung zugunsten von Konformität mindestens 95 % betragen soll und die Wahrscheinlichkeit für eine falsche Entscheidung 5 % nicht übersteigen soll.

4.2 Ableitung und Erläuterungen der Empfehlungen

Anforderungen werden vielfach durch Festlegung von Toleranzbereichen [T_u, T_o] für die wahren Werte einer Messgröße festgelegt. Es wird gefordert, dass der wahre Wert der Messgröße y~ in diesem Intervall liegt. Da der wahre Wert einer Messgröße unbekannt und unerkennbar ist, können nur Wahrscheinlichkeitsaussagen über ihn gemacht werden. Vielfach wird auch ein Konformitätsintervall [K_u, K_o] festgelegt. Liegt ein Messwert y im

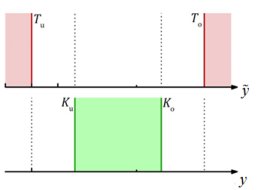
Konformitätsintervall, wird entschieden, dass Konformität mit den Anforderungen vorliegt. Abbildung 2 stellt die Konzepte des Toleranzintervalls und des Konformitätsintervalls schematisch für einen zweiseitig begrenzten Toleranzbereich dar.

Die Festlegung eines Konformitätsbereichs [K_u, K_o] zur Beurteilung der Konformität mit Anforderungen setzt die Kenntnis der Standardmessunsicherheit u(y) als Funktion des primären Messergebnisses und eine hinreichende Reproduzierbarkeit der Messungen einschließlich der Messunsicherheiten voraus. Der Konformitätsbereich ist dann definiert über die impliziten Gleichungen; siehe Abschnitt 4.2.3 und 4.2.4

Abb. 2: Toleranzbereich für den wahren Wert y~, gegeben durch die Grenzen T_u und T_o, und Konformitätsbereich für Messwerte y, gegeben durch K_u und K_o; vgl. auch Fig. 1 in (JCGM 106).

4.2.1 Konformität bei einseitig begrenzten Toleranzbereichen

Sind Anforderungen durch einen einseitig nach oben begrenzten Toleranzbereich mit einer oberen Schranke T_o festgelegt, unter der der wahre Wert der Messgröße mit hoher Wahrscheinlichkeit liegen soll, dann soll auf Konformität entschieden werden, wenn die obere Grenze des probabilistisch symmetrischen Überdeckungsintervalls mit einer Überdeckungswahrscheinlichkeit von 90 % kleiner ist als die Schranke T_o.

Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gilt damit bei einer relativen Unsicherheit kleiner 25 % die Bedingung für Konformität

y + 1, 65 ⋅ u(y) < T_o.

Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.

Sind Anforderungen durch einen einseitig nach unten begrenzten Toleranzbereich mit einer unteren Schranke Tu festgelegt, oberhalb der der wahre Wert der Messgröße mit hoher Wahrscheinlichkeit liegen soll, dann soll auf Konformität entschieden werden, wenn die untere Grenze des probabilistisch symmetrischen Überdeckungsintervalls mit einer Überdeckungswahrscheinlichkeit von 90 % größer ist als die Schranke Tu.

Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gilt damit bei einer relativen Unsicherheit kleiner 25 % die Bedingung für Konformität

y - 1, 65 ⋅ u(y) > T_u.

Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 (ISO 11929 ) bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.

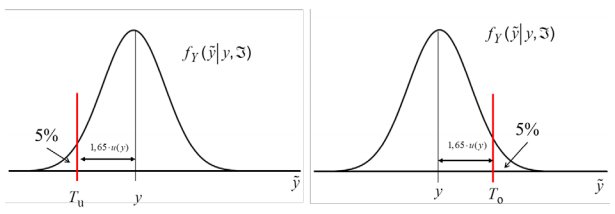
Zur Erläuterung der in den Empfehlungen 4 und 5 gemachten Festlegungen für den Nachweis von Konformität werden in Abbildung 3 die Extremfälle für die verschiedenen Konformitätsprüfungen schematisch vorgestellt, die sicherstellen, dass mit den jeweiligen Überdeckungswahrscheinlichkeiten die Wahrscheinlichkeit einer richtigen Entscheidung zugunsten von Konformität mindestens 95 % und die einer falschen Entscheidung kleiner 5 % sein soll.

Die Forderung eines symmetrischen Überdeckungsintervalls zu einer Wahrscheinlichkeit von nur 90 % resultiert aus dem Umstand, dass stets nur eine Seite der Verteilung die Möglichkeit hat, wahre Werte unterhalb bzw. oberhalb der Toleranzgrenze T_u bzw. T_o zu liefern. Die andere Seite liefert auch außerhalb des Überdeckungsintervalls wahre Werte, die konform zu den Anforderungen sind.

Die Frage im Beratungsauftrag "inwieweit Vorgaben zur Größe der zulässigen Messunsicherheiten erforderlich sind und durch wen diese aus fachlicher Sicht festgelegt werden sollten" wird wie folgt beantwortet:

Anforderungen aus dem Regelwerk sind über Toleranzbereiche festgelegt oder festzulegen. Vorgaben zur Größe der zulässigen Messunsicherheiten sind daher nicht erforderlich.

Abb. 3: Extremfälle bei einseitig begrenzten Toleranzbereichen. Bei einseitig begrenzten Toleranzbereichen genügt es, eine Überdeckungswahrscheinlichkeit von 90 % für das probabilistisch symmetrische Überdeckungsintervall zu fordern, um die Wahrscheinlichkeit für falsche Entscheidungen zugunsten von Konformität kleiner als 5 % zu halten.

4.2.2 Konformität bei zweiseitig begrenztem Toleranzbereich

Sind Anforderungen durch einen zweiseitig begrenzten Toleranzbereich [T_u, T_o] festgelegt, in dem der wahre Wert der Messgröße mit hoher Wahrscheinlichkeit liegen soll, dann soll auf Konformität entschieden werden, wenn der probabilistisch symmetrische Überdeckungsbereich mit einer Überdeckungswahrscheinlichkeit von 95 % innerhalb des Toleranzbereichs liegt:

P(y~ < T_u v y~ > T_o / y, u(y)) < 0,05.

Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gelten damit bei relativen Unsicherheiten kleiner 25 % die Bedingungen für Konformität

y - 1, 96 ⋅ u(y) > T_u und y + 1, 96 ⋅ u(y) < T_o.

Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 (ISO 11929 ) bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.

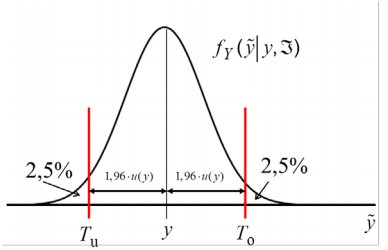
Die Festlegung der Überdeckungswahrscheinlichkeit mit 95 % ist konservativ und stellt für jede relative Messunsicherheit die Einhaltung der 5 %igen Wahrscheinlichkeit für falsche Entscheidungen sicher. Verdeutlicht wird der Grenzfall für die implizit maximal mögliche Standardmessunsicherheit und der daraus resultierenden Forderung nach einer Überdeckungswahrscheinlichkeit von 95 % in Abbildung 4. Messverfahren mit einer höheren Messunsicherheit sind nicht in der Lage, den Nachweis der Einhaltung der Anforderungen zu liefern.

Abb. 4: Extremfall bei zweiseitig begrenztem Toleranzbereich, der es notwendig macht, bei dieser Anforderung die Überdeckungswahrscheinlichkeit mit 95 % anzusetzen. In diesem Extremfall ist die Unsicherheit so groß, dass das probabilistisch symmetrische Überdeckungsintervall zur Wahrscheinlichkeit 95 % gerade den gesamten Toleranzbereich ausfüllt.

4.2.3 Konformitätsbereich bei einseitig begrenzten Toleranzbereichen

Die Festlegung eines Konformitätsbereichs [K_u, K_o] setzt die Kenntnis der Standardmessunsicherheit als Funktion des primären Messergebnisses und eine hinreichende Reproduzierbarkeit der Messungen einschließlich der Standardmessunsicherheiten voraus. Der Konformitätsbereich ist dann definiert über die implizite Gleichung:

• für einen einseitig nach unten begrenzten Toleranzbereich [T_u, + ∞]
• wird nur die untere Grenze des Konformitätsbereichs K_u benötigt:

P(y~ < T_u / y = K_u, u(y = K_u)) = 0,05.

Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gilt damit bei relativen Unsicherheiten < 25 % die Bedingung K_u = T_u + 1, 65 ⋅ u(y = K_u) (siehe Abb. 5):

• für einen einseitig nach oben begrenzten Toleranzbereich [0, T_o]
• wird nur die obere Grenze des Konformitätsbereichs K_o benötigt:

P(y~ > T_o / y = K_o, u(y = K_o)) = 0,05.

Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gilt damit bei relativen Unsicherheiten < 25 % die Bedingung K_o = _To - 1, 65 ⋅ u(y = K_o) (siehe Abb. 5).

Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 (ISO 11929 ) bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.

Abb. 5: Schematische Darstellung zur Erläuterung der Festlegungen zum Konformitätsbereich bei einseitig nach oben oder nach unten begrenzten Toleranzbereichen.

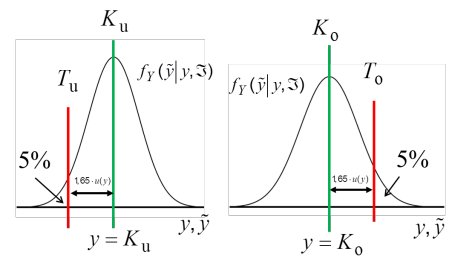
4.2.4 Konformitätsbereich bei zweiseitig begrenztem Toleranzbereich

Die nachfolgenden Betrachtungen beziehen sich auf die konservative Festlegung nach Abschnitt 4.2.2.

Bei einem zweiseitig begrenzten Toleranzbereich [T_u, T_o] folgt für den Konformitätsbereich [K_u, K_o]:

P(y~ < T_u / y = K_u, u(y = K_u)) = 0,025 und P(y~ > T_o / y = K_o, u(y = K_o)) = 0,025.

Dabei wurde berücksichtigt, dass die Wahrscheinlichkeit für falsche Entscheidungen zugunsten von Konformität sich symmetrisch verteilt (siehe Abb. 6).

Falls der GUM (JCGM 100) zur Ermittlung der Messunsicherheit benutzt wird, gelten damit bei relativen Unsicherheiten kleiner 25 % die Bedingungen

K_u = T_u + 1, 96 ⋅ u(y = K_u) und K_o = T_o - 1,96 ⋅ u(y = K_o).

Bei größeren relativen Unsicherheiten siehe DIN ISO 11929 (ISO 11929 ) bzgl. der Berechnung der Grenzen des Überdeckungsintervalls.

Abb. 6: Schematische Darstellung zur Erläuterung der Festlegungen zum Konformitätsbereich.

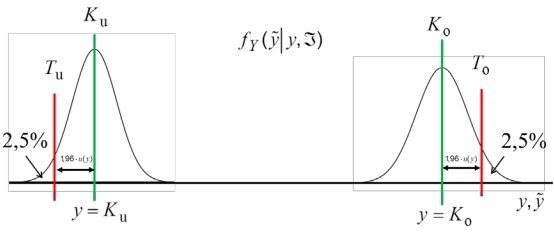
5 Literatur

.

A-1 Definitionen

Konformitätsbereich [K_u, K_o ] (acceptance interval), (JCGM 106):

Bereich zulässiger Messwerte im Sinne der Erfüllung von Anforderungen

Messergebnis (JCGM 200):

Menge von Größenwerten, die einer Messgröße zugewiesen sind, zusammen mit jeglicher verfügbarer relevanter Information ((JCGM 200), 2.9)

ANMERKUNG 1 ⁸ (JCGM 200): Ein Messergebnis enthält im Allgemeinen "relevante Informationen" über die Menge der Größenwerte, von denen einige repräsentativer für die Messgröße sein können als andere. Dies kann in Form einer Wahrscheinlichkeitsdichtefunktion ausgedrückt werden.

ANMERKUNG 2 (JCGM 200): Ein Messergebnis wird im Allgemeinen als ein einziger Messwert und eine Messunsicherheit ausgedrückt. Wird die Messunsicherheit für einige Zwecke als vernachlässigbar angesehen, kann das Messergebnis als ein einziger Messwert ausgedrückt werden. In vielen Bereichen ist dies die übliche Art, ein Messergebnis auszudrücken.

Messunsicherheit (JCGM 200):

nichtnegativer Parameter, der die Streuung der Werte kennzeichnet, die der Messgröße auf der Grundlage der benutzten Informationen beigeordnet sind

ANMERKUNG 1 (JCGM 200): Die Messunsicherheit schließt Komponenten ein, die sich aus systematischen Effekten ergeben wie Komponenten, die mit Korrektionen und den zugewiesenen Größenwerten von Normalen zusammenhängen, sowie die Eigenunsicherheit. Manchmal werden geschätzte systematische Effekte nicht korrigiert, sondern es werden stattdessen beigeordnete Messunsicherheitsbeiträge berücksichtigt.

ANMERKUNG 2 (JCGM 200): Der Parameter kann beispielsweise sein: eine Standardabweichung, genannt Standardmessunsicherheit (oder ein vorgegebenes Vielfaches davon), oder die halbe Spannweite eines Intervalls mit einer angegebenen Überdeckungswahrscheinlichkeit.

Messwert y (JCGM 200):

Größenwert, der ein Messergebnis repräsentiert

ANMERKUNG 4 (JCGM 200): Im GUM werden die Benennungen "Messergebnis" und "Schätzwert des Wertes der Messgröße" oder auch nur "Schätzwert der Messgröße" für , Messwert" verwendet.

Standardmessunsicherheit u(y) (JCGM 200):

Messunsicherheit, ausgedrückt als eine Standardabweichung.

Toleranzbereich [T_u, T_o] (JCGM 106):

Bereich, in dem der wahre Wert mit hoher Wahrscheinlichkeit liegen muss, damit die zu erfüllenden Anforderungen eingehalten werden.

Überdeckungsintervall (JCGM 200):

Intervall, das die Menge der wahren Werte einer Messgröße mit einer angegebenen Wahrscheinlichkeit enthält, auf der Grundlage der verfügbaren Informationen.

ANMERKUNG 2 (JCGM 200): Ein Überdeckungsintervall sollte nicht "Vertrauensintervall" genannt werden, um Verwechslungen mit dem statistischen Begriff zu vermeiden (siehe (JCGM 100), 6.2.2)

ANMERKUNG 3 (JCGM 200): Ein Überdeckungsintervall kann von einer erweiterten Messunsicherheit abgeleitet sein (siehe (JCGM 100), 2.3.5).

Überdeckungsintervall, probabilistisch symmetrisches [y^<, y^>] :

Überdeckungsintervall mit der Eigenschaft x P(y~ < y^< / y, u(y)) = P(y~ > y^> /  y, u(y)) = y / 2

Überdeckungswahrscheinlichkeit (JCGM 200):

Wahrscheinlichkeit 1 - y,  dass der wahre Wert einer Messgröße in einem spezifizierten Überdeckungsintervall enthalten ist

wahrer Wert y~ (JCGM 200):

Größenwert, der mit der Definition einer Größe in Übereinstimmung ist

ANMERKUNG 1 (JCGM 200): Im Messabweichungsansatz zur Beschreibung von Messungen wird davon ausgegangen, dass ein wahrer Wert einer Größe eindeutig, aber in der Praxis nicht ermittelbar ist. Der Unsicherheitsansatz erkennt an, dass aufgrund der naturgegeben unvollständigen Detailkenntnisse in der Definition einer Größe es nicht nur einen einzigen wahren Wert einer Größe gibt, sondern eine Menge an wahren Werten, die mit der Definition konsistent sind. Jedoch ist es im Prinzip und in der Praxis nicht möglich, diese Werte zu kennen. Andere Ansätze verzichten ganz auf den Begriff des wahren Wertes und beziehen sich auf den Begriff der metrologischen Verträglichkeit von Messergebnissen, um ihre Gültigkeit zu beurteilen.

ANMERKUNG 3 (JCGM 200): Wenn angenommen werden kann, dass die der Messgröße beigeordnete Eigenunsicherheit im Vergleich zu den anderen Komponenten der Messunsicherheit vernachlässigbar ist, kann davon ausgegangen werden, dass die Messgröße einen "im Wesentlichen einzigen" wahren Wert hat. Dies ist der Ansatz des GUM und der sich darauf beziehenden Dokumente, wobei das Wort "wahr" als überflüssig angesehen wird.

A-2 Größen und Symbole

Größen werden durch Großbuchstaben bezeichnet. Sie müssen sorgfältig von ihren Werten unterschieden werden, die durch die entsprechenden Kleinbuchstaben bezeichnet werden. Hier werden die Größen und Symbole nach ISO 11929 bzw. DIN ISO 11929 (ISO 11929 ) benutzt.

A-3 Beispiele

A-3.1 Dosisleistungsmessung mit einseitig nach oben begrenztem Toleranzbereich

An der Grenze eines Sperrbereichs soll durch eine Messung der Ortsdosisleistung H´*(10) überprüft werden, ob das Kriterium der Strahlenschutzverordnung eingehalten ist, dass die Ortsdosisleistung an der Grenze des Sperrbereichs 3 mSv/h nicht überschreiten darf. Es handelt sich somit um einen einseitig nach oben begrenzten Toleranzbereich mit T_o (H´* (10)) = 3 mSv/h .

Zur Messung wird ein geeichtes Ortsdosimeter mit Geiger-Müller-Zählrohr benutzt. Die relative Unsicherheit der Messung wurde durch unabhängige Wiederholungsmessungen in einem vergleichbaren Strahlungsfeld als relative Standardabweichung der angezeigten Messwerte zu u_rel (H´* (10)) = 0,08 bestimmt. ⁹

Die Messung ergab eine Ortsdosisleistung von H´* (10) = 2,70 mSv/h. Die zugeordnete Standardmessunsicherheit ist

u(H´* (10)) = H´* (10) u_rel (H´* (10)) = 2,70 mSv/h 0,08 = 0,22 mSv/h.

Nach Empfehlung 4 kann auf Konformität mit der Anforderung erkannt werden, wenn y + 1, 65 ⋅ u(y) < T_o erfüllt ist. Das heißt, es muss gelten:

H´* (10) + 1, 65 ⋅ u (H´* (10)) < T_o (H´* (10)) = 3 mSv/h.

Dies ist nicht der Fall, da

2,70 mSv / h + 1,65 ⋅ 0,22 mSv/h = 3,06 mSv/h T_o (H´* (10)) = 3 mSv/h

ist.

Nach Erweiterung des Sperrbereichs wird an der Grenze zum Sperrbereich eine Ortsdosisleistung von H´* (10) = 2,50 mSv/h gemessen mit einer Standardmessunsicherheit von

u(H´* (10)) = H´* (10) u_rel (H´* (40)) = 2,50 mSv/h ⋅ 0,08 = 0,20 mSv/h.

Nunmehr ist mit

2,50 mSv/h + 1, 65 ⋅ 0,20 mSv/h = 2,83 mSv/h < T_o (H´* (10)) = 3 mSv/h

die Abgrenzung des Sperrbereichs konform mit der Anforderung der Strahlenschutzverordnung.

Mit der Information, dass die relative Standardmessunsicherheit unter diesen Messbedingungen u_rel (H´* (10)) = 0,08 beträgt, kann auch ein Konformitätsbereich angegeben werden. Für einen einseitig nach oben begrenzten Toleranzbereich muss für den Konformitätsbereich gemäß Empfehlung 8.a gelten:

K_o = T_o - 1,65 ⋅ u (y = K_o) .

⋅ Dies bedeutet in diesem Beispiel für die obere Grenze des Konformitätsbereichs

werden die Anforderungen der Strahlenschutzverordnung erfüllt.

A-3.2 Messung der Dosisleistung in der Ebene des Bildempfängers bei medizinischen Röntgeneinrichtungen zur Durchleuchtung nach DIN 6868-150 mit einseitig nach oben begrenztem Toleranzbereich

Im Rahmen der Abnahmeprüfungen von medizinischen Röntgeneinrichtungen wird die Dosisleistung in der Ebene des Bildempfängers nach der DIN 6868-150 ¹⁰ gemessen. Für Röntgeneinrichtungen mit einem Flachdetektor mit einer Kantenlänge von 25 cm (längste Kante) bzw. für Röntgeneinrichtungen mit einem Bildverstärker mit einem Bezugsformat von 25 cm muss laut DIN 6868-150 ein Grenzwert für die Bildempfängerdosisleistung K´_B in der Ebene des Bildempfängers von 0,6 µGy/s eingehalten werden. Es handelt sich somit um einen einseitig nach oben begrenzten Toleranzbereich T_o (K´_B) = 0,60 µ Gy/s .

Zur Messung der Bildempfängerdosisleistung wird ein geeichtes Diagnostikdosimeter verwendet. Die relative Unsicherheit der Messung wurde durch unabhängige Wiederholungsmessungen in vergleichbaren Strahlungsfeldern als relative Standardabweichung der angezeigten Messwerte zu u_rel (K´_B) = 0,11 bestimmt.

Die Messung ergab eine Bildempfängerdosisleistung in der Ebene des Bildempfängers von K´_B = 0,42 µ Gy/s. Die zugeordnete Standardmessunsicherheit beträgt

u(K´_B) = K´_B ⋅ ur_el (K´_B) = 0,42 µ Gy/s ⋅ 0,11 = 0,05 ∝ Gy/s.

Gemäß Empfehlung 4 wird auf Konformität mit der Anforderung entschieden, wenn y + 1,65 ⋅ u(y) < T_o erfüllt ist. Das heißt, es muss gelten:

K´_B + 1, 65 ⋅u(K´_B) < T_o (K´_B) = 0,60 µ Gy/s.

Es gilt in diesem Beispiel:

0,42 µ Gy/s + 1,65 ⋅ 0,05 µ Gy/s = 0,50 µ Gy/s < 0,60 µ Gy/s .

Damit ist die Röntgeneinrichtung konform mit der Anforderung.

Da aus unabhängigen Wiederholungsmessungen in vergleichbaren Strahlungsfeldern eine konstante relative Messunsicherheit angenommen werden kann, kann auch ein Konformitätsbereich angegeben werden. Für einen einseitig nach oben begrenzten Toleranzbereich muss für den Konformitätsbereich gemäß Empfehlung 8.a gelten:

K_o = T_o - 1,65 ⋅ u(y = K_o) .

Dies bedeutet in diesem Beispiel für die obere Grenze des Konformitätsbereichs

werden die Anforderungen erfüllt.

A-3.3 Aktivitätsmessung mit beidseitig begrenztem Toleranzbereich

Für eine Schilddrüsenfunktionsuntersuchung sollen 70 MBq Tc-99m mit einem beidseitig begrenzten Toleranzbereich von ± 15% aus einem Generator abgefüllt werden. Damit liegen die Grenzen des beidseitig begrenzten Toleranzbereichs bei

T_u (A) = 59,50 MBq und T_o (A) = 80,50 MBq.

Um die Konformität mit der Anforderung zu überprüfen, wird die abgefüllte Aktivität in einem Messplatz gemessen. Bei der unabhängigen Kalibrierung des Messplatzes wurde eine konstante relative Standardmessunsicherheit von u_rel (A) = 0,05 ermittelt.

Die Messung ergab einen Messwert von A = 67,00 MBq mit einer Standardmessunsicherheit

u(A) = A ⋅ u_rel = (A) ⋅ 67,00 MBq ⋅ 0,05 = 3,35 MBq.

Gemäß Empfehlung 6 wird auf Konformität mit der Anforderung entschieden, wenn gilt

y - 1, 96 ⋅ u(y) > T_u und y + 1,96 ⋅ u(y) < T_o.

Damit lautet die Bedingung im aktuellen Beispiel:

A - 1, 96 ⋅ u(A) > T_u (A) und A + 1,96⋅ u(A) < T_o (A).

Mit dem obigen Messwert und der ihm zugeordneten Standardmessunsicherheit ergibt sich

A - 1,96 ⋅ u(A) = 67,00 MBq - 1,96 ⋅ 3,35 MBq = 60,43 MBq > T_u(A) = 59,50 MBq

und

A + 1,96 ⋅ u(A) = 67,00 MBq + 1,96 ⋅ 3,35 MBq = 73,57 MBq < T(A) = 80,50 MBq .

Damit ist die abgefüllte Aktivität konform mit der Anforderung.

Da aus Kalibriermessungen eine konstante relative Messunsicherheit angenommen werden kann, kann auch ein Konformitätsbereich angegeben werden. Nach Empfehlung 8.c gilt:

K_u = T_u + 1,96 ⋅ u (y = K_u) und K_o = T_o 1,96 ⋅ u (y = K_o) .

Dies bedeutet in diesem Beispiel für die Grenzen des Konformitätsbereichs

und

1) Die Symbole werden hier als Platzhalter für Symbole von physikalischen Größen benutzt. Bei der Anwendung dieser Empfehlung sind die jeweiligen Symbole der Größen zu verwenden; siehe Beispiele im Anhang.

2) Die obere Grenze des probabilistisch symmetrischen Überdeckungsbereichs zur Überdeckungswahrscheinlichkeit von 90 % ist das 95. Perzentil der Wahrscheinlichkeitsdichtefunktion f_Y (y~/y, ℑ) ; siehe Kapitel 4.

3) Der Begriff "Überdeckungsintervall" wird hier anstatt des in der frequentistischen Statistik üblichen Begriffs "Konfidenzintervall" benutzt, um den zugrundeliegenden Bayesschen Ansatz zu verdeutlichen. Das probabilistisch symmetrische Überdeckungsintervall zur Wahrscheinlichkeit (1y) wird durch die Nebenbedingung definiert, dass mit der Wahrscheinlichkeit y/2 der wahre Wert jeweils unterhalb der unteren und oberhalb der oberen Grenze des Überdeckungsintervalls liegt. Der Begriff wird hier zur Abgrenzung zum kürzesten Überdeckungsintervall benutzt.

4) Die untere Grenze des probabilistisch symmetrischen Überdeckungsintervalls ist das 5. Perzentil der Wahrscheinlichkeitsdichtefunktion f_Y (y~/y, ℑ) ; siehe Kapitel 4.

5) Die Festlegung der Überdeckungswahrscheinlichkeit mit 95 % ist konservativ und stellt für jede relative Messunsicherheit die Einhaltung der 5 %igen Wahrscheinlichkeit für falsche Entscheidungen sicher.

6) Ein Toleranzbereich ist ein Bereich zulässiger Werte einer Messgröße. Die Festlegung der Grenzen eines Toleranzbereichs hat im Regelwerk zu erfolgen und hängt von den Konsequenzen ab, die eine Abweichung vom festgelegten Bereich hat.

7) Informationen über die Messunsicherheit als Funktion des primären Messergebnisses können zum Beispiel aus unabhängig durchgeführten Messungen stammen oder in Normen vorgegeben sein. Sie können jedoch auch im Einzelfall durch Ermittlung der aktuellen Messunsicherheiten erlangt werden.

8) Die Nummerierung der Anmerkungen entspricht der der jeweiligen Zitatstelle.

9) Bei einem geeichten Messgerät ist die Frage, wie gut das Messgerät die Messgröße abbildet, nicht relevant für die Standardmessunsicherheit eines Messwertes.

10) DIN 6868-150. Sicherung der Bildqualität in röntgendiagnostischen Betrieben - Teil 150: Abnahmeprüfungen nach der Röntgenverordnung an medizinischen Röntgeneinrichtungen für Aufnahme und Durchleuchtung. Juni 2013

ENDE