 Für einen individuellen Ausdruck passen Sie bitte die
Für einen individuellen Ausdruck passen Sie bitte dieEinstellungen in der Druckvorschau Ihres Browsers an. Regelwerk

 Für einen individuellen Ausdruck passen Sie bitte die Für einen individuellen Ausdruck passen Sie bitte dieEinstellungen in der Druckvorschau Ihres Browsers an. Regelwerk |  |
TRD 301 Anlage 1 - Berechnung auf Wechselbeanspruchung durch schwellenden Innendruck bzw. durch kominierte Innendruck- und Temperaturänderung
- Berechnung -
Technische Regeln für Dampfkessel (TRD)
Ausgabe April1975
(ArbSch. 7-8/1975 S. 301;1-2/1978 S. 59; 4/1978 S.121; 9/1978 S. 310; BArbBl. 3/1980 S. 58; 5/1986 S. 51; 7-8/1996 S. 78 aufgehoben)
Vorbemerkung
Für die Berechnung auf Wechselbeanspruchung sind örtliche Spannungspitzen maßgebend. Bei statischer Beanspruchung werden diese nur mittelbar über Mittelspannung und zugehörige Verschwächungsbeiwerte, die eine begrenzte teilplastische Verformung berücksichtigen, erfaßt
1. Geltungsbereich
1.1. Diese Anlage 1 zu TRD 301 gilt für die Nachrechnung von Bauteilen, die nach TRD 301 ausgelegt wurden, im Hinblick auf wechselnde Beanspruchungen, die durch Innendruck einerseits und radiale Temperaturdifferenzen beim Anfahren (Aufheizen) und beim Abfahren (Abkühlen) andererseits an den hierdurch höchstbeanspruchten Stellen entstehen 1.
Es wird vorausgesetzt, daß bei druckführenden und temperaturbeanspruchten Bauteilen die größten örtlichen Spannungsspitzen an der Innenseite der Lochränder von Ausschnitten oder an Abzweigen In Zylinderschalen auftreten. Zusätzliche Kräfte und Momente nennenswerter Größe müssen gesondert berechnet werden (Regeln zur Zeit in Vorbereitung).
Die folgenden Berechnungsregeln werden noch in dem Maße vervollständigt, wie neue Erkenntnisse gewonnen werden.
1.2. Die Berechnung geht von den tatsächlich ausgeführten Abmessungen des betreffenden Anlagenteiles aus, die durch Nachmessen festzustellen sind. Ist die tatsächlich ausgeführte Wanddicke nicht bekannt, so ist die wahrscheinliche Wanddicke wie folgt zu berechnen:
Ist die Wanddicke se eine mittlere Wanddicke, so gilt als Berechnungswanddicke sb = se. Ist se eine Mindestwanddicke, so ist bei nahtlosen Zylinderschalen sb = 1,15 ⋅ se und bei geschweißten Mänteln aus Blech sb = se + 1 einzusetzen 2.
Gleichzeitig gilt, je nachdem ob di oder da als Nenndurchmesser vorliegt:
da = di + 2 sb
di = da - 2 sb
dm = 0,5 (da + di)
1.3. Für die Berechnung wird während einer betrachteten An- und Abfahrperiode (Lastzyklus) als maßgebende Temperatur ϑ* definiert:
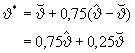 (1)
(1)
Alle temperaturabhängigen Größen sind auf diese maßgebende Zyklustemperatur ϑ* des betreffenden Lastzyklus zu beziehen 3.
1.4. Wegen der annähernd linearen Abhängigkeit der Spannungen vom maßgebenden Innendruck p* kann die Berechnung der zulässigen Temperaturdifferenzen allein auf die zwei Punkte des minimalen und maximalen Druckes des betrachteten Lastzyklus beschränkt werden. Zwischenwerte sind dann linear zu interpolieren.
2. Berechnungsgrößen und -einheiten
Siehe TRD 301 Abschnitt 2.
3. Einzelspannungen
3.1. Ideal-elastische mechanische Lochrandspannungen
3.1.1. Die maximale Lochrandspannung für Zylinderschalen mit senkrechten Abzweigen wird nach folgender Beziehung ermittelt:
σip = αm ⋅ p* dm/2sb (2)
Für die Formzahl αm gilt
αm = αm0 + fu ⋅ αb (3)
Falls αm bzw. die Formzahl αm0 weder durch Messungen noch durch Rechnung bestimmt wurden, ist einzusetzen:
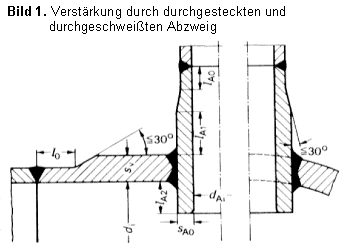
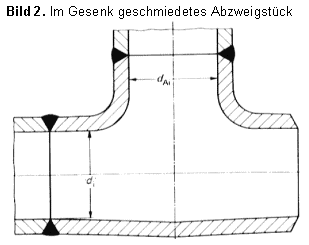
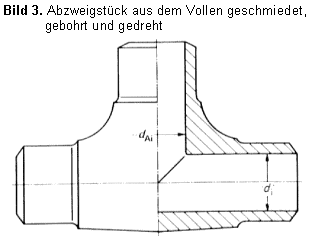
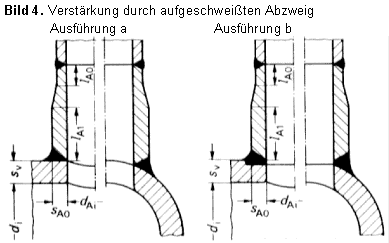
| αm0 = 2,6 | für durchgesteckte und durchgeschweißte Abzweige, Bild 1, sowie für im Gesenk geschmiedete Abzweige mit kegeligem Übergang und Ausrundung, Bilder 2 und 3, jeweils ohne Restspalt |
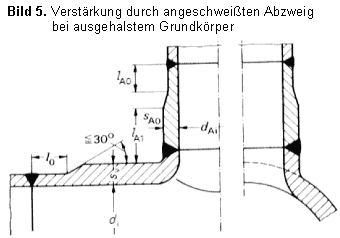
| αm0 = 2,9 | für aufgeschweißte Abzweige; Aufsatzfläche angepaßt oder ebengefräst; Wurzel ausgebohrt oder überschliffen, ohne Restspalt, Bild 4
Abweichend hiervon kann für dAi < 50 mm; dAi/di < 0,2 und 1,6 < sA0/sv < 2,0 die Formzahl αm0 = 2,4 gesetzt werden. |
| αm0 = 3,2 | für ausgehalste Grundkörper mit angeschweißtem Abzweig; Wurzel ausgebohrt oder überschliffen, ohne Restspalt, Bild 5 |
| αm0 = 5,0 | für Walz- oder Walz/Schweißverbindungen |
Sind die Anforderungen an die Schweißverbindung nicht erfüllt, z.B. bei unbearbeiteter Schweißwurzel oder einem Restspalt < 1,5 mm, so ist αm0 um den Faktor für den Einfluß des Wurzelspaltes
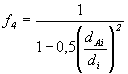 (4)
(4)
zu erhöhen. Bei Durchmesserverhältnissen dAi/di; > 0,5 und zugleich di > 300 mm sind jedoch die Anforderungen nach (1) grundsätzlich einzuhalten. Wurzelspalte >1,5 mm sind unzulässig.
(2) Falls die Formzahl αb weder durch Messungen noch durch Rechnung bestimmt wurde, gilt für alle Abzweige αb = 2,0.
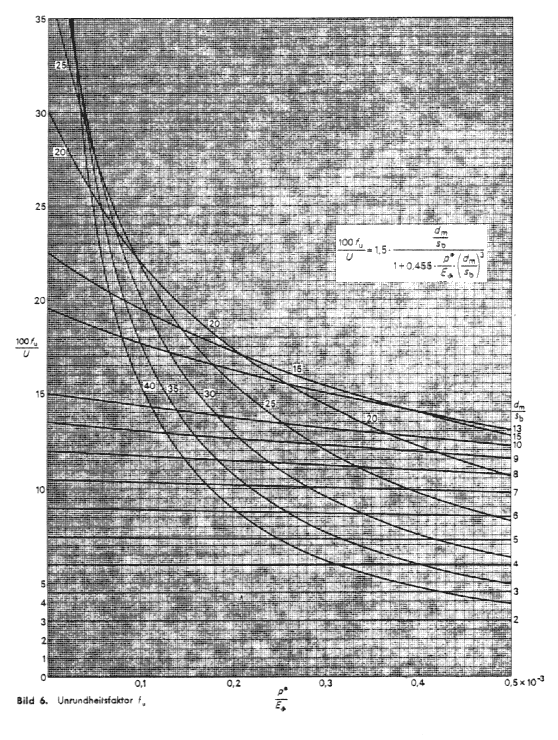
(3) Unrundheitsfaktor fu für elliptische Formabweichung. Bild 6,
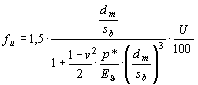 (5)
(5)
 |  |
 |  |
 |  |
3.1.2. Zylinderschalen mit schrägen und/oder nicht radial angeordneten Abzweigen sind vorerst noch Nummer 3.1.1 zu berechnen.
3.1.3. Lochfelder in Zylinderscholen werden bei dieser Betrachtung wie Einzelausschnitte noch Nummer 3.1.1 behandelt.
3.1.4. Zylinderschalen mit Y-förmigen Abzweigen unter dem Öffnungswinkel ψA sind vorerst wie folgt zu berechnen:
σip = αm ⋅ p* dm/2sb (6)
Hierin ist einzusetzen:
αm = 2,5 + (90-ψA)2 / 1000 (7)
jedoch nicht weniger als 3,2.
Eine Schweißnahtwurzel im Zwickelbereich ist zu bearbeiten; falls dies nicht möglich ist, ist αm mit f4 = 1,2 zu multiplizieren.
3.2. Ideal-elastische Lochrand-Wärmespannungen
Diese Spannungen hängen nur vom radialen Temperaturverlauf in der Behälterwand ab. Für die Innenwand gilt unter der Annahme eines rotationssymmetrischen Temperaturverlaufs (auch bei Thermoschock)
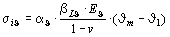 (8)
(8)
Hierin ist die Formzahl αϑ = 2 einzusetzen, es sei denn, daß ein anderer Wert rechnerisch nachgewiesen wird.
Unter der Voraussetzung eines quasistationären Temperaturverlaufs bei isolierter Außenwand wird die Temperaturdifferenz Δϑ = ϑm - ϑi = const. = Δϑ∞ und kann wie folgt als Funktion der Temperaturänderungsgeschwindigkeit vϑ angegeben werden:
Δϑ∞ = 1/aϑ ⋅ Φf ⋅ vϑ ⋅ sb2 (9)
Hier ist Φf ein Farmfaktor nach Bild 7.
Für die meßtechnische Überwachung kann ϑm mit ausreichender Genauigkeit in der Mitte der Wand gemessen werden.
4. Gesamtspannungszustand
Liegen außer Innendruck keine nennenswerten äußeren Kräfte und Momente vor, so laßt sich die Gesamt-Lochrandspannung wie folgt ermitteln:
σi = σip + σiϑ (10)
5. Zulässige Spannungen und Lastwechselzahlen
5.1. Spannungsgrenzen bei bekannter Lastwechselzahl
5.1.1. Ist nur die Anzahl n der vorgesehenen oder zu erwartenden Kaltstarts angegeben, so ist die Anriß-Lastwechselzahl Für die Lastwechselzahlen 5.1.2 Für ungekerbte Stäbe sind noch Bild 8 die zulässigen Schwingbreiten 2σa, in Abhängigkeit von der Anriß-Lastwechselzahl n zu bestimmen.
Diese müssen für Bauteile wegen Oberflächeneinflüssen reduziert werden.
Dies erfolgt durch den Korrekturfaktor f3 nach Tafel 1 und ergibt
Δσ* = 2σa/f3 (11)
Diese Schwingbreite Δσ* ist folgender Korrektur zu unterziehen,
(1) Im elastischen Falle Δσ* < 2 (2) Im überelastischen Falle Δσ* > 2 5.1.3. Sind die zulässigen reduzierten Schwingbreiten Δ σi für die einzelnen Lastzyklen ermittelt, so müssen die zulässigen Oberspannungen Da die Spannungsgrenzen für die einzelnen Zyklen durch die Wahl der An- und Abfahrgeschwindigkeit beeinflußbar sind, kann man sie in einem gewissen Bereich frei wählen.
Hier empfiehlt sich, γ > 0 ist das absolute Verhältnis der zulässigen Wärmespannung bei Abfahrbeginn zur zulässigen Wärmespannung bei Anfahrbeginn.
Wenn bei Abfahrbeginn nicht nur die Temperatur, sondern auch der Druck abgesenkt wird, das Bauteil dabei nicht regelmäßig durch zusätzlich eingeleitetes kälteres Medium gekühlt wird und zwischen Kesselhersteller, Besteller und Überwacher nichts anderes vereinbart wird, kann mit γ = 0 gerechnet werden.
In diesem Fall ist also Ansonsten wird die Oberspannung 5.1.4. Bei wasserberührten Teilen aus nicht austenitischen Stählen muß auf die Erhaltung der Magnetitschutzschicht besonders geachtet werden.
Für diese Teile werden daher die Spannungsgrenzen zusätzlich wie folgt eingeschränkt:
5.1.5. Die Gl. (14) bis (17) ergeben die zulässigen Ober- und Unterspannungen für die einzelnen Lastzyklen.
Aus diesen lassen sich mit den Gl. (8) und (10) die zulässigen Temperaturdifferenzen beim An- und Abfahren wie folgt berechnen:
Anfahren:
Abfahren:
5.2. Zulässige Lastwechselzahl für gegebene Spannungen
5.2.1. Sind für einen Lastzyklus die Spannungsgrenzen Ausgehend von der vorhandenen Spannungsschwingbreite
Δσi = gilt
(1) für den überelastischen Fall Δσi > 2 ⋅ σ0,2/ϑ *
(2) für den elastischen Fall Δσi < 2 ⋅ σ0,2/ϑ*
Mit dem Wert 2σa wird die Anriß-Lastwechselzahl Bild 8: Zulässige Spannungsschwingbreite 2σ a bei der maßgebenden Zyklustemperatur ϑ* in Abhängigkeitvon der Anrißlastzahl Die zulässige Lastwechselzahl ergibt sich hieraus für alleinige Kaltstarts zu n = Für Lastwechselkollektive sind die zulässigen Lastwechselzahlen n1, n2, n3, ..... so zu wählen, daß Gl. (25) erfüllt ist.
5.2.2. Für Vorausberechnungen können die Spannungsgrenzen Die Ergebnisse nach Gl. (23) und (24) liegen auf der sicheren Seite, weil die maximale Wärmespannung und die maximale mechanische Spannung ohne Berücksichtigung einer zusätzlichen Phasenverschiebung addiert werden.
Für genauere Berechnungen ist die tatsächliche zeitliche Zuordnung zu beachten.
5.2.3. Bei wasserberührten Teilen dürfen 6. Überlagerung verschiedener Lastzyklen
Ein gegebenes Laufwechselkollektiv mit nach Größe und Häufigkeit unregelmäßig schwankenden Spannungen wird in Lautzyklen gleicher oder nahezu gleicher Schwingbreite (wie z.B. Kalt- und Warmstarts) zerlegt und nach der linearen Schädigungsakkumulationshypothese bewertet.
Hiernach muß der Erschöpfungsgrad D aller Lautzyklen beschränkt bleiben auf
Erschöpfungssicherheit SD > 2
Tafel 1. Korrekturfaktor f3 zur Berücksichtigung des Oberflächeneinflusses in Abhängigkeit von der Streckgrenze
1) Erläuterungen in Vorbereitung
2) Der Faktor 1,15 entspricht etwa der halben Plustoleranz von 25 % für Rohre mit Mindestwanddicke
3) Stoffwerte sind VDI-Richtlinie 3128
Formblatt 1: Formblatt zur Berechnung der zulässigen Lastwechselzahl bei vorgegebenen Temperaturdifferenzen bzw. Temperaturänderungsgescbwindigkeiten
a) Konstruktions- und Bererchnungsdaten b) Rechenschema Lastkollektiv: ni wählen; *) Siehe hierzu die Bemerkungen unter Abschnitt 5.2.2 der Anlage 1 zur TRD 301 Formblatt 2: Formblatt zur Berechnung der zulässigen Temperaturdifferenzen und Temperaturänderungsgeschwindigkeiten bei vorgegebener Lastwechselzahl
b) Rechenschema N/mm2 N/mm2 Grapische Darstellung der Ergebnisse: 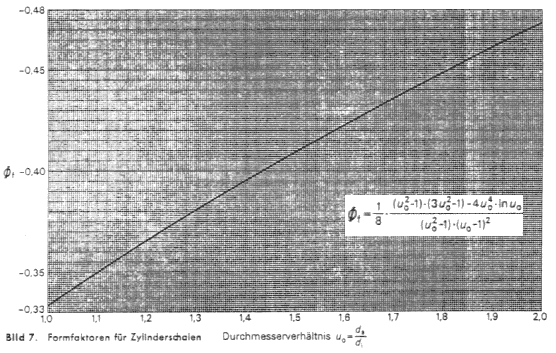
 > 5 ⋅ n zugrunde zu legen, damit genügende Reserven für Warmstarts sichergestellt werden (siehe TRD 301 Nummer 6.2.1). Ist dagegen ein Lastwechselkollektiv, bestehend aus n1 Kaltstarts und n2, n3, ... Warmstarts (mit gegebenenfalls unterschiedlichsten Anfangs- und Endzuständen) gegeben, so sind die Anriß-Lastwechselzahlen
> 5 ⋅ n zugrunde zu legen, damit genügende Reserven für Warmstarts sichergestellt werden (siehe TRD 301 Nummer 6.2.1). Ist dagegen ein Lastwechselkollektiv, bestehend aus n1 Kaltstarts und n2, n3, ... Warmstarts (mit gegebenenfalls unterschiedlichsten Anfangs- und Endzuständen) gegeben, so sind die Anriß-Lastwechselzahlen  1,
1,  2,
2,  3
usw. so zu wählen, daß Gl. (25) erfüllt wird.
3
usw. so zu wählen, daß Gl. (25) erfüllt wird.
 1,
1,  2 usw. müssen nach Nummer 5.1.2 die reduzierten Schwingbreiten ermittelt werden.
2 usw. müssen nach Nummer 5.1.2 die reduzierten Schwingbreiten ermittelt werden.
 0,2/ϑ* ist eine Korrektur erforderlich, um den Einfluß der größtmöglichen Mittelspannung zu berücksichtigen.
Man erhält unter Verwendung der Gerber-Parabel die zulässige reduzierte Schwingbreite der ideal-elastischen Spannungen
0,2/ϑ* ist eine Korrektur erforderlich, um den Einfluß der größtmöglichen Mittelspannung zu berücksichtigen.
Man erhält unter Verwendung der Gerber-Parabel die zulässige reduzierte Schwingbreite der ideal-elastischen Spannungen
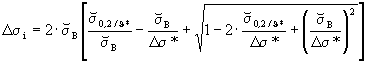 (12)
(12)
 0,2/ϑ* ist zu berücksichtigen, daß man in Wirklichkeit mit einer größeren Dehnung als der im idealisierten elastischen Fall rechnen muß. Es gilt dann
0,2/ϑ* ist zu berücksichtigen, daß man in Wirklichkeit mit einer größeren Dehnung als der im idealisierten elastischen Fall rechnen muß. Es gilt dann
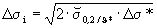 (13)
(13)
 i, und die zulässigen Unterspannungen
i, und die zulässigen Unterspannungen  i, festgelegt werden, mit denen σi während des An- und Abfahrens zu begrenzen ist und schließlich die zulässigen Temperaturdifferenzen zu berechnen sind.
i, festgelegt werden, mit denen σi während des An- und Abfahrens zu begrenzen ist und schließlich die zulässigen Temperaturdifferenzen zu berechnen sind.
 i, über einen Beiwert γ wie folgt festzulegen:
i, über einen Beiwert γ wie folgt festzulegen:
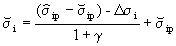 (14)
(14)
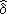 i =
i = 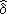 ip und
ip und 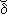 i =
i = 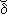 ip - Δδi.
ip - Δδi.
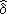 i =
i = 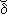 i - Δδi. (15).
i - Δδi. (15).
 i
> σip4 - 600 N/mm2 (16)
i
> σip4 - 600 N/mm2 (16)
 i < σip4 + 200 N/mm2 (17)
i < σip4 + 200 N/mm2 (17)
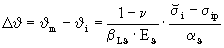 (18)
(18)
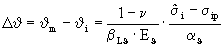 (19)
(19)
 1, und
1, und  1 bekannt, so läßt sich die Anriß-Lastwechselzahl
1 bekannt, so läßt sich die Anriß-Lastwechselzahl  für diesen Zyklus wie folgt ermitteln:
für diesen Zyklus wie folgt ermitteln:
 i -
i -  i (20)
i (20)
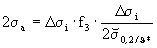 (21)
(21)
 (22)
(22)
 aus Bild 8 entnommen.
aus Bild 8 entnommen.
 für ungekerbte Probestäbe aus warmfesten ferritischen Walz- und Schmiedestäbe
für ungekerbte Probestäbe aus warmfesten ferritischen Walz- und Schmiedestäbe
(gilt vorerst auch für austenitische Stähle) (Nach Versuchen der MPA-Stuttgart an ungekerbten Stäben)

 /5.
/5.
 i und
i und  i ausgehend von den Temperaturänderungsgeschwindigkeiten vϑ1, und vϑ2 unter der Annahme quasistationärer Verhältnisse, wie folgt abgeschätzt werden:
i ausgehend von den Temperaturänderungsgeschwindigkeiten vϑ1, und vϑ2 unter der Annahme quasistationärer Verhältnisse, wie folgt abgeschätzt werden:
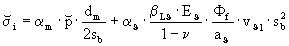 (23)
(23)
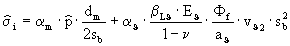 (24)
(24)
 i und
i und  i die unter Nummer 5.1.4 festgelegten Grenzen nicht überschreiten, was gegebenenfalls durch Begrenzung der ideal-elastischen Wärmespannungen zu erzielen ist.
i die unter Nummer 5.1.4 festgelegten Grenzen nicht überschreiten, was gegebenenfalls durch Begrenzung der ideal-elastischen Wärmespannungen zu erzielen ist.
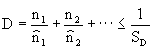 (25)
(25)
σ s in N/mm2 f3 < 355 1,0 > 355 bis 600 1,2 > 600 1,4
1 Art und (Nenn-)Abmessungen der Kugelschale 2 Werkstoff nahtlos
längsgschweißt3 Berechnungswanddicke
(ohne Wärmespannung: sb = sv)sb = (gemessen)
sb = × 1,15 (gepreßt)
sb = + l (längsgeschweißt)sb mm 4 innerer Durchmesser (bei äußerem Ø di= da - 2⋅ sb) di mm 5 größter Ausschnittdurchmesser dAi mm 6 Unrundheit U % 7 Öffnungswinkel für Y-förmige Abzweige ψA ° 8 Betriebsüberdruck p4 N/mm2 9 minimaler Zyklusdruck (für Kaltstart  = 0)
= 0)
N/mm2 10 maximaler Zyklusdruck 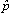
N/mm2 11 minimale Zyklustemperatur 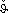
°C 12 maximale Zyklustemperatur 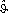
°C 13 maßgebende Zyklustemperatur ϑ* = 0,75 · 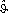 + 0,25 ·
+ 0,25 ·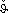
ϑ* °C 14 Anfahrgeschwindigkeit bei Anfahrbeginn, quasistationär gerechnet bei  (positiv)
(positiv)vv1 K/min 15 Temperaturdifferenz bei Anfahrbeginn, bei  (negativ!)
(negativ!)Δv1 K 16 Abfahrgeschwindigkeit bei Abfahrbeginn, quasistationär gerechnet bei 
(für γ = 0 wird vv2= 0, sonst negativ)vv2 K/min 17 Temperaturdifferenz bei Abfahrbeginn bei 
(für γ = 0 wird Δv2 = 0, sonst positiv!)Δv2 K 18 differentieller Wärmeausdehnungskoeffizient (bei ϑ*) βLϑ 1/K 19 Temperaturleitfähigkeit (bei ϑ*) aϑ mm2/min 20 (Mindest-) Zugfestigkeit (bei Raumtemperatur)  B
BN/mm2 21
Faktor f3 ⌈
{
⌊= 1,0 (wenn  s < 355 N/mm2)
s < 355 N/mm2)
= 1,2 (355 <  s < 600 N/mm2)
s < 600 N/mm2)
= 1,4 (wenn  s > 600 N/mm2)
s > 600 N/mm2)f3 - 22 theoretische Formzahl
für Membranspannungαm0 = 2,6 geschmiedet/durchgesteckt
αm0 = 2,9 aufgeschweißt ohne Spalt
αm0 = 3,2 ausgehalstαm0 - 23
Faktor f4 ⌈
{
⌊ = 1,0 (bearbeitete Wurzeln)
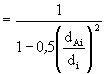 (unbearbeitet)
(unbearbeitet)
= 1,2 Y-Abzweig (unbearbeitet)f4 -
24 dm = 0,5(da + di) dm mm 25 u0 = 1 + 2 (sb / di) u0 - 26 W = 0,35 / (βLϑ · Eϑ) W (mm2·K)/N 27 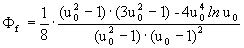
aus Diagramm entnehmen
oder maschinell rechnenΦf - 28 V= aϑ /(Φf
⋅ sb2 V 1/min 29 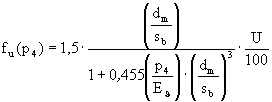
fu(p4) - 30 αm(p4) = αm0 · f4 + 2 · fu(p4) oder 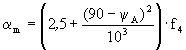
αm > 3,2αm(p4) - 31 αip4 = αm0(p4) · p4 · dm/2sb σ ip4 N/mm2 32 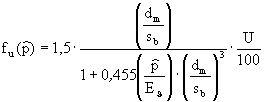
fu( 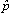 )
)- 33 αm( 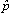 ) = αm0 · f4 + 2 · fu(
) = αm0 · f4 + 2 · fu(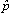 ) oder
) oder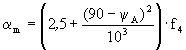
αm > 3,2αm( 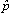 )
)- 34  ip = αm(
ip = αm(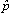 ) ·
) · 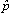 · dm/2sb
· dm/2sb ip
ipN/mm2 35 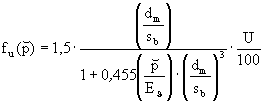
fu(  )
)- 36 αm(  ) = αm0 · f4 + 2 · fu(
) = αm0 · f4 + 2 · fu( ) oder
) oder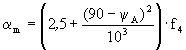
αm > 3,2αm(  )
)- 37  ip = αm(
ip = αm( ) ·
) ·  · dm/2sb
· dm/2sb ip
ipN/mm2 38 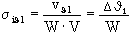
σiϑ1 N/mm2 39 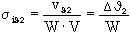
σiϑ2 N/mm2 40  i =
i =  ip + σiϑ1 * (quasistationärer Fall !)
ip + σiϑ1 * (quasistationärer Fall !) i
iN/mm2 41  i =
i =  ip + σiϑ2 * (quasistationärer Fall !)
ip + σiϑ2 * (quasistationärer Fall !) i
iN/mm2 42 Δσi =  i -
i -  i
i Δσi N/mm2 43
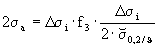
wenn Δσi > 2 ⋅  0,2/ϑ
0,2/ϑ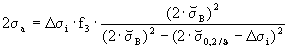
(bei Abfahrbeginn und γ = 0 wird δiv2 = 0)wenn Δσi < 2 ⋅  0,2/ϑ
0,2/ϑ2σa N/mm2 44 Anriß-Lastwechselzahl  für 2σa bei ϑ*
für 2σa bei ϑ*
- 45 zulässige Anzahl der Zyklen nur Kaltstart: n < (  /5)
/5)
Σ(ni/ i) < 0,5
i) < 0,5n - 46 S1 = σip4 - 600 S1 N/mm2 47 S2 = σip4 + 200 S2 N/mm2 48 Bei wasserbenetzten Teilen müssen noch zusätzlich erfüllt sein:
S1 <  i S2
>
i S2
>  i
i
1 Art und (Nenn-)Abmessungen der Kugelschale 2 Werkstoff nahtlos längsgeschweißt 3 Berechnungswanddicke: sb = (gemessen)
sb = × 1,15 (nahtlos)
sb = + 1 (längsgeschweißt)sb mm 4 innerer Durchmesser (bei äußerem Ø di = da - 2 ⋅Sb) di mm 5 größter Ausschnittdurchmesser dAi mm 6 Öffnungswinkel für Y-förmige Abzweige ψ A ° 7 Betriebsüberdruck p4 N/mm2 8 minimaler Zyklusdruck (für Kaltstart  = 0)
= 0) 
N/mm2 9 maximaler Zyklusdruck 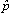
N/mm2 10 minimale Zyklustemperatur 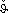
°C 11 maximale Zyklustemperatur 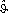
°C 12 geforderte Lastwechselzahl (für Kaltstart n > 2000) n - 13 Anriß-Lastspielzahl nur Kaltstart:  > 5 ⋅ n
> 5 ⋅ n
Lastkollektiv: ni wählen: Σ(ni/ )
< 0,5
)
< 0,5
- 14 maßgeb. Zyklustemperatur ϑ* = 0,75 ⋅ 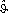 + 0,25 ⋅
+ 0,25 ⋅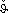
ϑ* °C 15 Elastizitätsmodul (bei ϑ*) Εϑ N/mm2 16 (Mindest-)Warmstreckgrenze (bei ϑ*)  0,2/ϑ
0,2/ϑN/mm2 17 differentieller Wärmeausdehnungskoeffizient (bei ϑ*) βLϑ 1/K 18 Temperaturleitfähigkeit (bei ϑ*) aϑ mm2/min 19 (Mindest-)Zugfestigkeit (bei Raumtemperatur)  B
BN/mm2 20 Verhältniszahl γ γ = 1 (Normalfall)
0 < γ < 1 (für schnelleres Anfahren)
γ > 1 (für schnelleres Abfahren)γ - 21
Faktor f3 ⌈
{
⌊= 1,0 (wenn  s < 355 N/mm2)
s < 355 N/mm2)
= 1,2 (355 <  s < 600 N/mm2)
s < 600 N/mm2)
= 1,4 (wenn  s > 600 N/mm2)
s > 600 N/mm2)f3 - 22 Zulässige Schwingbreite (2σa für  bei ϑ*)
bei ϑ*)2σa N/mm2 23. Unrundheit U % 24 theoretische Formzahl
für Membranspannungαm0 = 2,6 geschmiedet/durchgesteckt
αm0 = 2,9 aufgeschweißt ohne Spalt
αm0 = 3,2 ausgehalstαm0 - 25
Faktor f4 ⌈
{
⌊ = 1,0 (bearbeitete Wurzeln)
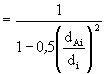 (unbearbeitet)
(unbearbeitet)
= 1,2 Y-Abzweig (unbearbeitet)f4 -
26 dm = 0,5(da + di) dm mm 27 u0 = 1 + 2 (sb / di) = u0 - 28 W = 0,35 / (βLϑ · Eϑ) W mm2·K / N 29 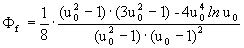
aus Diagramm entnehmen
oder maschinell rechnenΦf - 30 V = aϑ / (Φf ⋅ sb2) V 1/min 31 Δσ* = 2 σa / f3 Δσzul N/mm2 32 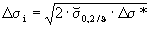 (für den überelastischen Fall Δσ*
> 2 ⋅
(für den überelastischen Fall Δσ*
> 2 ⋅ 0,2/ϑ)
0,2/ϑ)
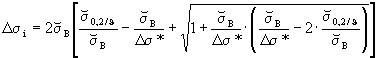
(für den elastischen Fall)Δσi N/mm2 33 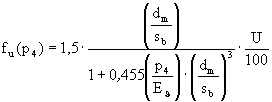
fu(p4) - 34 αm(p4) = αm0 · f4 + 2 · fu(p4) oder 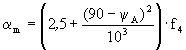
αm > 3,2αm(p4) - 35 σip4 = αm0(p4) · p4 · dm/2sb σip4 N/mm2 36 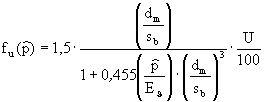
fu( 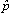 )
)- 37 αm( 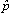 ) = αm0 · f4 + 2 · fu(
) = αm0 · f4 + 2 · fu(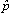 ) oder
) oder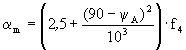
αm > 3,2αm( 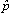 )
)- 38  ip = αm(
ip = αm(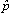 ) ·
) · 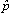 · dm/2sb
· dm/2sb ip
ipN/mm2 39 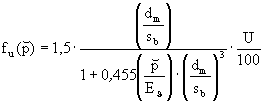
fu(  )
)- 40 αm(  ) = αm0 · f4 + 2 · fu(
) = αm0 · f4 + 2 · fu( ) oder
) oder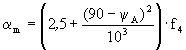
αm > 3,2αm(  )
)- 41  ip = αm(
ip = αm( ) ·
) ·  · dm/2sb
· dm/2sb ip
ipN/mm2 42 S1 =  ip/ (1+γ) +
ip/ (1+γ) + -
-  ip - Δσi
ip - ΔσiS1 N/mm2 43 S2 = σip4 - 600 S2 N/mm2 44  i = S1
i = S1
 i = S2
i = S2
 i = S1
i = S1(nicht wasserbenetzt)
wenn S2 > S1 (bei Wasserbenetzung)
wenn S1 > S2 (bei Wasserbenetzung)
 i
i
45 S3 = Δσ i +  i
iS3 N/mm2 46 S4 = σip4 + 200 S4 N/mm2 47  i = S3
i = S3
 i = S4
i = S4
 i = S3
i = S3(nicht wasserbenetzt)
wenn S4 < S3 (bei Wasserbenetzung)
wenn S3 < S4 (bei Wasserbenetzung)
 i
i
48 Δϑ1 = W ⋅ (  i -
i -  ip)
ip) Δϑ1 K 49 Δϑ2 = W ⋅ (  i -
i -  ip)
ip) Δϑ2 K 50 Δϑ3 = W ⋅ (  i -
i -  ip)
ip) Δϑ3 K 51 Δϑ4 = W ⋅ (  i -
i -  ip)
ip) Δϑ4 K 52 vϑ1 = V ⋅ Δϑ1 * vϑ1 K/min 53 vϑ2 = V ⋅ Δϑ2 * vϑ2 K/min 54 vϑ 3 = V ×Δϑ3 * vϑ3 K/min 55 vϑ4 = V ⋅ Δϑ4 * vϑ4 K/min * Siehe hierzu die Bemerkung unter Nummer 5.2.2 der Anlage
Bild 1 Zulässige Temperaturdifferenzen
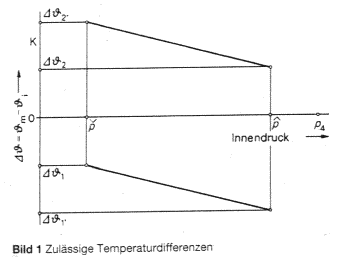
Bild 2 Zulässige Temperaturänderungsgeschwindigkeit, quasistationär gerechnet
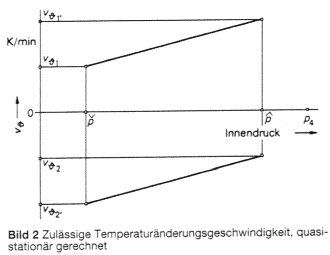

ENDE 