| 1 | Art und (Nenn-)Abmessungen der Kugelschale |
| 2 | Werkstoff | Herstellungsverfahren (gepreßt/gedreht) |
| 3 | Berechnungswanddicke: | Sb = (gemessen)
Sb = Se ⋅ 1,15 (gepreßt)
Sb = Se ⋅ 1,05, Sb < Se + 1 mm
(Böden nach DIN)
Sb = Se (gedreht) | Sb | mm |
| 4 | innerer Durchmesser (bei äußerem Ø di = da - 2 ⋅ Sb) | di | mm |
| 5 | größter Ausschnittdurchmesser | dAi | mm |
| 6 | Verhältnis der Halhachsen bei elliptischen Ausschnitten | αψ | - |
| 7 | Betriebsüberdruck | p4 | N/mm2 |
| 8 | minimaler Zyklusdruck | (für Kaltstart  = 0) = 0) |  | N/mm2 |
| 9 | maximaler Zyklusdruck | 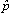 | N/mm2 |
| 10 | minimale Zyklustemperatur | 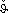 | °C |
| 11 | maximale Zyklustemperatur | 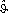 | °C |
| 12 | geforderte Lastwechselzahl | (für Kaltstart n > 2000) | n | °C |
| 13 | Anriß-Lastspielzahl | nur Kaltstart:  > 5 n > 5 n
Lastkollektiv: ni wählen: Σ(ni/ )
< 0,5 )
< 0,5 |  | - |
| 14 | maßgeb. Zyklustemperatur | ϑ* = 0,75 ⋅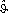 + 0,25 ⋅ + 0,25 ⋅ 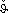 | ϑ* | |
| 15 | Elastizitätsmodul | (bei ϑ*) | Εϑ | N/mm2 |
| 16 | (Mindest-)Warmstreckgrenze | (bei ϑ*) |  0,2/ϑ 0,2/ϑ | N/mm2 |
| 17 | differentieller Wärmeausdehnungskoeffizient | (bei ϑ*) | βLϑ | 1/K |
| 18 | Temperaturleitfähigkeit | (bei ϑ*) | aϑ | mm2/min |
| 19 | (Mindest-)Zugfestigkeit | (bei Raumtemperatur) |  B B | N/mm2 |
| 20 | Verhältniszahl γ (s. TRD 301 Anlage 1, Abschnitt 5.1.3) |
| 21 | | = 1,0 (wenn  s < 355 N/mm2) s < 355 N/mm2)
= 1,2 (355 <  s < 600 N/mm2) s < 600 N/mm2)
= 1,4 (wenn  s >600 N/mm2) s >600 N/mm2) | f3 | - |
| 22 | Zulässige Schwingbreite | (2 σ a für  bei ϑ*) bei ϑ*) | 2σa | N/mm2 |
| 23. | u0 = l + 2 ⋅ sb/di | u0 | - |
| 24 | 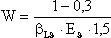 | W | (mm2⋅K)/ N |
| 25 | 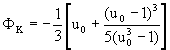 | aus Diagramm entnehmen
oder maschinell rechnen | ΦK | - |
| 26 | V = aϑ / (Φ K ⋅ sb2) | V | 1/min |
| 27 | Δσ * = 2σa / f3 | Δσzul | N/mm2 |
| 28 | 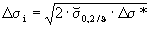 (für den überelastischen Fall Δσ* > 2 ⋅ (für den überelastischen Fall Δσ* > 2 ⋅ 0,2/ϑ 0,2/ϑ
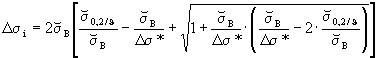
(für den elastischen Fall Δσ* < 2 ⋅ 0,2/ϑ) 0,2/ϑ)
| Δσi | N/mm2 |
| 29 | Formfaktor Lochrand
α m = 2,0 für nicht drucktragende, durchgesteckte Stutzen
α m = 2,5 für aufgesetzte und durchgesteckte Stutzen, wenn sb/di > 0,04 ist
α m = 2,9 bei anderen Bauarten und wenn sb/di <0,04 ist | αm | - |
| 30 |
| αψ = | ⌈
{
⌊ | 1 bei radialen Abzweigen,
Verhältnis große Halbachse/kleine Halbachse bei elliptischen Ausschnitten
und bei schrägen Stutzen |
| αψ | - |
| 31 | H = α m ⋅ α ψ ⋅ dm/(4 ⋅ sb) | H | - |
| 32 | s ip4 = H ⋅ p4 | σip4 | N/mm2 |
| 33 |  ip = H ⋅ ip = H ⋅ 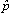 |  ip ip | N/mm2 |
| 34 |  ip = H ⋅ ip = H ⋅  |  ip ip | N/mm2 |
| 35 | 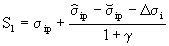 | S1 | N/mm2 |
| 36 | S2 = σ ip4 - 600 | S2 | N/mm2 |
| 37 |  i = S1 i = S1
 i = S2 i = S2
 i = S1 i = S1 | (nicht wasserberührt)
wenn S2 > S1 (wasserberührt)
wenn S1 > S2 (wasserberührt) |  i i | N/mm2 |
| 38 | S3 = Δσ i +  i i | S3 | N/mm2 |
| 39 | S4 = σ ip4 + 200 | S4 | N/mm2 |
| 40 |  i = S3 i = S3
 i = S4 i = S4
 i = S3 i = S3 | (nicht wasserberührt)
wenn S4 < S3 (wasserberührt)
wenn S3 < S4 (wasserberührt) |  i i | N/mm2 |
| 41 | Δϑ 1 = W ⋅ ( i - i -  ip) ip) | Δϑ1 | K |
| 42 | Δϑ 1 = W ⋅ ( i - i -  ip) ip) | Δϑ1' | K |
| 43 | Δϑ 2 = W ⋅ ( i - i -  ip) ip) | Δϑ2 | K |
| 44 | Δϑ 2 = W ⋅ ( i - i -  ip) ip) | Δϑ2' | K |
| 45 | vϑ 1 = V ⋅ Δϑ1 | vϑ1 | K/min |
| 46 | vϑ1' = V ⋅ Δϑ1' | vϑ1' | K/min |
| 47 | vϑ 2 = V ⋅ Δϑ 2 | vϑ 2 | K/mm |
| 48 | vϑ2' = V ⋅ Δϑ2' | vϑ2' | K/mm |
 = 0)
= 0) 
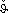
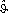
 > 5 n
> 5 n )
< 0,5
)
< 0,5 
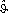 + 0,25 ⋅
+ 0,25 ⋅ 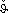
 0,2/ϑ
0,2/ϑ B
B s < 355 N/mm2)
s < 355 N/mm2) s < 600 N/mm2)
s < 600 N/mm2) s >600 N/mm2)
s >600 N/mm2) bei ϑ*)
bei ϑ*)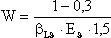
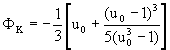
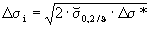 (für den überelastischen Fall Δσ* > 2 ⋅
(für den überelastischen Fall Δσ* > 2 ⋅ 0,2/ϑ
0,2/ϑ
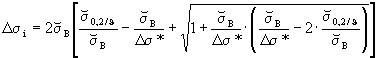
 0,2/ϑ)
0,2/ϑ)  ip = H ⋅
ip = H ⋅ 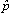
 ip
ip ip = H ⋅
ip = H ⋅ 
 ip
ip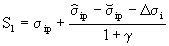
 i = S1
i = S1 i = S2
i = S2 i = S1
i = S1 i
i i
i i = S3
i = S3 i = S4
i = S4 i = S3
i = S3 i
i i -
i -  ip)
ip)  i -
i -  ip)
ip)  i -
i -  ip)
ip)  i -
i -  ip)
ip)