

 |
zurück |  |
| Konfidenzgrenzen zum Erwartungswert normal und lognormal verteilter Zufallsgrößen | Anhang D |
D.1 Konzepte zur Beurteilung von Erwartungswerten anhand von Stichproben
Eine normalverteilte Zufallsgröße X ~ N(μ ;σ ) hat die Verteilungsfunktion
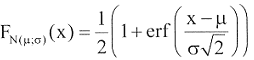 |
(D1) |
und den Erwartungswert
| E = μ . | (D2) |
Eine lognormal verteilte Zufallsgröße Y ~ Ln(μ ;σ ) hat die Verteilungsfunktion
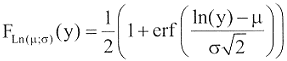 |
(D3) |
und den Erwartungswert
| E = exp (μ + σ2/2) | (D4) |
In der Praxis können für die Erwartungswerte (D2) bzw. (D4) jedoch nur Schätzungen auf der Basis von Stichproben (Messwerten) vorgenommen werden. Die in Anhang C erläuterten Methoden zur Schätzung der Verteilungsparameter μ und σ sind dafür eine wesentliche Basis.
Nachfolgend wird angenommen, dass mögliche Störungen der Normal- bzw. Lognormalverteilung durch Ausreißer (oder Störungen der Lognormalverteilung durch einen konstanten Untergrund c) bereits separiert wurden. Hier werden deshalb nur Schätzungen zum Erwartungswert für "reine" normal bzw. lognormal verteilte Zufallsgrößen betrachtet.
Zur Beurteilung des Erwartungswertes einer Zufallsgröße anhand von Stichproben können im Prinzip zwei unterschiedliche Konzepte und entsprechende Kenngrößen genutzt werden. Sehr oft wird der Erwartungswert nur auf der Basis so genannter Punktschätzer En beurteilt. Der bekannteste Punktschätzer ist der arithmetische Mittelwert En(AM) der n Stichprobenwerte. Er hängt nicht von der Art der statistischen Verteilung ab. Für normal verteilte Zufallsgrößen stimmt er mit dem so genannten Maximum-Likelihood-Schätzer En(ML) überein, der sich für beide Verteilungsarten durch Einsetzen der Schätzwerte μn und σn der Verteilungsparameter in die Formeln (D2) bzw. (D4) ergibt (siehe [D1]):
| Normalverteilung: En(ML) = µn, | (D5) |
| Lognormalverteilung: En(ML) = exp (µn + σ2n/ 2). | (D6) |
Die Schätzwerte (D5) und (D6) sind ebenfalls Zufallsgrößen, da sie aus zufällig gewonnenen Stichprobenwerten resultieren. Sie liegen umso wahrscheinlicher in der Nähe des (wahren, aber immer unbekannten) Erwartungswertes E, je größer der Stichprobenumfang n ist. Die zufälligen Abweichungen der Schätzwerte En vom wahren Erwartungswert E können besonders im Fall der Lognormalverteilung (D3) bei größeren Werten von σ so groß sein, dass die auf der Grundlage von Punktschätzern getroffenen Aussagen den realen Gegebenheiten nicht mehr gerecht werden [D2].
Will man anhand von Stichproben mit einer bestimmten Sicherheit beurteilen, wie groß der wahre Wert von E sein könnte, so ist das Konzept der Konfidenzgrenzen zu verwenden, mit dem für E eine "Intervallschätzung" vorgenommen wird. Hierbei wird eine obere Konfidenzgrenze bestimmt, die mit einer vorzugebenden Wahrscheinlichkeit P (dem Vertrauensniveau) größer als E ist, bzw. eine untere Konfidenzgrenze, die mit der Wahrscheinlichkeit P kleiner als E ist. Im Umweltschutz wird ein Vertrauensniveau von P = 0,95 i. Allg. als ausreichend sicher angesehen und hier nachfolgend als "vorgegeben" betrachtet.
In Abschnitt D.2 wird auf die Berechnung von Konfidenzgrenzen zum Erwartungswert von normal verteilten Zufallsgrößen eingegangen. In Abschnitt D.3 werden die zur Berechnung von Konfidenzgrenzen für den Erwartungswert von lognormal verteilten Zufallsgrößen benötigten Beziehungen erläutert. Eine detailliertere Darstellung und mathematische Ableitung dieser Beziehungen ist in [D2) enthalten. Zur Theorie der Konfidenzgrenzen linearer Funktionen des Er-wartungswertes und der Varianz von normal verteilten Zufallsgrößen sei auf [D3] hingewiesen.
Tabelle D1: Perzentile tn-1;P der t-Verteilung für Stichprobenumfänge n von 6 bis 100 für P = 0,95
| n | tn-1;P | n | tn-1;P | n | tn-1;P | n | tn-1;P | n | tn-1;P |
| 6 | 2,0150 | 25 | 1,7109 | 44 | 1,6811 | 63 | 1,6698 | 82 | 1,6639 |
| 7 | 1,9432 | 26 | 1,7081 | 45 | 1,6802 | 64 | 1,6694 | 83 | 1,6636 |
| 8 | 1,8946 | 27 | 1,7056 | 46 | 1,6794 | 65 | 1,6690 | 84 | 1,6634 |
| 9 | 1,8595 | 28 | 1,7033 | 47 | 1,6787 | 66 |
(Stand: 16.06.2018)
Alle vollständigen Texte in der aktuellen Fassung im Jahresabonnement
Nutzungsgebühr: 90.- € netto (Grundlizenz)
(derzeit ca. 7200 Titel s.Übersicht - keine Unterteilung in Fachbereiche)
Die Zugangskennung wird kurzfristig übermittelt
? Fragen ?
Abonnentenzugang/Volltextversion
...
X
⍂
↑
↓