zurück

E.2 Verbesserung der Repräsentativität durch einen erhöhten Stichprobenumfang oder durch die Verwendung von Mischproben

E.2.1 Erhöhung des Stichprobenumfangs

Für die in Abschnitt E.1.1 betrachtete Stichprobe {y}₂₀ergab sich, dass die Überwachungsgrenze von C = 1 mit der berechneten oberen Konfidenzgrenze von UL = E^(n;P)= 1,929 nicht nachgewiesen wurde. Dies dürfte aber mit großer Wahrscheinlichkeit daran liegen, dass der Stichprobenumfang (n = 20) für die Grundgesamtheit zu klein war. Der in die Berechnung der oberen Konfidenzgrenze eingehende Konfidenzfaktor hatte einen Wert von B(n = 20; P = 0,95; σ_n = 1,359) ≅ 2,65. Er bringt zum Ausdruck, dass die Schätzung des Erwartungswertes der untersuchten Grundgesamtheit mit der Stichprobe {y}₂₀ eine erhebliche statistische Unsicherheit aufweist.

Nimmt man an, dass die Schätzwerte μ_n und σ_n und damit auch E_n^(ML) den wahren Werten der Grundgesamtheit in etwa entsprechen, so kann man anhand der Abbildung Dia prognostizieren, in welchem Maße der Stichprobenumfang zum Nachweis der Einhaltung der Überwachungsgrenze C vergrößert werden sollte. Hierzu wäre eine Reduzierung des Konfidenzfaktors von 2,65 (s. o.) auf einen Wert von C/E_n^(ML)= 1/0,727 ≅ 1,38 nötig. Nach Abbildung Dia wird dazu mit σ_n zwischen 1,3 und 1,4 ein Stichprobenumfang von n ≈ 100 prognostiziert. Die genauere Berechnung des Konfidenzfaktors mit der analytischen Näherung aus Abschnitt D.2 ergibt: B(n = 100; P = 0,95; σ_n = 1,36) ≅ 1,42.

Für die Grundgesamtheit (E1) wurden dementsprechend 80 weitere zufällige Werte simuliert. Die zusammen mit den 20 Werten von Tabelle E1 resultierende Stichprobe {y}₁₀₀ enthält Tabelle E5. Der Q-Q-Plot dieser 100 Daten ist in Abbildung E8 dargestellt.

Zur vereinfachten Schätzung der oberen Konfidenzgrenze UL_r resultiert nach Gl. (12) die Prüfgröße

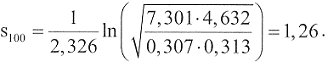
Gemäß Tabelle 3 und Gl. (13) ist y_<83> = 1,199 ein einfacher Schätzer zur oberen Konfidenzgrenze UL des Erwartungswertes. Da mit diesem Wert die relevante Überwachungsgrenze überschritten wird, ist eine genauere Berechnung der oberen Konfidenzgrenze erforderlich.

In Tabelle E6 sind die zur Stichprobe {y}₁₀₀ aus Tabelle E5 berechneten statistischen Kenngrößen zusammengestellt. Hierzu ergeben sich folgende Feststellungen:

• Die Stichprobe enthält keine Ausreißer und keinen konstanten Untergrund.
• Die Parameterwerte μ und σ der Verteilung (E1) wurden erneut relativ gut bestimmt, wobei der Vergleich mit Tabelle E2 zeigt, dass der Parameter p noch etwas stärker überschätzt und der Parameter a noch etwas stärker unterschätzt wurde als mit der Stichprobe {y}₂₀. Während sich der ML-Schätzwert E_n^(ML) geringfügig verkleinert hat, liegt der arithmetische Mittelwert jetzt deutlich näher am wahren Erwartungswert.
• Der Erwartungswert ist zum Vertrauensniveau P = 0,95 kleiner als 0,978 (und größer als 0,531). Dementsprechend würde man im Ergebnis der Erhöhung des Stichprobenumfangs auf n = 100 darauf schließen, dass auf Basis der oberen Konfidenzgrenze der Schätzung des Erwartungswertes von UL = E^(n;P) ≅ 0,98 die Einhaltung der Überwachungsgrenze von C = 1 mit einem Vertrauensniveau von P = 0,95 nachgewiesen wurde.

Tabelle E5: Einzelwerte y der zufälligen Stichprobe {y}₁₀₀ der Lognormalverteilung (E1); die 20 Werte der ursprünglichen Stichprobe {y}₂₀ aus Tabelle E1 sind fett markiert