 Für einen individuellen Ausdruck passen Sie bitte die
Für einen individuellen Ausdruck passen Sie bitte dieEinstellungen in der Druckvorschau Ihres Browsers an. Regelwerk

 Für einen individuellen Ausdruck passen Sie bitte die Für einen individuellen Ausdruck passen Sie bitte dieEinstellungen in der Druckvorschau Ihres Browsers an. Regelwerk |
 |
BUF - Berechnungsmethode für den Umgebungslärm von Flugplätzen
Vom 20. November 2018
(BAnz AT 28.12.2018 B7, 05.10.2021 B4aufgehoben)
(Anlage 2 zu BAnz AT 28.12.2018 B7)
1 Verwendete Begriffe und Symbole
Im folgenden Abschnitt werden häufig verwendete Begriffe und Symbole erläutert. Die Begriffe "Schall" und "Lärm" werden im Text synonym verwendet werden.
1.1 Begriffe
ANP-Datenbank
Datenbank der Lärm- und Leistungsdaten der Luftfahrzeuge (Aircraft Noise and Performance Database), die von Eurocontrol gepflegt wird. Alle für die Lärmkartierung erforderlichen Daten der ANP-Datenbank stehen in der Datenbank für die Berechnungsmethode für den Umgebungslärm von Flugplätzen ( BUF-D).
Äquivalenter DauerschallpegelLpeq
Zehnfacher dekadischer Logarithmus des Verhältnisses des über die ZeitT gemittelten Schalldruckquadrats zum Quadrat des Bezugsschalldruckspo.
Bahnbezugspunkt PB
Ursprung des Streckenkoordinatensystemss
Basispegel eines Schallereignisses
Der aus den NPD-Tabellen ausgelesene Schallexpositionspegel oder Maximalpegel.
Bewerteter SchalldruckpegelLp
Zehnfacher dekadischer Logarithmus des Verhältnisses des quadrierten Effektivwertes des Schalldrucks bei einer gegebenen Frequenz- und Zeitbewertung zum Quadrat des Bezugsschalldruckspo. Die Frequenzbewertung (z.B. A) wird als Index des SchalldruckpegelsLp angegeben, z.B.LpA
Energieanteil F
Verhältnis der von einem Segment ausgehenden empfangenen Schallenergie zu der von einer unendlichen Flugbahn ausgehenden empfangenen Energie.
Flugbahn
Die Trajektorie eines Luftfahrzeugs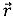 (s) im dreidimensionalen Raum
(s) im dreidimensionalen Raum
Flugbahnsegment
Teil einer Flugbahn, der durch eine gerade Linie endlicher Länge dargestellt wird
Flugbewegung
An- oder Abflug
FlughöheH (Altitude)
Höhe über Normalnull
Fluglärmkontur
Eine Linie eines konstanten Wertes eines Lärmindex um einen Flugplatz.
Flugparameter
Luftfahrzeugleistungseinstellung, -geschwindigkeit, -querneigung und -masse
Flugprofil
Verlauf der Flughöhez entlang des Kurses über Grund samt Änderungen derLuftfahrzeugkonfiguration, beschrieben durch eine Reihe vonProfilpunkten.
Flugstrecke
Festgelegte oder üblicherweise benutzte Streckenführung, die von Luftfahrzeugen eingehalten werden soll.
ANMERKUNG: Es werden Abflugstrecken, Anflugstrecken und Platzrunden unterschieden. Eine Flugstrecke wird in den Datenblättern zur Erfassung der Flugstreckenbeschreibungen durch Streckenabschnitte (Geraden, Kreisbögen) beschrieben.
Flugverfahren
Die Abfolge von Arbeitsschritten, die pilotenseitig ausgeführt werden: ausgedrückt als Änderungen der Luftfahrzeugkonfiguration in Abhängigkeit vom Abstand entlang des Kurses über Grund.
Geschwindigkeit über Grund
Geschwindigkeit eines Luftfahrzeugs bezogen auf einen festen Punkt am Boden.
Gewichteter äquivalenter SchallpegelLpeq,W
Eine modifizierte Version des äquivalenten DauerschallpegelsLpeq , bei der der Schall, der zu unterschiedlichen Tageszeiten auftritt, unterschiedlich gewichtet wird (in der Regel für Tag, Abend und Nacht).
Grundebene
Horizontale Bodenoberfläche durch den Flugplatzbezugspunkt, an dem die Konturen normalerweise berechnet werden.
Höhez (height)
Höhe über Grund. Vertikale Entfernung zwischen Luftfahrzeug undGrundebene.
Internationale Standardatmosphäre (ISA)
Definiert von der Internationalen Zivilluftfahrt-Organisation (ICAO). Definiert die Änderung von Lufttemperatur, -druck und -dichte in Abhängigkeit von der Höhe über Normalnull. Verwendet zur Normalisierung der Ergebnisse von Berechnungen zur Luftfahrzeugkonstruktion und Analyse von Testdaten.
Kernstrecke über Grund
Eine repräsentative oder nominelle Flugstrecke über Grund, die das Zentrum eines Korridors definiert.
Korrigierter Nettoschub
Bei einer gegebenen Leistungseinstellung (z.B. EPR oderN1) fällt der Nettoschub mit der Luftdichte und somit mit zunehmender Flughöhe; der korrigierte Nettoschub ist der Wert auf Meereshöhe.
Kumulativer Lärmpegel
Bezeichnet den zehnfachen dekadischen Logarithmus des Produkts von der logarithmischen Summe der vonNW Schallereignissen ausgehenden Schallexpositionspegel, die am jeweiligen Immissionsort während der ErhebungszeitTE im ZeitintervalltW auftreten und dem Quotienten(gW· to) / TE der ZeitgewichtungsfaktorengW , to undTE (z.B.LDay,LDEN).
Kurs über Grund
Vertikalprojektion der Flugbahn auf die Grundebene.
Lärm
Hörwahrnehmung, die zu Störungen, Belästigungen, Beeinträchtigungen oder Schäden führen kann.
Lärm- und Leistungsdaten eines Luftfahrzeugs
Daten, die die akustischen und leistungsbezogenen Werte verschiedener Luftfahrzeugmuster beschreiben, die für den Modellierungsprozess erforderlich sind. Dazu gehören dieLärm-Leistung-Abstand-Daten (NPD-Daten) und Angaben, die eine Berechnung des Triebwerkschubs in Abhängigkeit von derLuftfahrzeugkonfiguration ermöglichen. In der Regel werden diese Daten vom Luftfahrzeughersteller bereitgestellt, doch auch aus anderen Quellen gewonnen, wenn die erstgenannte Möglichkeit nicht besteht. Sind keine Daten verfügbar, werden zur Darstellung des betreffenden Luftfahrzeugs Daten eines lärm-äquivalenten Luftfahrzeugs verwendet; dies wird alsSubstitution bezeichnet.
Lärm-Leistung-Abstand-Daten (Noise-Power-Distance-Data, NPD-Daten)
Maximal- oder Schallexpositionspegel, tabellarisiert als Funktion derTriebwerksleistungseinstellung und des Abstands unter einem Luftfahrzeug im stationären Horizontalflug mit einer Bezugsgeschwindigkeit in einer Referenzatmosphäre. Mit den Daten wird dem Einfluss der Schalldämpfung aufgrund der Kugelwellenausbreitung (quadratisches Abstandsgesetz) und atmosphärischen Dämpfung Rechnung getragen. Der Abstand wird senkrecht zur Flugbahn des Luftfahrzeugs und zur Tragflächenachse bestimmt (d. h. vertikal unter dem Luftfahrzeug bei Flug ohne Schräglage). Die NPD-Daten sind der BUF-D zu entnehmen.
Lärmbezogener Leistungsparameter
Parameter, der die Vortriebswirkung angibt, die ein Triebwerk erzeugt, mit dem eine Emission von Schallleistung in Verbindung gebracht werden kann; in der Regel definiert alskorrigierter Nettoschub. Im gesamten Text verkürzt als "Leistung" oder "Leistungseinstellung" bezeichnet.
Lärmindex
Für den langfristigen oder kumulativen Schall ein Maß, das mit dessen Wirkung auf Menschen korreliert (d. h. als Indikator dafür angesehen wird); kann neben der Schallstärke zusätzliche Faktoren berücksichtigen (insbesondere die Tageszeit). Ein Beispiel ist der Tag-Abend-Nacht-PegelLDEN
Lärmsignifikanz
Der von einem Flugbahnsegment ausgehende Lärmanteil ist "lärmsignifikant", wenn er den Schallexpositionspegel in nennenswertem Umfang beeinflusst.
Lösen der Bremsen
sieheStart-of-Roll-Punkt
Luftfahrzeugbezugspunkt PF
Der Luftfahrzeugbezugspunkt PF bildet den Ursprung des Streckenkoordinatensystemss", auf das sich die Fixpunktprofile beziehen. PF ist bei Abflügen der Startpunkt, bei Anflügen die Landeschwelle und bei Hubschraubern die Hubschrauberstart- und -landestelle.
Luftfahrzeugkonfiguration
Die Positionen von Vorflügel, Landeklappen und Fahrwerk.
Maximaler Schalldruckpegel
Der höchste während eines Ereignisses erreichte Schalldruckpegel.
Nettoschub
Die von einem Triebwerk auf die Luftfahrzeugzelle ausgeübte Schubkraft.
Normalnull (NN)
Die Standardhöhenbezugsfläche, auf die sich dieISA bezieht.
Profilpunkt
Anfangs- oder Endpunkt eines Flugbahnsegments
Referenzatmosphäre
Eine tabellarische Zusammenstellung von Schallabsorptionsraten zur Vereinheitlichung der NPD-Daten.
Referenzdauer
Ein nomineller Zeitabschnitt, der zur Vereinheitlichung von Messungen des Schallexpositionspegels verwendet wird; die Referenzdauer beträgt eine Sekunde.
Referenzgeschwindigkeit
Geschwindigkeit über Grund eines Luftfahrzeugs, nach derSEL-Daten in den NPD-Tabellen normalisiert werden.
Referenztag
Bestimmte atmosphärische Bedingungen, nach denen die ANP-Daten vereinheitlich werden.
Schalldämpfung
Die Abnahme der Schallintensität mit der Entfernung entlang eines Ausbreitungsweges. Bei Fluglärm sind die Ursachen die Ausbreitung von Kugelwellen, die Luftabsorption und dieseitliche Dämpfung.
Schalldruckpegel
zehnfacher dekadischer Logarithmus des Verhältnisses des effektiven Schalldrucks zum Bezugswertpo jeweils im Quadrat. Empfangener Schall wird mit oder ohne "Frequenzbewertung" gemessen.
Schallexpositionspegel (SEL)LpAE
Zehnfacher dekadischer Logarithmus der SchallexpositionE zur BezugsschallexpositionEo. Dabei ist die Schallexposition E das Integral des zeitabhängigen Quadrates des frequenzbewerteten Schalldrucks über eine gegebene DauerT oder über ein Ereignis und die BezugsschallexpositionEo das Produkt aus dem Quadrat des Bezugsschalldruckspo und der Bezugsdauer von 1 s.
Schallintensität
Bezeichnet die Schallleistung, die je Flächeninhalt durch eine durchschallte Fläche tritt.
Seitliche Dämpfung
Zusätzliche, dem Vorhandensein der Bodenoberfläche direkt oder indirekt zurechenbare Dämpfung mit wachsendem Abstand. Erheblich bei niedrigen Höhenwinkeln des Luftfahrzeugs über der Grundebene.
SEL
Wird im Text alsSchallexpositionspegel LpAE bezeichnet.
ANMERKUNG: In den NPD-Tabellen wird SEL verwendet.
Start-of-Roll-Punkt (SOR)
Der Punkt auf der Startbahn, an dem ein abfliegendes Luftfahrzeug startet. Auch bezeichnet als "Lösen der Bremsen".
Teilstrecken-/Gesamtentfernung
Wegstrecke bis zum ersten Ziel eines abfliegenden Luftfahrzeugs; gilt als Kennziffer für die Luftfahrzeugmasse.
Triebwerksleistungseinstellung
Wert deslärmbezogenen Leistungsparameters, der zur Ermittlung der Schallemission aus den NPD-Daten verwendet wird.
Verfahrensschritte
Vorgabe für das Fliegen eines Profils - die Schritte umfassen auch Änderungen der Geschwindigkeit und/oder der Höhe z.
Wahre Fluggeschwindigkeit (True Airspeed (TAS))
Tatsächliche Geschwindigkeit eines Luftfahrzeugs bezogen auf die umgebende Luft (= Geschwindigkeit über Grund bei Windstille).
Weicher Grund
Eine akustisch "weiche" und in der Regel grasbedeckte Bodenoberfläche, die die meisten Flugplätze umgibt. Akustisch harte, d. h. stark reflektierende Bodenoberflächen sind etwa Beton und Wasser. Die hier beschriebene Methodik für Lärmkonturen gilt für weiche Bodenverhältnisse.
1.2 Symbole
Tabelle 1: Formelzeichen, Einheiten und Bedeutung
| Formelzeichen | Einheit | Bedeutung |
| d | m | Kürzester Abstand vom Immissionsort zu einem Flugbahnsegment |
| dp | m | Schrägabstand vom Immissionsort zu einer Flugbahn |
| dλ | m | Skalierter Abstand |
| Fn | lbf, N, % | Tatsächlicher Nettoschub pro Triebwerk |
| Fn/ δ | lbf, N, % | Korrigierter Nettoschub je Trieb werk |
| H | ft bzw. m | Flughöhe über NN |
| Lp (t) | dB | Schalldruckpegel zum Zeitpunkt t |
| Lpa(t) | dB (A) | A-bewerteter Schalldruckpegel zum Zeitpunkt t |
| LpAE | dB(A) | Schallexpositionspegel, A-bewertet (SEL) |
| LpE | dB | unbewerteter Schallexpositionspegel |
| LpAE∞ | dB(A) | Aus den NPD-Daten ermittelter Schallexpositionspegel (Basispegel) |
| Lpeq | dB | Äquivalenter Dauerschallpegel |
| LpAmax | dB(A) | größter aller LpAmax,seg-Werte während eines Ereignisses |
| LpAmax,seg | dB (A) | Korrigierter NPD-Wert des von einem Segment erzeugten Maximalpegel |
| LpAmax(P, d) | dB (A) | Unkorrigierter NPD-Wert des von einem Segment erzeugten Maximalpegels (Basispegel) |
 |
m | Seitlicher Versatz |
| lg | - | Logarithmus zur Basis 10 |
| N | - | Anzahl der Segmente oder Teilsegmente |
| pA (t) | Pa | A-bewerteter, momentaner Schalldruck |
| po | Pa | Bezugsschalldruck |
| P | lbf, %, sonstige | Leistungsparameter in NPD-Variablen L (P , d) |
| Pseg | lbf, %, sonstige | Für ein bestimmtes Segment maßgebender Leistungsparameter |
| q | m | Abstand vom Beginn eines Segments zum Punkt des kleinsten Vorbeiflugabstands |
| R | m | Kurvenradius |
| S | - | Standardabweichung |
| s | m | Streckenkoordinate (Entfernung zum Bahnbezugspunkt entlang des Kurses über Grund), positiv orientiert in die vom Flugplatz wegführende Richtung |
| s" | m | Streckenkoordinate (Entfernung zum Luftfahrzeugbezugspunkt entlang des Kurses über Grund), positiv orientiert in die vom Flugplatz wegführende Richtung |
| SRWY | m | Länge der Start- und Landebahn |
| t | s | Zeit |
| te | s | Effektive Dauer eines Einzelschallereignisses |
| to | s | Referenzzeit für integrierten Schallpegel |
| τ | S | Zeitkonstante,τ = 1S |
| v(η) | - | Verteilungsfunktion |
| V | kn bzw. m/s | Geschwindigkeit über Grund |
| Vseg | kn bzw. m/s | Äquivalente Geschwindigkeit über Grund für ein bestimmtes Segment |
| Vref | kn bzw. m/s | Referenzgeschwindigkeit über Grund, für die NPD-Daten definiert sind |
| x, y, z | ft bzw. m | Lokale Koordinaten |
| XARP, YARP, ZARP | m | Position des Flugplatzbezugspunkts in geografischen Koordinaten |
| z | ft bzw. m | Höhe des Luftfahrzeugs über Grundebene/Flugplatzbezugspunkt |
| h | ft bzw. m | Höhe der äquivalenten, horizontalen Flugbahn des Luftfahrzeugs über Grundebene/Flugplatzbezugspunkt |
| α | - | Parameter für die Berechnung Segmentkorrektur ΔF |
| β | ° | Höhenwinkel des Luftfahrzeugs zur Grundebene |
| ε | ° | Luftfahrzeug-Querneigungswinkel |
| γ | ° | Steig-/Sinkflugwinkel |
| Φ | ° | Depressionswinkel (Parameter der seitlichen Richtwirkung) |
| λ | m | Gesamtlänge eines Segments |
| ψ | ° | Winkel zwischen der Richtung der Flugbewegung und der Richtung zum Immissionsort |
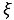 |
° | Steuerkurs des Luftfahrzeugs, gemessen im Uhrzeigersinn ausgehend von Magnetisch-Nord |
| η | - | Normierte Längenkoordinate |
| δ | - | δ = p/po, Verhältnis des Umgebungsluftdrucks auf Immissionsorthöhe zum Standardluftdruck auf Meereshöhe:po = 1.013,25 hPa (oder 1.013,25 mb) |
| θ | - | das Verhältnis der Jahresdurchschnittslufttemperatur auf Immissionsorthöhe zur Standardlufttemperatur auf Meereshöhe:To = 15,0 °C |
Λ(β, ) ) |
dB | Luft-Boden-Dämpfung zur Seite |
| Λ(β) | dB | Luft-Boden-Dämpfung zur Seite bei großer Reichweite |
Γ( ) ) |
- | Abstandsfaktor bei der Dämpfung zur Seite |
| Δ | - | Änderung des Wertes einer Größe oder Korrektur (je nach Angabe im Text) |
| ΔF | dB | Segmentkorrektur ΔF |
| ΔΙ | dB | Korrektur aufgrund der Triebwerksanbringung |
| Δi | - | Bewertung für i-te Tageszeit |
| ASOR | dB | Korrektur am Start-of-Roll-Punkt |
| AV | dB | Dauerkorrektur (Geschwindigkeit) |
Tabelle 2: Indizes und Bedeutung
| Index | Bedeutung |
| 1, 2 | Tiefgestellte Indizes zur Kennzeichnung der Anfangs- und Endwerte eines Intervalls oder Segments |
| E | Exposition |
| i | Summationsindex für Luftfahrzeugmuster/-kategorie |
| j | Summationsindex für Kurs/Teilkurs über Grund |
| k | Summationsindex für Segment |
| max | Höchstwert |
| ref | Bezugswert |
| seg | Spezifischer Wert für ein Segment |
| SOR | Bezogen auf Start-of-Roll-Punkt |
| TO | Start (Take-Off) |
2 Qualitätsrahmen
2.1 Genauigkeit der Eingangswerte
Alle Eingangswerte, die den Emissionspegel einer Quelle beeinflussen, sind mit mindestens der Genauigkeit zu bestimmen, die einer Unsicherheit von ±2 dB (A) im Emissionspegel der Quelle entspricht (wobei alle anderen Parameter unverändert bleiben).
2.2 Verwendung von Standardwerten
Die Eingangsdaten für die Berechnung entsprechen der tatsächlichen Nutzung. Der Kurs über Grund wird grundsätzlich aus Radardaten abgeleitet.
2.3 Qualität der für die Berechnungen verwendeten Software
Die für die Berechnung verwendeten Softwareprodukte müssen die normgerechte Abbildung dieser Vorschrift sicherstellen; dies kann erfolgen in Anlehnung an die DIN 45687:2006-05, Akustik - Software-Erzeugnisse zur Berechnung der Schallimmissionen im Freien - Qualitätsanforderungen und Prüfbestimmungen.
Die Qualitätssicherung gilt ausschließlich für die Verwendung von Fixpunktprofilen. Werden Flugprofile durch Synthese (prozedurale Profile) erstellt, müssen bei der Berechnung Annahmen getroffen werden, die durch eine Qualitätssicherung bisher nicht abgedeckt sind.
3 Ziel und Anwendungsbereich
Mit der "Berechnungsmethode für den Umgebungslärm von Flugplätzen (BUF)" können die LärmindizesLDEN (Tag-Abend-Nacht-Lärmindex) undLNight (Nacht-Lärmindex) der Verordnung über die Lärmkartierung ( 34. BImSchV) für den Flugverkehr berechnet werden, die für die Kartierung von Umgebungslärm nach § 47c des Bundes-Immissionsschutzgesetzes benötigt werden. Die Datengrundlage, die eine Vielzahl von Flugzeugen umfasst, ist in der "Datenbank für die Berechnungsmethode für den Umgebungslärm von Flugplätzen ( BUF-D)" dargestellt.
Die BUF gilt nicht für Schallberechnungen nach dem Gesetz zum Schutz gegen Fluglärm ( Fluglärmgesetz).
Fluglärmkonturen zeigen die Ausdehnung und den Umfang der Fluglärmauswirkungen in der Umgebung von Flugplätzen, wobei die Auswirkungen durch die Werte bestimmter Pegelgrößen ausgewiesen werden. Eine Kontur ist eine Linie, entlang der der Pegelwert konstant ist. Die IndexwerteLDEN, LDay,LEvening undLNight aggregieren sämtliche Fluglärmereignisse, die in der Erhebungszeit von einem Jahr auftreten.
Der Lärm an bodennahen Punkten aufgrund an- und abfliegender Luftfahrzeuge eines nahe gelegenen Flugplatzes hängt von vielen Faktoren ab. Die wichtigsten davon sind Luftfahrzeug- und Triebwerksmuster, die Verfahren für Schub-, Landeklappen- und Geschwindigkeitssteuerung an Bord der jeweiligen Luftfahrzeuge, die Abstände zwischen den Immissionsorten und den verschiedenen Flugbahnen sowie topografie und Wetter vor Ort. Im Flugplatzbetrieb sind im Allgemeinen verschiedene Luftfahrzeugmuster, verschiedene Flugverfahren sowie die verschiedensten Betriebsmassen vertreten.
Es wird ausführlich erläutert, wie Maximal- und Schallexpositionspegel einzelner Luftfahrzeuge an einem Immissionsort jeweils für einen bestimmten Flug zu berechnen sind. Für die Ermittlung der oben erwähnten Lärmindizes (LDEN,LDay,LEvening undLNight) werden die Schallexpositionspegel sämtlicher Fluglärmereignisse an einem Immissionsort energetisch addiert. Wird der Lärmindex für alle Immissionsorte eines Rasters innerhalb des betreffenden Gebietes bestimmt, ergeben sich daraus die Fluglärmkonturen. Nicht lärmerhebliche Ereignisse (d. h. Ereignisse, die nicht wesentlich zum Gesamtwert beitragen) können ausgeschlossen werden, um größtmögliche Effizienz zu sichern.
Wenn lärmerzeugende Tätigkeiten im Zusammenhang mit dem Flugplatzbetrieb nicht wesentlich zur Gesamtexposition der Bevölkerung gegenüber Fluglärm und entsprechenden Fluglärmkonturen beitragen, können sie ausgenommen werden. Zu diesen Tätigkeiten gehören: Rollverkehr, Triebwerksprobeläufe sowie der Einsatz von Hilfstriebwerken (Auxiliary Power Units, APUs). Wenn die Auswirkungen nicht unerheblich sind, kann eine Bewertung der Quellen gemäß Abschnitt 24 durchgeführt werden.
4 Überblick über das Berechnungsverfahren
Der Prozess der Lärmkonturengenerierung ist in Abbildung 1 dargestellt. Fluglärmkonturen bei der Lärmkartierung dienen dem Zweck, die in der Beurteilungszeit aufgetretenen Fluglärmimmissionen ortsaufgelöst darzustellen. Die Fluglärmkonturen werden aus Flugbetriebsaufzeichnungen generiert. Fluglärmkonturen für künftige Planungen beruhen notwendigerweise auf Prognosen des Verkehrs und der Flugwege sowie der Leistungs- und Lärmwerte künftiger Luftfahrzeuge.
Abbildung 1: Der Prozess der Lärmkonturengenerierung

Jeder Anflug und jeder Abflug wird durch eine bestimmte Flugbahngeometrie und die Lärmemission des Luftfahrzeugs entlang dieser Bahn charakterisiert. Die Lärmemission hängt von den Eigenschaften des Luftfahrzeugs ab - hauptsächlich von der Triebwerksleistung. Für die Berechnung des Schallexpositionspegels wird die Flugbahn in Segmente unterteilt. In den Abschnitten 5 bis 8 werden die Elemente der Methodik vorgestellt, und es wird der Grundsatz der Segmentierung erläutert, auf dem sie beruht: Der Schallexpositionspegel ist eine Aggregation aller "lärmerheblichen" Segmente der Flugbahn, die sich jeweils unabhängig voneinander berechnen lassen. Die Abschnitte 5 bis 8 umreißen zudem die Anforderungen an die Eingabedaten für die Erstellung von Fluglärmkonturen. Detaillierte Spezifikationen für die benötigten Betriebsdaten sind in Anhang a aufgeführt.
Wie die Flugbahnsegmente aus vorbehandelten Eingabedaten berechnet werden, wird in den Abschnitten 9 bis 15 dargelegt. Dazu gehören Anwendungen der Flugleistungsanalyse, für die entsprechende Gleichungen in Anhang B aufgeführt sind. Die Flugbahnen weichen deutlich voneinander ab, d. h. Luftfahrzeuge auf einer Flugroute bewegen sich aufgrund der Wirkungen unterschiedlicher atmosphärischer Bedingungen, Luftfahrzeugmassen und Betriebsverfahren, Fluglotsenanweisungen usw. in einem breiteren Korridor. Dem wird Rechnung getragen, indem die einzelnen Flugbahnen statistisch beschrieben werden, und zwar als "Kernbahn", die sich in Begleitung mehrerer Streubahnen befindet. Auch dies wird in den Abschnitten 9 bis 15 unter Bezugnahme auf zusätzliche Informationen in Anhang C erläutert.
In den Abschnitten 16 bis 21 werden die Schritte aufgeführt, die bei der Berechnung des Maximal- und Schallexpositionspegels eines Einzelereignisses zu befolgen sind. Anhang D hat die Neuberechnung von NPD-Daten für Nicht-Referenz-Bedingungen zum Gegenstand. Anhang E erläutert die akustische Dipolquelle, die im Modell zur Bestimmung der Schallabstrahlung von Flugbahnsegmenten finiter Länge verwendet wird.
Die Anwendung der in den Abschnitten 9 bis 21 beschriebenen Algorithmen erfordert neben den entsprechenden Flugbahnen geeignete Lärm- und Leistungsangaben für die betreffenden Luftfahrzeuge.
Den Kern der Berechnung bildet die Bestimmung des Schallexpositionspegels einer einzelnen Flugbewegung an einem Immissionsort Sie ist für alle Flugbewegungen an jedem Punkt eines vorgeschriebenen Bereichs zu wiederholen, der sich über die erwartete Ausdehnung der Fluglärmkonturen erstreckt. An jedem Punkt werden die Schallexpositionspegel so aggregiert oder gemittelt, dass sich ein "kumulativer Pegel" oder ein Lärmindexwert ergibt. Dieser Teil des Prozesses wird in den Abschnitten 25 bis 27 beschrieben.
In Abschnitt 28 werden die Optionen und Anforderungen für die Anpassung von Lärmkonturen an Felder von Lärmindexwerten zusammengefasst.
5 Das Konzept der Segmentierung
Die BUF-D enthält für viele Luftfahrzeuge NPD-Basisbeziehungen (Noise-Power-Distance). Darin werden für einen stationären Geradeausflug bei einerBezugsgeschwindigkeit unter ausgewiesenenatmosphärischen Bezugsbedingungen sowie in einer bestimmten Luftfahrzeugkonfiguration Maximalpegel als auch Schallexpositionspegel direkt unterhalb des Luftfahrzeugs 1 als Funktion des Abstands aufgeführt. Zu Lärmberechnungszwecken wird die Antriebsleistung durch einenlärmbezogenen Leistungsparameter dargestellt; im Allgemeinen wird hierfür derkorrigierte Nettoschub verwendet. Die der Datenbank entnommenen Basispegel werden korrigiert, um erstens Unterschiede zwischen Real- und Referenzbedingungen der Atmosphäre und der Luftfahrzeuggeschwindigkeit (bei Schallexpositionspegeln) und zweitens Unterschiede zwischen nach unten und seitwärts abgestrahltem Lärm zu berücksichtigen. Der letztgenannte Unterschied geht auf dielaterale Richtcharakteristik (Triebwerksanbringungseffekte) und dieseitliche Dämpfung zurück. Die auf diese Weise korrigierten Pegel gelten jedoch weiterhin nur für den Gesamtschallpegel des Luftfahrzeugs im stationären Horizontalflug.
Um den Lärm zu berechnen, der auf einen Immissionsort von einer nicht gleichförmigen Flugbahn einwirkt, wird die Flugbahn durch eine Reihe zusammenhängender geradliniger Segmente dargestellt, die sich jeweils als endlicher Teil einer unendlichen Bahn betrachten lassen und für die NPD-Daten sowie die lateralen Korrekturen bekannt sind. Der Maximalpegel des Ereignisses LpAmax entspricht dem größten Wert der MaximalsegmentpegelLpAmax,seg. Die Berechnung des zeitintegrierten Pegels des gesamten Schallereignisses erfolgt durch logarithmische Addition der SchallexpositionssegmentpegelLpAE,seg der Segmente, die einen wesentlichen Beitrag zum Gesamtschallereignis leisten.
Der Anteil, den ein endliches Segment zum Schallexpositionspegel beiträgt, wird empirisch abgeschätzt. DerEnergieanteil F - der als Anteil am gesamten unendlichen Flugbahnschall ausgedrückte Segmentschall - berücksichtigt die longitudinale Richtcharakteristik vom Fluglärm und die "Sicht" vom Immissionsort auf das Segment.
6 Flugbahnen: Strecken und Profile
Im Modellierungskontext ist eineFlugbahn (Trajektorie) die vollständige Beschreibung der Bewegung des Luftfahrzeugs in Raum und Zeit 2. Zur Berechnung des erzeugten Lärms ist die Kenntnis der Flugbahn sowie des Triebwerksschubs oder einem anderen lärmbezogenen Leistungsparameter erforderlich. DerKurs über Grund ist die vertikale Projektion der Flugbahn auf eine ebene Bodenfläche. In Kombination mit dem vertikalenFlugprofil ergibt sich daraus die dreidimensionale Flugbahn. Für die Berechnung der Schallexpositionspegel wird die Flugbahn jeder Flugbewegung durch eine Reihe von zusammenhängenden geraden Segmenten beschrieben. Jedes Segment muss durch die geometrischen Koordinaten seiner Endpunkte sowie die entsprechenden Geschwindigkeits- und Triebwerksleistungsparameter des Luftfahrzeugs definiert werden. Flugbahnen und Triebwerksleistung lassen sich auf verschiedene Weise bestimmen, vor allem mit
Für dieSynthese der Flugbahn (a) bedarf es der Kenntnis des Kurses über Grund und seiner lateralen Streuung, der Luftfahrzeugmasse, der Geschwindigkeits-, Landeklappen- und Schubsteuerungsverfahren, der Flugplatzhöhe, des Windes und der Lufttemperatur. Gleichungen zur Berechnung des Flugprofils anhand der erforderlichen Antriebs- und aerodynamischen Parameter sind in Anhang B aufgeführt. Jede Gleichung enthält Koeffizienten und/oder Konstanten, die auf empirischen Daten für jedes spezifische Luftfahrzeugmuster basieren. Die Gleichungen der aerodynamischen Leistung in Anhang B erlauben die Prüfung einer sinnvollen Kombination von Luftfahrzeugbetriebsmasse und Flugverfahren, einschließlich Betrieb mit verschiedenen Bruttostartmassen.
DieAnalyse der gemessenen Daten (b), z.B. von Flugdatenschreibern, Radar- oder sonstigen Flugverfolgungssystemen beinhaltet ein "Reverse Engineering", d. h. eine Umkehr des Syntheseprozesses (a). Statt einer Schätzung des Luftfahrzeug- und Triebwerkszustands an den Enden der Flugsegmente durch Integration der Effekte der auf die Luftfahrzeugzelle wirkenden aerodynamischen und Schubkräfte, werden die Kräfte durch eine Ableitung der Änderungen von Höhe und Geschwindigkeit der Zelle geschätzt. Verfahren für die Verarbeitung der Flugbahninformationen werden in Abschnitt 14 beschrieben.
Bei einer Lärmmodellierungsanwendung könnte jeder Einzelflug theoretisch eigenständig dargestellt werden; dies würde eine genaue Berücksichtigung der räumlichen Streuung der Flugbahnen gewährleisten. Um jedoch die Datenaufbereitung und die Rechenzeit innerhalb vertretbarer Grenzen zu halten, werden Flugbahnstreubereiche durch eine Gruppe von seitlich versetzten "Unterstrecken" dargestellt, neben der Kernstrecke sind vierzehn Unterstrecken zu definieren. Die vertikale Streuung wird bereits implizit durch die Auswirkungen unterschiedlicher Luftfahrzeugmassen auf die Höhenprofile berücksichtigt.
7 Lärm- und Leistungsangaben
Die BUF-D enthält Lärm- und Leistungsdaten für die meisten vorhandenen Luftfahrzeugmuster. Muster und Varianten, für die derzeit keine Daten verzeichnet sind, werden durch Luftfahrzeuge, die ähnliche Fluglärmkonturen erzeugen, also lärmäquivalent sind, substituiert.
Die BUF-D enthält zudem vorgegebene "Verfahrensschritte", die den Aufbau von Flugprofilen für mindestens ein übliches lärmminderndes Abflugverfahren ermöglichen. Neuere Datenbankeinträge erfassen zwei unterschiedliche lärmmindernde Abflugverfahren.
8 Flugplatz- und Flugbetrieb
Für die Ermittlung der Fluglärmbelastung in der Umgebung von Flugplätzen sind insbesondere die im Folgenden aufgeführten Eingangsdaten relevant.
1) Allgemeine Flugplatzdaten
2) Start-/Landebahndaten
Für jede Start-/Landebahn:
3) Streckendaten
Projizierte Flugstrecken (Kurs über Grund) werden durch eine Folge von Koordinaten in der Grundebene beschrieben. Durch statistische Analyse der Radardaten wird zur Darstellung der lateralen Streuung eine Kernstrecke (backbone track) mit vierzehn Unterstrecken ermittelt. Sind keine Radardaten verfügbar, werden die Kernstrecken in der Regel aus geeigneten Verfahrensinformationen aufgebaut, z.B. unter Verwendung von Standard-Instrumentenabflugverfahren aus Luftfahrthandbüchern ermittelt. Diese konventionelle Beschreibung enthält die folgenden Informationen:
Diese Informationen sind das notwendige Minimum zur Bestimmung der Kernstrecke. Zusätzlich ist die laterale Streuung darzustellen, wobei die folgenden Informationen benötigt werden:
4) Luftverkehrsdaten
Luftverkehrsdaten sind
Lärmindizes, die sich auf einen bestimmten Tageszeitabschnitt beziehen, spiegeln Lärmereignisse als mittlere tägliche Werte zu bestimmten Tageszeiten (z.B. Tag, Abend und Nacht) wider (siehe Abschnitte 25 bis 27).
5) topografische Daten
Die Änderungen der Geländehöhe werden durch die Verwendung eines digitalen Geländemodells berücksichtigt.
ANMERKUNG: Die Angaben für die Geländehöhen werden in der Regel als Satz vonx-, y-, z-Koordinaten für ein rechteckiges Gitter mit bestimmter Maschenweite bereitgestellt. Dabei werden sich die Parameter des Höhengitters wahrscheinlich von den Parametern des für die Lärmberechnung genutzten Gitters unterscheiden. In diesem Fall können die geeigneten z-Koordinaten im letztgenannten Gitter mittels linearer Interpolation geschätzt werden.
6) Bezugsbedingungen
Die internationalen Lärm- und Leistungsangaben für Luftfahrzeuge werden auf Standardbezugsbedingungen normalisiert, die für Flugplatzlärmstudien vielfach verwendet werden (siehe Anhang D).
ANMERKUNG: Standardisierte Luftfahrzeugschallmessungen erfolgen 1,2 m über der Erdoberfläche. Dies braucht jedoch nicht besonders berücksichtigt werden, da für Modellierungszwecke angenommen werden kann, dass Maximal- und Schallexpositionspegel gegenüber der Immissionsorthöhe relativ unempfindlich sind 4.
NPD-Daten können auch bei abweichenden Bedingungen angewendet werden, wenn die mittleren bodennahen Bedingungen innerhalb des folgenden Rahmens liegen:
Obgleich die Aerodynamik- und Triebwerksdaten in den Tabellen 7 bis 9 der BUF-D auf diesen Bedingungen basieren, können sie für andere Flugplatzbezugshöhen und andere mittlere Lufttemperaturen in EU-Staaten verwendet werden, ohne die Genauigkeit der berechneten Konturen des kumulativen mittleren Schallpegels wesentlich zu beeinträchtigen (siehe Anhang B).
Die Berechnung der Start- und Steigflugprofile unter Verwendung der in Anhang B beschriebenen Verfahren muss auf der Bruttostartmasse basieren.
9 Beschreibung der Flugbahn
Bei diesem Fluglärmberechnungsverfahren wird jede Flugbewegung durch ihre dreidimensionale Flugbahn und die dabei eingesetzte Triebwerksleistung und Geschwindigkeit beschrieben. Diese kann selbst Teil der Streuung einer Flugroute sein, die zur Modellierung des Korridors verwendet werden. Der Korridor, die Vertikalprofile und die Luftfahrzeugbetriebsparameter werden aus den eingegebenen Szenariodaten zusammen mit den Luftfahrzeugdaten aus der BUF-D ermittelt. Die NPD-Daten in der BUF-D definieren Lärm von Luftfahrzeugen, die sich auf idealisierten horizontalen Flugbahnen unendlicher Länge bei konstanter Geschwindigkeit und Triebwerksleistung bewegen. Zur Anpassung dieser Daten an auf Flugplätzen übliche Flugbahnen, die durch häufige Änderungen der Antriebsleistung und der Geschwindigkeit gekennzeichnet sind, wird jede Flugbahn in endliche geradlinige Segmente unterteilt, deren Beiträge zum auftretenden Lärm anschließend am Immissionsort addiert werden.
10 Verhältnis zwischen Flugbahn und Luftfahrzeugkonfiguration
Die dreidimensionale Flugbahn einer Flugbewegung bestimmt die geometrischen Aspekte der Schallabstrahlung und -ausbreitung zwischen Luftfahrzeug und Immissionsort. Die Flugbahn wird beeinflusst von pilotenseitig ausgelösten Schub-, Klappen- und Höhenänderungen zur Einhaltung von Flugrouten sowie von der Flugverkehrskontrolle vorgegebenen Höhen und Geschwindigkeiten entsprechend den Standardbetriebsverfahren des Luftfahrzeugbetreibers. Auch die Luftfahrzeugmasse und atmosphärische Bedingungen beeinflussen die Flugbahn. Die Anweisungen und Handlungen unterteilen die Flugbahn in Streckenabschnitte, die Segmente bilden. In der horizontalen Ebene umfassen sie Geradeausflugabschnitte, angegeben als Distanz bis zum Beginn der nächsten Kurve, sowie Kurvenflüge, definiert durch Kurvenradius und Kursänderung. In der vertikalen Ebene werden die Segmente durch die vergangene Zeit und/oder die zurückgelegte Entfernung zur Erreichung erforderlicher Änderungen der Vortriebsgeschwindigkeit und/oder Höhe bei vorgegebenen Schubeinstellungen und Klappenstellungen bestimmt. Die entsprechenden vertikalen Koordinaten werden alsProfilpunkte bezeichnet.
Sowohl der horizontale als auch der vertikale Verlauf der Flugbahn wird segmentiert. Der horizontale Verlauf der Flugbahn (d. h. ihre zweidimensionale Projektion auf die Erdoberfläche) ist derKurs über Grund, definiert durch die Anflug- oder Abflugstreckenführung. Der durch die Profilpunkte gegebene vertikale Verlauf und die dazugehörigen Flugparameter Geschwindigkeit, Querneigungswinkel und Schubeinstellung definieren insgesamt dasFlugprofil, das vomFlugverfahren abhängt. Die Flugbahn wird durch Zusammenführen des 2-D-Flugprofils mit dem 2-D-Kurs über Grund konstruiert, so dass sich eine Folge von 3-D-Flugbahnsegmenten ergibt.
Es sei daran erinnert, dass das Profil für eine bestimmte Reihe von Verfahrensschritten vom Kurs über Grund abhängt. So ist z.B. die Steigrate bei gleichem Schub und gleicher Geschwindigkeit im Kurvenflug geringer als im Geradeausflug. Es ist wichtig, die für Kurvenflüge notwendigen Änderungen des Querneigungswinkels zu bestimmen, da sich dies in bedeutendem Maße auf die Richtwirkung der Schallemission auswirkt.
Der von einem Flugbahnsegment an einem Immissionsort ankommende Schall hängt von der Geometrie des Segments bezogen auf den Immissionsort und von der Luftfahrzeugkonfiguration ab. Diese stehen jedoch in Wechselwirkung - eine Änderung des einen Faktors bewirkt eine Änderung des anderen, und so muss sichergestellt werden, dass die Konfiguration des Luftfahrzeugs an allen Punkten der Flugbahn mit seiner Bewegung entlang der Bahn im Einklang steht.
In Anhang B finden sich die Gleichungen, mit denen die auf ein Luftfahrzeug wirkenden Kräfte und seine Bewegung in Beziehung gesetzt werden; außerdem wird darin erläutert, wie sie gelöst werden, um die Eigenschaften der Segmente, aus denen sich Flugbahnen zusammensetzen, zu bestimmen. Die verschiedenen Arten von Segmenten und die entsprechenden Abschnitte von Anhang B lauten:
Bei der Berücksichtigung der Flugstreckenstreuung haben Unterstrecken und Kernstrecke das gleiche Flugprofil und die gleichen Luftfahrzeugkonfigurationen.
11 Quelle der Flugbahndaten
Zwar können Flugdatenschreiber qualitativ hochwertige Daten liefern, doch sind diese für Lärmmodellierungszwecke schwer zu beschaffen.Radardaten sind daher die wichtigste Informationsquelle für die Modellierung der Streuung tatsächlich geflogener Flugbahnen. 5 Nähere Einzelheiten sind in Anhang A dargestellt.
12 Koordinatensysteme
12.1 Lokales Koordinatensystem
Das lokale Koordinatensystem (x, y, z) ist kartesisch und hat seinen Ursprung (0,0,0) am Flugplatzbezugspunkt (XARP,YARP, ZARP), wobeiZARP die Flugplatzbezugshöhe ist undz = 0 die Grundebene (Horizontalebene) bezeichnet, auf der in der Regel Fluglärmkonturen berechnet werden. Alle Immissionsorte, das Berechnungsgitter und die Lärmkontur punkte werden in lokalen Koordinaten ausgedrückt 6.
12.2 Streckenkoordinatensystemes unds"
Längen auf den Flugstrecken werden durch die Streckenkoordinatens unds" ausgedrückt. Die Koordinate s ist für jeden Kurs über Grund (projizierte Flugstrecke) spezifisch und stellt die entlang der Strecke in die vom Flugplatz wegführende Richtung gemessene Entfernung zum Bahnbezugspunkt PB dar. Die Streckenkoordinates" wird vom Luftfahrzeugbezugspunkt PF aus (bei Abflugstrecken ab Start-of-Roll-Punkt, bei Anflugstrecken ab Landeschwelle) unabhängig von der Flugrichtung in der vom Flugplatz wegführenden Richtung positiv gezählt. Somit wirds" negativ in Bereichen hinter dem Start-of-Roll-Punkt beim Abflug und nach Überquerung der Landeschwelle beim Anflug. Flugbetriebsparameter wie Höhe z, Geschwindigkeit und Schubeinstellung werden als Funktionen vons" ausgedrückt.
Abbildung 2: Streckenkoordinatensystemes unds"

12.3 Berücksichtigung der topografie
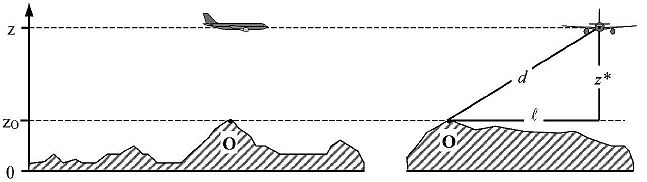
Um die topografie zu berücksichtigen, muss bei der Abschätzung der Ausbreitungsentfernung d die Flughöhenkoordinatez durchz* =z - zo ersetzt werden. Dabei istzo diez-Koordinate des Immissionsortes O. Hierzu wird ein Digitales Geländemodell (DGM) verwendet, wobei zumindest das Digitale Geländemodell für Deutschland (DGM-D) mit einer Gitterweite von 50 m benutzt werden sollte. Sofern detaillierte geographische Daten vorliegen, können diese ergänzend zum DGM-D verwendet werden. Die Geometrie zwischen Luftfahrzeug und Immissionsort ist in Abbildung 3 dargestellt. Zur Definition vond undl siehe Abschnitte 16 bis 21. 7
Abbildung 3: Bodenerhöhung längs (links) und seitlich (rechts) des Kurses über Grund. (Die Grundebenez = 0 verläuft durch den Flugplatzbezugs punkt. 0 ist der Immissionsort).
13 Projizierte Flugstrecken (Kurs über Grund)
13.1 Kernstrecken (backbone track)
Die Kernstrecke (backbone track) definiert das Zentrum des Korridors entlang derer sich ein Luftfahrzeug auf einer bestimmten Streckenführung bewegt. Für die Zwecke der Fluglärmmodellierung wird der Korridor durch die statistische Analyse von Radardaten festgelegt. Sind keine Radardaten verfügbar werden reglementierende Betriebsdaten herangezogen. Abbildung 4 veranschaulicht die Geometrie einer Flugstrecke mit Kurven und geraden Segmenten.
Abbildung 4: Geometrie der Flugstrecke mit Kurven und geraden Segmenten

13.2 Flugbahnstreuung
Die Flugstrecken werden im Datenerfassungssystem mit Korridorbreiten beschrieben, die die Abweichung der Luftfahrzeuge von der Flugstrecke angeben. Die Korridorbreiten sollten unter Verwendung eines Flugwegaufzeichnungssystems, z.B. FANOMOS (Flight Track and Noise Monitoring System), für die einzelnen Flugstrecken festgelegt werden, sofern dieses System am jeweiligen Flugplatz zur Verfügung steht. Andernfalls sind die Korridorbreiten aufgrund der örtlichen flugbetrieblichen Praxis zu schätzen. Sofern eine derartige Schätzung nicht möglich ist, ist eine Korridoraufweitung vom 0,2-fachen der längs der Flugstrecke zurückgelegten Bogenlänge bis auf einen Wert von 3.000 m anzusetzen.
Zur Berücksichtigung der seitlichen Abweichung der Flüge von der festgesetzten Flugstrecke wird jeder Flugstrecke ein Flugkorridor mit einer Korridorbreiteb(s) zugeordnet. Die Korridorbreiteb(s) wird als stückweise lineare Funktion von s festgesetzt und ist im Datenerfassungssystem angegeben. Die im Datenerfassungssystem durch eine Folge von Geraden und Kreisbögen beschriebene "Soll-Flugstrecke" stellt die Mittellinie des Flugkorridors dar.
Die Verteilung der Flugbahnen im Flugkorridor der Flugstrecke wird durch die Verteilungsfunktion
| v(η) = 30 · ((1/4) -η2)2 | ( 1) |
| mit: | |
| η =(ρ / b(s)) | ( 2) |
beschrieben. Dabei istρ die Längenkoordinate auf der Normalen zur Flugstrecke. Die normierte Längenkoordinateη nimmt innerhalb des Korridors Werte zwischen -1/2 und +1/2 an. Die Verteilung der Flugbewegungen über den Flugkorridor wird durch eine Aufteilung des Korridors in eine ungerade Anzahl von gleich breiten Teilkorridoren realisiert. Abbildung 5 zeigt dies am Beispiel einer Zerlegung in drei Teilkorridore.
Die Mittellinie eines Teilkorridors wird als Flugweg oder Unterstrecke bezeichnet. Die Flugwege und die zugehörigen Teilkorridore werden ausgehend von der Flugstrecke nach außen fortlaufend nummeriert: Die Flugstrecke als Korridormittellinie bekommt die laufende Nummer 1, die links zur Richtung der Flugstrecke liegenden Flugwege erhalten geradzahlige, die rechts davon liegenden Flugwege ungeradzahlige Nummern. Für die Fluglärmberechnungen sind 15 Teilkorridore zu Grunde zu legen.
Abbildung 5: Beschreibung eines Flugkorridors durch Teilkorridore und Flugwege
(beispielhaft für eine Zerlegung in drei Teilkorridore)
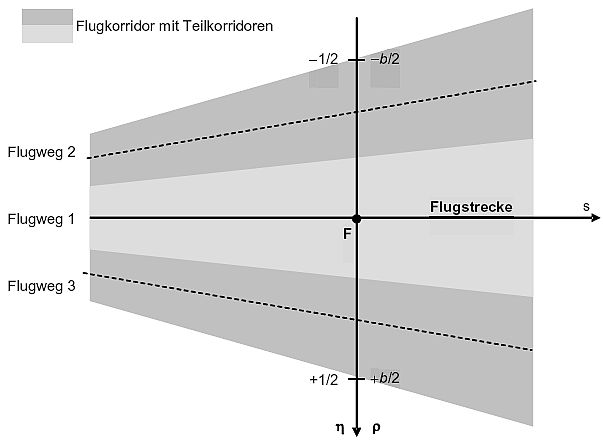
Der Anteil der Vorbeiflüge von Luftfahrzeugen auf einem Flugweg (also innerhalb eines Teilkorridors) an der Anzahl der auf der Flugstrecke verkehrenden Luftfahrzeuge ergibt sich durch Integration der Verteilungsfunktionv(η) über den Teilkorridor (sog. Unterstrecke). Tabelle 3 zeigt diese Anteile für die Zerlegung in 15 Unterstrecken.
Tabelle 3: Parameter für die Zerlegung eines Korridors in 15 Unterstrecken; Kernstrecke = Unterstrecke 1
| Flugweg Nr. | η-Koordinate des Flugwegs | Anteil an Flugbewegungen [%] |
| 1 | 0,000 | 12,48 |
| 2 / 3 | -/+ 0,067 | 12,02 |
| 4 / 5 | -/+ 0,133 | 10,76 |
| 6 / 7 | -/+ 0,200 | 8,80 |
| 8 / 9 | -/+ 0,267 | 6,39 |
| 10 / 11 | -/+ 0,333 | 3,87 |
| 12 / 13 | -/+ 0,400 | 1,65 |
| 14 / 15 | -/+ 0,467 | 0,27 |
Die vertikale Streuung wird nicht als eigenständige Variable modelliert.
14 Flugprofile
Das Flugprofil ist eine Beschreibung der Bewegung des Luftfahrzeugs in der vertikalen Ebene über dem Kurs über Grund in Bezug auf Position, Geschwindigkeit, Querneigungswinkel und Triebwerksleistungseinstellung.
Grundsätzlich sind die in der BUF-D aufgeführten Fixpunktprofile zu verwenden. Weichen lokale Bedingungen von den in der BUF-D angegeben Standardbedingungen ab, sind auf die Situation angepasste Fixpunktprofile zu berechnen, wie im Folgenden erläutert wird.
Um einen hohen Genauigkeitsgrad zu erreichen, müssen die Profile den jeweiligen Flugbetriebszustand so exakt wie möglich widerspiegeln. Dazu bedarf es zuverlässiger Angaben über die atmosphärischen Bedingungen, die Luftfahrzeugmuster und -varianten sowie die Betriebsverfahren - die unterschiedlichen Schubeinstellungen und die Klappenstellung sowie den gefundenen Kompromiss zwischen Höhen- und Geschwindigkeitsänderung - alle über die betreffenden Zeitabschnitte entsprechend gemittelt.
Die Synthese von Flugprofilen anhand von "Verfahrensschritten" aus der BUF-D oder von Luftfahrzeugbetreibern wird in Abschnitt 15 und Anhang B beschrieben. Dieser Prozess ergibt sowohl die Flugbahngeometrie, als auch die entsprechenden Geschwindigkeits- und Schubänderungen. Es wird angenommen, dass alle gleichartigen Luftfahrzeuge in einem Korridor unabhängig davon, ob sie der Kernstrecke oder den verstreuten Unterstrecken zugewiesen sind, dem gleichen Kernstreckenprofil folgen.
ANMERKUNGEN: Neben der BUF-D, die Standardinformationen zu den Verfahrensschritten liefert, sind die Luftfahrzeugbetreiber die beste Quelle für zuverlässige Informationen, das heißt zu den von ihnen verwendeten Verfahren und den typischen geflogenen Luftfahrzeugmassen. Die wertvollste Quelle für Einzelflüge stellt der Flugdatenschreiber dar, der sämtliche relevante Informationen liefert. Doch selbst wenn derartige Daten verfügbar sind, ist der Aufwand für ihre Aufbereitung enorm hoch. Im Sinne des notwendigen sparsamen Umgangs mit Ressourcen bei der Modellierung besteht daher die normale praktische Lösung darin, fundierte Annahmen zu mittleren Massen und Betriebsverfahren anzustellen.
Bei einer Übernahme von in der BUF-D angegebenen Standard-Verfahrensschritten ist Vorsicht geboten. Es handelt sich dabei zwar um standardisierte Verfahren, denen vielfach gefolgt wird, die aber vom Betreiber in konkreten Fällen vielleicht nicht angewendet werden. Ein wichtiger Faktor ist die Festlegung des Start- und Steigschubs. Insbesondere ist es üblich, den Schub während des Abflugs (gegenüber Volllast) zurückzunehmen, um die Lebensdauer der Triebwerke zu verlängern. Anhang B vermittelt Hinweise zur Darstellung der typischen Praxis; daraus ergeben sich im Allgemeinen realistischere Konturen als bei Annahme von Vollschub. Ist die Startbahn jedoch kurz und/oder ist die durchschnittliche Lufttemperatur hoch, dürfte es realistischer sein, von Vollschub auszugehen.
Eine höhere Genauigkeit bei der Modellierung tatsächlicher Szenarien lässt sich erreichen, wenn die nominalen Informationen durch die Anwendung von Radardaten ergänzt oder ersetzt werden. Flugprofile lassen sich ähnlich wie die seitlichen Kernstrecken anhand von Radardaten bestimmen - allerdings erst nach einer Aufteilung des Verkehrs nach Luftfahrzeugmuster und -variante und mitunter nach Masse und Teilstreckenlänge (nicht jedoch nach Streuung) - so dass sich für jede Untergruppe ein mittleres Höhen- und Geschwindigkeitsprofil gegenüber der zurückgelegten Strecke über Grund ergibt. Beim anschließenden Zusammenfügen mit den Kursen über Grund wird dieses Einheitsprofil dann in der Regel wieder sowohl der Kernstrecke als auch den Unterstrecken zugewiesen.
Ist die Luftfahrzeugmasse bekannt, kann die Geschwindigkeits- und Schubänderung über eine schrittweise Lösung der Bewegungsgleichungen berechnet werden. Eine vorherige Aufbereitung der Daten ist sinnvoll, um die Effekte von Radarfehlern zu minimieren, aufgrund derer Schätzungen der Beschleunigung unzuverlässig werden können. Der erste Schritt besteht jeweils in einer Neudefinition des Profils durch Einpassung von geradlinigen Segmenten, die die jeweiligen Teilstrecken darstellen. Dabei wird jedes Segment entsprechend klassifiziert, d. h. als Startrollstecke, Steig- oder Sinkflug mit konstanter Geschwindigkeit, Schubrücknahme oder Beschleunigung/Verzögerung mit oder ohne Änderung der Klappenstellung. Zu den notwendigen Eingabedaten gehören zudem die Luftfahrzeugmasse sowie der atmosphärische Zustand.
In Abschnitt 13 wird darauf hingewiesen, dass die seitliche Streuung von Flugstrecken um die nominale bzw. die Kernstrecke herum besonders zu berücksichtigen ist. Die Radarinformationen sind dadurch gekennzeichnet, dass in der vertikalen Ebene ähnliche Streuungen der Flugbahnen auftreten. Es ist allerdings nicht üblich, die vertikale Streuung als eigenständige Variable zu modellieren. Sie entsteht hauptsächlich aufgrund unterschiedlicher Luftfahrzeugmasse und unterschiedlicher Betriebsverfahren, die bei der Aufbereitung der Verkehrseingabedaten berücksichtigt werden.
15 Konstruktion von Flugbahnsegmenten
Jede Flugbahn muss durch eine bestimmte Menge an Segmentkoordinaten (Knotenpunkten) und Flugparametern definiert werden. Die Reihenfolge der Berechnungsschritte ist wie folgt vorgegeben:
In Schritt 3 und 4 erfolgt eine Teilsegmentierung, bei der vorhandene Segmente aus Fixpunktprofil und Kurs über Grund in Teilsegmente zerlegt werden. Um diesen Prozess zu veranschaulichen, wird in Abschnitt 15 von Teilsegmenten gesprochen. Ist die Segmentierung abgeschlossen, wird die Flugbahn zwischen zwei resultierenden Knotenpunkten nur noch mit "Segment" bezeichnet (ab Abschnitt 16).
15.1 Kurs über Grund
Ein Kurs über Grund wird durch eine Reihe von (x, y)-Koordinaten in der Grundebene (z.B. anhand von Radarinformationen) oder durch eine Folge von Flugführungsanweisungen zur Beschreibung gerader Segmente und Kreisbögen (Kurven mit festgelegtem Radiusr und Steuerkursänderung Δ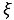 definiert.
definiert.
Für die Segmentierungsmodellierung wird ein Bogen durch eine Folge in Teilbögen eingepasster gerader Segmente dargestellt. In Anhang B.5 wird die Berechnung des Querneigungswinkels während einer stationären Vollkurve erläutert. Näherungsweise wird der Querneigungswinkel unverzögert angelegt, d. h. es gilt Δ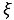 trans = 0 . Der Bogen mit der Steuerkursänderung Δ
trans = 0 . Der Bogen mit der Steuerkursänderung Δ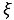 - 2 Δ
- 2 Δ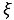 trans wird innsub Teilbögen geteilt, und zwar nach der Gleichung:
trans wird innsub Teilbögen geteilt, und zwar nach der Gleichung:
nsub = int (1 (Δ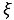 - Δ - Δ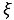 trans) / 10) . trans) / 10) . |
( 3) |
Dabei ist int(x) eine Funktion, die den ganzzahligen Teil vonx ergibt. Die Steuerkursänderung Δ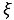 sub jedes Teilbogens errechnet sich dann als
sub jedes Teilbogens errechnet sich dann als
Δ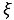 sub = (Δ sub = (Δ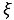 - 2Δ - 2Δ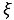 trans) /nsub , trans) /nsub , |
( 4) |
wobeinsub groß genug sein muss, damit Δ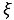 sub ≤ 10° . Die Segmentierung eines Bogens ohne die abschließenden Übergangsteilsegmente wird in Abbildung 6 veranschaulicht 9.
sub ≤ 10° . Die Segmentierung eines Bogens ohne die abschließenden Übergangsteilsegmente wird in Abbildung 6 veranschaulicht 9.
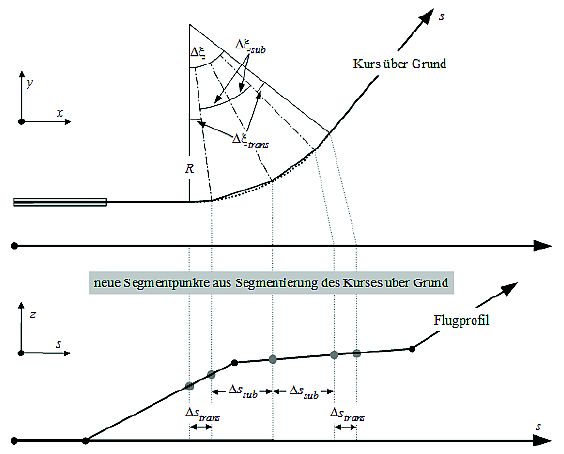
Abbildung 6: Konstruktion von Flugbahnsegmenten zur Teilung der Kurve in Segmente der Länge Δs (obere Ansicht in horizontaler Ebene, untere Ansicht in vertikaler Ebene)
15.2 Flugprofil
Auf die Verwendung des Apostrophs (") zur Kennzeichnung des luftfahrzeugbezogenen Koordinatensystems wird im Folgenden der Einfachheit halber verzichtet. Die Parameter zur Beschreibung jedes Flugprofilsegments am Beginn (Index 1) und am Ende (Index 2) des Segments lauten:
| S1,S2 | Entfernung entlang des Kurses über Grund, |
| Z1,Z2 | Flughöhe über Grund, |
| V1, V2 | Geschwindigkeit über Grund, |
| P1,P2 | lärmbezogener Schubparameter (entspricht dem, für den die NPD-Kurven definiert sind) |
| ε1, ε2 | Querneigungswinkel. |
Die Indizes der Segmente werden wie die Entfernung entlang des Kurses über Grund aus den Fixpunktprofilen unabhängig von der Flugrichtung in der vom Flugplatz wegführenden Richtung gezählt.
ANMERKUNG ZUR VERWENDUNG PROZEDURALER PROFILE:
Zum Aufbau eines Flugprofils aus einer Menge von Verfahrensschritten (Flugbahnsynthese) werden die Segmente aufeinanderfolgend so konstruiert, dass die erforderlichen Bedingungen an den Endpunkten erzielt werden. Dabei werden die Endpunktparameter jedes Segments zu den Anfangspunktparametern des nächsten Segments. Bei jeder Segmentberechnung sind die Parameter am Anfang bekannt; die erforderlichen Bedingungen am Ende werden vom Verfahrensschritt angegeben. Die Schritte selbst sind entweder durch die Standardschritte in der BUF-D oder vom Benutzer festgelegt (z.B. anhand von Luftfahrzeughandbüchern). Bei den Endbedingungen handelt es sich gewöhnlich um Höhe und Geschwindigkeit, und beim Profilaufbau geht es um die Bestimmung der zurückgelegten Strecke unter Erreichung dieser Bedingungen. Die undefinierten Parameter werden über Flugleistungsberechnungen gemäß Anhang B bestimmt.
Verläuft der Kurs über Grund geradeaus, so lassen sich die Profilpunkte und dazugehörigen Flugparameter unabhängig vom Kurs über Grund bestimmen (Querneigungswinkel stets null). Allerdings verläuft der Kurs über Grund selten geradeaus. Meist treten Kurven auf, die zur Erzielung bester Ergebnisse bei der Bestimmung des zweidimensionalen Flugprofils berücksichtigt werden sollten, wenn notwendig durch Aufspaltung von Profilsegmenten an Knotenpunkten des Kurses über Grund zur Einfügung von Querneigungswinkeländerungen. In der Regel ist die Länge des nächsten Segments zu Beginn unbekannt und wird unter Annahme eines unveränderten Querneigungswinkels mit einem Vorläufigkeitswert berechnet. Wird dann festgestellt, dass sich das vorläufige Segment über einen oder mehrere Kurs-über-Grund-Knotenpunkte erstreckt und der erste s ist, d. h. s1 < s < s2 , wird das Segment bei s abgeschnitten, und die Parameter dort werden durch Interpolation errechnet (siehe unten). Diese werden zu den Endpunktparametern des aktuellen Segments und zu den Anfangspunktparametern eines neuen Segments, das weiterhin über die gleichen Zielendbedingungen verfügt. Ist kein eingreifender Kurs-über-Grund-Knotenpunkt vorhanden, wird das vorläufige Segment bestätigt.
Sollen die Effekte von Kurven auf das Flugprofil außer Acht gelassen werden, kommt die Geradeausfluglösung mit einem einzigen Segment zur Anwendung; Informationen zum Querneigungswinkel werden für die Korrektur aufgrund der Triebwerksanbringung,Δ1 (Installationseffekt) festgehalten.
Eine dreidimensionale Flugbahn wird jeweils durch Zusammenfügen ihres zweidimensionalen Flugprofils und ihres zweidimensionalen Kurses über Grund generiert. Das Ergebnis ist eine Folge von Koordinatenpunkten (x, y, z), die entweder einen Knotenpunkt des segmentierten Kurses über Grund, einen Knotenpunkt des Flugprofils oder beides beschreiben. Dabei enthalten die Profilpunkte Angaben über die Höhe z, die Geschwindigkeit über GrundV, den Querneigungswinkelε und die TriebwerksleistungP. Für einen Streckenpunkt (x, y), der zwischen den Endpunkten eines Flugprofilsegments liegt, werden die Flugparameter wie folgt interpoliert:
| z = z1 + f (z2 - z1) , | ( 5) |
| V = √(V12 + f(V22 - V12) ), | ( 6) |
| ε = ε1 + f(ε2 - ε1) | ( 7) |
| P = √(P12 + f(P22 - P12)) , | ( 8) |
| wobei | |
| f = ((s - s1) / (s2 - s1)) | ( 9) |
z undε ändern sich linear mit der Entfernung,V undP linear mit der Zeit (d. h. konstante Beschleunigung 10).
ANMERKUNG: Beim Abgleich von Flugprofilsegmenten mit Radardaten (Flugbahnanalyse) werden alle Endpunktentfernungen, Höhen, Geschwindigkeiten und Querneigungswinkel direkt aus den Daten bestimmt; nur die Triebwerkseinstellungen müssen unter Anwendung der Leistungsrechnungen berechnet werden.
15.3 Teilsegmentierung der Startrollstrecke
Wenn das Luftfahrzeug beim Start zwischen dem Punkt, an dem die Bremsen gelöst werden (Brake Release Point, auch "Start-of-Roll-Punkt" (SOR) genannt), und dem Abhebepunkt beschleunigt, ändert sich die Geschwindigkeit erheblich über eine Strecke von 1.500 bis 2.500 m von null auf 80 bis 100 m/s.
Der Startrollstrecke wird daher in Teilsegmente mit veränderlicher Länge unterteilt, über die sich die Geschwindigkeit des Luftfahrzeugs um ein spezifisches Inkrement ΔV von höchstens 10 m/s ändert. Die Beschleunigung wird als konstant angenommen.
Dabei ist
| V1 | die Anfangsgeschwindigkeit, |
| V2 | die Startgeschwindigkeit, |
| nTO | die Anzahl der Teilsegmente und |
| sTO | die äquivalente Startstrecke (siehe Anhang B). |
Für die äquivalente StartstreckesTO, die AnfangsgeschwindigkeitV1. und die Start- bzw. EndgeschwindigkeitV2 beträgt die Anzahl der Teilsegmente für die Startrollstrecke
| nTO = int(1 + ((V2 -V1) / 10) . | ( 10) |
Somit ist die Geschwindigkeitsänderung entlang eines Teilsegments
| ΔV = ((V2 -V1) /nTO) | ( 11) |
und die Zeit Δt in jedem Teilsegment (unter Annahme einer konstanten Beschleunigung)
| Δt = (2STO / (V2 + V1)nTO) | ( 12) |
Die LängeSTO,k von Segmentk (1 ≤k ≤nTO) der Startrollstrecke ist also:
| STO,k = (V1 + ΔV (k - 0,5)) (2STO / (V2 +V1)nTO) | ( 13) |
BEISPIEL:
Bei einer StartstreckesTO = 1.600 m,V1= 0 m/s undV2 = 75 m/s ergeben sichnTO = 8"Teilsegmente" mit Längen von 25 bis 375 Metern (siehe Abbildung 7).
Abbildung 7: Teilsegmentierung einer Startrollstrecke; Beispiel für acht Teilsegmente
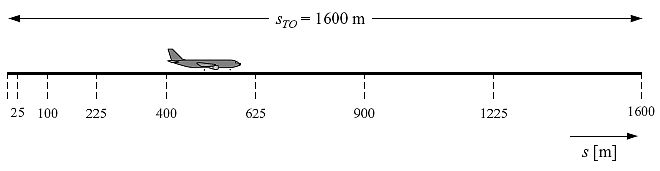
Analog zu den Geschwindigkeitsänderungen errechnen sich die Schubänderungen eines Luftfahrzeugs über jedes Teilsegment mit einem konstanten Inkrement ΔP als
| ΔP = (PTO -Pinit) /nTO | ( 14) |
Hierbei bezeichnenPTO undPinit den jeweiligen Schub am Abhebepunkt bzw. am Start-of-Roll-Punkt. Mit der Verwendung dieser konstanten Schubänderung soll Konsistenz mit dem linearen Verhältnis zwischen Schub und Geschwindigkeit bei Strahlflugzeugen hergestellt werden (Gleichung ( B.1)).
15.4 Teilsegmentierung der Anfangssteigflugsegmente und der Endanflugsegmente
Bei den Anfangssteigflugsegmenten und den Endanflugsegmenten ändert sich die Geometrie zwischen Segment und Immissionsort sehr rasch. Insbesondere bei Immissionsorten seitlich der Flugstrecke ändert sich derBeta-Winkel beim Steig- bzw. Landeflug schnell. Die Genauigkeit der Berechnung verbessert sich, wenn die Endanflug- bzw. Anfangssteigflugsegmente weiter zerlegt werden. Die Länge der einzelnen Teilsegmente (und folglich ihre Anzahl) richtet sich nach der festzusetzenden, maximalen Änderung der seitlichen Dämpfung. Für Luftfahrzeuge mit am Rumpf montierten Triebwerken lässt sich zeigen, dass sich die Änderung der seitlichen Dämpfung auf 1,5 dB je Teilsegment begrenzen lässt, wenn die Anfangssteigflug- und Endanflugsegmente unterhalb von 1.289,6 m (4.231 ft) auf Basis der folgenden Menge von Höhenwerten in Teilsegmente zerlegt werden:
z" = {18,9; 41,5; 68,3; 102,1; 147,5; 214,9; 334,9; 609,6; 1.289,6} Meter bzw.
z" = {62; 136; 224; 335; 484; 705; 1.099; 2.000; 4.231} Fuß.
ANMERKUNG: Die obengenannten Zahlenwerte sind gerundet, ggf. müssen bei der Umrechnung von Fuß in Meter (und umgekehrt) die signifikanten Nachkommastellen berücksichtigt werden, um übereinstimmende Ergebnisse zu erreichen.
Für jedes ursprüngliche Segment unterhalb von 1.289,6 m (4.231 ft) wird unter Verwendung der obigen Höhen geprüft, ob es in Teilsegmente zu zerlegen ist. Dazu wird für jede Endpunkthöhe der ursprünglichen Steig- bzw. Landesegmente zj die nächstgrößere Höhez"N aus der Menge der Höhenwerte bestimmt. Der Endpunkt eines Segments ist dabei der Punkt des Segments mit der größten Entfernung zum Bahnbezugspunkt entlang des Kurses über Grund unabhängig von der Flugrichtung. Die Teilsegmenthöhenzji werden dann wie folgt berechnet:
| zij = zj (z"i / z"N) (i =k ... N) . | ( 15) |
Dabei bezeichnet
| zj | die Endpunkthöhe des ursprünglichen Steig- bzw. Landesegments |
| z"j | das i-te Element aus der Menge von Höhenwerten |
| z"N | die nächstgrößere Höhe aus der Menge der Höhenwerte zur Höhe |
| k | den Wert des Indexi, bei dem die errechnete Teilsegmenthöhe zjk erstmalig größer ist als die Endpunkthöhe des (beim Abflug in Flugrichtung und beim Anflug entgegen der Flugrichtung) vorhergehenden, ursprünglichen Segmentszj-1; d.h.zj-1 < zjk |
Dieses Verfahren führt dazu, dass die Änderung der seitlichen Dämpfung je Teilsegment annähernd konstant bleibt und genauere Konturen ergibt, ohne dass sehr kurze Segmente verwendet werden müssen.
Falls die ursprüngliche Endpunkthöhe eines Steigflugsegments bzw. die Startpunkthöhe eines Anflugsegments größer als 1.289,6 m (4.231 ft) ist, ist Gleichung (15) mitzj = 1289,6 m zu verwenden.
BEISPIEL:
Liegt die Endpunkthöhe des j-ten Originalsegments beizj = 304,8 m, dann ist aus der Menge der Höhenwerte 214,9 < 304,8 < 334,9 die zuzj = 304,8 m nächstgrößere Höhez"7 = 334,9 m. Die Endpunkthöhen der Teilsegmente werden dann berechnet mit:
zji = 304,8 (zi / 334,9) (i = 1 ... 7) .
Es ergibt sich alsozj1 = 17,2 m,zj2 = 37,8 m usw. für den Fall, dasszj-1 < 17,2 m.
Die Geschwindigkeits- und Triebwerksleistungswerte an den eingeschobenen Punkten werden unter Verwendung der Gleichungen ( 6) beziehungsweise ( 8) interpoliert.
15.5 Teilsegmentierung von Flugsegmenten
Neben der Teilsegmentierung der Startrollstrecke und des Anfangssteigflugs bzw. des Endanflugs können weitere Segmentierungsanpassungen notwendig sein. Dazu gehören
Wenn benachbarte Punkte weniger als 10 m voneinander entfernt liegen und die dazugehörigen Geschwindigkeits- und Schubwerte gleich sind, ist einer der Punkte zu entfernen. Bei Flugsegmenten mit erheblicher Geschwindigkeitsänderung entlang eines Segments erfolgt eine Unterteilung wie bei der Startrollstrecke, d. h.
| nseg = int (1 + (|Vj+1 -Vj| / 10) , | ( 16) |
wobei
| Vj | die Geschwindigkeit am Anfangspunkt des Segments und |
| Vj+1 | die Geschwindigkeit am Endpunkt des Segments. |
Die entsprechenden Teilsegmentparameter werden in gleicher Weise wie bei der Startrollstrecke unter Verwendung der Gleichungen ( 11) bis (13) berechnet.
15.6 Das Landerollen
In den für Deutschland geltenden Fixpunktprofilen aus der BUF-D ist die Schubumkehr bereits berücksichtigt. Diese Fixpunktprofile sind grundsätzlich zu verwenden. Weichen flugbetriebliche Parameter, wie in der BUF-D beschrieben, von den Standardparametern ab, sollten der Flugbetriebssituation entsprechende Profile berechnet werden.
Dabei ist beim Landerollen die Schubumkehr zu berücksichtigen, wenn diese genutzt wird.
Im Gegensatz zur Startrollstrecke, die aus den Luftfahrzeugleistungsparametern hergeleitet wird, ist die Landerollstreckesstop (d. h. die Strecke vom Aufsetzpunkt bis zu dem Punkt, an dem das Luftfahrzeug die Landebahn verlässt) nicht nur luftfahrzeugspezifisch. Sie hängt darüber hinaus auch von der Lage der Rollbahnen, der Verkehrslage sowie von flugplatzspezifischen Regelungen über den Einsatz des Umkehrschubs ab.
Der Einsatz der Schubumkehr ist kein Standardverfahren. Sie kommt nur zur Anwendung, wenn das notwendige Abbremsen nicht mithilfe der Radbremsen erreicht werden kann.
Physikalisch ist der Schubumkehrlärm ein sehr komplexer Prozess, der sich grob vereinfachend modellieren lässt, indem der rasche Wechsel der Triebwerksleistung durch eine geeignete Segmentierung berücksichtigt wird.
Die folgenden vereinfachten Modellierungsannahmen sind anzuwenden, wenn keine detaillierten Informationen zur Verfügung stehen (siehe Abbildung 8).
Abbildung 8: Die Grafik macht die prinzipiellen Abläufe deutlich, sie dient nicht zur Berechnung der Teilsegmente beim Landerollen.
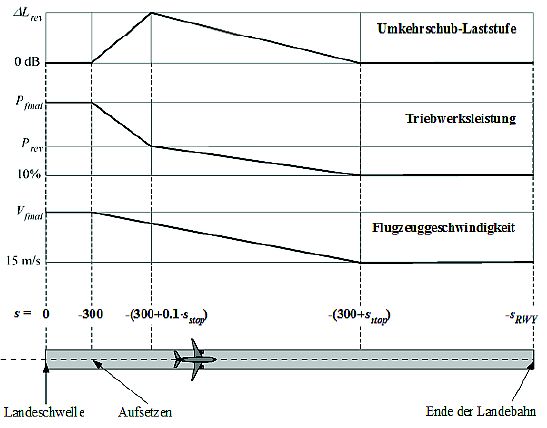
15.7 Modellierung des Landerollens
Das Luftfahrzeug setzt 300 m hinter der Landeschwelle (Koordinate s = 0 im Anflugkurs über Grund) auf (siehe Abbildung 8). Anschließend wird das Luftfahrzeug über eine Landerollstreckesstop - luftfahrzeugspezifische Werte dafür enthält die BUF-D - von der EndanfluggeschwindigkeitVfinal auf 15 m/s abgebremst. Aufgrund der raschen Geschwindigkeitsänderungen in diesem Segment wird es mithilfe der Gleichungen ( 10) bis (13) ebenso in Teilsegmente zerlegt wie beim Startrollen (oder bei Flugsegmenten mit betragsmäßig größeren Beschleunigungen).
ANMERKUNG: Die Triebwerksleistung ändert sich von der Endanflugleistung beim Aufsetzen zur SchubumkehreinstellungPrev über eine Strecke 0,1 *sstop und verringert sich dann über die restlichen 90 % der Ausrollstrecke auf 10 % der verfügbaren Volllast. Bis zum Ende der Landebahn (beis = -sRWY) bleibt die Fluggeschwindigkeit konstant. Typischerweise ist die SchubumkehrleistungPrev etwa 20 % der Volllasteinstellung. Dieser Wert ist anzusetzen, wenn keine Betriebsinformationen verfügbar sind. Bei einer bestimmten Leistungseinstellung erzeugt die Schubumkehr jedoch tendenziell mehr Lärm als der Vorwärtsschub, so dass auf den NPD-hergeleiteten Ereigniswert ein Inkrement ΔL anzuwenden ist, das entlang 0,1 ·sstop von null auf einen Wert ΔLrev von 5 dB steigt und danach über die verbleibende Ausrollstrecke linear auf null sinkt.
15.8 Platzrunde
Platzrunden werden in Abflug-, Horizontalflug- und Anflugteil gegliedert. Die Streckenbeschreibung von Platzrunden ist zum einen geometrisch geschlossen und weist zum anderen eine Kursänderung von insgesamt 360 Grad auf.
16 Lärmberechnung für ein Einzelereignis
Den Kern des Modellierungsprozesses bildet die Berechnung des Schallexpositionspegels aus den in den Abschnitten 9 bis 15 beschriebenen Flugbahninformationen.
17 Einzelereignismaß
Der von einer Flugbewegung am Immissionsort empfangene Schall wird durch den Schallexpositionspegel charakterisiert. In diesem Dokument werden nur A-bewertete Lärmindizes betrachtet. Die Kennzeichnung der Skala erfolgt in der Regel durch eine entsprechende Indexerweiterung, z.B.LpAE ,LpAmax .
Der A-bewertete Schallexpositionspegel wird mit Hilfe der Schallexposition
 |
( 17) |
| ausgedrückt als | |
| LpAE = 10 lg (EA / EO) . | ( 18) |
Eo bezeichnet die Bezugsschallexposition, welche durch das Produkt aus dem Quadrat des Bezugsschalldrucks und der Bezugsdauer von 1 s gegeben ist. Mit der Wahl des Integrationsintervalls [t1,t2] soll sichergestellt werden, dass nahezu der gesamte signifikante Schall im Ereignis erfasst ist. Die Integrationsgrenzen t1 und t2 werden so gewählt, dass der SchalldruckpegelL (t) im Zeitintervall [t1,t2] nicht mehr als 10 dB unterhalb vonLpmax liegt. Diese Spanne wird als "10-dB-down-time" bezeichnet. Schallexpositionspegel in den Tabellen der BUF-D sind 10-dB-down-time-Werte 11.
In der Praxis wird der Schallexpositionspegel in Annäherung an Gleichung ( 18) aus dem zeitabhängigen (zeitbewerteten) SchalldruckpegelLpA (t) bestimmt:
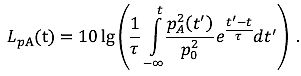 |
( 19) |
| Mit diesem ergibt sich der Schallexpositionspegel LpAE zu: | |
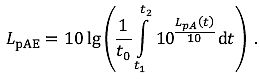 |
( 20) |
Gleichung ( 20) kann zur Bestimmung von Schallexpositionspegeln verwendet werden, wenn der gesamte ZeitverlaufLpA(t) bekannt ist.
Da eine Flugbahn und ihre Parameter aber durch diskrete Werte gegeben sind, erfolgt die Berechnung des Schallexpositionspegels durch Addition von Segmentwerten, deren jeweilige Segmentexpositionspegel dem Beitrag eines einzelnen endlichen Segments der Flugbahn entsprechen:
 |
( 21) |
18 Bestimmung von Maximal- und Schallexpositionspegeln anhand von NPD-Daten
Die Hauptquelle für Fluglärmdaten ist die BUF-D, die Daten aus der internationalen Aircraft Noise and Performance Database (ANP-Datenbank) enthält. Darin sind die BasispegelLpAmax (P, d) undLpAE∞ (P, d) als Funktionen des kürzesten Abstands vom Immissionsort zu einem Flugbahnsegmentd für spezifische Luftfahrzeugmuster, -varianten, Luftfahrzeugkonfigurationen (Anflug, Abflug, Klappenstellungen) und LeistungseinstellungenP tabellarisch aufgeführt. Sie beziehen sich auf einen stationären Flug bei der ReferenzgeschwindigkeitVref auf einer theoretisch unendlichen, geraden Flugbahn 12.
Aus den Tabellen 10 oder 16 der BUF-D erhält man aus den EingabewertenP undd die gesuchten BasispegelLpAmax (P, d) und/oderLpAE∞ (P, d) (anwendbar auf eine unendliche Flugbahn).LpAmax (P, d) ist der NPD-Maximalpegel eines Segments in der kleinsten Entfernung d vom Segment zum Immissionsort. Der größte aller SegmentpegelLpAmax (P, d) ist unter Berücksichtigung desInstallationseffekts Δ1(Φ) und der SeitlichenDämpfung Λ(β, ) auch der MaximalpegelLpAmax des Ereignisses. Sollten in der NPD-Tabelle keine genauen Werte fürP und/oderd angegeben sein, sind die benötigten Werte zu interpolieren. Dabei kommt zwischen tabellarisierten Leistungseinstellungen eine lineare Interpolation und zwischen tabellarisierten Abständen eine logarithmische Interpolation zur Anwendung (siehe Abbildung 9).
) auch der MaximalpegelLpAmax des Ereignisses. Sollten in der NPD-Tabelle keine genauen Werte fürP und/oderd angegeben sein, sind die benötigten Werte zu interpolieren. Dabei kommt zwischen tabellarisierten Leistungseinstellungen eine lineare Interpolation und zwischen tabellarisierten Abständen eine logarithmische Interpolation zur Anwendung (siehe Abbildung 9).
Abbildung 9: Interpolation bei Lärm-Leistung-Abstand-Kurven (NPD-Kurven), auf der Abszisse ist der Schrägabstand (logarithmische Skala) aufgetragen
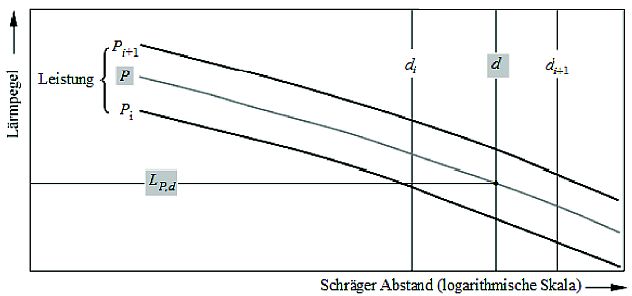
Nachstehend wird jede Art von Lärmpegel (z.B. Maximal- oder Schallexpositionspegel) verallgemeinernd mitL(P) beschrieben. WennPi undPi+1 Triebwerksleistungswerte sind, für die Lärmpegel zu Abstandsdaten tabellarisiert sind, errechnet sich der LärmpegelL(P) in einem bestimmten Abstand für die mittlere LeistungP zwischenPi undPi+1 wie folgt:
| L(P) =L(Pi) + [ (L(Pi+1) -L(Pi)) / (Pi+1 - Pi) ] (P - Pi) . | ( 22) |
Wenn bei einer beliebigen Leistungseinstellungdi unddi+1 Abstände sind, für die Lärmdaten tabellarisiert sind, errechnet sich der LärmpegelL(d) für einen mittleren Abstandd zwischendi unddzi+1 wie folgt:
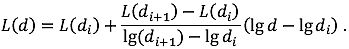 |
( 23) |
Mit den Gleichungen ( 22) und ( 23) lässt sich ein LärmpegelL(P, d) für eine beliebige LeistungseinstellungP und einen beliebigen Abstandd errechnen, der innerhalb des Rahmens der NPD-Tabellen liegt.
Für Abständed außerhalb des NPD-Rahmens wird Gleichung ( 23) verwendet, um von den letzten beiden Werten zu extrapolieren, d. h. nach innen vonL(d1) undL(d2) oder nach außen vonL(di-1) undL(d1). Dabei bezeichnetI die Gesamtzahl der NPD-Punkte.
Somit ergibt sich:
Ergibt sich fürd ein Wert < 30 m , so wirdd = 30 m gesetzt.
18.1 Impedanzanpassung von Standard-NPD-Daten
Die in der BUF-D angegebenen NPD-Daten sind auf spezifische atmosphärische Bedingungen normalisiert (Temperatur 25 °C und Druck 1.013,25 hPa). Vor Anwendung der oben beschriebenen Interpolations-/Extrapolationsmethode ist für diese Daten eine akustische Impedanzanpassung vorzunehmen.
ANMERKUNG: Die akustische Impedanz bezieht sich auf die Ausbreitung von Schallwellen in einem akustischen Medium und ist definiert als Produkt aus Luftdichte und Schallgeschwindigkeit. Bei einer in einem bestimmten Abstand von der Quelle empfangenen Schallintensität (Schallleistung je Flächeneinheit) hängt der damit zusammenhängende Schalldruck (zur Definition der Maße SEL undLpAmax) von der akustischen Impedanz der Luft am Messort ab. Er ist eine Funktion der Temperatur, des Luftdrucks und indirekt der Höhe. Daher müssen die Standard-NPD-Daten der BUF-D so angepasst werden, dass Temperatur und Druckbedingungen in ihren tatsächlichen Werten berücksichtigt werden, die sich im Allgemeinen von den normalisierten Bedingungen der Daten in der BUF-D unterscheiden.
Die auf die Standard-NPD-Pegel anzuwendende Impedanzanpassung wird wie folgt ausgedrückt:
| Δimpedance = 10 lg (ρ · c / 409,81) . | ( 26) |
Dabei gilt Folgendes:
| Δimpedance | Impedanzanpassung zur Berücksichtigung der tatsächlichen atmosphärischen Bedingungen am Immissionsort (dB) |
| ρ · c | Akustische Impedanz der Luft am Immissionsort |
| 409,81 | Akustische Impedanz der Luft bezogen auf die atmosphärischen Referenzbedingungen der NPD-Daten (Zo = 409,81 Ns/m3) |
Die Impedanzρ · c wird wie folgt berechnet:
| ρ · c = 416,86(δ / √θ) . | ( 27) |
Dabei gilt Folgendes:
| δ | δ =p/po , Verhältnis des Umgebungsluftdrucks auf Immissionsorthöhe zum Standardluftdruck auf Meereshöhe:po = 1.013,25 hPa (oder 1.013,25 mb) |
| θ | θ = (T + 273,15)/(To + 273,15) , Verhältnis der Jahresdurchschnittslufttemperatur auf Immissionsorthöhe zur Standardlufttemperatur auf Meereshöhe:To = 15,0 °C |
ANMERKUNG: Die akustische Impedanzanpassung beträgt in der Regel weniger als einige Zehntel dB. Es sei insbesondere darauf hingewiesen, dass unter den atmosphärischen Standardbedingungen (po = 1.013,25 hPa undTo = 15,0 °C) die Impedanzanpassung weniger als 0,1 dB (0,074 dB) beträgt. Bei einer signifikanten Abweichung der Temperatur und des Luftdrucks gegenüber den atmosphärischen Referenzbedingungen der NPD-Daten kann die Anpassung jedoch erheblicher sein.
19 Allgemeine Ausdrücke
19.1 Segmentpegel
Die Bestimmung der Segmentwerte erfolgt durch Anpassung der Basiswerte (unendliche Flugbahn) gemäß NPD-Daten. Der maximale Schalldruckpegel eines FlugbahnsegmentsLpAmax,seg lässt sich im Allgemeinen ausdrücken als
LpAmax,seg =LpAmax(P, d) + Δl (Φ) - Λ(β, ) ) |
( 28) |
und der Beitrag eines Flugbahnsegments zu LmE als
LpAE,seg =LpAE∞ (Δ) + ΔV + Δl (9) - Λ(β, ) + ΔF . ) + ΔF . |
( 29) |
Die "Korrekturterme" in den Gleichungen ( 28) und ( 29), die in Abschnitt 21 ausführlich beschrieben werden, berücksichtigen die folgenden Effekte:
| ΔV | Dauer-Korrektur: Die NPD-Daten beziehen sich auf eine Referenzfluggeschwindigkeit. Mit diesem Korrekturterm werden die Expositionspegel an Nichtreferenzgeschwindigkeiten angepasst. (Wird nicht aufLpAmax,seg angewendet.) |
| Δl(Φ) | Installationseffekt: beschreibt eine Änderung der lateralen Richtwirkung aufgrund einer von der Luftfahrzeugzelle, den Triebwerken und umgebenden Strömungsfeldern bewirkten Abschirmung, Brechung oder Reflexion. |
Δ(β, ) ) |
Seitliche Dämpfung: signifikant für Schall, der sich in kleinen Winkeln zum Boden hin ausbreitet. Berücksichtigt die Wechselwirkung zwischen direkten und reflektierten Schallwellen (Bodeneffekt) sowie die Effekte (in erster Linie vom Boden verursachter) atmosphärischer Ungleichmäßigkeiten, die Schallwellen auf deren Weg zum Immissionsort seitlich der Flugbahn brechen. |
| ΔF | Segmentkorrektur (Noise Fraction): berücksichtigt die endliche Länge des Segments gegenüber einer unendlich langen Flugbahn. Wird nur auf Expositionsmaße angewandt. |
Ist das Segment Teil der Startrollstecke oder der Landerollstrecke und befindet sich der Immissionsort hinter dem betreffenden Segment, so wird die ausgeprägte Richtcharakteristik von Strahltriebwerkslärm, die hinter einem startbereiten Luftfahrzeug auftritt, durch die Richtcharakteristikkorrektur ΔSOR und die besondere Form der Segmentkorrektur Δ"F für den Schallexpositionspegel berücksichtigt:
LpAmax,seg =LpAmax(P, d) + Δl(Φ) - Λ(β, ) + ΔSOR ) + ΔSOR |
( 30) |
LpAE,seg =LpAE∞ (P, d) + ΔV + ΔI(e) - Λ(β, ) + Δ"F + ΔSOR . ) + Δ"F + ΔSOR . |
( 31) |
Dabei gilt Folgendes:
| Δ"F | Besondere Form der Segmentkorrektur |
| ΔSOR | Richtcharakteristikkorrektur: zur Berücksichtigung der ausgeprägten Richtcharakteristik von Strahltriebwerkslärm hinter dem An- bzw. Abrollsegment. |
Die spezifische Behandlung der An- und Abrollsegmente wird in Abschnitt 21 beschrieben.
Die nachfolgenden Abschnitte beschreiben die Berechnung von Segmentschallpegeln.
19.2 EreignislärmpegelLpA einer Flugbewegung
Der MaximalpegelLpAmax ist der größte der Segmentwerte LpAmax,seg (Siehe Gleichungen ( 28) und ( 30)):
| LpAmax = max (LpAmax,seg) . | ( 32) |
Dabei wird jeder Segmentwert anhand der Luftfahrzeug-NPD-Daten für die LeistungP und den Abstandd bestimmt.
Der ExpositionspegelLpAE wird als logarithmische Summe der BeiträgeLpAgseg jedes lärmerheblichen Segments seiner Flugbahn berechnet:
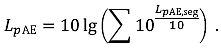 |
( 33) |
Die Addition verläuft über alle Flugbahnsegmente.
20 Flugbahnsegmentparameter
Die Bestimmung der LeistungP und des Abstandsd, für die die BasispegelLpAmax(P, d) undLpAE∞ (P, d) aus den NPD-Tabellen interpoliert werden, erfolgt anhand von geometrischen und betrieblichen Parametern, die das Segment definieren. Im Folgenden bezeichnet der Index "1" immer den Startpunkt eines Segments und der Index "2" den Endpunkt eines Segments. Die Indizes der Segmentpunkte werden wie die Entfernung über Grund beim Abflug in Flugrichtung und beim Anflug entgegen der Flugrichtung gezählt. Daher weist die Flugrichtung beim Abflug von S1 nach S2 und beim Anflug von S2 nach S1.
20.1 Geometrische Parameter für NPD-Basispegel
Die nächsten Abbildungen zeigen die Geometrien zwischen Quelle und Immissionsort, wenn sich der Immissionsort O hinter (Abbildung 10), neben (Abbildung 11) oder vor (Abbildung 12) dem Segment S1S2 befindet, wobei die Flugrichtung von S1 nach S2 weist (Abflug). (Beim Anflug müssen die Indizes "1" und "2" in Abbildung 10, Abbildung 11 und Abbildung 12 vertauscht werden und der Abstandsvektor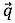 zeigt dann von Sp auf S2.) In diesen Abbildungen gilt Folgendes:
zeigt dann von Sp auf S2.) In diesen Abbildungen gilt Folgendes:
| O | ist der Immissionsort; |
| S1, S2 | sind der Startpunkt und der Endpunkt des Segments; |
| Sp | ist der Punkt des kleinsten Vorbeiflugabstands rechtwinklig zum Immissionsort für das Segment oder dessen Verlängerung; |
| d1,d2 | sind die Abstände zwischen dem Startpunkt bzw. Endpunkt des Segments und dem Immissionsort; |
| ds | ist der kürzeste Abstand zwischen Immissionsort und Segment; |
| dp | ist der senkrechte Abstand zwischen Immissionsort und verlängertem Segment (Schrägabstand); |
| λ | ist die Länge des Flugbahnsegments; |
| q | ist der Abstand von S1 zu Sp (bzw. von Sp zu S2 beim Anflug); negativ, wenn sich der Immissionsort hinter dem Segment befindet. |
Abbildung 10: Flugbahnsegmentgeometrie bei hinter dem Segment befindlichem Immissionsort
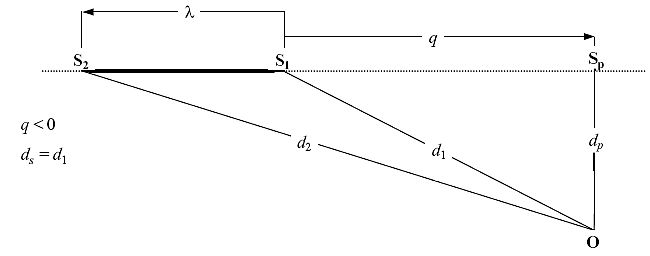
Abbildung 11: Flugbahnsegmentgeometrie bei neben dem Segment befindlichem Immissionsort
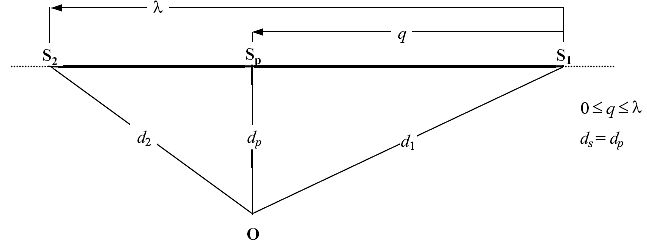
Abbildung 12: Flugbahnsegmentgeometrie bei vor dem Segment befindlichem Immissionsort
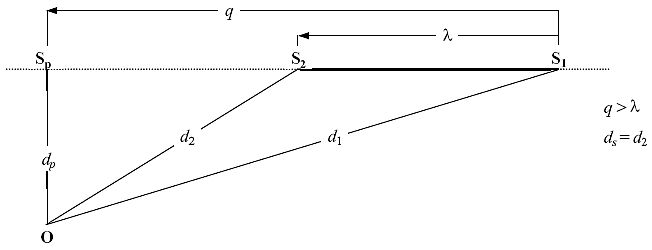
Das Flugbahnsegment ist durch eine dicke durchgehende Linie dargestellt. Die gepunktete Linie stellt dieFlugbahnverlängerung dar, die sich in beiden Richtungen ins Unendliche erstreckt. Für den ExpositionspegelLpAE ist der NPD-Abstandsparameterd gegeben durch den Abstanddp zwischen Sp und dem Immissionsort, genanntSchrägabstand.
Bei Expositionspegelmaßen, bei denen sich die Immissionsorte hinter den Bodensegmenten während des Startrollens bzw. vor den Bodensegmenten während des Landerollens befinden, wird jedoch der NPD-Abstandsparameterd zum Abstandd1 , dem kürzesten Abstand zwischen Immissionsort und Segment.
Bei Maximalpegelmaßen ist der NPD-Abstandsparameterd gegeben durchds , den kürzesten Abstand zwischen Immissionsort und Segment.
20.2 SegmentleistungP
Die tabellarisierten NPD-Daten beschreiben den Lärm eines Luftfahrzeugs im stationären Geradeausflug auf einer unendlichen Flugbahn, d. h. bei konstanter TriebwerksleistungP. Dementsprechend werden tatsächliche Flugbahnen, auf denen Geschwindigkeit und Richtung variieren, in eine Anzahl endlicher Segmente unterteilt. Diese sind jeweils als Teil einer einheitlichen unendlichen Flugbahn zu betrachten, für die die NPD-Daten gültig sind. Um Leistungsänderungen entlang eines Segments zu berücksichtigen, wird angenommen, dass sie sich linear mit zunehmendem Abstand vonP1 am Anfang zuP2 am Ende des Segments ändern. Daher muss ein äquivalenter stationärer SegmentwertP definiert werden. Dieser wird als Wert an dem Punkt des Segments angenommen, der dem Immissionsort am nächsten liegt. Befindet sich der Immissionsort längs des Segments (Abbildung 11), errechnet sich der Wert durch Interpolation gemäß Gleichung (8) zwischen Anfangs- und Endwert, d. h.
| P = √[p12 + (q/λ) (p22 - p12)] . | ( 34) |
Befindet sich der Immissionsort hinter oder vor dem Segment, ist der Wert derjenige am nächstgelegenen EndpunktP1 oderP2 .
21 Korrekturterme für Segmentpegel
Die NPD-Daten definieren Maximal- und Schallexpositionspegel als Funktion des Abstands senkrecht unterhalb einer idealisierten stationären Geradeausflugbahn unendlicher Länge, auf der sich das Luftfahrzeug mit stationärer Leistung bei einer festen Referenzgeschwindigkeit bewegt 13. Der anhand der NPD-Tabelle für eine spezifische Leistungseinstellung und einen bestimmten Schrägabstand interpolierte Maximal- bzw. Schallexpositionspegel wird somit alsBasispegel beschrieben. Er gilt für eine unendliche Flugbahn und muss korrigiert werden (siehe Gleichungen ( 28) und ( 29)) zur Berücksichtigung:
21.1 Dauerkorrektur ΔV (nur ExpositionspegelLpAE)
Um Abweichungen der jeweiligen Segmentgeschwindigkeit von der FlugreferenzgeschwindigkeitVref , auf die sich die NPD-Basisdaten beziehen, zu berücksichtigen, wird auf Expositionspegel die Dauerkorrektur 14 angewendet. Wie die Triebwerksleistung schwankt auch die Geschwindigkeit entlang des Segments von VT1 zu VT2 (hierbei ist die TAS den Fixpunktprofilen zu entnehmen), so dass eine äquivalente SegmentgeschwindigkeitVseg bestimmt werden muss.
Für Flugsegmente istVseg die Geschwindigkeit am Punkt des kleinsten Vorbeiflugabstands S. Befindet sich der Immissionsort hinter oder vor dem Segment, ist der Wert derjenige am nächstgelegenen Endpunkt VT1 oder VT2 .
Wenn sich der Immissionsort neben dem Segment befindet, wird zwischen den Segmentendpunktwerten wie folgt interpoliert:
 |
( 35) |
Für Segmente der Start-/Landebahn (Teile der Startrollstrecke oder der Landerollstrecke) wirdVseg als Durchschnitt der Segmentanfangs- und -endgeschwindigkeit angenommen, d. h.
| Vseg =(VT1 +VT2) / 2 . | ( 36) |
In beiden Fällen beträgt die additive Dauerkorrektur somit
| ΔV = 10 lg (Vref /Vseg) | ( 37) |
21.2 Geometrie der Schallausbreitung
Abbildung 13 zeigt beispielhaft für den Installationseffekt die Basisgeometrie in der Ebene senkrecht zur Flugbahn des Luftfahrzeugs. Die Grundlinie ist der Schnittpunkt zwischen der senkrechten Ebene und der Grundebene. Verläuft die Flugbahn waagerecht, ist die Grundlinie eine Seitenansicht der Grundebene. Das Luftfahrzeug ist im Winkelε, gemessen entgegen dem Uhrzeigersinn, um seine Längsachse quergeneigt. Der Winkelε ist somit bei Linkskurven positiv und bei Rechtskurven negativ.
Abbildung 13: Winkel zwischen Luftfahrzeug und Immissionsort in der Ebene senkrecht zur Flugbahn
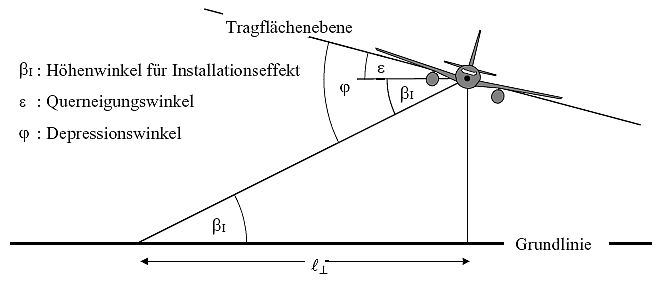
DerHöhenwinkelβ1 (zwischen 0 und 90°) ist gegeben als Winkel zwischen Schrägabstanddp, dem kürzesten Abstand vom Immissionsort zum verlängerten Segment, und seitlichem Versatz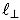 , dem senkrechten Abstand zwischen Immissionsort und der senkrecht auf die Grundebene projizierten Segmentverlängerung. Bei der Berechnung der seitlichen Dämpfung wird der Höhenwinkelβ beim Schallexpositionspegel auf die gleiche Weise ermittelt, allerdings in Bezug auf eine äquivalente, horizontale Flugbahn. Bei der seitlichen Dämpfung hinsichtlich des Maximalpegels ergibt sichβ als Winkel zwischend, dem kürzestem Abstand zwischen Immissionsort und einem Punkt des Segments und
, dem senkrechten Abstand zwischen Immissionsort und der senkrecht auf die Grundebene projizierten Segmentverlängerung. Bei der Berechnung der seitlichen Dämpfung wird der Höhenwinkelβ beim Schallexpositionspegel auf die gleiche Weise ermittelt, allerdings in Bezug auf eine äquivalente, horizontale Flugbahn. Bei der seitlichen Dämpfung hinsichtlich des Maximalpegels ergibt sichβ als Winkel zwischend, dem kürzestem Abstand zwischen Immissionsort und einem Punkt des Segments und *, dem Abstand zwischen Immissionsort und der senkrechten Projektion dieses Punktes auf die Grundebene (bei Segmenten vor oder hinter dem Immissionsort) bzw.
*, dem Abstand zwischen Immissionsort und der senkrechten Projektion dieses Punktes auf die Grundebene (bei Segmenten vor oder hinter dem Immissionsort) bzw.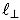 (wenn sich das Segment neben dem Immissionsort befindet). Der seitliche Versatz
(wenn sich das Segment neben dem Immissionsort befindet). Der seitliche Versatz wird also entweder aus
wird also entweder aus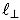 bzw. aus
bzw. aus * bestimmt. . Dies wird ausführlich erläutert in 21.5.
* bestimmt. . Dies wird ausführlich erläutert in 21.5.
DerDepressionswinkel Φ zwischen der Tragflächenebene und dem Ausbreitungsweg bestimmt die Triebwerksanbringungseffekte. In Bezug auf die Konvention für den Querneigungswinkel istΦ =βl ±ε mit positivem Vorzeichen bei Immissionsorten Steuerbord (rechts) und negativem Vorzeichen bei Immissionsorten Backbord (links).
21.3 Korrektur aufgrund der Triebwerksanbringung Δ1
Ein überfliegendes Luftfahrzeug ist eine vielschichtige Schallquelle. Dabei kommt zu dem Umstand, dass sich die Triebwerke und die Luftfahrzeugzelle als komplexe Ursprungsquellen erweisen, hinzu, dass auch die Zellenkonfiguration und insbesondere die Lage der Triebwerke die Schallabstrahlung beeinflussen. Dies führt zu einer uneinheitlichen Richtwirkung des seitlich um die Längsachse des Luftfahrzeugs abgestrahlten Schalls, was hier alslaterale Richtcharakteristik bezeichnet wird.
Hinsichtlich der lateralen Richtcharakteristik bestehen zwischen Luftfahrzeugen mit am Rumpf montierten Triebwerken und solchen, bei denen die Triebwerke unter den Tragflächen angebracht sind, signifikante Unterschiede, die im folgenden Ausdruck berücksichtigt werden:
| Δ1(Φ) = 10 lg[(a cos2 Φ + sin2Φ)b / (c sin2 2Φ + cos2 2Φ)] | ( 38) |
Dabei gilt Folgendes:
| Δ1(Φ) | Korrektur in dB beim DepressionswinkelΦ (siehe Abbildung 13) |
| a, b, c | bei Triebwerken unterhalb der Tragflächen:
a = 0,00384, b = 0,0621, c = 0,8786 bei Triebwerken am Rumpf: a = 0,1225, b = 0,3290, c = 1 |
Bei Propellerflugzeugen sind die Unterschiede der Richtwirkung vernachlässigbar, so dass gilt
| Δ1(Φ) = 0. | ( 39) |
Abbildung 14 zeigt die Abweichung von Δ1(Φ) um die Längsachse des Luftfahrzeugs für drei Triebwerksanbringungsarten. Bei negativemΦ wird für alle Anbringungsarten Δ1 (Φ) = Δ1 (0) verwendet.
Abbildung 14: Laterale Richtcharakteristik von Installationseffekten
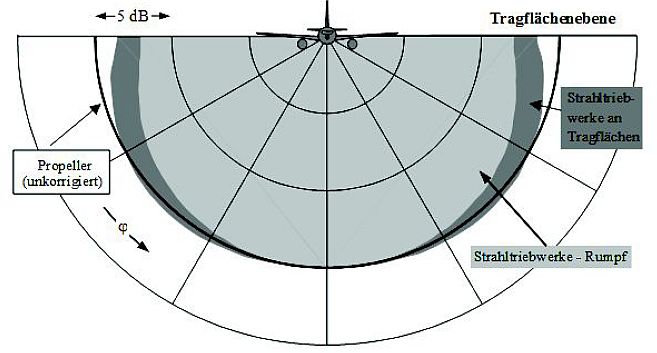
Es wird angenommen, dass die Korrektur Δ1(Φ) zweidimensional ist, d. h. sie ändert sich nicht mit dem Längsabstand zwischen Immissionsort und Luftfahrzeug. Somit wird derHöhenwinkel β1 für Δ1(Φ) definiert als β1 = arccos( /dp) .
/dp) .
21.4 Seitliche Dämpfung Λ ( β , ) (unendliche Flugbahn)
) (unendliche Flugbahn)
Die tabellarisierten NPD-Maximal- und Schallexpositionspegel beziehen sich auf einen stationären Horizontalflug und beruhen auf Messungen in 1,2 m Höhe über weichem, ebenem Grund unterhalb des Luftfahrzeugs.
Seitlich der Flugbahn ist der Abstandsparameter der Schrägabstand - die Länge der Senkrechten vom Immissionsort zur Flugbahn.
ANMERKUNG: An jeder seitlichen Position ist der Lärmpegel generell geringer als im gleichen Abstand unmittelbar unterhalb des Luftfahrzeugs. Neben derlateralen Richtcharakteristik oder den "Installationseffekten", wie sie oben beschrieben wurden, ist dies auf eine übermäßigeseitliche Dämpfung zurückzuführen. Diese bewirkt, dass der Schallpegel mit zunehmendem Abstand schneller sinkt als in den NPD-Kurven angegeben. Es wird die folgende Methodik zur Berechnung der seitlichen Dämpfung empfohlen. Sie ist beschränkt auf den Fall der Schallausbreitung über weichem ebenem Grund, was für die große Mehrheit von Zivilflugplätzen geeignet ist. Anpassungen an die Effekte einer harten Bodenoberfläche (oder, akustisch äquivalent, von Wasser) befinden sich noch in der Entwicklung.
Diese Methodik baut auf dem umfangreichen Bestand an Experimentaldaten zur Schallausbreitung von Luftfahrzeugen mit am Rumpf montierten Triebwerken im stationären horizontalen Geradeausflug auf. Unter der Annahme, dass im Horizontalflug die Luft-Boden-Dämpfung
 abhängt,
abhängt,wurden die Daten analysiert, so dass sich eine empirische Funktion für die seitliche Gesamtanpassung ΛT(β, ) (= seitlicher Ereignispegel minus Pegel im gleichen Abstand unterhalb des Luftfahrzeugs) ergibt. Da der Term ΛT(β,
) (= seitlicher Ereignispegel minus Pegel im gleichen Abstand unterhalb des Luftfahrzeugs) ergibt. Da der Term ΛT(β, ) sowohl die laterale Richtcharakteristik als auch die seitliche Dämpfung berücksichtigt, kann die seitliche Dämpfung durch Subtraktion extrahiert werden.
) sowohl die laterale Richtcharakteristik als auch die seitliche Dämpfung berücksichtigt, kann die seitliche Dämpfung durch Subtraktion extrahiert werden.
Bei Beschreibung der lateralen Richtcharakteristik durch Gleichung ( 38) mit den Rumpfmontagekoeffizienten und unter Ersetzung vonΦ durchβ für Geradeausflug, wird die seitliche Dämpfung zu:
Λ(β, ) = ΛT(β, ) = ΛT(β, ) Λ1(β) . ) Λ1(β) . |
( 40) |
Dabei erfolgt die Messung vonβ und wie in Abbildung 13 dargestellt, in einer Ebene senkrecht zur unendlichen Flugbahn, die bei Horizontalflug (β =β1) auch vertikal ist.
wie in Abbildung 13 dargestellt, in einer Ebene senkrecht zur unendlichen Flugbahn, die bei Horizontalflug (β =β1) auch vertikal ist.
Die seitliche Dämpfung Λ(β, ) lässt sich approximieren durch
) lässt sich approximieren durch
Λ(β, ) = Γ ) = Γ · Λ(β) . · Λ(β) . |
( 41) |
Dabei ist Γ( ) ein Abstandsfaktor, gegeben durch
) ein Abstandsfaktor, gegeben durch
Γ( ) = 1,089[1 - exp(-0,00274 ) = 1,089[1 - exp(-0,00274 )] für 0≤ )] für 0≤ ≤ 914 m , ≤ 914 m , |
( 42) |
Γ( ) = 1 für ) = 1 für > 914 m , > 914 m , |
( 43) |
und Λ(β) die seitliche Luft-Boden-Dämpfung, gegeben durch
| Λ(β) = 1,137 - 0,0229β + 9,72 exp(-0,142β) für 0° ≤β ≤ 50° , | ( 44) |
| Λ(β) = 0 für 50° ≤β ≤ 90° . | ( 45) |
Der Ausdruck für die seitliche Dämpfung Λ(β, ) in Gleichung ( 41) gilt für sämtliche Flugzeuge und ist in Abbildung 15 grafisch dargestellt.
) in Gleichung ( 41) gilt für sämtliche Flugzeuge und ist in Abbildung 15 grafisch dargestellt.
Unter bestimmten Umständen (mit Gelände) kannβ kleiner als null sein. In solchen Fällen wird Λ(β) = 10,857 gesetzt.
Abbildung 15: Änderung der seitlichen Dämpfung Λ(β, ) in Abhängigkeit von Höhenwinkel und Abstand
) in Abhängigkeit von Höhenwinkel und Abstand

21.5 Seitliche Dämpfung und Installationseffekt in endlich langen Segmenten
Die Beschreibung der geometrischen Parameter für die seitliche Dämpfung und den Installationseffekt wird wegen der gemeinsam verwendeten Abbildungen zusammengefasst. Die Gleichungen ( 42) bis (45) beschreiben die seitliche Dämpfung Λ(β, ) des Schalls, der von einem Luftfahrzeug im stationären Flug auf einer unendlichen horizontalen Flugbahn am Immissionsort ankommt. Für nicht horizontal verlaufende Flugbahnsegmente, muss die seitliche Dämpfung ausgehend von einer äquivalenten horizontalen Flugbahn berechnet werden. Die Bestimmung der seitlichen Dämpfung für endliche Segmente erfolgt bei Maximal- und Schallexpositionspegeln auf unterschiedliche Weise.
) des Schalls, der von einem Luftfahrzeug im stationären Flug auf einer unendlichen horizontalen Flugbahn am Immissionsort ankommt. Für nicht horizontal verlaufende Flugbahnsegmente, muss die seitliche Dämpfung ausgehend von einer äquivalenten horizontalen Flugbahn berechnet werden. Die Bestimmung der seitlichen Dämpfung für endliche Segmente erfolgt bei Maximal- und Schallexpositionspegeln auf unterschiedliche Weise.
21.5.1 Seitliche Dämpfung für Maximalpegel
Der SegmentmaximalpegelLpAmax wird anhand von NPD-Daten als Funktion des Abstands d vom Immissionsort zum nächstgelegenen Punkt Ss mits = 1; 2;p im Segment ermittelt.
Für die Abmessungen des Segments sind keine Korrekturen erforderlich. Die seitliche Dämpfung vonLpAmax hängt für Immissionsorte neben dem Segment vom Bodenabstand =
= = OR und vom Höhenwinkelβ = arccos(
= OR und vom Höhenwinkelβ = arccos( /dp) ab. Die Parameter
/dp) ab. Die Parameter undβ sind in diesem Fall für Maximal- und Expositionspegel gleich. Für Segmente hinter oder vor dem Immissionsort hängtLpAmax vom Höhenwinkelβ =βs= arcsin(zs/ds) desselben Punkts und vom Bodenabstand
undβ sind in diesem Fall für Maximal- und Expositionspegel gleich. Für Segmente hinter oder vor dem Immissionsort hängtLpAmax vom Höhenwinkelβ =βs= arcsin(zs/ds) desselben Punkts und vom Bodenabstand =
= * = OCs = √ds2 - zs2 zu diesem Punkt ab. Somit werden nur die Koordinaten dieses Punkts benötigt. In Abbildung 17 sindβ1 undd1 durch das Dreieck OC1S1 in der vertikalen Ebene durch 0 und S1 dargestellt. Für denMaximalpegel ist Λ(β,
* = OCs = √ds2 - zs2 zu diesem Punkt ab. Somit werden nur die Koordinaten dieses Punkts benötigt. In Abbildung 17 sindβ1 undd1 durch das Dreieck OC1S1 in der vertikalen Ebene durch 0 und S1 dargestellt. Für denMaximalpegel ist Λ(β, ) durch die Gleichung ( 41) gegeben.
) durch die Gleichung ( 41) gegeben.
BeiLpAE ist der Prozess jedoch komplizierter.
21.5.2 Seitliche Dämpfung für Expositionspegel
Der Basis-SchallexpositionspegelLpAE(P, d), der für sämtliche Segmente anhand der NPD-Daten bestimmt wird, bezieht sich auf einen unendlichen Flugweg. Der Schallexpositionspegel eines SegmentsLpAE,seg ist daher um den Betrag der Segmentkorrektur ΔF niedriger als der Basispegel. Diese Korrektur, eine Funktion der Geometrie der Dreiecke OS1S2 in Abbildung 10 bis Abbildung 12, legt fest, welcher Anteil der bei 0 empfangenen Schallenergie der unendlichen Gesamtflugbahn vom Segment kommt. Die Segmentkorrektur ΔF ist unabhängig von der seitlichen Dämpfung.
Die seitliche Dämpfung für Schallexpositionspegel ist für die unendliche Flugbahn zu berechnen, d. h. als Funktion ihres seitlichen Versatzes und der Höheh der äquivalenten, horizontalen Flugbahn, nicht der des endlichen Segments. Beim Schallexpositionspegel ist der seitliche Versatz
und der Höheh der äquivalenten, horizontalen Flugbahn, nicht der des endlichen Segments. Beim Schallexpositionspegel ist der seitliche Versatz =
= der senkrechte Abstand zwischen Immissionsort und der auf die Grundebene projizierten Segmentverlängerung. Die Höheh deräquivalenten, horizontalen Flugbahn wird ausgehend von dem Punkt Ss des Segments ermittelt, der am nächsten zum Immissionsort ist, d. h.h =zs/ cos(γ) .h ist dabei die Länge von RSs , der Senkrechten vom Kurs über Grund zum Segment durch den jeweiligen Punkt. Dies entspricht einer Drehung der tatsächlichen verlängerten Flugbahn mit Winkel γ um Punkt R (siehe Abbildung 16 und Abbildung 17). Der Höhenwinkel dieser äquivalenten horizontalen Flugbahn istβ = arctan(h/
der senkrechte Abstand zwischen Immissionsort und der auf die Grundebene projizierten Segmentverlängerung. Die Höheh deräquivalenten, horizontalen Flugbahn wird ausgehend von dem Punkt Ss des Segments ermittelt, der am nächsten zum Immissionsort ist, d. h.h =zs/ cos(γ) .h ist dabei die Länge von RSs , der Senkrechten vom Kurs über Grund zum Segment durch den jeweiligen Punkt. Dies entspricht einer Drehung der tatsächlichen verlängerten Flugbahn mit Winkel γ um Punkt R (siehe Abbildung 16 und Abbildung 17). Der Höhenwinkel dieser äquivalenten horizontalen Flugbahn istβ = arctan(h/ ) .
) .
Abbildung 16 veranschaulicht ein Abflugsegment S1S2 - das Luftfahrzeug steigt im Winkel γ. Der Rest der "realen" Flugbahn ist nicht dargestellt. Das Luftfahrzeug ist gegen den Uhrzeigersinn um die Flugbahn im Winkel ε zur seitlichen Horizontalachse quergeneigt. Der Depressionswinkel Φ der Tragflächenebene, der den Installationseffekt Δ1 beeinflusst (Gleichung ( 40)), liegt in der Ebene senkrecht zur Flugbahn, in derε definiert ist. Somit giltΦ =β1 -ε. Dabei istβ1 = arccos ( /dp) =β = arctan(h /
/dp) =β = arctan(h / ) .Die äquivalente, horizontale Flugbahn wird in der vertikalen Ebene durch S1S2 mit gleichem rechtwinkligen Schrägabstanddp vom Immissionsort definiert. Durch Drehung des Dreiecks ORSp und seiner angebundenen Flugbahn um OR im Winkelγ ergibt sich das Dreieck ORS"p (siehe Abbildung 16). Der Punkt des kleinsten Vorbeiflugabstands des Luftfahrzeugs vom Immissionsort Sp wird durch die Senkrechte OSp der Länge dp definiert (Schrägabstand). Der seitliche Versatz
) .Die äquivalente, horizontale Flugbahn wird in der vertikalen Ebene durch S1S2 mit gleichem rechtwinkligen Schrägabstanddp vom Immissionsort definiert. Durch Drehung des Dreiecks ORSp und seiner angebundenen Flugbahn um OR im Winkelγ ergibt sich das Dreieck ORS"p (siehe Abbildung 16). Der Punkt des kleinsten Vorbeiflugabstands des Luftfahrzeugs vom Immissionsort Sp wird durch die Senkrechte OSp der Länge dp definiert (Schrägabstand). Der seitliche Versatz ist gegeben durch die Strecke OR. Das Dreieck OS1S2 entspricht Abbildung 11, der Geometrie für die Berechnung der Segmentkorrektur ΔF.
ist gegeben durch die Strecke OR. Das Dreieck OS1S2 entspricht Abbildung 11, der Geometrie für die Berechnung der Segmentkorrektur ΔF.
Abbildung 16: Immissionsort neben dem Segment

Abbildung 17: Immissionsort hinter dem Segment
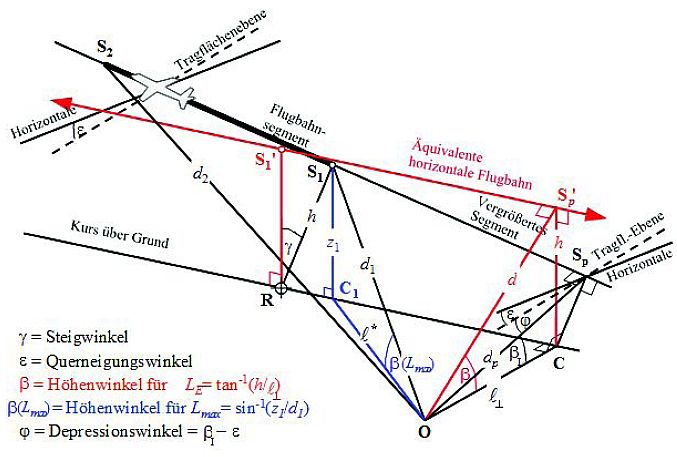
Abbildung 17 veranschaulicht die Situation eines Abflugs, in der der Immissionsort Ohinter dem Segment liegt. Dieses Segment liegt gegenüber dem neben dem Immissionsort befindlichen Segment in größerer Entfernung zum Immissionsort; eine Senkrechte kann nur zum Punkt Sp auf der verlängerten Flugbahn gezogen werden. Das Dreieck OS1S2 entspricht Abbildung 10, in der die Segmentkorrektur ΔF definiert wird. Bei der Berechnung der seitlichen Dämpfung fürSchallexpositionspegel bei Segmenten vor oder hinter dem Immissionsort bleibt =
=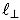 der seitliche Versatz von der Segmentverlängerung (OC) und β = arctan(h/
der seitliche Versatz von der Segmentverlängerung (OC) und β = arctan(h/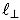 ) . Die Höhe deräquivalenten, horizontalen Flugbahn ergibt sich aus der Höhe des Segmentpunkts, der am nächsten zum Immissionsort ist, d. h. aus S1 mit h = z1/ cos(γ) (der Länge von RS1, der Senkrechten vom Kurs über Grund zum Segment). Der kleinste Abstand der äquivalenten, horizontalen Flugbahn zum Immissionsort O liegt beiS"p , Schrägabstandd, so dass das auf diese Weise in der vertikalen Ebene gebildete Dreieck OCS"p den Höhenwinkelβ = arctan(h/
) . Die Höhe deräquivalenten, horizontalen Flugbahn ergibt sich aus der Höhe des Segmentpunkts, der am nächsten zum Immissionsort ist, d. h. aus S1 mit h = z1/ cos(γ) (der Länge von RS1, der Senkrechten vom Kurs über Grund zum Segment). Der kleinste Abstand der äquivalenten, horizontalen Flugbahn zum Immissionsort O liegt beiS"p , Schrägabstandd, so dass das auf diese Weise in der vertikalen Ebene gebildete Dreieck OCS"p den Höhenwinkelβ = arctan(h/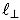 ) definiert. Liegt der Immissionsort beim Abflug vor dem Segment, ergibt sich die Höhe h ausS2. Liegt der Immissionsort beim Anflug vor dem Segment, ergibt sich die Höhe h ausS1. Liegt der Immissionsort beim Anflug hinter dem Segment, ergibt sich die Höhe h ausS2. (Der NPD-Abstandsparameter für die Situation in Abbildung 17 ist für Maximalpegel der kürzeste Abstand zum Segment, d. h.d = d1 und für Expositionspegel der kürzeste Abstanddp zwischen O und Sp auf der verlängerten Flugbahn, d. h. der anhand der NPD-Tabelle interpolierte Wert istLpAE∞(P1,dp) ).
) definiert. Liegt der Immissionsort beim Abflug vor dem Segment, ergibt sich die Höhe h ausS2. Liegt der Immissionsort beim Anflug vor dem Segment, ergibt sich die Höhe h ausS1. Liegt der Immissionsort beim Anflug hinter dem Segment, ergibt sich die Höhe h ausS2. (Der NPD-Abstandsparameter für die Situation in Abbildung 17 ist für Maximalpegel der kürzeste Abstand zum Segment, d. h.d = d1 und für Expositionspegel der kürzeste Abstanddp zwischen O und Sp auf der verlängerten Flugbahn, d. h. der anhand der NPD-Tabelle interpolierte Wert istLpAE∞(P1,dp) ).
ANMERKUNG: Es wird darauf hingewiesen, dass die Geometrie der Basisquelle (definiert durch d1 , d2 undΦ) unberührt bleibt. Der sich vom Segment zum Immissionsort bewegende Schall ist mit dem Schall identisch, der auftreten würde, wenn der gesamte Flug entlang dem unendlich verlängerten geneigten Segment mit der konstanten GeschwindigkeitV und der konstanten LeistungP1 erfolgen würde. Andererseits steht die seitliche Dämpfung des am Immissionsort vom Segment empfangenen Schalls nicht in Beziehung zuβ1 , dem Höhenwinkel der verlängerten Flugbahn, sondern zuβ, dem Höhenwinkel der äquivalenten Bahn.
Befindet sich der Immissionsort beim Abflug hinter den Bodensegmenten und beim Anflug vor den Bodensegmenten, wird der Wert vonβ der gleiche wie beim Maximalpegelmaß, d. h. für Positionen hinter den Startrollstreckensegmenten bzw. vor den Landerollsegmenten gilt:
β =β1 = arcsin (z1 /d1) und = = * = OC1 = √d21 -z21 . * = OC1 = √d21 -z21 . |
( 46) |
21.5.3 Installationseffekt
Die laterale Richtcharakteristik (Installationseffekt) ist zweidimensional, daher wird der DepressionswinkelΦ immer in der Ebene, die senkrecht zur Flugbahn steht, ermittelt. Somit wird der Depressionswinkel am Punkt des kleinsten Vorbeiflugabstands bestimmt, d. h. =Φ - β1 -ε , wobeiβ1 = arccos(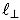 /dp) und
/dp) und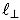 der seitliche Versatz, der senkrecht auf dem Kurs über Grund steht, ist.β1 ist in Abbildung 17 durch den Winkel SpOC und in Abbildung 16 durch den Winkel SOR (β) dargestellt.
der seitliche Versatz, der senkrecht auf dem Kurs über Grund steht, ist.β1 ist in Abbildung 17 durch den Winkel SpOC und in Abbildung 16 durch den Winkel SOR (β) dargestellt.
21.6 Segmentkorrektur ΔF (nur für SchallexpositionspegelLpAE)
Der korrigierte Basis-Schallexpositionspegel bezieht sich auf ein Luftfahrzeug im stationären, horizontalen und unendlich langen Geradeausflug. Durch Anwendung der negativen Segmentkorrektur ΔF = 10 lg(F), wobeiF derEnergieanteil ist, erhält man die Schallenergie, die das Luftfahrzeug beim Passieren eines endlich langen Segments abstrahlen würde.
Der Term für den Energieanteil berücksichtigt die ausgeprägte longitudinale Richtcharakteristik des Fluglärms und ist abhängig vom Winkel zwischen Flugrichtung und Luftfahrzeug-Immissionsort-Vektor. Der weiter unten angegebene Ausdruck für ΔF basiert auf einem 90-Grad-Dipol-Modell der vierten Potenz für die Schallabstrahlung. Dabei wird angenommen, dass die laterale Richtcharakteristik und seitliche Dämpfung keinen Einfluss haben. Die Herleitung dieser Segmentkorrektur wird in Anhang E beschrieben.
Der EnergieanteilF ist eine Funktion des in Abbildung 10 bis Abbildung 12 definierten "Sichtdreiecks". Für die Segmentkorrektur ΔF ergibt sich somit Folgendes:
 |
( 47) |
Dabei gilt:
| α1 = - (q / dλ) , | ( 48) |
| α2 = (q -λ / dλ) , | ( 49) |
| dλ = 10[LpAmax∞(P, dp) - LpAmax(P, dp)] / 10 , | ( 50) |
| do = (2 / π) · Vref · to . | ( 51) |
dλ wird als "skalierter Abstand" bezeichnet (siehe Anhang E);Vref = 160 kt . Zu beachten ist, dassLpAmax(P, dp) der anhand der NPD-Daten ermittelte Maximalpegel für den senkrechten Abstanddp und nicht derLpAmax des Segments ist.
Für ΔF wird eine Untergrenze von -150 dB gesetzt.
In dem besonderen Fall, dass sich die Immissionsorte hinter jedem Startrollstreckensegment oder jedem Landerollstreckensegment befinden, wird eine reduzierte Form des in Gleichung ( 47) ausgedrückten Lärmanteils verwendet, die dem spezifischen Fall vonq = 0 entspricht. Die Berechnung erfolgt unter Verwendung von
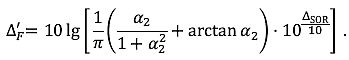 |
( 52) |
Dabei gilt α2 =λ/dλ · ΔsoR ist die durch die Gleichungen ( 57) und ( 58) definierte Richtwirkungsfunktion am Start-of-Roll-Punkt.
Die Gründe für die Verwendung dieser besonderen Form des Lärmanteils werden im nachfolgenden Abschnitt 21.7 im Rahmen der Anwendungsmethode für die Richtcharakteristik am Start-of-Roll-Punkt näher erläutert.
21.7 Spezifische Behandlung der Rollsegmente, einschließlich Richtwirkungsfunktion am Start-of-Roll-Punkt ΔsoR
Bei den Startroll- und Landerollsegmenten erfolgt eine spezifische Behandlung, die im Folgenden erläutert wird.
21.7.1 Richtwirkungsfunktion am Start-of-Roll-Punkt ΔsoR
Das Geräusch von Strahlflugzeugen weist eine für Strahltriebwerkslärm typische keulenförmige Abstrahlcharakteristik im hinteren Bogen auf. Diese Charakteristik ist umso ausgeprägter, je höher die Strahlgeschwindigkeit ist und je niedriger die Fluggeschwindigkeit liegt. Von besonderer Bedeutung ist dies für Immissionsorte hinter dem Start-of-Roll-Punkt, wo beide Bedingungen erfüllt sind. Dieser Effekt wird durch eine Richtwirkungsfunktion ΔsoR berücksichtigt.
Abbildung 18 zeigt die entsprechenden geometrischen Verhältnisse. Der Azimutwinkelψ zwischen der Längsachse des Luftfahrzeugs und dem Vektor zum Immissionsort ist definiert durch
| ψ = arccos (q / dSOR) | ( 53) |
Der relative Abstandq ist negativ (siehe Abbildung 10), so dass sich ip zwischen 90° und 180° bewegt.
Abbildung 18: Geometrie Luftfahrzeug - Immissionsort am Boden zur Abschätzung der Richtwirkungskorrektur
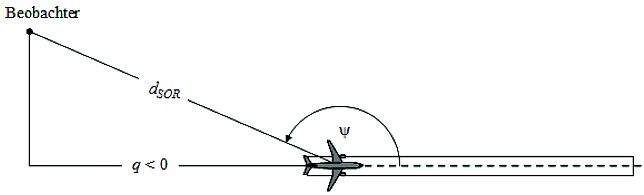
Die Funktion ΔsoR stellt die Differenz des von der Startrollstrecke ausgehenden Gesamtlärms hinter dem Start-of-Roll-Punkt, gegenüber dem Gesamtlärm der Startrollstrecke seitlich des Start-of-Roll-Punkts im gleichen Abstand, dar:
| LTGR(dSOR,ψ) =LTGR(dSOR, 90°) + ΔSOR (dSOR,ψ) | ( 54) |
Dabei istLTGR (dSOR, 90°) der von allen Startrollsegmenten im PunktabstanddSOR seitlich des Start-of-Roll-Punkts erzeugte Startrollstrecken-Gesamtlärmpegel.
Bei AbständendSOR von weniger als einem NormalisierungsabstanddSOR,O = 762 m (2.500 ft) ist die Richtwirkungsfunktion am Start-of-Roll-Punkt gegeben durch
| Δ0SOR = 51,47 - 1,553ψ + 0,015147ψ2 - 0,000047173ψ3
wenn 90° ≤ψ < 148,4° , |
( 55) |
| Δ0SOR = 339,18 - 2,5802ψ - 0,0045545ψ2 + 0,000044193ψ3
wenn 148,4° ≤ψ ≤ 180°. |
( 56) |
Ist der Abstand dSOR größer als der NormalisierungsabstanddSOR,O , wird die Richtwirkungskorrektur mit einem Korrekturfaktor multipliziert, um zu berücksichtigen, dass die Richtwirkung bei größeren Abständen zum Luftfahrzeug weniger ausgeprägt ist; d. h.:
| ΔSOR = Δ0SOR wenn dSOR ≤ dSOR,0 , | ( 57) |
| ΔSOR = Δ0SOR (dSOR,0 / dSOR) = wenn dSOR > dSOR,0 . | ( 58) |
ANMERKUNG: Die Gleichungen ( 53) bis (58) gelten nicht für Propellerflugzeuge.
21.7.2 Behandlung von Immissionsorten, die sich hinter jedem Startrollstrecken- und Landerollsegment befinden
Die Funktion ΔSOR erfasst vor allem die ausgeprägte Richtwirkung des Anfangsabschnitts der Startrollstrecke an Orten hinter dem Start-of-Roll-Punkt. Sie ist jedoch auf Positionen hinterjedem einzelnen Startrollstrecken- wie auch Landerollsegment anzuwenden also nicht nur hinter dem Start-of-Roll-Punkt.
Die Parameterds undψ werden bezogen auf den Anfang jedes einzelnen Rollsegments berechnet.
Die Berechnung des SegmentwertsLseg für einen Ort hinter einem bestimmten Startroll stecken- oder Landerollsegment erfolgt zur Einhaltung der Formanforderungen der Funktion ΔSOR: Er wird im Wesentlichen für den seitlich des Startpunkts des Segments im gleichen Abstandds wie der eigentliche Punkt gelegenen Bezugspunkt berechnet und mit ΔSOR weiter angepasst, so dass sich der Segmentwert am eigentlichen Punkt ergibt.
Das bedeutet, dass die verschiedenen Korrekturterme in den nachstehenden Gleichungen die geometrischen Parameter verwenden müssen, die diesem seitlich des Startpunkts gelegenen Bezugspunkt entsprechen:
LpAmax,seg =LpAmax(P, d = ds) + ΔI(Φ) - Λ(β, = ds) + ΔSOR = ds) + ΔSOR |
( 59) |
LpAE,seg =LpAE,∞(P, d = ds) + Δv + ΔI(Φ) - Λ(β, = ds) + Δ"F ΔSOR . = ds) + Δ"F ΔSOR . |
( 60) |
Dabei ist Δ"F die in Gleichung ( 52) ausgedrückte reduzierte Form des Lärmanteils für den Fallq = 0. Es sei daran erinnert, dassdλ unter Verwendung vonds (und nicht vonds) zu berechnen ist:
| dλ = d0 · 10[LpAE,∞(P, ds)-LpAmax(P, ds)] / 10 | ( 61) |
22 Maximal- und Schallexpositionspegel der Flugbewegung eines Luftfahrzeugs der Allgemeinen Luftfahrt
Die in Abschnitt 21 beschriebene Methode ist auf Propellerflugzeuge der Allgemeinen Luftfahrt anwendbar, wenn sie hinsichtlich der Triebwerksanbringungseffekte als Propellerflugzeuge behandelt werden.
Luftfahrzeuge der Allgemeinen Luftfahrt werden mit den entsprechenden Luftfahrzeuggruppen beschrieben, die in Anhang A definiert und in der BUF-D aufgeführt sind.
23 Methode zur Berechnung von Hubschrauberlärm
Zur Berechnung von Hubschrauberlärm wird die gleiche Berechnungsmethode verwendet wie für Starrflügelflugzeuge. Dabei werden Hubschrauber wie Propellerflugzeuge behandelt und der mit Strahlflugzeugen verbundene Triebwerksanbringungseffekt nicht berücksichtigt. Datensätze für Hubschrauber sind in der BUF-D aufgeführt.
24 Lärm im Zusammenhang mit Triebwerksprobeläufen, Rollverkehr und Hilfstriebwerken
Soll Lärm im Zusammenhang mit Triebwerksprobeläufen und Hilfstriebwerken (APUs) modelliert werden, erfolgt diese Modellierung gemäß dem in der "Berechnungsmethode für den Umgebungslärm von bodennahen Quellen (Straßen, Schienenwege, Industrie und Gewerbe) (BUB)" beschriebenen Verfahren für "Industrie- und Gewerbelärm".
Aus zusätzlichen Sicherheits- und Lärmschutzgründen können auf Flugplätzen - vor allem Flugplätze mit Wartungseinrichtungen, in denen häufig Triebwerksprüfungen stattfinden - Lärmschutzeinrichtungen für Triebwerksprobeläufe (z.B. offene oder geschlossene Lärmschutzhallen) vorhanden sein. Diese sollen als Quelle von Industrielärm betrachtet und durch die Anwendung eines geeigneten Schallausbreitungsmodells berücksichtigt werden.
25 Berechnung kumulativer Pegel
In den Abschnitten 16 bis 21 wird die Berechnung des Schallexpositionspegels einer einzelnen Flugbewegung an einem einzelnen Immissionsort beschrieben. Die Berechnung der Gesamtschallexposition an diesem Ort erfolgt durch Akkumulierung der Schallexpositionspegel aller Flugbewegungen, d. h. aller ankommenden und abgehenden Flüge sowie gegebenenfalls Triebwerksprobeläufe und Hilfstriebwerken, die den kumulativen Pegel beeinflussen.
26 Äquivalenter Dauerschallpegel
Der äquivalente DauerschallpegelLpeq,W für einen bestimmten Zeitabschnitt W (Tag, Abend oder Nacht), berücksichtigt den Lärm, der von sämtlichen Flugbewegungen - und gegebenenfalls Triebwerksprobeläufen und Hilfstriebwerken - ausgeht und wird mit der folgenden Gleichung ausgedrückt:
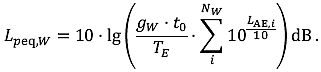 |
( 62) |
Die Addition erfolgt über sämtliche LärmereignisseNW für eine ErhebungszeitTE = 365 d während des ZeitintervallstW (je nach Zeitabschnitt 12 h, 8 h oder 4 h).
Hierbei gilt:
| to | Bezugszeitto = 1 s ; |
| LpAE,i | Schallexpositionspegel des i-ten Lärmereignisses; |
| gW | tageszeitabhängiger Gewichtungsfaktor, der berücksichtigt, dass je nach ZeitabschnittW (Tag, Abend und Nacht) nur über dessen prozentualen Anteil am gesamten Tag in der Erhebungszeit summiert wird. Daher gilt:gW = 2 (Tag); 6 (Abend); 3 (Nacht). |
27 Kumulativer Lärmpegel LDEN
Der kumulative LärmpegelLDEN wird durch Addition der Beiträge aller verschiedenen Muster oder Kategorien von Luftfahrzeugen auf den Flugstrecken in der Flugplatzumgebung bestimmt. Zur Beschreibung dieses Additionsprozesses werden die folgenden tiefgestellten Indizes eingeführt:
| i | Index für Luftfahrzeugmuster oder -kategorie, |
| j | Index für Flugstrecke oder Unterstrecke, |
| k | Index für Flugstreckensegment. |
Der Additionsprozess lässt sich durch Einführung einer "gewichteten Zahl der Flüge" vereinfachen:
| Mij = (Nij, Day +Nij, Evening · 105/10 +Nij, Night · 1010/10) . | ( 63) |
Die WerteNij stellen die Zahl der Flüge des Luftfahrzeugmusters oder der Luftfahrzeugkategoriei auf der Strecke (oder Unterstrecke)j in den Zeitabschnitten Tag, Abend bzw. Nacht dar 15. Die Faktoren 105/10 bzw. 1010/10 stellen Zuschläge nach § 2 der Verordnung über die Lärmkartierung ( 34. BImSchV) dar, mit denen Flüge am Abend bzw. in der Nacht bewertet werden.
Anhand der Gleichung ( 64) ist der kumulative LärmpegelLDEN an einem bestimmten Immissionsort
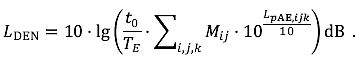 |
( 64) |
TE ist die Erhebungszeit von einem Jahr.LpAE,ijk ist der Schallexpositionspegelbeitrag des Segmentsk von Strecke oder Unterstreckej für den Flug eines Luftfahrzeugs der Kategoriei. Die Berechnung vonLpAE,ijk wird in den Abschnitten 16 bis 21 beschrieben.
28 Standardgitterberechnung
28.1 Rechengitter
Die Berechnung der ImmissionskenngrößenLDEN undLNight erfolgt an den Punkten eines rechtwinkligen Gitters. Die Maschenweite des Gitters beträgt generell 50 m. Die Achsen des Rechengitters sind parallel zu den Rechts- und Hochachsen des verwendeten Koordinatensystems. Das Gitter ist so zu definieren, dass die Tausenderwerte des Koordinatensystems mit Gitterpunkten zusammenfallen. Die Berechnung erfolgt in der Höhez = 0 m über Grund.
28.2 Berechnung der Kurvenpunkte
Ausgehend von den für die Punkte des Rechengitters bestimmten Werten der Immissionskenngrößen werden Punkte mitLDEN = const. undLNight = const. durch lineare Interpolation zwischen den horizontal und vertikal benachbarten Gitterpunkten ermittelt. Diese Punkte werden als Kurvenpunkte bezeichnet. Die Kurvenpunkte werden ohne Glättungsverfahren zu einer Isolinie verbunden. Die Isolinie schließt entweder eine Tag-Abend-Nacht-Zone oder eine Nacht-Zone ein.
ANMERKUNG: Wenn Lärmkonturen durch Interpolation zwischen Indexwerten an rechteckig angeordneten Gitterpunkten ermittelt werden, hängt ihre Genauigkeit von der Wahl der Gitterweite (Maschenweite) ΔG ab, vor allem innerhalb von Zellen, in denen ein großes Gefälle bei der räumlichen Verteilung des Index zu einer engen Krümmung der Konturen führt. Durch eine engere Gitterweite lassen sich Interpolationsfehler reduzieren, doch erhöht sich damit die Zahl der Gitterpunkte, was die Berechnungszeit verlängert. Für eine Optimierung der Gitterweite müssen Modellierungsgenauigkeit und Laufzeit gegeneinander abgewogen werden.
| Anhang |
A Datenanforderungen
A.1 Anleitung zur Datenerfassung an Flugplätzen (AzDF)
A.1.1 Anwendungsbereich
Das "Datenerfassungssystem (DES)" dient der Beschaffung der Eingabedaten zur Ausarbeitung der Lärmkarten an Großflughäfen und in Ballungsräumen an sonstigen Flugplätzen für den zivilen Luftverkehr nach § 47c des Bundes-Immissionsschutzgesetzes sowie der Verordnung über die Lärmkartierung ( 34. BImSchV). Es enthält detaillierte Angaben über den Flugbetrieb des Flugplatzes und den Verlauf der Flugstrecken in der Flugplatzumgebung. Die Daten des Datenerfassungssystems werden anhand der vorliegenden "Anleitung zur Datenerfassung an Flugplätzen (AzDF)" ermittelt. Auf der Grundlage der mit dem Datenerfassungssystem erhobenen Daten über Art und Umfang des Flugbetriebes erfolgt die Fluglärmberechnung.
A.1.2 Erforderliche Angaben
Erforderliche Angaben zur Ermittlung der Lärmkarten beziehen sich auf das "Ist-Jahr"; das Ist-Jahr ist das vorausgegangene Kalenderjahr. Im Einzelnen sollten insbesondere folgende Angaben genutzt werden:
A.1.3 Luftfahrzeugbezeichnungen
Für alle Luftfahrzeuge werden Luftfahrzeuggruppen bzw. -klassen verwendet. Die Luftfahrzeugklasse spezifiziert die Luftfahrzeuggruppe hinsichtlich des Starts oder der Landung und erhält eine entsprechende Erweiterung (Luftfahrzeuggruppe X, Luftfahrzeugklasse X-S bzw. X-L). Dabei werden zwei Arten unterschieden, und zwar
Die zu benutzenden Luftfahrzeuggruppen der ICAO sind in Tabelle 12 der BUF-D aufgeführt und im ICAO Dokument 8643 "Aircraft type Designators" erläutert. Die Luftfahrzeuggruppen in Tabelle A.1 sind in Anlehnung an die Anleitung zur Berechnung von Lärmschutzbereichen (AzB) nach dem Gesetz zum Schutz gegen Fluglärm definiert. Grundsätzlich sind für die Angabe der Flugbewegungen die Luftfahrzeuggruppen aus Tabelle 12 der BUF-D zu verwenden. Sofern ein Luftfahrzeug keine ICAO-ATD besitzt oder seine ICAO-ATD nicht in Tabelle 12 der BUF-D aufgeführt ist, wird für dieses Luftfahrzeug die entsprechende Luftfahrzeuggruppe gemäß Tabelle A.1 verwendet.
Tabelle A.1: Definition der Luftfahrzeuggruppen für Luftfahrzeuge ohne ICAO-ATD
| Luftfahrzeuggruppen | Definition |
| P 1.0 | Ultraleichtflugzeuge |
| P 1.1 | Motorsegler |
| P 1.2 | Propellerflugzeuge mit einer Höchststartmasse (Maximum Take-Off Mass, MTOM) bis 2 t oder Motorsegler beim Segelflugzeugschlepp |
| P 1.3 | Propellerflugzeuge mit einer Höchststartmasse (MTOM) bis 2 t |
| P 1.4 | Propellerflugzeuge mit einer Höchststartmasse (MTOM) von 2 t bis 5,7 t |
| P 2.1 | Propellerflugzeuge mit einer Höchststartmasse (MTOM) über 5,7 t, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt16, Band I, Kapitel 3, 4, 10 oder 14 entsprechen. |
| P 2.2 | Propellerflugzeuge mit einer Höchststartmasse (MTOM) über 5,7 t, die nicht der Luftfahrzeuggruppe P 2.1 zugeordnet werden können. |
| S 1.0 | Strahlflugzeuge mit einer Höchststartmasse (MTOM) bis 34 t, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 2 entsprechen. |
| S 1.1 | Strahlflugzeuge mit einer Höchststartmasse (MTOM) über 34 t bis 100 t, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 2 entsprechen (ohne die Luftfahrzeugmuster Boeing 737 und Boeing 727). |
| S 1.2 | Luftfahrzeuge des Luftfahrzeugmusters Boeing 737, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 2 entsprechen. |
| S 1.3 | Luftfahrzeuge des Luftfahrzeugmusters Boeing 727, die den Anforderungen des Anhangs 16 zum Abkommen über die internationale Zivilluftfahrt, Band I, Kapitel 2 entsprechen. |
| S 2 | Strahlflugzeuge mit einer Höchststartmasse (MTOM) bis 100 t, die nicht den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I entsprechen. |
| S 3.1 | Strahlflugzeuge mit zwei oder drei Triebwerken und einer Höchststartmasse (MTOM) über 100 t, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 2 oder 3 entsprechen und vor 1982 gebaut wurden. |
| S 3.2 | Strahlflugzeuge mit vier Triebwerken und einer Höchststartmasse (MTOM) über 100 t, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 2 oder 3 entsprechen und vor 1982 gebaut wurden. |
| S 4 | Strahlflugzeuge mit einer Höchststartmasse (MTOM) über 100 t, die nicht den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I entsprechen. |
| S 5.1 | Strahlflugzeuge mit einer Höchststartmasse (MTOM) bis 50 t, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 3, 4 oder 14 entsprechen. |
| S 5.2 | Strahlflugzeuge mit einer Höchststartmasse (MTOM) über 50 t bis 120 t und einem Triebwerks-Nebenstromverhältnis größer als 3, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 3, 4 oder 14 entsprechen. |
| S 5.3 | Strahlflugzeuge mit einer Höchststartmasse (MTOM) über 50 t bis 120 t und einem Triebwerks-Nebenstromverhältnis bis 3, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 3, 4 oder Kapitel 14 entsprechen. |
| S 6.1 | Strahlflugzeuge mit zwei Triebwerken und einer Höchststartmasse (MTOM) über 120 t, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 3, 4 oder 14 entsprechen. |
| S 6.2 | Strahlflugzeuge mit drei oder vier Triebwerken und einer Höchststartmasse (MTOM) über 120 t bis 300 t, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 3, 4 oder 14 entsprechen. |
| S 7 | Strahlflugzeuge mit drei oder vier Triebwerken und einer Höchststartmasse (MTOM) über 300 t bis 500 t, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 3, 4 oder 14 entsprechen. |
| S 8 | Strahlflugzeuge mit mindestens vier Triebwerken und einer Höchststartmasse (MTOM) über 500 t, die den Anforderungen des Anhangs 16 zum Abkommen über die Internationale Zivilluftfahrt, Band I, Kapitel 3, 4 oder 14 entsprechen. |
| P-MIL 1 | Militärische Propellerflugzeuge mit einer Höchststartmasse (MTOM) bis 5,7 t |
| P-MIL 2 | Militärische Propellerflugzeuge mit einer Höchststartmasse (MTOM) über 5,7 t |
| S-MIL 1 | E-3 AWACS (Airborne Warning and Control System), E-8 Joint Stars, C-135F, KC-135, RC-135, C-5A/B Galaxy |
| S-MIL 2 | F-4 Phantom, F-22 Raptor |
| S-MIL 3 | Tornado |
| S-MIL 4 | F-15, F-16 |
| S-MIL 5 | A-10/0A-10 Thunderbolt II |
| S-MIL 6 | Eurofighter |
| H 1.0 | Hubschrauber mit einer Höchststartmasse (MTOM) bis 1,0 t |
| H 1.1 | Hubschrauber mit einer Höchststartmasse (MTOM) über 1,0 t bis 3,0 t |
| H 1.2 | Hubschrauber mit einer Höchststartmasse (MTOM) über 3,0 t bis 5,0 t |
| H 2.1 | Hubschrauber mit einer Höchststartmasse (MTOM) über 5,0 t bis 10,0 t |
| H 2.2 | Hubschrauber mit einer Höchststartmasse (MTOM) über 10,0 t |
A.1.4 Flugstreckenbeschreibung
A.1.4.1 Erfassungsbereich
In das Datenerfassungssystem sind alle im Ist-Jahr benutzten Flugstrecken einzutragen, und zwar bis zu einem Radius von mindestens 25.000 m um den Flugplatzbezugspunkt. Bei Sichtflugstrecken kann davon abgewichen werden, wenn sich bis zu dieser Entfernung keine verlässliche Streckenbeschreibung erstellen lässt. In diesem Fall sind die Sichtflugstrecken bis zu einem Radius von mindestens 15.000 m um den Flugplatzbezugspunkt zu beschreiben.
A.1.4.2 Flugstreckenlängen
Längenangaben werden im Datenerfassungssystem in der Einheit "Meter (m)" angegeben.
A.1.4.3 Flugstreckenbezeichnungen
Die Bezeichnungen der Instrumentenflugstrecken können Instrumentenflugkarten entnommen werden. Für Sichtflugstrecken liegen häufig keine Bezeichnungen vor. In diesem Fall ist im Datenerfassungssystem folgender Aufbau zu verwenden:
Entsprechend ist bei Platzrunden zu verfahren.
A.1.4.4 Koordinatentransformationen
Flugstrecken können in einem Koordinatensystem angegeben werden, dem entweder das Ellipsoid und Datum WGS84 oder das Ellipsoid GRS80 und das Datum ETRS89 zugrunde liegt. Die Flugstrecken liegen üblicherweise in einem geographischen Koordinatensystem (WGS84-System) vor, während die Fluglärmkonturen in einem geodätischen Koordinatensystem (UTM (Universal Transverse Mercator)-System) dargestellt werden. Es muss daher in der Regel eine Koordinatentransformation der Flugkurse von rechtweisend Nord (True North, TN) auf Gitter-Nord UTM (GN UTM) vorgenommen werden. Dabei müssen zunächst die Richtungen der Start- und Landebahn von TN auf GN UTM umgerechnet werden. Als Ergebnis erhält man die Meridiankonvergenz, d. h. den Winkel zwischen TN und GN.
Für die weiteren Schritte ist zwischen Instrumenten- und Sichtflugstrecken zu unterscheiden. Instrumentenflugstrecken sind durch Funknavigationsanlagen oder -verfahren festgelegte Flugstrecken, auf denen die Luftfahrzeuge nach Instrumentenflugregeln fliegen. Diese Flugstrecken sind in den einschlägigen Publikationen (z.B."Luftfahrthandbuch Deutschland") veröffentlicht. Die in den Instrumentenflugkarten angegebenen Flugkurse werden bezogen auf rechtweisend Nord aufbereitet. Diese Kurse sind dann noch um die Meridiankonvergenz zu korrigieren. Es muss daher bereits bei der Beschreibung der Flugstrecken eine Koordinatentransformation vorgenommen werden.
Hinsichtlich der Sichtflugstrecken gilt Folgendes: Sichtflüge werden nach Sichtflugregeln durchgeführt und basieren auf dem Prinzip "sehen und gesehen werden"; d. h. der Luftfahrzeugführer kann sich im gesamten Luftraum frei bewegen, soweit dies nicht durch andere Bestimmungen eingeschränkt ist. Der Luftfahrzeugführer führt seinen Flug nach terrestrischer Navigation durch. Dabei erfolgt der Flug entlang markanter Punkte oder Linien auf der Erde (z.B. Eisenbahnstrecken). Aufgrund der örtlichen Gegebenheiten werden daher von den nach Sichtflugregeln fliegenden Luftfahrzeugführern bestimmte Flugwege verstärkt benutzt. Diese Sichtflugstrecken werden in eine topographische Karte eingetragen und im Datenerfassungssystem beschrieben.
A.1.4.5 Abweichende Flugstrecken (Radarvectoring, Direct Routing)
In der flugbetrieblichen Praxis kommt es vor, dass der Luftfahrzeugführer von der Flugsicherung bestimmte Kursanweisungen über Sprechfunk erhält ("Radarvectoring"). Diese Flugwege weichen somit von den in den Luftfahrtkarten veröffentlichten Flugstrecken ab. Darüber hinaus besteht die Möglichkeit, dass der Flugsicherungslotse dem Luftfahrzeugführer die Genehmigung erteilt, auf dem kürzesten Weg zum nächsten Navigationspunkt zu fliegen ("Direct Routing"). Die sich aufgrund dieser Flugsicherungsverfahren ergebenden Flugstrecken sind in das Datenerfassungssystem aufzunehmen, sofern sie im Ist-Jahr häufig genutzt wurden.
A.1.4.6 Korridorbreiten
Die Flugstrecken werden im Datenerfassungssystem mit Korridorbreiten beschrieben, die die Abweichung der Luftfahrzeuge von der Flugstrecke angeben. Die Korridorbreiten sollten unter Verwendung eines Flugwegaufzeichnungssystems, z.B. FANOMOS, für die einzelnen Flugstrecken festgelegt werden, sofern dieses System am jeweiligen Flugplatz zur Verfügung steht. Andernfalls sind die Korridorbreiten aufgrund der örtlichen flugbetrieblichen Praxis zu schätzen. Sofern eine derartige Schätzung nicht möglich ist, ist eine Korridoraufweitung vom 0,2-fachen der längs der Flugstrecke zurückgelegten Bogenlänge bis auf einen Wert von 3.000 m anzusetzen.
A.1.5 Erläuterungen zum Ausfüllen der Datenblätter für Flugplätze
Zu Abschnitt 1 "Allgemeines"
Nummer 1.2:
Das "Ist-Jahr" ist das vorausgegangene Kalenderjahr.
Zu Abschnitt 2 "Flugplatzdaten"
Nummern 2.1 bis 2.3:
Die Daten sind dem Luftfahrthandbuch Deutschland zu entnehmen, sofern keine genaueren Angaben vorliegen.
Nummer 2.4:
Die Dateneinträge für die Zeilen 1, 3 und 4 sind dem Luftfahrthandbuch Deutschland zu entnehmen, sofern keine genaueren Angaben vorliegen.
In Zeile 2 ist anzugeben, ob die Start- und Landebahn bereits vorhanden oder für welches Jahr ihre Inbetriebnahme geplant ist.
In Zeile 3 ist die rechtweisende Richtung der Start- und Landebahn in Dezimalgrad auf 1/1.000 Grad genau anzugeben. Die Angaben sind sowohl bezogen auf geographisch Nord (WGS84) als auch bezogen auf Gitter-Nord (UTM-Abbildung, entsprechend der Lage des Flugplatzes in Zone 32 oder 33 (Mittelmeridian 9° oder 15°), Ellipsoid GRS80, Datum ETRS89) zu machen. Die Angaben im UTM-System sind zentimetergenau im Datenerfassungssystem auszuweisen.
In Zeile 7 ist für beide Startrichtungen die Entfernung des Startpunktes vom Bahnbezugspunkt anzugeben. Dabei gehört der Wert, der in Zeile 7 vor dem Schrägstrich anzugeben ist, zu der Richtung, die in Zeile 1 vor dem Schrägstrich bezeichnet ist. Entsprechendes gilt für die Zeilen 8 und 9.
Liegt der Startpunkt - vom Bahnanfang in Startrichtung gesehen - hinter dem Bahnbezugspunkt, so hat der Wert ein negatives Vorzeichen.
Der zu einer Betriebsrichtung gehörende Startpunkt und die zu dieser Betriebsrichtung gehörende Landeschwelle befinden sich jeweils am gleichen Ende der Start- und Landebahn. Sofern eine Bahn über mehrere Startpunkte verfügt (Intersection-Starts), so ist für jeden Startpunkt eine separate Bahn zu definieren.
Für die Bestimmung der Flugplatz- und Bahnbezugspunkte sind die geographischen Koordinaten auf 1/1.000 Winkelsekunde genau anzugeben. Die Angaben im UTM-System sind zentimetergenau im Datenerfassungssystem auszuweisen.
Zu Abschnitt 3 "Flugbewegungsangaben"
Die Daten über den Flugbetrieb umfassen alle Flugbewegungen, die vom Flugplatz ausgehen (Starts) und die zum Flugplatz führen (Landungen) sowie alle Platzrundenflüge am Flugplatz.
Eine Flugbewegung ist ein Start oder eine Landung. Es sind die Flugbewegungen von allen Luftfahrzeugen im Ist-Jahr zu erfassen. Hierfür sind grundsätzlich die in Tabelle 12 der BUF-D aufgeführten Luftfahrzeuggruppen der ICAO zu verwenden. Ist ein Luftfahrzeug nicht in Tabelle 12 der BUF-D enthalten, weil es keine ICAO-ATD hat oder seine ICAO-ATD nicht in Tabelle 12 der BUF-D aufgeführt ist, wird für dieses eine entsprechende Luftfahrzeuggruppe aus Tabelle A.1 verwendet.
Die Gesamtanzahl der Flugbewegungen sowie die Anzahl der Tag-, Abend- und Nachtflüge der einzelnen Luftfahrzeuggruppen sind in den Datenblättern anzugeben. Für die genannten Zeitabschnitte gelten folgende Definitionen:
Im Hinblick auf die Beurteilungszeiten Tag, Abend und Nacht ist bei Abflügen der Zeitpunkt des Starts und bei Anflügen der Zeitpunkt der Landung maßgeblich. Platzrundenflüge werden der Nachtzeit (22.00 bis 06.00 Uhr) zugerechnet, sofern Start oder Landung in dieser Beurteilungszeit stattfinden.
Geht ein Landeanflug nach Bodenberührung unverzüglich in einen Start über (touch and go), so ist dies als eine Landung und ein Start zu zählen. Ebenso ist zu verfahren, falls ein ähnliches Flugmanöver ohne Bodenberührung durchgeführt wird. Gleichzeitig von mehreren militärischen Luftfahrzeugen ausgeführte Flugbewegungen (z.B. Mehrfachstarts) sind wie zeitlich getrennte Flugbewegungen zu zählen.
Zu Abschnitt 4 "Flugbetrieb"
Für jede Ab- oder Anflugstrecke sowie Platzrunde ist ein gesondertes Datenblatt auszufüllen.
Nummer 4.1.1.4:
Die Beschreibung erfolgt abschnittsweise. Der Abschnitt Nr. 1 der Abflugstrecke beginnt am Bahnbezugspunkt. Die weiteren Abschnitte beginnen jeweils am Ende des vorhergehenden Abschnitts. Der letzte Abschnitt endet beim Verlassen des Kreises mit einem Radius von mindestens 25.000 m um den Flugplatzbezugspunkt. Dabei muss sichergestellt sein, dass die Flugstrecke mindestens 5.000 m über die größte Fluglärmkontur hinaus beschrieben ist.
Ein Abschnitt ist entweder durch eine Gerade (Spalte 2) oder durch einen Kreisbogen (Spalten 3 bis 5) darzustellen. In Spalte 3 ist bei Linkskurven der Buchstabe "L", bei Rechtskurven der Buchstabe "R" einzusetzen. Die Spalten 6 und 7 werden zur Berücksichtigung der Verteilung der Flugwege innerhalb eines Korridors verwendet. Die dargestellte Abflugstrecke gilt als Mittellinie des Korridors. Der Radius des Kreisbogens (Spalte 5) muss immer größer sein als die halbe Korridorbreite an den Abschnittsenden (Spalte 6 und 7). Falls dies nicht möglich sein sollte, muss die Strecke in mehrere Teilstrecken aufgeteilt werden, die diese Bedingung erfüllen.
Nummer 4.1.1.5:
Bei VFR-Flügen ist die geringste Flughöhe im Horizontalflug anzugeben. Beim Flugzeugschlepp ist die Flughöhe beim Ausklinken (hSchlepp) des Segelflugzeugs einzutragen.
Nummer 4.2.1.4:
Es ist der durch das Instrumenten-Landesystem (ILS), das Gleitwinkelbefeuerungssystem (z.B. Precision Approach Path Indicator, PAPI) oder ein anderes Landesystem festgelegte Gleitwinkel anzugeben. Sind diese Einrichtungen nicht vorhanden, so ist ein Gleitwinkel von 3,0° einzusetzen.
Nummer 4.2.1.5:
Die Anflugstrecken sind entgegen der Flugrichtung zu beschreiben. Die Erläuterungen zu Nummer 4.1.1.4 gelten entsprechend.
Nummer 4.2.1.7:
Bei VFR-Flügen ist die geringste Flughöhe im Horizontalflug anzugeben.
Nummer 4.3.1.3:
Für jede Startrichtung sind jeweils gesonderte Datenblätter Nummern 4.3.1 und 4.3.2 auszufüllen.
Nummer 4.3.1.5:
Die Platzrunden sind entgegen der Flugrichtung zu beschreiben. Die Erläuterungen zu Nummer 4.1.1.4 gelten entsprechend.
Nummer 4.4.1.3:
Der Steigwinkel der Hubschrauber ist nur dann in das Datenerfassungssystem einzutragen, wenn darüber fundierte Informationen vorliegen.
Nummer 4.4.1.4:
Die rechtweisende Richtung des Abschnitts Nr. 1 stimmt mit dem Abflugkurs der Hubschrauber überein.
Nummer 4.4.1.5:
Die Beschreibung erfolgt abschnittsweise. Der Abschnitt Nr. 1 der Abflugstrecke beginnt an der Hubschrauberstart- und -landestelle. Die weiteren Abschnitte beginnen jeweils am Ende des vorhergehenden Abschnitts. Der letzte Abschnitt endet beim Verlassen des Kreises mit einem Radius von mindestens 25.000 m um den Flugplatzbezugspunkt. Dabei muss sichergestellt sein, dass die Flugstrecke mindestens 5.000 m über die größte Fluglärmkontur hinaus beschrieben ist.
Ein Abschnitt ist entweder durch eine Gerade (Spalte 2) oder durch einen Kreisbogen (Spalten 3 bis 5) darzustellen. In Spalte 3 ist bei Linkskurven der Buchstabe "L", bei Rechtskurven der Buchstabe "R" einzusetzen. Die Spalten 6 und 7 werden zur Berücksichtigung der Verteilung der Flugwege innerhalb eines Korridors verwendet. Die dargestellte Abflugstrecke gilt als Mittellinie des Korridors. Der Radius des Kreisbogens (Spalte 5) muss immer größer sein als die halbe Korridorbreite an den Abschnittsenden (Spalte 6 und 7). Falls dies nicht möglich sein sollte, muss die Strecke in mehrere Teilstrecken aufgeteilt werden, die diese Bedingung erfüllen.
Nummer 4.5.1.3:
Der Gleitwinkel der Hubschrauber ist nur dann in das Datenerfassungssystem einzutragen, wenn darüber fundierte Informationen vorliegen.
Nummer 4.5.1.4:
Die Anflugstrecken sind entgegen der Flugrichtung zu beschreiben. Die rechtweisende Richtung des Abschnitts Nr. 1 der Anflugstrecke ist deshalb die entgegengesetzte Richtung des tatsächlichen Landekurses der Hubschrauber.
Nummer 4.5.1.5:
Die Erläuterungen zu Nummer 4.4.1.5 gelten entsprechend.
Nummer 4.6.1.5:
Die rechtweisende Richtung des Abschnitts Nr. 1 der Platzrunde ist die entgegengesetzte Richtung des tatsächlichen Landekurses der Hubschrauber.
Nummer 4.6.1.6:
Die Platzrunden sind - beginnend auf der Start- und Landebahn - entgegen der Flugrichtung zu beschreiben. Die Erläuterungen zu Nummer 4.4.1.5 gelten entsprechend.
Nummer 4.6.1.7:
Es ist die geringste Flughöhe im Horizontalflug anzugeben.
A.2 Anfertigung des Datenerfassungssystems
Die Datenblätter für Flugplätze sind in folgender Reihenfolge anzuordnen:
Alle weiteren Datenblätter sind ihrer Nummerierung entsprechend anzuordnen.
A.3 Qualitätssicherung der Datenerfassung
Bei der Erstellung des Datenerfassungssystems ist darauf zu achten, dass es vollständig und widerspruchsfrei ist. Es sollten insbesondere folgende Punkte berücksichtigt werden:
Zur Prüfung der im Datenerfassungssystem angegebenen Flugbewegungszahlen legt der Flugplatzhalter der zuständigen Behörde eine detaillierte Flugbewegungsstatistik in übersichtlicher Form vor. Die Statistik muss für die Zeitabschnitte Tag, Abend und Nacht mindestens folgende Angaben (absolute und prozentuale Zahlen) enthalten:
A.4 Datenblätter für Flugplätze
1 Allgemeines
| 1.1 Datum der DES-Erstellung |  |
| 1.2 Ist-Jahr |  |
2 Flugplatzdaten
2.1 Flugplatz
| Name |  |
| ICAO-Flugplatzcode |  |
2.2 Flugplatzbezugspunkt
| geographische Breite und Länge (WGS84) |  |
| UTM32/33 (ETRS89) |  |
| 2.3 Flugplatzhöhe über NN [m] |  |
2.4 Start- und Landebahnen
| I | II | III | IV | ||
| 1. | Bezeichnung | / | / | / | / |
| 2. | Vorhanden/geplant für Jahr | ||||
| 3. | rechtweisende Richtung [°] | ||||
| geographisch Nord (WGS84) | / | / | / | / | |
| Gitter-Nord UTM32/33 (ETRS89) | / | / | / | / | |
| 4. | Gesamtlänge [m] | ||||
| 5. | Koordinaten des Bahnbezugspunktes | ||||
| geographische Koordinaten (WGS84) |
N | N | N | N | |
| UTM-Koordinaten 32/33 (ETRS89) |
E | E | E | E | |
| 6. | Rechts- und Hochwertdifferenz des Bahnbezugspunktes vom Flugplatzbezugspunkt [m] | Δ R =
Δ H = |
Δ R =
Δ H = |
ΔR =
ΔH = |
Δ R =
Δ H = |
| 7. | Abstand des Startpunktes vom Bahnbezugspunkt [m] | / | / | / | / |
| 8. | Abstand der Landeschwelle vom Bahnbezugspunkt [m] | / | / | / | / |
| 9. | Abstand des Bahnanfangs vom Bahnbezugspunkt [m] | / | / | / | / |
| 10. | Meridiankonvergenz | ||||
3 Flugbewegungsangaben
3.1 Gesamtzahl der Flugbewegungen mit Flugzeugen in dem Ist-Jahr
| Luftfahrzeuggruppen | Ist | |||
| Anzahl der Flugbewegungen mit Flugzeugen | ||||
| Tag (06.00 - 18.00 Uhr) |
Abend (18.00 - 22.00 Uhr) |
Nacht (22.00 - 06.00 Uhr) |
gesamt | |
| ATD | ||||
| P 1.0 | ||||
| P 1.1 | ||||
| P 1.2 | ||||
| P 1.3 | ||||
| P 1.4 | ||||
| P 2.1 | ||||
| P 2.2 | ||||
| S 1.0 | ||||
| S 1.1 | ||||
| S 1.2 | ||||
| S 1.3 | ||||
| S 2 | ||||
| S 3.1 | ||||
| S 3.2 | ||||
| S 4 | ||||
| S 5.1 | ||||
| S 5.2 | ||||
| S 5.3 | ||||
| S 6.1 | ||||
| S 6.2 | ||||
| S 7 | ||||
| S 8 | ||||
| P-MIL 1 | ||||
| P-MIL 2 | ||||
| S-MIL 1 | ||||
| S-MIL 2 | ||||
| S-MIL 3 | ||||
| S-MIL 4 | ||||
| S-MIL 5 | ||||
| S-MIL 6 | ||||
| insgesamt | ||||
3.2 Gesamtzahl der Flugbewegungen mit Hubschraubern in dem Ist-Jahr
| Luftfahrzeuggruppen | Ist | |||
| Anzahl der Flugbewegungen mit Hubschraubern | ||||
| Tag (06.00 - 18.00 Uhr) |
Abend (18.00 - 22.00 Uhr) |
Nacht (22.00 - 06.00 Uhr) |
gesamt | |
| H 1.0 | ||||
| H 1.1 | ||||
| H 1.2 | ||||
| H 2.1 | ||||
| H 2.2 | ||||
| insgesamt | ||||
4 Flugbetrieb
4.1 Abflugstrecken mit Flugzeugen
4.1.1 Streckenbeschreibung
| 4.1.1.1 Bezeichnung |  |
| 4.1.1.2 Start- und Landebahn |  |
| 4.1.1.3 Startrichtung |  |
4.1.1.4 Beschreibung der Abflugstrecke (in Flugrichtung)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Abschnitt Nr. |
Gerade | Kurve | Korridorbreite am | |||
| Länge | L/R | Kursänderung | Radius | Anfang | Ende | |
| [m] | [°] | [m] | des Abschnitts [m] |
|||
| 4.1.1.5 Flughöhe über Platz [m] (nur für VFR-Flüge) oder beim Flugzeugschlepp die Flughöhe beim Ausklinken [m] |  |
4.1.2 Flugbewegungsangaben
| 4.1.2.1 Bezeichnung |  |
| 4.1.2.2 Start- und Landebahn |  |
| 4.1.2.3 Startrichtung |  |
4.1.2.4 Flugbewegungszahlen
| Luftfahrzeugklassen | Ist | |||
| Anzahl der Flugbewegungen mit Flugzeugen | ||||
| Tag (06.00 - 18.00 Uhr) |
Abend (18.00 - 22.00 Uhr) |
Nacht (22.00 - 06.00 Uhr) |
gesamt | |
| ATD-S | ||||
| P 1.0-S | ||||
| P 1.1-S | ||||
| P 1.2-S | ||||
| P 1.3-S | ||||
| P 1.4-S | ||||
| P 2.1-S | ||||
| P 2.2-S | ||||
| S 1.0-S | ||||
| S 1.1-S | ||||
| S 1.2-S | ||||
| S 1.3-S | ||||
| S 2-S | ||||
| S 3.1-S | ||||
| S 3.2-S | ||||
| S 4-S | ||||
| S 5.1-S | ||||
| S 5.2-S | ||||
| S 5.3-S | ||||
| S 6.1-S | ||||
| S 6.2-S | ||||
| S 7-S | ||||
| S 8-S | ||||
| P-MIL 1-S | ||||
| P-MIL 2-S | ||||
| S-MIL 1-S | ||||
| S-MIL 2-S | ||||
| S-MIL 3-S | ||||
| S-MIL 4-S | ||||
| S-MIL 5-S | ||||
| S-MIL 6-S | ||||
| insgesamt | ||||
4.2 Anflugstrecken mit Flugzeugen
4.2.1 Streckenbeschreibung
| 4.2.1.1 Bezeichnung |  |
| 4.2.1.2 Start- und Landebahn |  |
| 4.2.1.3 Landerichtung |  |
| 4.2.1.4 Gleitwinkel [°] |  |
4.2.1.5 Beschreibung der Anflugstrecke (entgegen der Flugrichtung)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Abschnitt Nr. |
Gerade | Kurve | Korridorbreite am | |||
| Länge | L/R | Kursänderung | Radius | Anfang | Ende | |
| [m] | [°] | [m] | des Abschnitts [m] |
|||
| 4.2.1.6 Zwischenanflughöhe über Platz [m] (nur für IFR-Flüge) |  |
| 4.2.1.7 Flughöhe über Platz [m] (nur für VFR-Flüge) |  |
4.2.2 Flugbewegungsangaben
| 4.2.2.1 Bezeichnung |  |
| 4.2.2.2 Start- und Landebahn |  |
| 4.2.2.3 Landerichtung |  |
4.2.2.4 Flugbewegungszahlen
| Luftfahrzeugklassen | Ist | |||
| Anzahl der Flugbewegungen mit Flugzeugen | ||||
| Tag (06.00 - 18.00 Uhr) |
Abend (18.00 - 22.00 Uhr) |
Nacht (22.00 - 06.00 Uhr) |
gesamt | |
| ATD-L | ||||
| P 1.0-L | ||||
| P 1.1-L | ||||
| P 1.2-L | ||||
| P 1.3-L | ||||
| P 1.4-L | ||||
| P 2.1-L | ||||
| P 2.2-L | ||||
| S 1.0-L | ||||
| S 1.1-L | ||||
| S 1.2-L | ||||
| S 1.3-L | ||||
| S 2-L | ||||
| S 3.1-L | ||||
| S 3.2-L | ||||
| S 4-L | ||||
| S 5.1-L | ||||
| S 5.2-L | ||||
| S 5.3-L | ||||
| S 6.1-L | ||||
| S 6.2-L | ||||
| S 7-L | ||||
| S 8-L | ||||
| P-MIL 1-L | ||||
| P-MIL 2-L | ||||
| S-MIL 1-L | ||||
| S-MIL 2-L | ||||
| S-MIL 3-L | ||||
| S-MIL 4-L | ||||
| S-MIL 5-L | ||||
| S-MIL 6-L | ||||
| insgesamt | ||||
4.3 Platzrunden mit Flugzeugen
4.3.1 Streckenbeschreibung
| 4.3.1.1 Bezeichnung |  |
| 4.3.1.2 Start- und Landebahn |  |
| 4.3.1.3 Startrichtung |  |
| 4.3.1.4 Gleitwinkel [°] |  |
4.3.1.5 Beschreibung der Platzrunde (entgegen der Flugrichtung)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Abschnitt Nr. |
Gerade | Kurve | Korridorbreite am | |||
| Länge | L/R | Kursänderung | Radius | Anfang | Ende | |
| [m] | [°] | [m] | des Abschnitts [m] |
|||
| 4.3.1.6 Flughöhe über Platz im Gegenanflug [m] |  |
4.3.2 Flugbewegungsangaben
| 4.3.2.1 Bezeichnung |  |
| 4.3.2.2 Start- und Landebahn |  |
4.3.2.3 Flugbewegungszahlen
| Luftfahrzeuggruppen | Ist | |||
| Anzahl der Flugbewegungen mit Flugzeugen | ||||
| Tag (06.00 - 18.00 Uhr) |
Abend (18.00 - 22.00 Uhr) |
Nacht (22.00 - 06.00 Uhr) |
gesamt | |
| ATD | ||||
| P 1.0 | ||||
| P 1.1 | ||||
| P 1.2 | ||||
| P 1.3 | ||||
| P 1.4 | ||||
| P 2.1 | ||||
| P 2.2 | ||||
| S 1.0 | ||||
| S 1.1 | ||||
| S 1.2 | ||||
| S 1.3 | ||||
| S 2 | ||||
| S 3.1 | ||||
| S 3.2 | ||||
| S 4 | ||||
| S 5.1 | ||||
| S 5.2 | ||||
| S 5.3 | ||||
| S 6.1 | ||||
| S 6.2 | ||||
| S 7 | ||||
| S 8 | ||||
| insgesamt | ||||
4.4 Abflugstrecken mit Hubschraubern
4.4.1 Streckenbeschreibung
| 4.4.1.1 Bezeichnung |  |
4.4.1.2 Koordinaten der Hubschrauberstart- und -landestelle (UTM32/33 (ETRS89)):
 |
 |
| 4.4.1.3 Steigwinkel [°] |  |
| 4.4.1.4 Rechtweisende Richtung des Abschnitts Nr. 1 der Abflugstrecke [°] |  |
4.4.1.5 Beschreibung der Abflugstrecke (in Flugrichtung)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Abschnitt Nr. |
Gerade | Kurve | Korridorbreite am | |||
| Länge | L/R | Kursänderung | Radius | Anfang | Ende | |
| [m] | [°] | [m] | des Abschnitts [m] |
|||
| 4.4.1.6 Flughöhe über Platz [m] |  |
4.4.2 Flugbewegungsangaben
| 4.4.2.1 Bezeichnung |  |
4.4.2.2 Flugbewegungszahlen
| Luftfahrzeuggruppen | Ist | |||
| Anzahl der Flugbewegungen mit Hubschraubern | ||||
| Tag (06.00 - 18.00 Uhr) |
Abend (18.00 - 22.00 Uhr) |
Nacht (22.00 - 06.00 Uhr) |
gesamt | |
| H 1.0-S | ||||
| H 1.1-S | ||||
| H 1.2-S | ||||
| H 2.1-S | ||||
| H 2.2-S | ||||
| insgesamt | ||||
4.5 Anflugstrecken mit Hubschraubern
4.5.1 Streckenbeschreibung
| 4.5.1.1 Bezeichnung |  |
4.5.1.2 Koordinaten der Hubschrauberstart- und -landestelle (UTM32/33 (ETRS89)):
 |
 |
| 4.5.1.3 Gleitwinkel [°] |  |
| 4.5.1.4 Rechtweisende Richtung des Abschnitts Nr. 1 der Anflugstrecke [°] |  |
4.5.1.5 Beschreibung der Anflugstrecke (entgegen der Flugrichtung)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Abschnitt Nr. |
Gerade | Kurve | Korridorbreite am | |||
| Länge | L/R | Kursänderung | Radius | Anfang | Ende | |
| [m] | [°] | [m] | des Abschnitts [m] |
|||
| 4.5.1.6 Flughöhe über Platz [m] |  |
4.5.2 Flugbewegungsangaben
| 4.5.2.1 Bezeichnung |  |
4.5.2.2 Flugbewegungszahlen
| Luftfahrzeuggruppen | Ist | |||
| Anzahl der Flugbewegungen mit Hubschraubern | ||||
| Tag (06.00 - 18.00 Uhr) |
Abend (18.00 - 22.00 Uhr) |
Nacht (22.00 - 06.00 Uhr) |
gesamt | |
| H 1.0-L | ||||
| H 1.1-L | ||||
| H 1.2-L | ||||
| H 2.1-L | ||||
| H 2.2-L | ||||
| insgesamt | ||||
4.6 Platzrunden mit Hubschraubern
4.6.1 Streckenbeschreibung
| 4.6.1.1 Bezeichnung |  |
4.6.1.2 Koordinaten der Hubschrauberstart- und -landestelle (UTM32/33 (ETRS89)):
 |
 |
| 4.6.1.3 Steigwinkel [°] |  |
| 4.6.1.4 Gleitwinkel [°] |  |
| 4.6.1.5 Rechtweisende Richtung des Abschnitts Nr. 1 der Platzrunde [°] |  |
4.6.1.6 Beschreibung der Platzrunde (entgegen der Flugrichtung)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Abschnitt Nr. |
Gerade | Kurve | Korridorbreite am | |||
| Länge | L/R | Kursänderung | Radius | Anfang | Ende | |
| [m] | [°] | [m] | des Abschnitts [m] |
|||
| 4.6.1.7 Flughöhe über Platz [m] |  |
4.6.2 Flugbewegungsangaben
| 4.6.2.1 Bezeichnung |  |
4.6.2.2 Flugbewegungszahlen
| Luftfahrzeuggruppen | Ist | |||
| Anzahl der Flugbewegungen mit Hubschraubern | ||||
| Tag (06.00 - 18.00 Uhr) |
Abend (18.00 - 22.00 Uhr) |
Nacht (22.00 - 06.00 Uhr) |
gesamt | |
| H 1.0 | ||||
| H 1.1 | ||||
| H 1.2 | ||||
| H 2.1 | ||||
| H 2.2 | ||||
| insgesamt | ||||
B Flugleistungsberechnung
B.1 Begriffe und Symbole
Die in diesem Anhang verwendeten Bezeichnungen und Symbole entsprechen dem herkömmlichen Sprachgebrauch im Bereich der Flugleistungsberechnung. Im Haupttext angegebene Größen haben hier die gleichen Symbole; einige wenige Größe werden abweichend verwendet und sind mit einem Sternchen (*) versehen. Gelegentlich stehen US-Einheiten und SI-Einheiten nebeneinander; dies geschieht im Interesse der Konventionen, die den Anwendern verschiedener Disziplinen geläufig sind.
B.1.1 Begriffe
Break-Point
"Knickpunkt", siehe Flat-Rating
Berichtigte Fluggeschwindigkeit (CAS)
Auch als kalibrierte Fluggeschwindigkeit bezeichnet. Die Geschwindigkeit des Luftfahrzeugs bezogen auf die umgebende Luft entsprechend der Anzeige eines kalibrierten Bordinstruments. Die Eigengeschwindigkeit (wahre Fluggeschwindigkeit) ist normalerweise höher und kann bei bekannter Luftdichte anhand der korrigiert angezeigten Fluggeschwindigkeit berechnet werden.
Korrigierter Nettoschub
Der Nettoschub ist die Antriebskraft, die ein Triebwerk auf die Luftfahrzeugzelle ausübt. Bei einer gegebenen Einstellung der Leistung (EPR oderN1) nimmt diese Kraft bei wachsender Höhe mit der Luftdichte ab; der korrigierte Nettoschub ist der Schub auf Höhe des Meeresspiegels.
Flat-Rating
Bei bestimmten hohen Baugruppentemperaturen kommt es mit ansteigender Umgebungslufttemperatur zu einem Abfall des Triebwerksschubs - und umgekehrt. Das bedeutet, es besteht eine kritische Lufttemperatur, bei deren Überschreiten der Nennschub nicht mehr erreicht werden kann. Bei modernen Triebwerken wird dies als "Flat-Rated Temperature" bezeichnet, da bei niedrigeren Lufttemperaturen der Schub im Interesse einer maximalen Nutzungsdauer automatisch auf Nennschub begrenzt wird. Der Schub fällt bei Temperaturen oberhalb dieser Grenztemperatur ohnehin ab. Diese Leistungsgrenze wird oft auch als "Break-Point" oder "Break-Temperatur" bezeichnet.
Geschwindigkeit
Betrag des Geschwindigkeitsvektors bezogen auf das Flugplatzkoordinatensystem.
Nennschub
Die Nutzungsdauer eines Luftfahrzeugtriebwerks hängt stark von den Betriebstemperaturen seiner Komponenten ab. Je höher die erzeugte Leistung bzw. der erzeugte Schub, desto höher die Temperaturen und desto kürzer die Lebensdauer. Um die Anforderungen an Leistung und Lebensdauer gleichermaßen zu berücksichtigen, haben leistungsangepasste ("flat-rated") Triebwerke spezielleNennwerte (Schub-Ratings) für Abheben, Steigflug und Reiseflug, mit denen maximal zulässige Leistungswerte für den Normalbetrieb festgelegt sind.
Schubeinstellungsparameter
Der Luftfahrzeugführer kann keinen speziellen Triebwerksschub anwählen, sondern wählt stattdessen eine geeignete Einstellung für diesen Parameter, der im Cockpit angezeigt wird, üblicherweise das Triebwerksdruckverhältnis (EPR) oder die Drehzahl (N1) des Niederdruckverdichters oder Fans.
B.1.2 Symbole
Kenngrößen sind dimensionslos, soweit nicht anders angegeben. Die Indizes 1 und 2 bezeichnen die am Anfang bzw. Ende eines Segments vorliegenden Bedingungen. Überstriche bezeichnen Segmentmittelwerte, d. h. den Durchschnitt von Start- und Endwerten.
Tabelle B.1: Formelzeichen, Einheiten und Bedeutung
| Formelzeichen | Einheit | Bedeutung |
| a | ft/s2 | Mittlere Beschleunigung |
| amax | ft/s2 | Maximal verfügbare Beschleunigung |
| A,B,C,D | kn/√lb | Klappenbeiwerte |
| B8 | ft/lbf | Beiwert mit Eignung für eine spezielle Kombination von Luftfahrzeug/ Klappenstellung für die ISA-Referenzbedingungen unter Einbeziehung von Gegenwind mit 8 kn |
| E, F, GA, GB, H | lb.s/ft, lb/ft, lb/ft2, lb/ °C | Triebwerksschubbeiwerte |
| Fn | lbf | Nettoschub je Triebwerk |
| Fn/δ | lbf | Korrigierter Nettoschub je Triebwerk |
| (Fn/δ)high | lbf | korrigierter Nettoschub für hohe Temperaturen |
| G | - | Steiggradient |
| G" | - | Steiggradient bei Triebwerksausfall |
| GR | - | Mittlerer Start-/Landebahngradient, positiv bei Steigung |
| g | ft/s2 | Erdbeschleunigung |
| h | ft | Druckhöhe |
| ISA | - | Internationale Standardatmosphäre |
| N * | - | Anzahl der Schub erzeugenden Triebwerke |
| N1 | % | Drehzahl der Welle von Niederdruckverdichter, Fan und Niederdruckturbine des Triebwerks |
| N1 / √θ | % | korrigierteN1-Drehzahl |
| k | ft/(s ·kn) | Konstante zur Konvertierung von Knoten in ft/s = 1,688 ft/(s ·kn) |
| K | - | geschwindigkeitsabhängige Konstante, ist 1,01 beiVc ≤ 200 kn, sonst 0,95 |
| K3, K4 | - | Konstanten, abgeleitet aus Triebwerksdaten, die dieN1-Drehzahl umfassen. |
| Pp | hp | Nettoantriebskraft für die gegebene Flugbedingung, z.B. maximale Startleistung oder maximale Steigleistung |
| r | ft | Kurvenradius |
| R | - | GleitzahlCD/CL |
| ROC | ft/min | Segment-Steigrate |
| s | ft | Zurückgelegter Weg auf dem Kurs über Grund |
| STO8 | ft | Startstrecke bei Gegenwind von 8 kn |
| STOG | ft | Nachw undGR korrigierte Startstrecke |
| STOw | ft | Startstrecke bei Gegenwindw |
| T | °C | Lufttemperatur |
| TB | °C | Break-Point-Temperatur |
| V | kn | Geschwindigkeit über Grund |
| VC | kn | Berichtigte Fluggeschwindigkeit |
| VT | kn | Wahre Fluggeschwindigkeit |
| W | lb | Luftfahrzeugmasse |
| w | kn | Gegenwindgeschwindigkeit |
| Δs | ft | Auf den Kurs über Grund projizierte Segmentlänge bei Windstille |
| Δsw | ft | Gegenwindberichtigte bodenprojizierte Segmentlänge |
| δ | - | δ = p/po, Verhältnis Außenluftdruck am Luftfahrzeug zum Normalluftdruck auf Meereshöhe:po = 1.013,25 hPa (bzw. 1.013,25 mb) |
| δ2 | - | Druckverhältnis in Höheh2 |
| ε | Radiant | Querneigungswinkel |
| γ | Radiant | Steigwinkel/Sinkwinkel |
| η | - | Propellerwirkungsgrad |
| θ | - | θ = (T + 273,15)/(To + 273,15), Verhältnis Lufttemperatur in der Höhe zur Standardlufttemperatur auf Meereshöhe:To = 15,0 °C |
| σ * | - | σ =p/po, Verhältnis Luftdichte in der Höhe zu NN-Wert (auchσ =δ/θ) |
B.2 Einführung
B.2.1 Flugbahnsynthese
In Anhang B werden Empfehlungen für Verfahren zur Berechnung des Flugprofils eines Luftfahrzeugs anhand spezifischer aerodynamischer und triebwerksbezogener Parameter, der Luftfahrzeugmasse, der atmosphärischen Bedingungen, des Kurses über Grund und des Betriebsverfahrens (Luftfahrzeugkonfiguration, Leistungseinstellung, Vorwärtsgeschwindigkeit, Vertikalgeschwindigkeit usw.) gegeben. Das Betriebsverfahren wird als Satz vonVerfahrensschritten beschrieben, mit denen vorgeschrieben wird, wie das Profil zu fliegen ist.
Das Flugprofil für Start oder Anflug wird von einer Reihe geradliniger Segmente dargestellt, deren Endpunkte alsProfilpunkte bezeichnet werden. Die Berechnung des Flugprofils erfolgt mit aerodynamischen und schubkraftbezogenen Gleichungen, die zahlreiche Koeffizienten und Konstanten enthalten, die für die spezielle Kombination von Luftfahrzeugzelle und Triebwerk bekannt sein müssen. Dieser Berechnungsprozess wird im Text alsSynthese der Flugbahn bezeichnet.
Neben den Leistungsparametern des Luftfahrzeugs, die aus der BUF-D bezogen werden können, sind für diese Gleichungen folgende Angaben erforderlich:
Das Flugprofil wird Schritt für Schritt aufgebaut, wobei die Anfangsparameter eines jeden Segments identisch mit den Endparametern des vorhergehenden Segments sind.
Die aerodynamischen Leistungsparameter in der BUF-D sollen die tatsächliche Flugbahn eines Luftfahrzeugs für die angegebenen Referenzbedingungen mit ausreichender Genauigkeit darstellen (siehe Abschnitt 8). Die Eignung der aerodynamischen Parameter und Triebwerksbeiwerte für Lufttemperaturen bis 43 °C, Flugplatzhöhen bis 4.000 ft und über einen in der BUF-D angegebenen Luftfahrzeugmassenbereich ist nachgewiesen. Die Gleichungen gestatten demnach die Berechnung von Flugbahnen für andere Bedingungen - d. h. Luftfahrzeugmasse, Windgeschwindigkeit, Lufttemperatur und Flugbahnhöhe (Luftdruck) außerhalb des Referenzbereichs - in der Regel mit ausreichender Genauigkeit für die Berechnung der Fluglärmkonturen in der Umgebung eines Flugplatzes.
Abschnitt B.5 erläutert, wie die Kurvenflugeffekte beim Steigflug berücksichtigt werden. Damit lässt sich die Querneigung bei der Berechnung der seitlichen Richtwirkungseffekte (Effekte der Triebwerksanbringung) einbeziehen. Beim Kurvenflug werden abhängig von Kurvenradius und Fluggeschwindigkeit in der Regel auch die Steiggradienten reduziert.
Die Kurvenflugeffekte im Landeanflug sind komplexer und werden nicht modelliert. Das ist jedoch bezüglich der Fluglärmkonturen vernachlässigbar.
In den Abschnitten B.6 bis B.10 wird die Methodik für die Erstellung von Abflugprofilen anhand von Beiwerten und Verfahrensschritten in der BUF-D beschrieben.
Die Abschnitte B.11 und B.12 haben die verwendete Methodik für die Erstellung von Anflugprofilen anhand von Beiwerten und Verfahrensschritten in der BUF-D zum Gegenstand.
Für die Berechnung des Nettoschubs von Strahltriebwerken bzw. Propellerantrieben sind separate Gleichungssätze vorgesehen. Sofern nicht anders angemerkt, gelten die Gleichungen für die aerodynamische Leistung eines Luftfahrzeugs für strahl- und propellergetriebene Luftfahrzeuge gleichermaßen.
Mathematische Symbole sind unter B.1.2 definiert. In allen Gleichungen müssen die Einheiten der Beiwerte, Koeffizienten und Konstanten mit den Einheiten der entsprechenden Parameter und Variablen übereinstimmen. Um Übereinstimmung mit der BUF-D zu gewährleisten, wird in diesem Anhang B den im Bereich der Flugleistungsrechnung üblichen Konventionen gefolgt: Angabe der Strecken und Höhen in Fuß (ft), Geschwindigkeit in Knoten (kn), Masse in Pound (lb), Kraft in Pound-force (korrigierter Nettoschub für hohe Temperaturen) und so weiter - auch wenn bestimmte Maße (z.B. für die Atmosphäre) in SI-Einheiten ausgedrückt werden. Werden bei der Modellierung abweichende Einheiten verwendet, sollte sehr sorgfältig darauf geachtet werden, dass bei Übernahme der Gleichungen entsprechende Umrechnungsfaktoren zur Anwendung kommen.
B.2.2 Flugbahnanalyse
In manchen Fluglärmberechnungsprogrammen werden die Flugbahninformationen nicht als Verfahrensschritte dargestellt, sondern als Positions- und Zeitkoordinaten, die gewöhnlich über die Analyse von Radardaten ermittelt werden. In diesem Fall werden die hier vorgestellten Gleichungen "umgekehrt" verwendet, d. h. die Schubparameter der Triebwerke werden aus der Bewegung des Luftfahrzeugs abgeleitet und nicht umgekehrt. Nachdem die Flugbahndaten gemittelt und auf Segmentform reduziert worden sind und jedes Segment nach Steigen oder Sinken, Beschleunigen oder Abbremsen sowie Schub- und Klappenveränderungen eingeordnet ist, handelt es sich im Allgemeinen um einen sequentiellen Vorgang, anders als bei der Synthese, wo oftmals iterative Prozesse ablaufen.
B.3 Triebwerksschub
Die von jedem Triebwerk erzeugte Antriebskraft ist eine der fünf Größen, die am Ende jedes einzelnen Flugbahnsegments festzulegen ist (neben Flughöhe über Grund, Geschwindigkeit, Leistungseinstellung und Querneigung). Der Nettoschub stellt diejenige Komponente des Bruttoschubs eines Triebwerks dar, die für den Antrieb zur Verfügung steht. Bei aerodynamischen und akustischen Berechnungen ist der Nettoschub auf Normalluftdruck auf Meereshöhe bezogen. Dies wird alskorrigierter NettoschubFn/δ bezeichnet.
Das ist entweder der Nettoschub, der verfügbar ist, wenn mit einem vorgegebenenSchub-Rating gearbeitet wird, oder der Nettoschub, der sich ergibt, wenn derSchubeinstellungsparameter auf einen bestimmten Wert gesetzt wird. Für ein Turbojet- oder Turbofantriebwerk, das mit einem spezifischen Schub-Rating arbeitet, ergibt sich der korrigierte Nettoschub aus der Gleichung
| Fn/δ = E + F · VC + GA · h+ GB · h2 H · T, | ( B.1) |
wobei Folgendes gilt:
| Fn | Nettoschub je Triebwerk in lbf, |
| δ | Verhältnis von Außenluftdruck am Luftfahrzeug zum Normalluft-druck auf Meereshöhe, d. h. zu 1.013,25 hPa (oder 1.013,25 mb), |
| Fn/δ | korrigierter Nettoschub je Triebwerk in lbf, |
| VC | berichtigte Fluggeschwindigkeit in kn, |
| T | Außenlufttemperatur, die das Luftfahrzeug umgibt in °C und |
| E, F, GA, GB, H | Schubkonstanten oder Schubbeiwerte für Temperaturen unterhalb (E, F, GA, GB, H)low oder oberhalb (E, F, GA, GB, H)high der Flat-Rating-Temperatur des Triebwerks bei verwendetem Schub-Rating (am aktuellen Segment der Flugbahn für Start/Steigflug bzw. Anflug) in lb.s/ft lb/ft , lb/ft2, lb/ °C ; Werte können aus der BUF-D entnommen werden. |
In der BUF-D werden auch Daten bereitgestellt, die die Berechnung des Schubs in Abhängigkeit von einem Schubeinstellungsparameter ermöglichen. Dies wird von einigen Herstellern als TriebwerksdruckverhältnisEPR (Engine Pressure Ratio), von anderen als "Low-Pressure Rotor Speed" oder DrehzahlN1 bezeichnet. Wenn der Parameter das DruckverhältnisEPR ist, wird Gleichung ( B.1) ersetzt durch
| Fn / δ = E + F · VC + GA · h + GB · h2 + H · T + K1 · EPR + K2 · EPR2, | ( B.2) |
wobeiK1 undK2 Koeffizienten aus der BUF-D, die den korrigierten Nettoschub und das Triebwerksdruckverhältnis im Bereich des für die vorgegebene Machzahl des Luftfahrzeugs interessierenden Triebwerksdruckverhältnisses verknüpfen.
Wenn dieN1-Drehzahl als Schubeinstellungsparameter verwendet wird, sieht die verallgemeinerte Schubgleichung wie folgt aus:
| Fn / δ = E + F · VC + GA · h + GB · h2 + H · T + K3(N1 / √θ) +K4(N1 / √θ)2 , | ( B.3) |
wobei Folgendes gilt:
| N1 | Drehzahl der Welle von Niederdruckverdichter, Fan und Niederdruckturbine des Triebwerks in %, |
| θ | Verhältnis der absoluten Gesamttemperatur am Triebwerkseinlass zur absoluten Standardlufttemperatur auf Meereshöhe, |
| N1 / √θ | korrigierteN1-Drehzahl in %, |
| K3, K4 | Konstanten, abgeleitet aus Triebwerksdaten, die dieN1-Drehzahl umfassen. |
Nicht jeder Term in den Gleichungen ( B.1), ( B.2) und ( B.3) ist in jedem Falle erheblich. So kann sich beispielsweise für Flat-Rated-Triebwerke der Temperatur-Term erübrigen, wenn die Lufttemperatur unterhalb des Break-Points (typischerweise 30 °C) liegt. Bei Triebwerken ohne Flat-Rating ist bei der Schubbemessung die Umgebungstemperatur zu berücksichtigen. Oberhalb der Flat-Rating-Temperatur des Triebwerks müssen für die Bestimmung des verfügbaren Schubs andere Koeffizienten (E, F, GA, GB undH)high verwendet werden. Die normale Vorgehensweise wäre dann, dassFn/δ mit Hilfe sowohl unterer als auch oberer Temperaturbeiwerte berechnet wird und der höhere Schubwert für Temperaturenunter der Flat-Rating-Temperatur und der kleinere berechnete Schubwert für Temperaturenüber der Flat-Rating-Temperatur benutzt wird.
Soweit nur Schubbeiwerte für den unteren Temperaturbereich vorliegen, kann das folgende Verhältnis verwendet wird:
| (Fn / δ)high =F · VC + (E + H · TB) · [(1 - 0,006· T) / (1 - 0,006· TB)] | ( B.4) |
wobei Folgendes gilt:
| (Fn / δ)high | korrigierter Nettoschub für hohe Temperaturen in lbf, |
| TB | Break-Point-Temperatur (falls kein definitiver Wert vorhanden, ist ein Standardwert von 30 °C anzusetzen). |
Die BUF-D enthält Werte für die Konstanten und Koeffizienten (Beiwerte) der Gleichungen ( B.1) bis (B.4).
Für propellergetriebene Luftfahrzeuge sollte der korrigierte Nettoschub des jeweiligen Triebwerks aus Diagrammen abgelesen oder mit folgender Gleichung berechnet werden:
 |
( B.5) |
wobei Folgendes gilt:
| η | Propellerwirkungsgrad einer gegebenen Art der Propelleranbringung und in Abhängigkeit von Propellerdrehzahl und Fluggeschwindigkeit des Luftfahrzeugs, |
| VT | wahre Fluggeschwindigkeit in kn, |
| Pp | Nettoantriebskraft für die gegebene Flugbedingung, z.B. maximale Startleistung oder maximale Steigleistung in hp. |
Die Parameter in Gleichung ( B.5) werden in der BUF-D für die Einstellungen des maximalen Startschubs und des maximalen Steigschubs bereitgestellt.
Die wahre FluggeschwindigkeitVT wird anhand der berichtigten FluggeschwindigkeitVC nach folgender Beziehung schätzungsweise ermittelt:
| VT = (VC / √σ) , | ( B.6) |
wobei σ das Verhältnis der Luftdichte am Luftfahrzeug zum Wert auf Höhe über NN ist.
B.3.1 Hinweise zum Arbeiten mit vermindertem Startschub
Es kommt nicht selten vor, dass die Startmasse eines Luftfahrzeugs geringer ist als die zulässige Startmasse und/oder die verfügbare Startbahnlänge die für den maximalen Startschub erforderliche Mindestlänge überschreitet. In solchen Fällen hat es sich in der Praxis durchgesetzt, dass der Triebwerksschub im Interesse einer längeren Lebensdauer der Triebwerke und teilweise auch aus Lärmschutzgründen auf Werte unter Maximum reduziert wird. Der Triebwerksschub kann nur soweit herabgesetzt werden, wie dies die Sicherheit nicht gefährdet. Das von Luftverkehrsgesellschaften verwendete Berechnungsverfahren zur Bestimmung des Schubreduzierungsbetrags ist dementsprechend reguliert: das Verfahren ist komplex und berücksichtigt zahlreiche Faktoren wie Startmasse, Außenlufttemperatur, gemeldete Startbahnstrecken, Startbahnhöhe und Kriterien der Hindernisfreiheit. Deshalb variiert die Schubreduzierung von Flug zu Flug.
Da die Auswirkungen auf die Fluglärmkonturen im Startbereich erheblich sein können, sollten die Schubreduzierungen bei der Modellierung angemessen berücksichtigt werden. Daher sollten Luftverkehrsgesellschaften hierzu befragt werden.
Eine direkte Übernahme der betriebstechnischen Berechnungen in die Lärmmodellierung ist unpraktisch und wäre angesichts der üblichen Vereinfachungen und Näherungen, die zur Berechnung langfristiger durchschnittlicher Schallpegel vorgenommen werden, auch nicht zweckdienlich. Die folgenden Hinweise bieten eine praktikable Alternative.
Wie die Analyse der Daten von Flugdatenschreibern gezeigt hat, ist der Grad der Schubreduzierung stark an das Verhältnis der tatsächlichen Startmasse zur zulässigen Startmasse (MATOM) geknüpft, bis hin zu einem festen unteren Grenzwert 17; d. h.
| Fn / δ = (Fn / δ)max(W/WMATOM) , | ( B.7) |
wobei Folgendes gilt:
| (Fn / δ)max | maximaler Nennschub, |
| W | tatsächliche Bruttostartmasse und |
| WMATOM | zulässige Startmasse. |
Die zulässige Startmasse ist die Startmasse, die unter Einhaltung der Startstreckenlänge sowie Triebwerksausfall- und Hindernisanforderungen gefahrlos eingesetzt werden kann. Sie ist abhängig von verfügbarer Startbahnlänge, Flugplatzhöhe, Temperatur, Gegenwind und Klappenstellung. Diese Informationen können bei den Luftverkehrsgesellschaften eingeholt werden und dürften einfacher erhältlich sein als Angaben über tatsächliche Schubreduzierungen. Die zulässige Startmasse kann alternativ dazu mit Daten aus Flughandbüchern berechnet werden.
B.3.2 Reduzierter Steigschub
Wenn Luftverkehrsgesellschaften mit reduziertem Startschub arbeiten, setzen sie oft, den Steigschub im Verhältnis zum Maximum herunter 18. Damit wird Situationen vorgebeugt, in denen am Ende des mit Startschub vorgenommenen Anfangssteigflugs die Leistung erhöht werden muss, statt dass sie zurückgenommen wird. Hier lässt sich jedoch eine gemeinsame Basis schwieriger formulieren. Einige Luftverkehrsgesellschaften verwenden unterhalb des maximalen Steigschubs feste Stufen, die manchmal als Steigstufe 1 und Steigstufe 2 bezeichnet werden und den Steigschub typischerweise um 10 % bzw. 20 % gegenüber dem Maximum reduzieren. Es wird empfohlen, bei Verwendung eines reduzierten Startschubs auch die Steigschubwerte um 10 % zu reduzieren.
B.4 Vertikalprofile von Lufttemperatur, Luftdruck, Luftdichte und Windgeschwindigkeit
Im Rahmen dieses Dokuments wird davon ausgegangen, dass die höhenabhängigen Temperatur-, Druck- und Dichteschwankungen entsprechend der internationalen Standardatmosphäre auf die Höhe über Normalnull bezogen sind. Die nachstehend beschriebenen Methoden sind für Flugplatzhöhen bis zu 4.000 ft über Meereshöhe und für Lufttemperaturen bis zu 43 °C (109 °F) bestätigt.
Im Folgenden angegebene Flugleistungsgleichungen beruhen auf der allgemeinen Annahme, dass das Luftfahrzeug jederzeit direkt in einen (Standard-)Gegenwind von 8 kn hineinsteuert - unabhängig vom Kompasskurs. Es werden Methoden zur Anpassung der Ergebnisse an andere Gegenwindgeschwindigkeiten angeboten.
B.5 Kurvenflugeffekte
In den restlichen Abschnitten dieses Anhangs werden die methodischen Ansätze zur Berechnung der erforderlichen Eigenschaften der Segmente beschrieben, die die Profilpunktes, z verbinden und die zweidimensionale Flugbahn in der vertikalen Ebene über dem Kurs über Grund definieren. Die Reihenfolge der Segmente folgt der Bewegungsrichtung. Am Ende eines jeden Segments (bzw. am Anfang der Rollbewegung im Falle des ersten Segments einer Abflugsequenz), wo die Betriebsparameter und der nächste Verfahrensschritt festgelegt werden, müssen Steigwinkel und zurückgelegte Strecke bis zu dem Punkt, an dem die erforderliche Höhe und/oder Geschwindigkeit erreicht wird, berechnet werden.
Bei gerader Flugtrecke wird hierzu ein einzelnes Profilsegment verwendet, dessen Geometrie dann direkt (teilweise aber auch mit iterativem Anteil) bestimmt werden kann. Falls jedoch eine Kurve beginnt oder endet oder sich der Radius bzw. die Richtung der Kurve ändert, bevor die geforderten Endbedingungen erreicht sind, wäre ein Einzelsegment unzureichend, da sich Auftrieb und Luftwiderstand des Luftfahrzeugs mit der Querneigung ändern. Zur Berücksichtigung der Kurveneffekte beim Steigflug sind für die Umsetzung des Verfahrensschrittes zusätzliche Profilsegmente erforderlich. Die Erzeugung des Kurses über Grund ist im Abschnitt 15 beschrieben. Dies geschieht unabhängig vom Flugprofil eines Luftfahrzeugs (wenn auch sichergestellt werden muss, dass keine unter normalen operativen Bedingungen nicht fliegbaren Kursänderungen definiert werden). Da aber Flugprofile (Höhe und Geschwindigkeit als Funktion der Position entlang des Kurses) durch Kursänderungen beeinflusst werden, kann das Flugprofil nicht unabhängig vom Kurs über Grund festgelegt werden.
Um in einem Kurvenflug die Geschwindigkeit zu halten, muss der aerodynamische Auftrieb des Flügels so erhöht werden, dass Fliehkraft und Gravitationskraft ausgeglichen sind. Das erhöht jedoch den Widerstand und demzufolge den erforderlichen Antriebsschub. Die Effekte des Kurvenflugs werden in Abhängigkeit vom Querneigungswinkelε ausgedrückt, der für ein Luftfahrzeug, das im Horizontalflug mit konstanter Geschwindigkeit auf einer kreisförmigen Kurvenbahn fliegt, wie folgt gegeben ist:
| ε = arctan[(2,85· V2) / (r·g)] , | ( B.8) |
wobei Folgendes gilt:
| V | Geschwindigkeit über Grund in kn, |
| r | Kurvenradius in ft, |
| g | Erdbeschleunigung in ft/s2. |
Für alle Kurven wird ein konstanter Radius angenommen, während Effekte zweiter Ordnung aus nichthorizontalen Flugbahnen außer Acht gelassen werden; die Querneigungswinkel beruhen ausschließlich auf dem Kurvenradiusr des Kurses über Grund.
Zur Umsetzung eines Verfahrensschritts wird mit Hilfe des am Anfangspunkt bestehenden Querneigungswinkelsε - wie in Gleichung ( B.8) für den Streckensegmentradiusr definiert - ein vorläufiges Profilsegment berechnet. Falls die berechnete Länge des vorläufigen Segments weder den Anfangspunkt noch den Endpunkt einer Flugkurve kreuzt, wird das vorläufige Segment bestätigt und mit dem nächsten Schritt fortgefahren.
Falls aber das vorläufige Segment einen oder mehrere Start- oder Endpunkte von Kurven kreuzt (mit Änderung vonε) 19, werden die Flugparameter am ersten entsprechenden Punkt per Interpolation ermittelt und gemeinsam mit dessen Koordinaten als Endpunktwerte abgespeichert und das Segment entsprechend abgeschnitten. Der zweite Teil des Verfahrensschritts beginnt dann am besagten Punkt - wobei vorläufig wieder davon ausgegangen wird, dass dieser Teilschritt mit den gleichen Endbedingungen, aber mit neuem Anfangspunkt und neuem Querneigungswinkel, in einem einzigen Segment abgeschlossen werden kann. Falls dieses zweite Segment auf eine weitere Änderung des Radius bzw. der Richtung der Kurve stößt, ist ein drittes Segment nötig - und so weiter bis zum Erreichen der Endbedingungen.
B.5.1 Näherungsverfahren
Es ist offensichtlich, dass Berechnungen unter Berücksichtigung aller Effekte im Kurvenflug sehr komplex sind, da das Steigflugprofil jedes Luftfahrzeuges individuell für jeden Kurs über Grund berechnet werden muss. Änderungen im Vertikalprofil, die durch Kurswechsel verursacht werden, haben im Allgemeinen einen deutlich geringeren Einfluss auf die Fluglärmkonturen als die Änderungen der Querneigung, so dass der Einfluss von Kursänderungen vernachlässigt werden kann. Demgegenüber wird die Querneigung bei der Berechnung der seitlichen Dämpfung weiterhin berücksichtigt. Unter dieser Vereinfachung werden Profilpunkte eines Flugmanövers nur einmal berechnet, indem ein gerader Kurs über Grund (ε = 0) angenommen wird.
B.6 Startrollstrecke
Der Startschub beschleunigt das Luftfahrzeug auf der Startbahn bis zum Abheben. Die berichtigte Fluggeschwindigkeit wird dann für die gesamte Anfangsphase des Steigflugs als konstant angenommen. Es wird angenommen, dass das Fahrwerk, sofern es einziehbar ist, kurz nach dem Abheben eingezogen wird.
Im Rahmen dieses Dokuments wird die tatsächliche Startrollstrecke annäherungsweise durch eine äquivalente Startstrecke (mit Standard-Gegenwind von 8 kn),ST08 bestimmt. Diese ist gemäß Abbildung B.1 definiert als die auf der Startbahn gelegene Entfernung ab dem Lösen der Bremsen bis zu dem Punkt, an dem eine geradlinige Verlängerung der mit eingezogenem Fahrwerk vollzogenen anfänglichen Steigflugbahn die Startbahn schneidet.
Abbildung B.1: Äquivalente Startstrecke

Für eine waagerechte Startbahn wird die äquivalente Startrollstrecke STO8 in Fuß anhand der folgenden Gleichung berechnet:
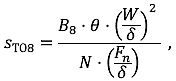 |
( B.9) |
wobei Folgendes gilt:
| B8 | Beiwert mit Eignung für eine spezielle Kombination von Luftfahrzeug/Klappenstellung für die ISA-Referenzbedingungen unter Einbeziehung von Gegenwind mit 8 kn in ft/lbf, |
| W | Luftfahrzeugbruttomasse bei Lösen der Bremsen in lbf, |
| N | Anzahl Schub erzeugender Triebwerke. |
ANMERKUNG: Da mit der Gleichung ( B.9) der unterschiedliche Schub in Abhängigkeit von Fluggeschwindigkeit und Startbahnhöhe berücksichtigt wird, hängt der Beiwert B8 für ein gegebenes Luftfahrzeug allein von der Klappenstellung ab.
Bei Gegenwind, der nicht der Standardgeschwindigkeit von 8 kn entspricht, wird die Startrollstrecke wie folgt korrigiert:
| STOw =STO8[(VC - w)2 / (VC - 8)2] , | ( B.10) |
wobei Folgendes gilt:
| STOw | Startrollstrecke korrigiert in Bezug auf Gegenwindw, ft, |
| VC | (in dieser Gleichung) berichtigte Geschwindigkeit bei Startrotation in kn, |
| w | Gegenwind in kn. |
Die Startrollstrecke wird auch in Bezug auf den Startbahngradienten korrigiert:
| STOG =STOw[a / (a - g·GR] , | ( B.11) |
wobei Folgendes gilt:
| STOG | in Bezug auf Gegenwind und Startbahngradient korrigierte Startrollstrecke in ft, |
| a | mittlere Beschleunigung auf der Startbahn, gleich (VC · √σ)2 /(2 ·STOw) in ft/s2 |
| GR | Startbahngradient; positiv bei Steigung in Startrichtung. |
B.7 Steigflug mit konstanter Geschwindigkeit
Dieser Segmenttyp wird durch die berichtigte Fluggeschwindigkeit des Luftfahrzeugs, die Klappeneinstellung und durch die Höhe und den Querneigungswinkel am Segmentende im Zusammenspiel mit der Gegenwindgeschwindigkeit (Standardwert 8 kn) definiert. Wie bei jedem Segment sind die Parameter am Segmentanfang, darunter der korrigierte Nettoschub, identisch mit den Parametern vom Ende des vorhergehenden Segments - es kommen keine Unstetigkeiten vor (außer bei Klappenwinkel und Querneigungswinkel, für die in diesen Berechnungen sprunghafte Änderungen zulässig sind). Die Nettoschubwerte des Segmentendes werden zuerst mit der zutreffenden Gleichung aus ( B.1) bis (B.5) berechnet. Der durchschnittliche geometrische Steigwinkelγ (siehe Abbildung B.1) ergibt sich dann durch
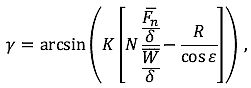 |
( B.12) |
Dabei gilt:
die Überstriche bezeichnen Segmentmittelwerte (Durchschnitt aus Startpunkt- und Endpunktwerten - in der Regel Werte aus der Segmentmitte)
| K | und geschwindigkeitsabhängige Konstante, ist 1,01 beiVC 200 ≤ kn oder sonst 0,95. Diese Konstante berücksichtigt die Auswirkungen auf den Steiggradienten bei 8 kn Gegenwind und die Beschleunigung bei einem Steigflug mit konstanter berichtigter Fluggeschwindigkeit, |
| R | Verhältnis von Widerstandsbeiwert zu Auftriebsbeiwert des Luftfahrzeugs entsprechend der gegebenen Klappenstellung. Das Fahrwerk wird als eingefahren angenommen, |
| ε | Querneigungswinkel, Radiant. |
Der Steigwinkel wird um den Gegenwindw wie folgt korrigiert:
| γw = γ[(VC - 8) / (VC - w")] | ( B.13) |
wobeiγw der mittlere gegenwindbereinigte Steigwinkel ist.
Die Wegstrecke Δs, die das Luftfahrzeug über Grund zurücklegt, während es in einem Winkel vonγw von der Höheh1 zur nächsten Höheh2 aufsteigt, ergibt sich durch
| Δs =[(h2 - h1) / tanγw] | ( B.14) |
In der Regel wird in zwei getrennten Phasen eines Abflugprofils mit konstanter Fluggeschwindigkeit geflogen. Die erste Phase, die zuweilen alsAnfangssteigflug bezeichnet wird, beginnt unmittelbar nach dem Abheben, wo aus Gründen der Sicherheit die Fluggeschwindigkeit des Luftfahrzeugs mindestens der sicheren Steigfluggeschwindigkeit entsprechen muss. Dies ist eine vorgeschriebene Geschwindigkeit und muss bei Normalstart spätestens in einer Höhe von 35 ft über der Startbahn erreicht werden. Es ist jedoch allgemeine Praxis, im Anfangssteigflug eine Geschwindigkeit zu fliegen, die etwas höher, und zwar 10-20 kn höher, als die sichere Steigfluggeschwindigkeit ist, was für einen tendenziell besseren Steiggradienten in dieser Anfangsphase sorgt. Die zweite Phase beginnt nach dem Einfahren der Klappen und der Anfangsbeschleunigung und wird alsSteigflug bezeichnet.
Im Anfangssteigflug hängt die Fluggeschwindigkeit von der Stellung der Startklappen und von der Bruttomasse des Luftfahrzeugs ab. Die berichtigte Anfangssteiggeschwindigkeit VCTO wird in erster Näherung wie folgt berechnet:
| VCTO =C√W , | ( B.15) |
wobeiC ein Beiwert für die Klappeneinstellung (kn/√lb) ist, der aus der BUF-D ausgelesen wird.
BeimSteigflug nach erfolgter Beschleunigung ist die berichtigte Fluggeschwindigkeit ein vom Anwender eingegebener Parameter.
B.8 Schubrücknahme (Übergangssegment)
Der Schub wird an einem bestimmten Punkt nach dem Start reduziert bzw. gedrosselt (Cutback), um die Triebwerke zu schonen und oft auch um in bestimmten Gebieten den Lärmpegel zu reduzieren. Die Schubreduzierung erfolgt normalerweise entweder in einem mit konstanter Geschwindigkeit geflogenen Steigflugsegment ( Abschnitt B.7) oder in einem Beschleunigungssegment ( Abschnitt B.9). Da es sich um einen relativ kurzen Vorgang handelt, der in der Regel nur 3 bis 5 Sekunden dauert, wird die Schubrücknahme dadurch modelliert, dass dem Primärsegment ein "Übergangssegment" angefügt wird. Dies erfolgt gewöhnlich für eine Bodendistanz von 1.000 ft (305 m).
B.8.1 Betrag der Schubreduzierung
Im Normalbetrieb wird der Schub des Triebwerks auf die Einstellung für maximalen Steigschub abgesenkt. Anders als der Startschub kann der Steigschub beliebig lang gehalten werden, in der Praxis üblicherweise bis zum Erreichen der ersten Reiseflughöhe des Luftfahrzeugs. Der maximale Steigschub bestimmt sich aus Gleichung ( B.1) mit Hilfe der vom Hersteller bereitgestellten maximalen Schubbeiwerte. Aus Gründen des Lärmschutzes kann jedoch eine zusätzliche Schubreduzierung erforderlich werden, die auch als "Deep Cutback" bezeichnet wird. Aus Sicherheitsgründen ist die maximale Schubreduzierung auf einen Betrag begrenzt, der sich aus der Flugleistung und der Triebwerkzahl bestimmt. Diese Untergrenze der Schubreduzierung wird manchmal auch als Engine-Out-Schubreduzierung bezeichnet:
 |
( B.16) |
wobei Folgendes gilt:
| δ2 | Druckverhältnis in Höheh2, |
| G" | Steiggradient bei Triebwerksausfall in Prozent:
0 % für Luftfahrzeuge mit ATR-Schubautomatik, |
B.8.2 Steigflugsegment mit konstanter Geschwindigkeit und Schubreduzierung
Der Gradient des Steigflugsegments wird mit Gleichung ( B.12) berechnet, wobei der Schub entweder nach Gleichung ( B.1) mit Maximalsteigungsbeiwerten oder bei reduziertem Schub nach Gleichung ( B.16) berechnet wird. Das Steigflugsegment wird anschließend in zwei Teilsegmente aufgeteilt, die den gleichen Steigwinkel aufweisen. Das ist in Abbildung B.2 illustriert.
Abbildung B.2: Steigflugsegment mit konstanter Geschwindigkeit und Schubreduzierung (Abbildung nicht maßstabsgetreu)

Dem ersten Teilsegment wird eine Strecke über Grund von 1.000 ft (305 m) zugewiesen, und der korrigierte Nettoschub am Ende der 1.000 ft wird auf den Wert der Schubreduzierung gesetzt. Wenn die ursprüngliche horizontale Entfernung kleiner als 2.000 ft ist, wird eine Hälfte des Segments für die Schubreduzierung verwendet. Der Endschub am zweiten Teilsegment wird auch auf den Wert der Schubreduzierung gesetzt. Damit wird das zweite Teilsegment mit konstantem Schub geflogen.
B.9 Beschleunigter Steigflug und Einfahren der Klappen
An den Anfangssteigflug schließt sich gewöhnlich ein beschleunigter Steigflug und das Einfahren der Klappen an. Wie bei allen Flugsegmenten sind die Werte für Anfangshöheh1, wahre FluggeschwindigkeitVT1 und Schub (Fn / δ))1 identisch mit den Endwerten des vorherigen Segments. Die berichtigte FluggeschwindigkeitVC2 und die mittlere Steigrate ROC am Endpunkt sind Anwendereingaben (Querneigungswinkelε ist abhängig von Kurvengeschwindigkeit und Kurvenradius). Aufgrund der wechselseitigen Abhängigkeit müssen die Endwerte der Höheh2, der wahren FluggeschwindigkeitVT2(h) und des Schubs (Fn / δ)2(h) sowie die Segmentstreckenlängesseg durch Iteration berechnet werden. Die Endhöhe h2 wird eingangs geschätzt und anschließend mit den Gleichungen ( B.17) und ( B.18) wiederholt neuberechnet, bis die Differenz zwischen aufeinanderfolgenden Schätzungen kleiner ist als eine entsprechend vorgegebene Toleranz, z.B. 1 ft.
Eine praktikable Anfangsschätzung isth2 =h1 + 250 ft .
Die Ermittlung der Segmentstreckenlängesseg (zurückgelegte horizontale Entfernung) erfolgt durch folgende Gleichung:
| sseg =[ (0,95k2 (V2T2 - V2T1)) / (2(amax -Gg) ] , | ( B.17) |
wobei Folgendes gilt:
| 0,95 | Faktor zur Berücksichtigung des Einflusses des Gegenwinds von 8 kn beim Steigen mit 160 kn, |
| k | Konstante zur Konvertierung von Knoten in ft/s = 1,688 ft/s pro kn, |
| VT2 | wahre Fluggeschwindigkeit am Segmentende in kn. Es giltVT2 = VC2 / √σ2 , wobeiσ2 das Luftdichteverhältnis in Endhöhe h2 ist, |
| amax | maximale Beschleunigung im Horizontalflug (ft/s2). Es gilt |
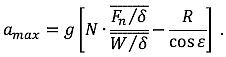 |
|
| G | Steiggradient. Es giltG ≈ ROC / (60kVT) , wobeiROC die Steigrate in ft/min ist. |
Mit Hilfe dieses Schätzwertes für sseg wird daraufhin die Endhöheh"2 nach folgender Gleichung neu bestimmt:
| h"2 =h1 + (ssegG / 0,95) . | ( B.18) |
Liegt der Fehler |h'2 =h2 | außerhalb der vorgegebenen Toleranz, werden die Schritte zur iterativen Bestimmung der aktuellen Segment-Endwerte für die Höheh2, die wahre FluggeschwindigkeitVT2 und den korrigierten Nettoschub je Triebwerk (Fn /δ)2 mit den Gleichungen ( B.17) und ( B.18) wiederholt. Sobald der Fehler im Toleranzbereich liegt, wird der iterative Zyklus beendet und das Beschleunigungssegment bestimmt sich durch die letzten Segment-Endwerte.
ANMERKUNG: Falls während des Iterationsprozesses der Fall (amax -G · g) < 0,02 g eintritt, ist die Beschleunigung unter Umständen zu klein, um die gewünschte GeschwindigkeitVC2 in einer angemessenen Entfernung zu erreichen. In diesem Fall kann der Steiggradient aufG =amax/g - 0,02 begrenzt und so die gewünschte Steigrate reduziert werden, um eine akzeptable Beschleunigung aufrechtzuerhalten. FallsG < 0,01 ist, ist nicht genügend Schub vorhanden, um die angegebene Beschleunigung und Steiggeschwindigkeit zu erreichen. Die Berechnung sollte daraufhin beendet und die Verfahrensschritte geändert werden 20.
Die Länge des Beschleunigungssegments Δsw wird entsprechend dem Gegenwindw wie folgt korrigiert:
| Δsw = Δs ((VT - w) / (VT - 8)) . | ( B.19) |
B.9.1 Beschleunigungssegment mit Schubreduzierung
Die Einrechnung der Schubreduzierung erfolgt hier genauso wie bei einem Segment mit Konstantgeschwindigkeit, wozu die Umwandlung seines ersten Teils in ein Übergangssegment erfolgt. Der Schubreduzierungswert wird wie im Schubreduzierungsverfahren für Konstantgeschwindigkeit berechnet, und zwar nur nach Gleichung ( B.1). Es ist anzumerken, dass es in der Regel nicht möglich ist, zu beschleunigen und den Steigflug durchzuführen, während die Schubeinstellung auf Engine-Out-Minimum steht. Dem Schubübergang wird eine Strecke über Grund von 305 m (1.000 ft) zugewiesen und der korrigierte
Nettoschub am Ende der 1.000 ft auf den Wert der Schubreduzierung gesetzt. Die Geschwindigkeit für das Ende des Segments wird für eine Segmentlänge von 1.000 ft per Iteration bestimmt. Wenn die ursprüngliche horizontale Entfernung kleiner als 2.000 ft ist, wird eine Hälfte des Segments für die Schubänderung verwendet. Der Endschub am zweiten Teilsegment wird auch auf den Wert der Schubreduzierung gesetzt. Damit wird das zweite Teilsegment mit konstantem Schub geflogen.
B.10 Zusätzliche Steig- und Beschleunigungssegmente nach Einfahren der Klappen
Enthält die Bahn, in der der Steigflug beginnt, zusätzliche Beschleunigungssegmente, so wird erneut mit den Gleichungen ( B.12) bis (B.19) gearbeitet, um die Länge des Kurses über Grund, den mittleren Steigwinkel und den jeweiligen Höhenzuwachs zu berechnen. Wie zuvor ist die abschließende Höhe des Segments mittels Iteration zu bestimmen.
B.11 Sinkflug und Verzögerung
Beim Anflug sinkt das Luftfahrzeug und reduziert die Geschwindigkeit, um den Endanflug vorzubereiten, in dem es durch die Betätigung der Landeklappen und das Ausfahren des Fahrwerks konfiguriert wird. Flugmechanisch gibt es keine Änderungen gegenüber dem Abflug; der Hauptunterschied besteht darin, dass das Höhen- und Geschwindigkeitsprofil grundsätzlich bekannt ist und hier für jedes Segment der Triebwerksschub bestimmt werden muss. Die grundlegende Kräftebilanzgleichung lautet:
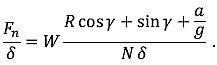 |
( B.20) |
Gleichung ( B.20) kann auf zweierlei Art verwendet werden. Zuerst können die Fluggeschwindigkeiten am Anfang und am Ende eines Segments zusammen mit einem Sinkwinkel (oder einer horizontalen Segmentdistanz) sowie mit Anfangs- und Endhöhe des Segments bestimmt werden. In diesem Fall kann die Geschwindigkeitsreduzierung (Verzögerung) nach folgender Gleichung berechnet werden:
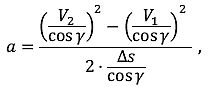 |
( B.21) |
wobei Folgendes gilt:
| Δs | ist der überflogene Kurs über Grund; |
| V1 undV2 | sind die Horizontalkomponenten der Geschwindigkeiten über Grund am Segmentanfang bzw. Segmentende. |
V1 undV2 werden nach folgender Gleichung berechnet:
| V = (Vccosγ /Ös) -w | ( B.22) |
Die Gleichungen ( B.20), ( B.21) und ( B.22) sind anwendbar, wenn die Verzögerung über eine bestimmte Strecke konstant bleibt. Stärkerer Gegenwind erfordert mehr Schub, um die Verzögerung konstant zu halten, während Rückenwind einen geringeren Schub zur Einhaltung konstanter Verzögerung erfordert.
In der Praxis erfolgen die meisten, wenn nicht alle Verzögerungen im Anflug mit Leerlaufschub. Für die Zweitanwendung der Gleichung ( B.20) ist der Schub also als Leerlaufschub definiert. Die Gleichung wird iterativ gelöst, um 1) die Verzögerung und 2) die Höhe am Ende des Verzögerungssegments zu bestimmen. In diesem Fall kann der Verzögerungsweg je nach Gegenwind und Rückenwind sehr unterschiedlich sein und mitunter ist für vertretbare Ergebnisse eine Verminderung des Sinkwinkels notwendig.
Der Leerlaufschub wird folgendermaßen berechnet:
| (Fn/δ)idle =Eidle +Fidle · VC +GA,idle · h +GB,idle · h2 +Hidle · T , | ( B.23) |
wobeiEidle ,Fidle ,GA,idle ,GB,idle undHidle Leerlaufschub-Triebwerksbeiwerte sind, die in der BUF-D stehen.
B.12 Landeanflug
Die berichtigte LandeanfluggeschwindigkeitVCA ist über eine Gleichung ähnlich ( B.15) an die Bruttolandemasse geknüpft:
| VCA ≈ D√W , | ( B.24) |
wobei der BeiwertD (kn / √lb) der Landeklappenstellung entspricht.
Zur Berechnung des durchschnittlichen korrigierten Nettoschubs je Triebwerk während des Sinkflugs auf dem Anfluggleitweg bei 8 kn Gegenwind wird Gleichung ( B.12) unter Verwendung vonK = 1,03 umgestellt:
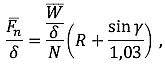 |
( B.25) |
wobei Folgendes gilt:
| W | Landemasse, |
| R | Gleitzahl entsprechend der Klappenstellung bei ausgefahrenem Fahrwerk, |
| γ | Gleitwinkel, kann beim Landeanflug als konstant angenommen werden. Typische Werte fürγ sind:
γ = -3° für strahlgetriebene oder mehrmotorige propellergetriebene Luftfahrzeuge, γ = -5° für einmotorige propellergetriebene Luftfahrzeuge. |
Bei Gegenwind mit anderen Windgeschwindigkeiten als 8 kn berechnet sich der durchschnittliche korrigierte Nettoschub nach
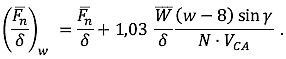 |
( B.26) |
Die zurückgelegte horizontale Entfernung wird berechnet durch:
| Δs = ((h2 - h1) / tanγ ) . | ( B.27) |
Δs ist positiv, weilh1 >h2 undγ negativ ist.
C Modellierung der seitlichen Streuung des Kurses über Grund
Bei fehlenden Radardaten wird die seitliche Streuung des Kurses über Grund ausgehend von der Annahme modelliert, dass die Streuung der senkrecht zur Kernstrecke verlaufenden Unterstrecken einer Gaußschen Normalverteilung folgt.
Abbildung C.1: Unterteilung eines Kurses über Grund in 15 Unterstrecken
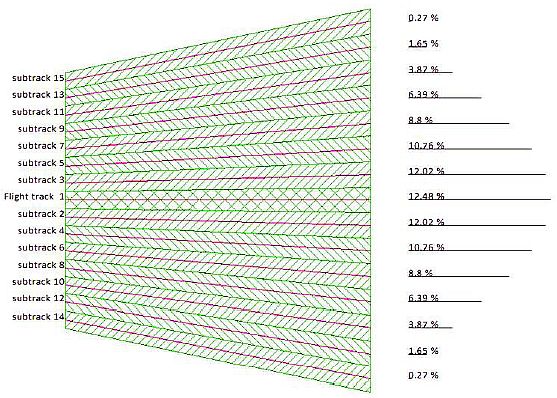
Die Breite des Korridors beträgt das Fünffache der Standardabweichung der Streuung des Kurses über Grund. Die laterale Flugbahnstreuung wird mit fünfzehn Unterstrecken modelliert, die sich in gleichmäßigen Abständen in den Grenzbereichen ±2,5S des in Abbildung C.1 dargestellten Korridors befinden.
D Neuberechnung von NPD-Daten für Nicht-Referenz-Bedingungen
Die Schallpegelanteile der einzelnen Segmente der Flugbahn werden von den NPD-Daten abgeleitet, die in der BUF-D abgelegt sind. Hierbei ist jedoch zu beachten, dass diese Daten mit Hilfe durchschnittlicher atmosphärischer Dämpfungsraten normalisiert wurden.
Da die in Tabelle D.1 angegebenen Dämpfungsraten arithmetische Mittelwerte sind, kann der komplette Satz nicht auf eine einzelne Referenzatmosphäre (d. h. auf keine spezifischen Werte für Temperatur und relative Luftfeuchtigkeit) bezogen werden. Die Dämpfungsraten sind somit nur die Eigenschaften einer rein fiktiven Atmosphäre.
Tabelle D.1: Verwendete durchschnittliche atmosphärische Dämpfungsraten für die Normalisierung von NPD-Daten in der BUF-D
| Mittenfrequenz des Terzbandesfn [Hz] |
Dämpfungsrate an,ref [dB/100m] |
| 50 | 0,033 |
| 63 | 0,033 |
| 80 | 0,033 |
| 100 | 0,066 |
| 125 | 0,066 |
| 160 | 0,098 |
| 200 | 0,131 |
| 250 | 0,131 |
| 315 | 0,197 |
| 400 | 0,230 |
| 500 | 0,295 |
| 630 | 0,361 |
| 800 | 0,459 |
| 1.000 | 0,590 |
| 1.250 | 0,754 |
| 1.600 | 0,983 |
| 2.000 | 1,311 |
| 2.500 | 1,705 |
| 3.150 | 2,295 |
| 4.000 | 3,115 |
| 5.000 | 3,607 |
| 6.300 | 5,246 |
| 8.000 | 7,213 |
| 10.000 | 9,836 |
Bei den Dämpfungsraten in Tabelle D.1 kann davon ausgegangen werden, dass sie hinsichtlich Temperatur und relativer Luftfeuchtigkeit über angemessene Bereiche hinweg gültig sind. Um jedoch den eventuellen Anpassungsbedarf zu prüfen, wurden mittlere Luftabsorptionsbeiwerte für die durchschnittliche FlugplatztemperaturT und die relative LuftfeuchtigkeitRH in Deutschland berechnet. Die Dämpfungsraten für Standardbedingungen in Deutschland sind in Tabelle D.2 aufgeführt. Die Abweichung der Dämpfungsraten für Deutschland von denen in Tabelle D.1 sind hinreichend gering, so dass eine Neuberechnung der NPD-Daten für Nicht-Referenz-Bedingungen nicht erfolgt.
Tabelle D.2: Berechnete Dämpfungsraten bezüglich den meteorologischen Referenzbedingungen in Deutschland (Temperatur 10° Celsius, relative Luftfeuchtigkeit 70 %)
| Mittenfrequenz des Terzbands fn [ Hz] |
Dämpfungsrate αn,866A = (ϑ = 10° C,RH = 70 %) [dB/100m] |
| 50 | 0,021 |
| 63 | 0,027 |
| 80 | 0,034 |
| 100 | 0,043 |
| 125 | 0,053 |
| 160 | 0,068 |
| 200 | 0,086 |
| 250 | 0,107 |
| 315 | 0,135 |
| 400 | 0,172 |
| 500 | 0,216 |
| 630 | 0,273 |
| 800 | 0,349 |
| 1.000 | 0,439 |
| 1.250 | 0,573 |
| 1.600 | 0,788 |
| 2.000 | 1,059 |
| 2.500 | 1,469 |
| 3.150 | 2,093 |
| 4.000 | 3,051 |
| 5.000 | 3,697 |
| 6.300 | 5,259 |
| 8.000 | 7,630 |
| 10.000 | 11,156 |
E Segmentkorrektur ΔF
Dieser Anhang enthält die Ableitung der Segmentkorrektur ΔF und des damit verbundenen Energieanteilsalgorithmus gemäß Abschnitt 21.
E.1 Geometrie
Der Energieanteilsalgorithmus basiert auf der Schallabstrahlung einer 90-Grad-Dipol-schallquelle der vierten Potenz. Die Richtungseigenschaften ähneln den Schallverhältnissen von Strahlflugzeugen zumindest in dem Winkelbereich, der den Schallexpositionspegel unter und seitlich der Flugbahn des Luftfahrzeugs am meisten beeinflusst.
Abbildung E.1: Geometrie zwischen Flugbahn und Immissionsort O
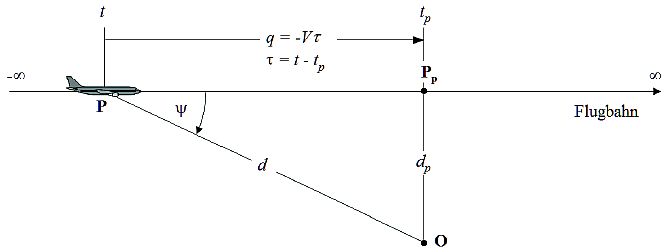
Abbildung E.1 illustriert die Geometrie der Schallausbreitung zwischen der Flugbahn und dem ImmissionsortO. Das Luftfahrzeug inP fliegt in stiller gleichförmiger Luft mit einer konstanten Geschwindigkeit auf einer geraden, horizontalen Flugbahn. Der Punkt des kleinsten Vorbeiflugabstands vom Immissionsort istPp . Die Parameter sind:
| d | Abstand des Immissionsortes zum Luftfahrzeug, |
| dp | senkrechter Abstand zwischen dem Immissionsort und der Flugbahn (Schrägabstand), |
| q | AbstandP zuPp ; q = -Vτ , |
| V | Geschwindigkeit des Luftfahrzeugs, |
| t | Zeit, zu der sich das Luftfahrzeug an PunktP befindet, |
| tp | Zeit, zu der sich das Luftfahrzeug am Punkt des kleinsten VorbeiflugabstandsPp befindet, |
| τ | Flugzeit in Bezug auf Zeitpunkt am PunktPp ; T = t - tp , |
| ψ | Winkel zwischen Flugbahn und Luftfahrzeug-Immissionsort-Vektor. |
Es ist zu beachten, dass die Flugzeitτ in Bezug auf den Punkt des kleinsten Vorbeiflugabstands negativ ist, wenn sich das Luftfahrzeug vor dem Immissionsort befindet und in diesem Fall die relative Entfernungq bis zum Punkt des kleinsten Vorbeiflugabstands positiv wird. Hat das Luftfahrzeug den Immissionsort passiert, wirdq negativ.
E.2 Schätzung des Energieanteils
Das Grundkonzept des Energieanteils besteht darin, die am Immissionsort erzeugte SchallexpositionE durch ein FlugbahnsegmentP1P2 auszudrücken, wobeiP1 der Anfangspunkt undP2 der Endpunkt ist. Hierzu wird die ExpositionE∞ aus der gesamten unendlichen Vorbeiflugbahn mit dem Energieanteils-FaktorF multipliziert:
| E = F · E∞ | ( E.1) |
Die SchallexpositionE kann in Bezug auf das Zeitintegral des mittleren quadratischen (gewichteten) Schalldruckpegels ausgedrückt werden, d. h.
| E = const · ∫p2 (τ) dτ . | ( E.2) |
Daher muss zur Berechnung vonE der mittlere quadratische Schalldruck in Abhängigkeit von den bekannten geometrischen und betrieblichen Parametern ausgedrückt werden. Das bedeutet für eine 90°-Dipolschallquelle:
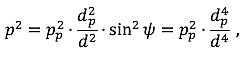 |
( E.3) |
wobeip2 undp2p die mittleren quadratischen Schalldrücke sind, die vom Luftfahrzeug beim Passieren der PunkteP undPp erzeugt werden.
Der Termd2p/d2 in Gleichung ( E.3) beschreibt nur den Mechanismus der bei einer Punktquelle üblichen kugelförmigen Abstrahlung, unendlichen Schallgeschwindigkeit und gleichförmigen, nichtdissipativen Atmosphäre. Alle anderen physikalischen Effekte - Richtcharakteristik der Schallquelle, endliche Schallgeschwindigkeit, Luftabsorption, Doppler-Effekt usw. - werden implizit im Term sin2ψ erfasst. Dieser Term bewirkt die inverse Abnahme des mittleren quadratischen Schalldrucks alsd4 ; daher der Ausdruck Schallquelle "vierter Potenz".
Mit den Substitutionen
| d2 = d2p + q2 = d2p + (Vτ)2 | ( E.4) |
und
 |
( E.5) |
kann der mittlere quadratische Schalldruck in Abhängigkeit von der Zeit ausgedrückt werden, wobei die Schallausbreitungszeit unberücksichtigt bleibt:
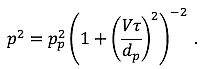 |
( E.6) |
Wird dies in die Gleichung ( E.2) eingesetzt und die Substitution durchgeführt
| α = (Vτ / dp) , | ( E.7) |
kann die Schallexposition am Immissionsort aus dem Vorbeiflug im Zeitintervall [τ1, τ2] ausgedrückt werden als
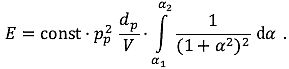 |
( E.8) |
Die Lösung dieses Integrals ist
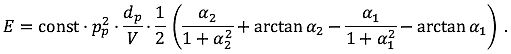 |
( E.9) |
Die Integration über das Intervall [-∞, +∞] (d. h. über die gesamte unendliche Flugbahn) ergibt den folgenden Ausdruck für die Gesamtexposition E∞ :
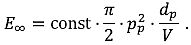 |
( E.10) |
Damit ergibt sich für den Energieanteil nach Gleichung ( E.1):
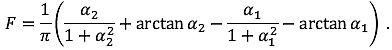 |
( E.11) |
E.3 Widerspruchsfreiheit zwischen den Höchst- und den zeitintegrierten Werten - der skalierte Abstand
Eine Konsequenz aus der Verwendung des einfachen Dipolmodells bei der Bestimmung des Energieanteils ist die implizite Unterstellung einer spezifischen theoretischen Differenz ΔL zwischen MaximalpegelLmax und SchallexpositionspegelLE . Wenn das Fluglärmberechnungsverfahren in sich widerspruchsfrei sein soll, muss diese Differenz gleich der Differenz der aus den NPD-Kurven bestimmten Werte sein. Ein Problem besteht darin, dass die NPD-Daten aus Fluglärmmessungen abgeleitet sind und nicht zwangsläufig mit der einfachen Theorie übereinstimmen. Deshalb muss die Theorie um ein flexibles Element erweitert werden. Da die Variablen α1 und α2 aber grundsätzlich über Geometrie und Fluggeschwindigkeit bestimmt werden, gibt es hier keinen zusätzlichen Freiraum.
Eine Lösung bietet das Konzept einesskalierten Abstandsdλ, das nachfolgend beschrieben wird.
Der Schallexpositionspegel LE,∞ , der in der BUF-D in tabellarischer Form in Abhängigkeit vondp für eine ReferenzgeschwindigkeitVref enthalten ist, kann ausgedrückt werden als
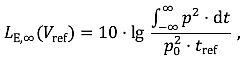 |
( E.12) |
wobei Folgendes gilt:
| po | Standard-Referenzdruck und |
| tref | Referenzzeit für den Schallexpositionspegeltref = 1s . |
Das ergibt für die tatsächliche GeschwindigkeitV
| LE,∞(V) =LE,∞(Vref) + 10 · lg (Vref /V) . | ( E.13) |
Dementsprechend lässt sich der maximale SchalldruckpegelLmax wie folgt ausdrücken:
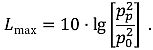 |
( E.14) |
Wird aus den Gleichungen ( E.2) und ( E.10) die Beziehung
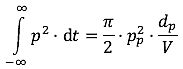 |
( E.15) |
berücksichtigt, lässt sich für die Dipolschallquelle die Differenz ΔL mit Hilfe der Gleichungen ( E.10), ( E.13) und ( E.14) wie folgt darstellen:
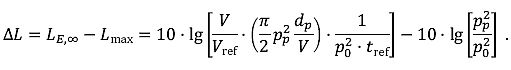 |
( E.16) |
Diese kann nur dann dem aus den NPD-Daten ermittelten Wert von ΔL entsprechen, wenn der zur Berechnung des Energieanteils verwendete Schrägabstanddp durch einenskalierten Abstand dλ ersetzt wird, der gegeben ist durch
| dλ = (2 / π) · Vref · tref ·10(L,E,∞ -Lmax)/10 | ( E.17) |
| oder | |
| dλ = do ·10(L,E,∞ -Lmax)/10 | ( E.18) |
| mit | |
| do = (2 / π) · Vref · tref | ( E.19) |
Bei Ersatz vondp durchdλ in Gleichung ( E.7) und die Verwendung der Definitionq = -Vτ aus Abbildung E.1 lassen sich die Parameter α1 und α2 in Gleichung ( E.11) wie folgt schreiben (indemq = q1 an den Anfangspunkt undq-λ =q2 an den Endpunkt eines Flugbahnlängensegmentsλ gesetzt wird)
| α1 = (-q1 /dλ) | ( E.20) |
| und | |
| α2= ((-q1 + λ) /dl) | ( E.21) |
Da der eigentliche Schrägabstand durch einen skalierten Abstand ersetzt werden muss, vereinfacht sich das 90-Grad-Dipolmodell der vierten Potenz. Andererseits erfährt das Modell durch die Verwendung von messwertbezogenen Daten eine In-Situ-Kalibrierung, so dass der Algorithmus zur Berechnung des Energieanteils als halbempirisch angesehen werden kann.
_____
1) Eigentlich unterhalb des Luftfahrzeugs senkrecht zur Tragflächenachse und Flugrichtung; angenommen als vertikal unterhalb des Luftfahrzeugs bei Nichtkurvenflug (d. h. Nichtschrägflug).
2) Die Zeit wird über die Fluggeschwindigkeit ausgewiesen.
3) Versetzte Landeschwellen können durch die Festlegung zusätzlicher Start-/Landebahnen berücksichtigt werden.
4) Mitunter werden berechnete Pegel bei 4 m oder höher angefragt. Wie ein Vergleich der Messungen in 1,2 m und 10 m Höhe und eine theoretische Berechnung der Bodeneffekte zeigen, sind die Abweichungen des A-bewerteten Schallexpositionspegels relativ unempfindlich gegenüber der Immissionsorthöhe. Die Abweichungen sind im Allgemeinen kleiner als 1 Dezibel, es sei denn, der maximale Schalleinfallswinkel ist kleiner als 10° und das A-bewertete Spektrum am Immissionsort hat sein Maximum im Bereich von 200 bis 500 Hz. Derartige Spektren mit vorwiegend niedrigen Frequenzen können z.B. in großen Entfernungen bei Triebwerken mit niedrigem Nebenstromverhältnis sowie bei Propellermotoren mit diskreten tieffrequenten Tönen auftreten.
5) Flugdatenschreiber speichern ausführliche Betriebsdaten. Diese sind jedoch nicht ohne weiteres zugänglich und in der Beschaffung teuer. Daher ist ihre Verwendung für Lärmmodellierungszwecke in der Regel auf besondere Projekte und Modellentwicklungsstudien beschränkt.
6) In der Regel verlaufen die Achsen der lokalen Koordinaten parallel zur Achse der Karte, auf der die Konturen gezeichnet werden. Zuweilen ist es jedoch sinnvoll, diex-Achse parallel zur Start- und Landebahn zu wählen, um ohne Heranziehung eines feinmaschigen Rechengitters symmetrische Konturen zu erhalten (siehe Abschnitt 28).
7) Bei unebenem Boden kann sich der Immissionsort oberhalb des Luftfahrzeugs befinden. In diesem Fall wirdz* und der entsprechende Höhenwinkelβ gleich null gesetzt.
8) Dazu sollte die Gesamtlänge des Kurses über Grund stets größer sein als die Gesamtlänge des Flugprofils. Dies lässt sich gegebenenfalls erreichen, indem dem letzten Segment des Kurses über Grund gerade Segmente geeigneter Länge hinzugefügt werden.
9) Auf diese einfache Weise definiert, ist die Gesamtlänge der segmentierten Bahn etwas kleiner als die der kreisförmigen Bahn. Der sich daraus ergebende Konturenfehler ist jedoch unerheblich, wenn die Winkelschritte unter 30° liegen.
10) Selbst wenn die Triebwerksleistungseinstellungen entlang eines Segments konstant bleiben, können sich Vortriebskraft und Beschleunigung aufgrund einer Luftdichteänderung mit zu- oder abnehmender Höhe verändern. Für die Zwecke der Lärmmodellierung sind diese Änderungen jedoch in der Regel unerheblich.
11) Der LE mit 10-dB-down-time kann bis zu 0,5 dB niedriger sein als der über eine längere Dauer bewertete LE . Mit Ausnahme von schrägen Abständen, bei denen die Pegel hoch sind, lassen Fremdgeräusche längere Messintervalle als nicht praktikabel erscheinen, und Werte mit 10-dB-down-time sind die Norm. Da Studien zu den Wirkungen von Lärm (zur "Kalibrierung" der Lärmkonturen) sich ebenfalls eher auf Werte mit 10-dB-down-time stützen, gelten die Tabellenangaben der BUF-D als angemessen.
12) Obwohl der Begriff einer unendlich langen Flugbahn für die Definition des Ereignis-SchallexpositionspegelsLpAE eine Rolle spielt, ist er weniger relevant im Falle des Ereignis-MaximalpegelsLpAmax der vom abgestrahlten Lärm des Luftfahrzeugs an einer bestimmten Position oder nahe des kleinsten Vorbeiflugabstands bestimmt wird. Für die Modellierungszwecke wird der NPD-Abstandsparameter als Mindestabstand zwischen dem Immissionsort und dem Segment definiert.
13) Gemäß NPD-Spezifikationen müssen die Daten auf Messungen des stationärenGeradeausflugs, nicht notwendigerweise des waagerechten Flugs, basieren. Zur Schaffung der notwendigen Flugbedingungen kann die Testflugbahn zur Horizontalen geneigt werden. Wie jedoch zu sehen sein wird, führen geneigte Flug bahnen zu Berechnungsproblemen, so dass es bei Verwendung der Daten zur Modellierung sinnvoll ist, die Quellenbahnen als sowohl gerade als auch waagerecht zu visualisieren.
14) Die Korrektur heißtDauerkorrektur, weil sie die Wirkungen derGeschwindigkeit des Luftfahrzeugs auf die Dauer des Schallereignisses berücksichtigt. Dabei wird von der einfachen Annahme ausgegangen, dass bei sonst gleichen Bedingungen die Dauer, und somit die empfangene Schallenergie, umgekehrt proportional zur Quellgeschwindigkeit ist.
15) Je nach Definition des verwendeten Lärmindex können die Zeiträume von diesen dreien abweichen.
16) Abkommen vom 7. Dezember 1944 über die Internationale Zivilluftfahrt (BGBl. 1956 II S. 411)
17) Luftfahrtbehörden legen in der Regel eine untere Schubgrenze fest, oftmals 25 % unter dem Höchstwert.
18) Reduzierte Schubwerte nach Anfangssteigflug mit Startleistung.
19) Es werden Untersegmente eingefügt, um Kontursprünge an den Verbindungsstellen zwischen Geradeaus- und Kurvenflug infolge abrupter Änderungen des Querneigungswinkels zu vermeiden und lineare Querneigungswinkelübergänge über die ersten und letzten 5 Grad der Flugkurve zu ermöglichen. In den Flugleistungsrechnungen ist das nicht notwendig; der Querneigungswinkel ist immer durch Gleichung ( B.8) gegeben.
20) Das Computermodell sollte in beiden Fällen so programmiert werden, dass man über die Diskrepanz informiert wird.
 |
ENDE |  |
(Stand: 20.01.2025)
Alle vollständigen Texte in der aktuellen Fassung im Jahresabonnement
Nutzungsgebühr: 90.- € netto (Grundlizenz)
(derzeit ca. 7200 Titel s.Übersicht - keine Unterteilung in Fachbereiche)
Die Zugangskennung wird kurzfristig übermittelt
? Fragen ?
Abonnentenzugang/Volltextversion
...
X
⍂
↑
↓