Für einen individuellen Ausdruck passen Sie bitte die Für einen individuellen Ausdruck passen Sie bitte dieEinstellungen in der Druckvorschau Ihres Browsers an. ▢ Regelwerk Anhang B |  |
ETAG 001 - Anhang C: Bemessungsverfahren für Verankerungen *
Leitlinie für die Europäische Technische Zulassung
für Metalldübel zur Verankerung im Beton
Ausgabe 1997
Geändert Oktober 2001
2. Änderung November 2006
3. Änderung August 2010
Vom 28. Oktober 2011
(BAnz Nr. 27a S. 70)
Archiv 2008
Einleitung
Die Bemessungsverfahren für Verankerungen dienen der Bemessung von Dübelverankerungen nach dem Sicherheits- und Bemessungskonzept im Rahmen der europäischen technischen Zulassungen (ETA).
Die Bemessungsverfahren im Anhang C beruhen auf der Annahme, dass die erforderlichen Versuche zur Beurteilung der zulässigen Anwendungsbedingungen entsprechend Teil 1 und den nachfolgenden Teilen durchgeführt wurden. Daher ist der Anhang C eine Vorbedingung für die Beurteilung der Dübel. Bei Verwendung anderer Bemessungsverfahren sind die durchzuführenden Versuche erneut zu überprüfen.
Die ETAs für Dübel enthalten nur die charakteristischen Kennwerte der einzelnen zugelassenen Dübel. Die Bemessung der Verankerungen (z.B. Anordnung von Dübeln in einer Dübelgruppe, Einfluss von Bauteilrändern oder -ecken auf die charakteristische Tragfähigkeit) muss nach den in den Kapiteln 3 bis 5 beschriebenen Bemessungsverfahren unter Berücksichtigung der entsprechenden charakteristischen Dübelkennwerte erfolgen.
Kapitel 7 enthält zusätzliche Nachweise zur Sicherung der charakteristischen Bauteiltragfähigkeit, die für alle Dübelsysteme gleichermaßen zutreffen.
Die Bemessungsverfahren gelten für alle Dübelarten. Jedoch sind die nachstehend aufgeführten Gleichungen nur für Dübel zu verwenden, die den vorliegenden Erfahrungen entsprechen (siehe Anhang B). Sind die Werte für charakteristische Tragfähigkeit, Achsabstände, Randabstände zwischen Bemessungsverfahren und ETA unterschiedlich, so gelten die in der ETA angegebenen Werte. Bei Fehlen nationaler Vorschriften können die nachstehend aufgeführten Teilsicherheitsbeiwerte verwendet werden.
1 Geltungsbereich
1.1 Dübelarten, Dübelgruppen und Dübelanzahl
Die Bemessungsverfahren gelten für die Bemessung von Verankerungen in Beton mit zugelassenen Dübeln, die die Anforderungen dieser Leitlinie erfüllen. Die charakteristischen Dübelkennwerte sind in der jeweiligen ETA aufgeführt.
Die Bemessungsverfahren gelten für Einzeldübel und Dübelgruppen. Bei einer Dübelgruppe werden die Lasten über ein steifes Anbauteil in die einzelnen Dübel der Gruppe übertragen. In einer Dübelgruppe sind nur Dübel gleicher Art, Größe und Länge zu verwenden.
Die Bemessungsverfahren umfassen Einzeldübel und Dübelgruppen nach Bild 1.1 und 1.2. Andere Dübelanordnungen, z.B. in dreieckiger oder runder Form, sind ebenfalls zulässig; jedoch sollten die Vorschriften dieses Bemessungsverfahrens auf der Grundlage von ingenieurmäßiger Planung angewendet werden.
Diese Bemessung gilt grundsätzlich nur, wenn der Durchmesser df des Durchgangslochs im Anbauteil nicht größer als der Wert nach Tabelle 4.1 ist.
Ausnahmen:
- Für zugbelastete Verankerungen ist ein größerer Durchmesser des Durchgangslochs nur akzeptabel, wenn eine entsprechende Unterlegscheibe verwendet wird.
- Für Verankerungen, die Querbeanspruchung oder kombinierter Zug- und Querbeanspruchung ausgesetzt sind, wenn der Spalt zwischen dem Loch und dem Anbauteil mit Mörtel ausreichender Druckfestigkeit verfüllt oder mit anderen geeigneten Mitteln beseitigt wird.
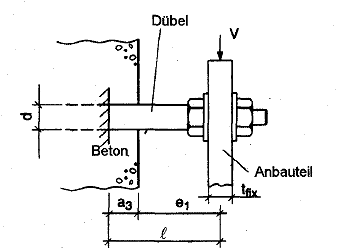
Bild 1.1 Verankerungen, die durch die Bemessungsverfahren abgedeckt sind
- alle Lastrichtungen, wenn sich Dübel randfern befinden (c > max (10 hef, 60d))
- nur Zugbelastung, wenn sich Dübel randnah befinden (c < max (10 hef, 60d))
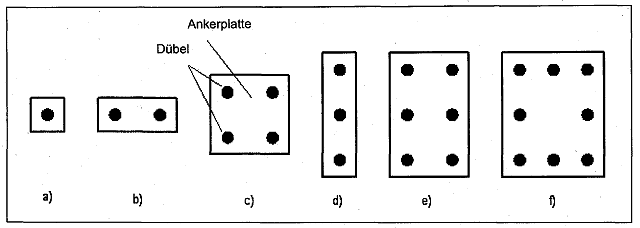
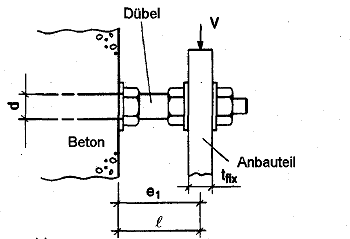
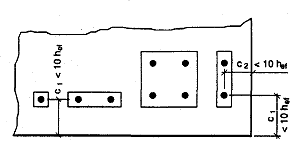
Bild 1.2 Verankerungen, die durch die Bemessungsverfahren abgedeckt sind
Querbeanspruchung, wenn sich Dübel randnah befinden (c < max (10 hef, 60d))
1.2 Betonbauteile
Das Betonbauteil muss aus Normalbeton mindestens der Festigkeitsklasse C20/25 und höchstens C50/60 nach EN 206 [8] bestehen und darf nur durch vorwiegend ruhende Lasten beansprucht werden. Der Beton darf gerissen oder ungerissen sein. Im Regelfall ist aus Gründen der Einfachheit von gerissenem Beton auszugehen; andernfalls ist nachzuweisen, dass der Beton ungerissen ist (siehe 4.1).
1.3 Lastarten und -richtungen
Die Bemessungsverfahren gelten für Dübel unter vorwiegend ruhender Belastung. Sie gelten nicht für Dübel, die Druckbeanspruchungen oder Stoß- oder Erdbebenlasten unterliegen.
1.4 Sicherheitsklassen
Verankerungen, die diesen Bemessungsverfahren entsprechen, berücksichtigen Verankerungen, bei deren Versagen eine Gefahr für Leben oder Gesundheit von Menschen und/oder erhebliche wirtschaftliche Folgen bestehen.
2 Begriffe und Formelzeichen
Die in den Bemessungsverfahren häufig verwendeten Formelzeichen sind nachfolgend erläutert. Weitere Begriffe sind im Text erklärt.
2.1 Indizes
S = Einwirkung
R = Widerstand
M = Werkstoff
k = charakteristischer Wert
d = Bemessungswert
s = Stahl
c = Beton
cp = Betonausbruch auf der lastabgewandten Seite
p = Herausziehen
sp = Spalten
u = Höchstwert
y = Streckgrenze
2.2 Einwirkungen und Widerstände
F = Kraft im Allgemeinen (resultierende Kraft)
N = Normalkraft (positiv: Zugkraft; negativ: Druckkraft)
V = Querkraft
M = Moment
| Fsk (NSk; VS; MSk; MT,Sk) | = | charakteristischer Wert der auf einen Einzeldübel oder auf die Ankerplatte einer Dübelgruppe einwirkenden Kraft (Normalkraft, Querkraft, Biegemoment, Torsionsmoment) |
| Fsd (NSd; VSd; MSd MT,sd) | = | Bemessungswert der Einwirkung |
| Nhsd (Vh Sd) | = | Bemessungswert der einwirkenden Zugkraft (Querkraft) für den höchstbeanspruchten Dübel einer Dübelgruppe, berechnet nach 4.2 |
| Ngsd (Vg Sd) | = | Bemessungswert der Summe (resultierenden) der einwirkenden Zug(Quer-)Lasten auf die zugbeanspruchten (querbeanspruchten) Dübel einer Gruppe, berechnet nach 4.2 |
| FRk (NRk; VRk) | = | charakteristischer Wert des Widerstandes eines Einzeldübels bzw. einer Dübelgruppe (Normalkraft, Querkraft) |
| FRd (NRd; VRd) | = | Bemessungswert des Widerstandes |
2.3 Beton und Stahl
| fck,cube | = | charakteristische Druckfestigkeit des Betons, gemessen an Würfeln von 150 mm Seitenlänge (Wert der Betonfestigkeitsklasse nach EN 206 [8]) |
| fyk | = | charakteristische Streckgrenze des Stahls (Nennwert) |
| fuk | = | charakteristische Zugfestigkeit des Stahls (Nennwert) |
| As | = | Spannungsquerschnitt des Stahls |
| Wel | = | elastisches Widerstandsmoment, ermittelt aus dem Spannungsquerschnitt des Stahls (πd3/32 für einen Rundquerschnitt mit Durchmesser d) |
2.4 Charakteristische Dübelkennwerte (siehe Bild 2.1)
| a | = | Abstand zwischen den äußeren Dübeln benachbarter Dübelgruppen oder zu Einzeldübeln |
| a1 | = | Abstand zwischen den äußeren Dübeln benachbarter Dübelgruppen oder zu Einzeldübeln in Richtung 1 |
| a2 | = | Abstand zwischen den äußeren Dübeln benachbarter Dübelgruppen oder zu Einzeldübeln in Richtung 2 |
| b | = | Breite des Betonbauteils |
| c | = | Randabstand |
| c1 | = | Randabstand in Richtung 1; bei randnahen Verankerungen mit Querbeanspruchung ist c1 der Randabstand in Richtung der Last (siehe Bild 2.1b und Bild 5.7) |
| c2 | = | Randabstand in Richtung 2; Richtung 2 ist senkrecht zu Richtung 1 |
| ccr | = | Randabstand zur Gewährleistung der Übertragung des charakteristischen Widerstandes (Bemessungsverfahren B und C) |
| ccr,N | = | Randabstand zur Gewährleistung der Übertragung des charakteristischen Zugwiderstandes eines Einzeldübels ohne Einfluss von Achs- und Randabstand bei Versagen durch Betonausbruch (Bemessungsverfahren A) |
| ccr,sp | = | Randabstand zur Gewährleistung der Übertragung des charakteristischen Zugwiderstandes eines Einzeldübels ohne Einfluss von Achs- und Randabstand bei Versagen durch Spalten des Betons (Bemessungsverfahren A) |
| cmin | = | minimaler zulässiger Randabstand |
| d | = | Durchmesser des Dübelbolzens oder Gewindedurchmesser |
| dnom | = | Außendurchmesser des Dübels |
| d0 | = | Bohrernenndurchmesser |
| h | = | Dicke des Betonbauteils |
| hef | = | effektive Verankerungstiefe |
| hmin | = | Mindestbauteildicke |
| lf | = | wirksame Dübellänge bei Querlast. Für Bolzen mit einem gleichmäßigen Querschnitt über die Dübellänge ist der Wert hof für die wirksame Dübellänge zu verwenden. Für Dübel mit verschiedenen Hülsen und verengten Querschnitten darf die wirksame Länge nur von der Betonoberfläche bis zur relevanten Hülse angesetzt werden. |
| s | = | Achsabstand innerhalb einer Dübelgruppe |
| s1 | = | Achsabstand innerhalb einer Dübelgruppe in Richtung 1 |
| s2 | = | Achsabstand innerhalb einer Dübelgruppe in Richtung 2 |
| scr | = | Achsabstand zur Gewährleistung der Übertragung des charakteristischen Widerstandes (Bemessungsverfahren B und C) |
| scr, N | = | Achsabstand zur Gewährleistung der Übertragung des charakteristischen Zugwiderstandes eines Einzeldübels ohne Einfluss von Achs- und Randabstand bei Versagen durch Betonausbruch (Bemessungsverfahren A) |
| scr,sp | = | Achsabstand zur Gewährleistung der Übertragung des charakteristischen Zugwiderstandes eines Einzeldübels ohne Einfluss von Achs- und Randabstand bei Versagen durch Spalten des Betons (Bemessungsverfahren A) |
| smin | = | minimaler zulässiger Achsabstand |
Bild 2.1 Betonbauteil, Dübelachs- und -randabstände
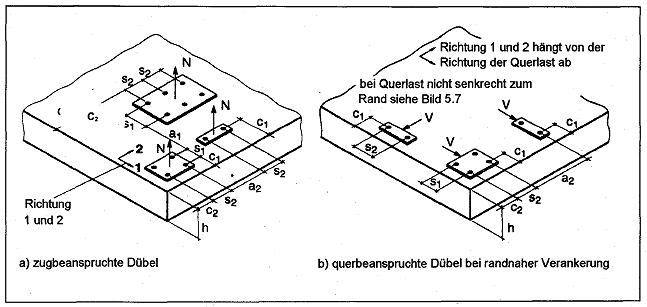
3 Bemessungs- und Sicherheitskonzept
3.1 Allgemeines
Bei der Bemessung von Dübelverankerungen sind die allgemeinen Regeln in EN 1990 anzuwenden. Es ist nachzuweisen, dass der Bemessungswert der Einwirkung Sd den Bemessungswert der Widerstände Rd nicht überschreitet.
Sd < Rd (3.1)
Sd = Bemessungswert der Einwirkungen
Rd = Bemessungswert der Widerstände
Die für die Bemessung heranzuziehenden Einwirkungen sind einem veröffentlichten nationalen Anhang zu EN 1991 zu entnehmen. Gibt es diesen nicht, ist auf nationale Vorschriften oder, wenn diese ebenfalls fehlen, auf EN 1991 zurückzugreifen.
Die Teilsicherheitsbeiwerte für Einwirkungen sind einem veröffentlichten nationalen Anhang zu EN 1991 zu entnehmen. Gibt es diesen nicht, ist auf nationale Vorschriften oder, wenn diese ebenfalls fehlen, auf EN 1991 zurückzugreifen.
Der Bemessungswert des Widerstandes wird wie folgt berechnet:
Rd = Rk/γM (3.2)
Rk = charakteristischer Widerstand eines Einzeldübels oder einer Dübelgruppe
γM = Teilsicherheitsbeiwert für den Materialwiderstand
3.2 Grenzzustand der Tragfähigkeit
3.2.1 Bemessungswert des Widerstandes
Der Bemessungswert des Widerstandes ist nach Gleichung (3.3) zu ermitteln. Beim Bemessungsverfahren A wird der charakteristische Widerstand für alle Lastrichtungen und Versagensarten berechnet.
Bei den Bemessungsverfahren B und C wird nur ein charakteristischer Widerstand für alle Lastrichtungen und Versagensarten angegeben.
3.2.2 Teilsicherheitsbeiwerte für Widerstände
Bei Fehlen nationaler Vorschriften können die folgenden Teilsicherheitsbeiwerte verwendet werden. Jedoch darf der Wert γ2 nicht geändert werden, da er die Charakteristik des Dübels beschreibt.
3.2.2.1 Betonversagen, Versagen durch Spalten und Herausziehen
Die Teilsicherheitsbeiwerte für Betonversagen (γMc), Spalten (γMsp) und Herausziehen (γMp) sind in der jeweiligen ETA angegeben.
Für Dübel, die den vorliegenden Erfahrungen entsprechen, ermittelt sich der Teilsicherheitsbeiwert γmc aus:γ Mc = γc γ2
γc = Teilsicherheitsbeiwert für Beton auf Druck = 1,5
γ2 = Teilsicherheitsbeiwert zur Berücksichtigung der Montagesicherheit eines Dübelsystems
Der Teilsicherheitsbeiwert γ2 wird ermittelt aus den Ergebnissen der Montagesicherheitsversuche; siehe Teil 1, 6.1.2.2.2.
Zuglast
γ2 = 1,0 für Systeme mit hoher Montagesicherheit = 1,2 für Systeme mit normaler Montagesicherheit = 1,4 für Systeme mit geringer, aber noch ausreichender Montagesicherheit Querlast (Betonausbruch auf der lastabgewandten Seite, Betonkantenbruch)
γ2 = 1,0
Für die Teilsicherheitsbeiwerte γMsp und γMp darf der Wert für γMc angesetzt werden.
3.2.2.2 Stahlversagen
Die Teilsicherheitsbeiwerte γMs für Stahlversagen sind in der jeweiligen ETA angegeben.
Für Dübel, die den vorliegenden Erfahrungen entsprechen, ermitteln sich die Teilsicherheitsbeiwerte γMs in Abhängigkeit von der Beanspruchungsart wie folgt:Zuglast:
γMs = (1,2 / (fyk / fuk) > 1,4 (3.3a)
Querlast mit oder ohne Hebelarm:
γMs = 1,0 / (fyk / fuk) > 1,25 fuk < 800 N/mm2 (3.3b) und fyk/fuk < 0,8 γ Ms = 1,5 fuk > 800 N/mm2 (3.3c) oder fyk/fuk > 0,8
3.3 Grenzzustand der Gebrauchstauglichkeit
Für den Grenzzustand der Gebrauchstauglichkeit muss nachgewiesen werden, dass die bei den charakteristischen Einwirkungen auftretenden Verschiebungen nicht größer sind als die zulässigen Verschiebungen. Zu den charakteristischen Verschiebungen siehe 6. Die zulässige Verschiebung hängt von der jeweiligen Anwendung ab und ist vom zuständigen Planungsingenieur zu beurteilen.
Bei diesem Nachweis dürfen die Teilsicherheitsbeiwerte der Einwirkungen und Widerstände zu 1,0 angenommen werden.
4 Statische Nachweise
4.1 Ungerissener und gerissener Beton
Wenn die Bedingungen in Gleichung (4.1) nicht erfüllt oder nicht geprüft sind, muss gerissener Beton angenommen werden.
In Sonderfällen darf von ungerissenem Beton ausgegangen werden, wenn in jedem Einzelfall nachgewiesen wird, dass im Gebrauchszustand die Dübel mit ihrer gesamten Verankerungstiefe im ungerissenen Beton liegen. Wenn andere Angaben fehlen, dürfen folgende Bedingungen verwendet werden.
Bei Verankerungen mit einer resultierenden Belastung von Fsk
< 60 kN kann von ungerissenem Beton ausgegangen werden, wenn Gleichung (4.1) erfüllt ist:
|
σL + σR < 0 (4.1) | ||
| σL | = | Spannungen im Beton, die durch äußere Lasten einschließlich der Dübellasten hervorgerufen werden |
| σR | = | Spannungen im Beton, die durch innere Zwangsverformungen (z.B. Schwinden des Betons) oder durch von außen wirkende Zwangsverformungen (z.B. durch Auflagerverschiebungen oder Temperaturschwankungen) hervorgerufen werden. Wird kein genauerer Nachweis geführt, sollte σR nach EC 2 [1] zu 3 N/mm2 angenommen werden. |
Die Spannungen σL und σR sind unter der Annahme zu berechnen, dass der Beton ungerissen ist (Zustand I). Bei flächigen Bauteilen, die in zwei Richtungen Lasten abtragen (z.B. Platten, Wände) ist Gleichung (4.1) für beide Richtungen zu erfüllen.
4.2 Lasteinwirkungen auf den Dübel
Beim statischen Nachweis werden die an der Ankerplatte angreifenden Kräfte und Momente angegeben. Für die Bemessung der Verankerung müssen die auf jeden Dübel einwirkenden Lasten unter Berücksichtigung der Teilsicherheitsbeiwerte der Einwirkungen nach 3.1 im Grenzzustand der Tragfähigkeit und nach 3.3 im Grenzzustand der Gebrauchstauglichkeit berechnet werden.
Bei Einzeldübeln sind die auf den Dübel und die auf die Ankerplatte wirkenden Lasten normalerweise gleich. Bei Dübelgruppen müssen die auf die Ankerplatte einwirkenden Lasten, Biege- und Torsionsmomente auf die auf den einzelnen Dübel der Gruppe wirkenden Zug- und Querkräfte verteilt werden. Diese Verteilung ist nach der Elastizitätstheorie zu berechnen.
4.2.1 Zuglasten
Im Allgemeinen sind die aufgrund der an der Ankerplatte angreifenden Lasten und Biegemomente auf jeden Dübel einwirkenden Zuglasten nach der Elastizitätstheorie nach folgenden Annahmen zu berechnen:
- Die Ankerplatte darf sich unter den einwirkenden Schnittkräften nicht verformen. Um diese Voraussetzung zu gewährleisten, muss die Ankerplatte ausreichend steif sein.
- Die Steifigkeit aller Dübel ist gleich und entspricht dem Elastizitätsmodul des Stahls. Das Elastizitätsmodul des Betons ist in [1] angegeben. Vereinfachend darf Ec = 30.000 N/mm2 angesetzt werden.
- In der druckbeanspruchten Zone unter der Ankerplatte tragen die Dübel nicht zur Aufnahme der Normalkräfte bei (siehe Bild 4.1b).
In bestimmten Fällen, bei denen die Ankerplatte nicht ausreichend steif ist, muss die Elastizität der Ankerplatte bei der Berechnung der einwirkenden Lasten auf den Dübel berücksichtigt werden.
Bei Dübelgruppen mit auf die einzelnen Dübel einer Gruppe einwirkenden unterschiedlichen Zugkräften Ns, darf die Exzentrizität eN der Zugkraft Ngs der Gruppe berechnet werden (siehe Bild 4.1), um eine genauere Beurteilung des Widerstandes der Dübelgruppe zu ermöglichen,
Bild 4.1 Beispiel für Verankerungen, die einer exzentrischen Zuglast Ngs sausgesetzt sind
a) Exzentrizität in einer Richtung, alle Dübel werden durch eine Zugkraft beansprucht
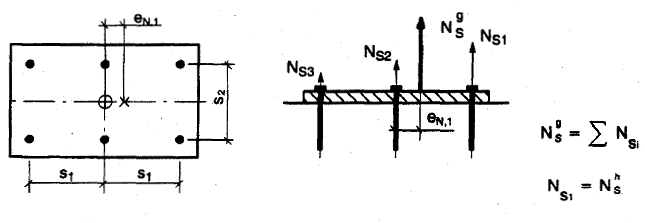
b) Exzentrizität in einer Richtung, nur ein Teil der Dübel wird durch eine Zugkraft beansprucht
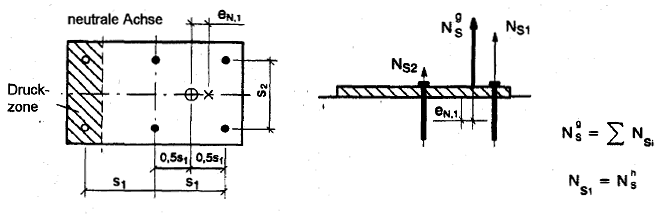
c) Exzentrizität in zwei Richtungen, nur ein Teil der Dübel der Gruppe wird durch eine Zugkraft beansprucht
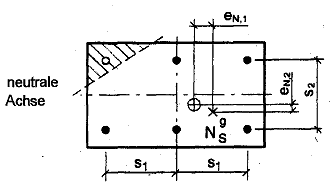
 | zugbeanspruchte Dübel |
 | Schwerpunkt der zugbeanspruchten Dübel |
 | Punkt der resultierenden Zugkraft von zugbeanspruchten Dübel |
Wenn die zugbeanspruchten Dübel einer Gruppe keine rechteckige Form bilden, darf diese Gruppe vereinfachend zu einer rechteckigen Form ergänzt werden (d.h. der Schwerpunkt der zugbeanspruchten Dübel darf in der Mitte der Achse in Bild 4.1c liegend angenommen werden).
4.2.2 Querlasten
4.2.2.1 Verteilung der Querlasten
Die Verteilung der Querlasten hängt von der Versagensart ab:
- Stahlversagen und Betonausbruch auf der lastabgewandten Seite
Alle Dübel nehmen Querlasten auf, wenn der Durchmesser df des Durchgangslochs im Anbauteil nicht größer als der in Tabelle 4.1 angegebene Wert ist (siehe Bilder 4.2 und 4.6).
- Versagen der Betonkante
Nur die ungünstigsten Dübel nehmen Querlasten auf, wenn die Querkraft senkrecht zum Rand wirkt (siehe Bilder 4.3 und 4.7). Querlasten, die parallel zum Rand wirken, werden von allen Dübeln aufgenommen.
Langlöcher in Richtung Querlast verhindern, dass Dübel Querlasten aufnehmen können. Dies kann bei Verankerungen nahe am Bauteilrand günstig sein (siehe Bild 4.4).
Wenn der Durchmesser df des Durchgangslochs größer als der in Tabelle 4.1 angegebene Wert ist, gilt das Bemessungsverfahren nur, wenn der Spalt zwischen Schraube und Anbauteil mit Mörtel ausreichender Druckfestigkeit verfüllt oder mit anderen geeigneten Mitteln beseitigt wird.
Bild 4.2 Beispiele für die Verteilung der Last, wenn alle Dübel Querlasten aufnehmen
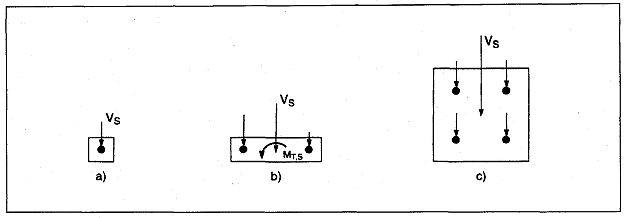
Bild 4.3 Beispiele für die Verteilung der Last, wenn nur die ungünstigsten Dübel Querlasten aufnehmen
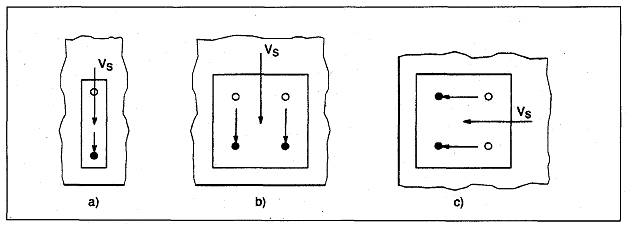
Bild 4.4 Beispiele für die Verteilung der Last bei einer Verankerung mit Langlöchern
Tabelle 4.1 Durchmesser des Durchgangslochs im Anbauteil
| Außendurchmesser d 1) oder dnom 2) (mm) | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 27 | 30 |
| Durchmesser df des Durchgangslochs im Anbauteil (mm) | 7 | 9 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 30 | 33 |
| 1) wenn die Schraube am Anbauteil anliegt 2) wenn die Dübelhülse am Anbauteil anliegt | ||||||||||||
Bei Dübelgruppen mit auf die einzelnen Dübel einer Gruppe einwirkenden unterschiedlichen Querlasten Vsi darf die Exzentrizität ev der Querkraft Vgs der Gruppe berechnet werden (siehe Bild 4.5), um eine genauere Beurteilung der Tragfähigkeit der Dübelgruppe zu ermöglichen.
Bild 4.5 Beispiel für eine Verankerung unter exzentrischer Querlast
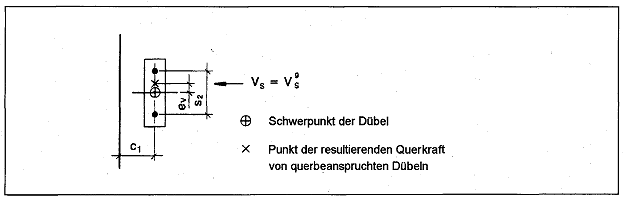
4.2.2.2 Ermittlung der Querlasten
Die Ermittlung der Querlasten auf die Verankerungen in einer Gruppe resultierend aus Querkräften und Torsionsmomenten, die auf ein Anbauteil wirken, wird unter Annahme einer gleichen Steifigkeit aller Verankerungen einer Gruppe nach der Elastizitätstheorie berechnet. Es muss eine gleichmäßige Verteilung gegeben sein. Beispiele sind in Bild 4.6 und 4.7 dargestellt.
Bild 4.6 Ermittlung von Querlasten, wenn alle Dübel Lasten aufnehmen (Stahlversagen und Betonausbruch)
a) Gruppe von drei Dübeln unter Querlast
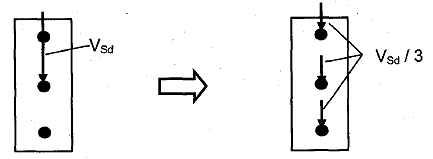
b) Gruppe von vier Dübeln unter Querlast
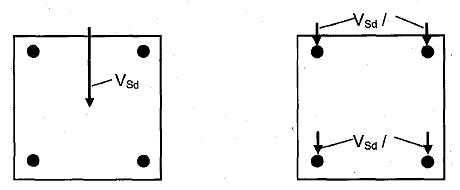
c) Gruppe von vier Dübeln unter schräg einwirkender Querlast
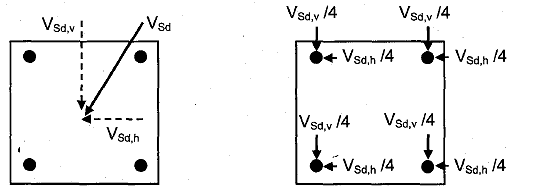
d) Gruppe von vier Dübeln unter Torsionsmoment
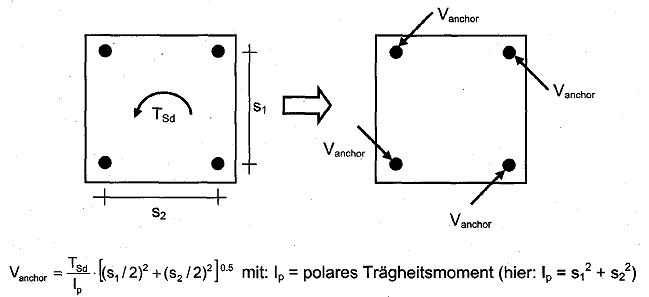
Bild 4.7 Ermittlung von Querlasten, wenn nur die ungünstigsten Dübel Lasten aufnehmen (Betonkantenbruch)
a) Gruppe von zwei Dübeln, die parallel zum Rand belastet werden
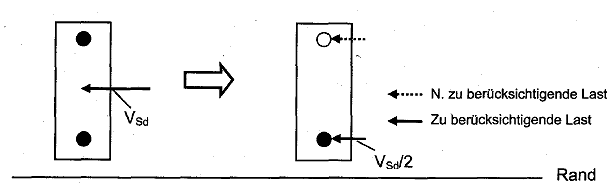
b) Gruppe von vier Dübeln, die durch eine schräg einwirkende Querlast belastet werden
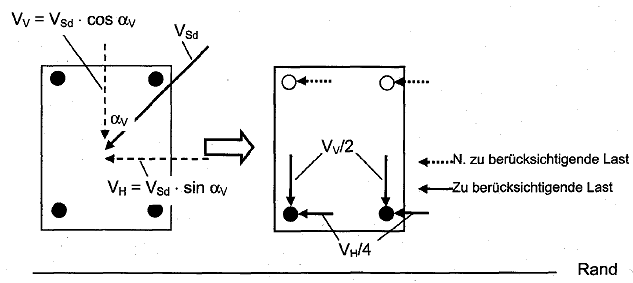
Bei Betonkantenbruch, bei dem nur die ungünstigsten Dübel Last aufnehmen, werden die Komponenten der Last, die senkrecht zum Rand wirken, von den ungünstigsten (randnahen) Dübeln aufgenommen, während die Komponenten der Last, die parallel zum Rand wirkt, aus Gleichgewichtsgründen gleichmäßig auf alle Dübel der Gruppe verteilt wird.
4.2.2.3 Querlasten ohne Hebelarm
Querlasten dürfen/ als ohne Hebelarm auf die Dübel einwirkend angenommen werden, wenn beide der nachfolgenden Bedingungen erfüllt sind:
- Das anzuschließende Bauteil muss aus Metall bestehen und ohne Zwischenlage bzw. mit einer Mörtelausgleichsschicht (Druckfestigkeit > 30 N/mm2) mit einer Stärke < d/2 im Bereich der Verankerung gegen den Beton verspannt sein.
- Das Anbauteil muss auf seiner ganzen Dicke am Dübel anliegen.
4.2.2.4 Querlasten mit Hebelarm
Sind die Bedingungen a) und b) von 4.2.2.3 nicht erfüllt, ist der Hebelarm nach Gleichung (4.2) (siehe Bild 4.8) zu berechnen.
l = a3 + e1 (4.2)
wobei gilt:e1 = Abstand zwischen Querlast und Betonoberfläche
a3 = 0,5 d
a3 = 0, wenn eine Unterlegscheibe und eine Mutter direkt gegen die Betonoberfläche geklemmt sind (siehe Bild 4.8b)
d = Nenndurchmesser der Dübelschraube oder Gewindedurchmesser (siehe Bild 4.8a)
Bild 4.8 Definition des Hebelarms
| a)
| b)
|
Das auf den Dübel wirkende Moment ist nach Gleichung (4.3) zu berechnen.
Msd = Vsd * (l/α M) (4.3)
Der Wert αM hängt vom Einspanngrad des Dübels auf der Anbauteilseite bei der jeweiligen Anwendung ab und ist ingenieurmäßig zu beurteilen.
Von keiner Einspannung (αM = 1,0) ist auszugehen, wenn das Anbauteil sich frei drehen kann (siehe Bild 4.9a). Diese Annahme liegt immer auf der sicheren Seite.
Von voller Einspannung (αM = 2,0) darf nur ausgegangen werden, wenn sich das Anbauteil nicht drehen kann (siehe Bild 4.9b) und das Durchgangsloch im Anbauteil kleiner ist als die in Tabelle 4.1 angegebenen Werte oder der Dübel mit Mutter und Unterlegscheibe gegen das Anbauteil festgeklemmt ist (siehe Bild 4.8). Wird von einer Einspannung des Dübels ausgegangen, muss das Anbauteil in der Lage sein, das Einspannmoment aufzunehmen.
Bild 4.9 Anbauteil ohne (a) und mit (b) Einspannung

5 Grenzzustand der Tragfähigkeit
5.1 Allgemeines
Für die Bemessung von Dübelverankerungen im Grenzzustand der Tragfähigkeit stehen drei Bemessungsverfahren zur Verfügung. Die Bemessungsverfahren und die zugehörigen erforderlichen Versuche zur Ermittlung der zulässigen Anwendungsbedingungen sind in Tabelle 5.1 angegeben. Im Abschnitt 5.2 wird das allgemeine Bemessungsverfahren A beschrieben; in 5.3 und 5.4 werden die vereinfachten Verfahren B und C behandelt. Das zu verwendende Bemessungsverfahren ist in der jeweiligen ETA angegeben.
Entsprechend Gleichung (3.1) muss nachgewiesen werden, dass der Bemessungswert der Einwirkung gleich oder kleiner als der Bemessungswert des Widerstandes ist. Die charakteristischen Dübelkennwerte für die Berechnung des Widerstandes im Grenzzustand der Tragfähigkeit sind in der jeweiligen ETA angegeben.
Der minimale Achs- und Randabstand sowie die Mindestbauteildicke dürfen nicht unterschritten werden.
Der Achsabstand zwischen dem äußeren Dübel benachbarter Dübelgruppen oder der Abstand zu Einzeldübeln muss a > scr,N (Bemessungsverfahren A) bzw. scr (Bemessungsverfahren B und C) betragen.
Tabelle 5.1 Bemessungsverfahren und zugehörige erforderliche Versuche zur Ermittlung der zulässigen Anwendungsbedingungen
| Bemessungsverfahren | gerissener und ungerissener Beton | nur ungerissener Beton | charakteristischer Widerstand für | Versuche nach Anhang B Option | |
| nur C20/25 | C20/25 bis C50/60 | ||||
| A | x | x | 1 | ||
| x | x | 2 | |||
| x | x | 7 | |||
| x | x | 8 | |||
| B | x | x | 3 | ||
| x | x | 4 | |||
| x | x | 9 | |||
| x | x | 10 | |||
| C | x | x | 5 | ||
| x | x | 6 | |||
| x | x | 11 | |||
| x | x | 12 | |||
5.2.1 Allgemeines
Beim Bemessungsverfahren A muss nachgewiesen werden, dass Gleichung (3.1) für alle Lastrichtungen (Zug-, Querbeanspruchung) und alle Versagensarten (Stahlversagen, Herausziehen und Betonversagen) eingehalten ist.
Liegt eine kombinierte Zug- und Querbeanspruchung (Schrägzugbeanspruchung) vor, ist die Interaktionsbedingung nach 5.2.4 einzuhalten.
Bei den Optionen 2 und 8 (siehe Teil 1, Tabelle 5.3) ist fck,cube = 25 N/mm2 in die Gleichungen (5.2a) und (5.7a) einzusetzen.
5.2.2 Widerstand bei Zugbeanspruchung
5.2.2.1 Erforderliche Nachweise
| Einzeldübel | Dübelgruppe | ||
| Stahlversagen | NSd < NRk,s / γMs | Nh Sd < NRk,s / γMs | |
| Herausziehen | NSd < NRk,p / γMp | Nh Sd < NRk,p / γMp | |
| Betonausbruch | NSd < NRk,c /γMc | Ng Sd < NRk,c / γMc | |
| Spalten | NSd < NRk,sp / γMsp | Ng Sd < NRk,p / γMp | |
5.2.2.2 Stahlversagen
Der charakteristische Widerstand N Rk,s eines Dübels bei Stahlversagen ist in der jeweiligen ETA angegeben.
Der Wert N Rk,s ergibt sich aus Gleichung (5.1).
NRk,s = As fuk [N] (5.1)
5.2.2.3 Versagen durch Herausziehen
Der charakteristische Widerstand NRk,p eines Dübels bei Versagen durch Herausziehen ist der jeweiligen ETA zu entnehmen.
5.2.2.4 Betonausbruch
Der charakteristische Widerstand eines Dübels oder einer Dübelgruppe bei Betonausbruch beträgt:
N Rk,c = N= o Rk,c * (Ac,N / Aoc,N) * Ws,N * Wer,N * Wec,N [N] (5.2)
Nachstehend werden die einzelnen Faktoren der Gleichung (5.2) für Dübel angegeben, für die entsprechende Erfahrungen vorliegen:
a) Der Ausgangswert des charakteristischen Widerstandes eines Dübels im gerissenen oder ungerissenen Beton beträgt:
No Rk,c = k1 * √fck,cube * hef 1,5 [N] (5.2a)
fck,cube [N/mm2]; hef [mm]
k1 = 7,2 für Anwendungen im gerissenen Beton
k1 = 10,1 für Anwendungen im ungerissenen Beton
b) Der geometrische Einfluss von Achs- und Randabständen auf den charakteristischen Widerstand wird durch den Verhältniswert Ac,N/Aoc,N berücksichtigt, wobei gilt:
| Aoc,N | = Fläche des Ausbruchkörpers eines Einzeldübels mit großem Achs- und Randabstand auf der Betonoberfläche. Dabei wird der Ausbruchkörper als Pyramide mit der Höhe hef und der Länge der Basisseiten Scr,N idealisiert (siehe Bild 5.1). |
| = Scr,N * Scr,N (5.2b) | |
| Ac,N | = vorhandene Fläche des Ausbruchkörpers der Verankerung auf der Betonoberfläche.
Sie wird begrenzt durch die Überschneidungen der einzelnen Ausbruchkörper benachbarter Verankerungen (s < scr,N) sowie durch Bauteilränder (c < ccr,N). Beispiele für die Berechnung von Ac,N siehe Bild 5.2. |
Die Werte Scr,N und ccr,N sind in der jeweiligen ETA aufgeführt.
Für einen Dübel, der den vorliegenden Erfahrungen entspricht, ist scr,N = 2 Ccr,N = 3 hef anzunehmen.
Bild 5.1 Idealisierter Betonausbruchkörper und Fläche Aoc,N des Ausbruchkörpers eines Einzeldübels
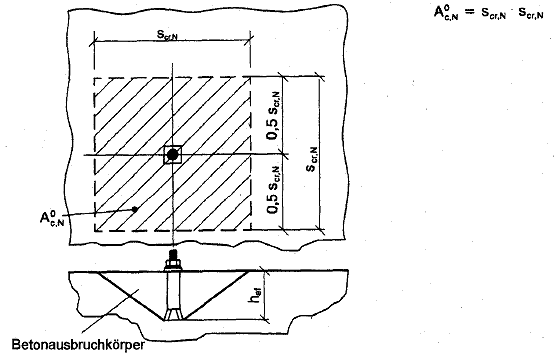
Bild 5.2 Beispiele für vorhandene Flächen Ac,N der idealisierten Betonausbruchkörper bei verschiedenen Dübelanordnungen unter Zugbeanspruchung
a) Einzeldübel am Bauteilrand
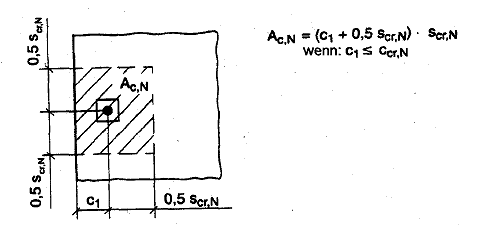
b) Dübelgruppe mit zwei Dübeln am Bauteilrand
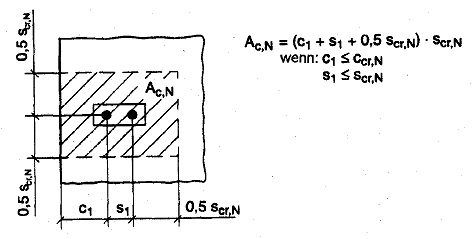
c) Dübelgrupp mit vier Dübeln an der Bauteilecke
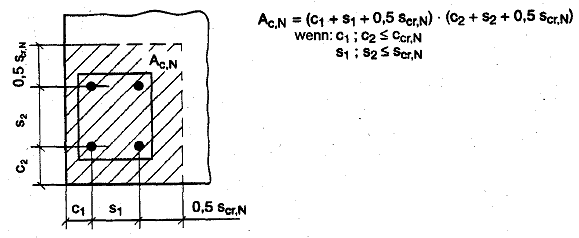
c) Der Einflussfaktor ψs,N berücksichtigt die Störung des rotationssymmetrischen Spannungszustands im Beton durch Bauteilränder. Bei mehreren Bauteilrändern (z.B. bei Verankerungen in der Bauteilecke oder in einem schmalen Bauteil) ist der kleinste Randabstand c in Gleichung (5.2c) einzusetzen.
ψs,N = 0,7 + 0,3 * (c / ccr,N) < 1 (5.2c)
d) Der Schalenabplatzfaktor wre,N berücksichtigt den Einfluss einer Bewehrung.
ψre,N = 0,5 + (hef / 200) < 1 (5.2d)
wobei gilt: hef in [mm]
Sofern im Bereich der Dübelverankerung eine Bewehrung mit einem Achsabstand > 150 mm (unabhängig vom Durchmesser) oder mit einem Durchmesser < 10 mm und einem Achsabstand > 100 mm vorhanden ist, darf unabhängig von der Verankerungstiefe ein Schalenabplatzfaktor ψre,N = 1,0 angesetzt werden.
e) Der Einflussfaktor ψec,N berücksichtigt den Einfluss von unterschiedlichen Zugkräften, die auf die jeweiligen Dübel der Gruppe wirken.
ψec,N = 1 / (1+ 2e N/scr,N) < 1 (5.2e)
eN = Exzentrizität der resultierenden Zugkraft der zugbeanspruchten Dübel (siehe 4.2.1). In den Fällen, in denen eine Exzentrizität in zwei Achsrichtungen vorliegt, ist ψec,N für jede Achsrichtung getrennt zu ermitteln und das Produkt beider Faktoren in Gleichung (5.2) einzusetzen.
Vereinfachend darf ψec,N = 1,0 angenommen werden, wenn der höchstbeanspruchte Dübel nach Gleichung (3.1) (Nh Sd < Nh RSd / γmc) überprüft wird und der Widerstand dieses Dübels angesetzt wird als
Nh Rk,c = .NRk,c / n (5.2f)
wobei n = Anzahl der zugbeanspruchten Dübel
f) Sonderfälle
Bei Verankerungen mit drei oder mehr Rändern mit einem Randabstand cmax < ccr,N (cmax = größter Randabstand) (siehe Bild 5.3) führt die Berechnung nach Gleichung (5.2) zu Ergebnissen, die auf der sicheren Seite liegen.
Genauere Ergebnisse werden erzielt, wenn in Gleichung (5.2a) für hef der Wert
hef = (cmax / ccr,N) * hef oder hef = (Smax / scr,N) hef
eingesetzt wird und bei der Ermittlung von Aoc,N und Ac,N nach den Bildern 5.1 und 5.2 sowie in den Gleichungen (5.2b), (5.2c) und (5.2e) für die Werte
S'cr h = (h`ef / hef) scr,N
c`cr,N = 0,5 S'crN
für scr,N bzw. ccr,N eingesetzt werden.
Bild 5.3 Beispiele für Dübelverankerungen in Bauteilen, in denen hef, scr,N und ccr,N verwendet werden dürfen.
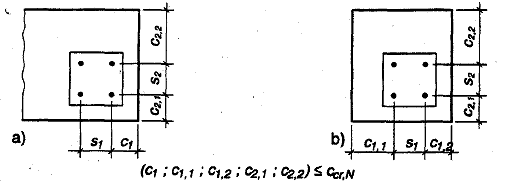
5.2.2.5 Versagen durch Spalten bei Dübelmontage
Ein Spalten des Betons während der Dübelmontage wird vermieden, wenn die in der jeweiligen ETA angegebenen Mindestwerte für Randabstand cmin, Achsabstand smin, Bauteildicke hmin und Bewehrung eingehalten werden.
5.2.2.6 Versagen durch Spalten bei Belastung
Die Werte für Versagen durch Spalten bei Belastung scr,sp und ccr,sp sind in der ETA angegeben.
- Man kann davon ausgehen, dass ein Versagen durch Spalten nicht auftritt, wenn der Randabstand in allen Richtungen c > 1,2 ccr,sp und die Bauteildicke h > 2 hef beträgt.
- Für Dübel, die zur Verwendung in gerissenem Beton geeignet sind, darf die Berechnung des charakteristischen Widerstandes für die Versagensart Spalten des Betons entfallen, wenn die beiden folgenden Bedingungen erfüllt sind:
- Es ist eine Bewehrung vorhanden, die die Rissbreite unter Berücksichtigung der Spaltkräfte nach 7.3 auf wk ~ 0,3 mm begrenzt.
- Der charakteristische Widerstand für Betonausbruch und Versagen durch Herausziehen wird für gerissenen Beton berechnet.
Sind die Bedingungen a) oder b) nicht erfüllt, ist der charakteristische Widerstand eines Einzeldübels oder einer Dübelgruppe für die Versagensart Spalten des Betons nach Gleichung (5.3) zu berechnen.
N Rk,sp = No Rk,c * (Ac,N / Aoc,N) * Ws,N * Wre,N * Wec,N * Wh,sp [N] (5.3)
wobei gilt:
No Rk,c, ψs,N, ψre,N, ψec,N nach Gleichungen (5.2a) bis (5.2g) und Ac,N,/Aoc,N gemäß 5.2.2.4 b), jedoch sind die Werte ccr,N und scr,N durch ccr,sp und scr,sp zu ersetzen.
| ψh,sp | = | Faktor, der den Einfluss der tatsächlichen Bauteildicke h auf die Spaltfestigkeit bei Dübeln berücksichtigt, die den vorliegenden Erfahrungen entsprechen, |
| = | (h / hmin) 2/3 < 1,5 (5.3a) |
Hierbei gilt:
h = tatsächliche Bauteildicke
hmin = Bauteildicke, für die ccr,sp beurteilt wurde
5.2.3 Widerstand bei Querbeanspruchung
5.2.3.1 Erforderliche Nachweise
| Einzeldübel | Dübelgruppe | ||
| Stahlversagen, Querlast ohne Hebelarm | VSd < VRk,s γMs | Vh Sd < VRk,s / γMs | |
| Stahlversagen, Querlast mit Hebelarm | VSd < VRk,s γMs | Vh Sd < VRk,s / γMs | |
| Betonausbruch auf der lastabgewandten Seite | VSd < VRk,cp γMc | Vg Sd < V Rk,cp / γMs | |
| Betonkantenbruch | VSd < V Rk,cp γMc | Vg Sd < V Rk,cp / γMs | |
5.2.3.2 Stahlversagen
a) Querlast ohne Hebelarm
Der charakteristische Widerstand VRk,s eines Dübels bei Stahlversagen ist der jeweiligen ETA zu entnehmen.
Der Wert VRks für Dübel, die den vorliegenden Erfahrungen entsprechen, ergibt sich aus Gleichung (5.4):VRk,s = 0,5 As * fuk [N] (5.4)
Gleichung (5.4) gilt nicht für Dübel mit deutlich reduziertem Querschnitt entlang der Bolzenlänge (z.B. bei Spreizdübeln in Bolzenausführung).
Bei Dübelgruppen ist der in der ETA angegebene charakteristische Querwiderstand mit einem Faktor von 0,8 zu multiplizieren, wenn der Dübel aus Stahl von relativ niedriger Duktilität besteht (Bruchdehnung A5 < 8 %).
b) Querlast mit Hebelarm
Der charakteristische Widerstand VRk,s eines Dübels ergibt sich aus Gleichung (5.5).
VRk,s = (αM * MRk,s) / l [N] (5.5)
wobei
| αM | = | siehe 4.2.2.4 |
| l | = | Hebelarm nach Gleichung (4.2) |
| MRk,s | = | Mo Rks (1 - N Sd/N Rd,s) [Nm] (5.5a) |
| NRd,s | = | NRk,s / γMs |
| NRk,s, γMs | sind der jeweiligen ETA zu entnehmen | |
| Mo Rk,s | = | charakteristischer Widerstand eines Einzeldübels bei Biegebeanspruchung |
Der charakteristische Widerstand Mo Rk,s bei Biegebeanspruchung ist der jeweiligen ETA zu entnehmen.
Der Wert Mo Rk,s, für Dübel, die den vorliegenden Erfahrungen entsprechen, ergibt sich aus Gleichung (5.5b).
Mo Rk,s = 1,2 . Wef * fuk [Nm] (5.5b)
Gleichung (5.5b) ist nur zu verwenden, wenn der Dübel entlang der Bolzenlänge keinen deutlich reduzierten Querschnitt aufweist.
5.2.3.3 Pryout-Versagen (Betonausbruch auf der lastabgewandten Seite)
Bei Verankerungen mit kurzen steifen Dübeln kann es zu einem Betonausbruch auf der lastabgewandten Seite kommen (siehe Bild 5.4). Der entsprechende charakteristische Widerstand VRK,cp darf nach Gleichung (5.6) berechnet werden.
VRk,cp = k * NRk,c (5.6)
Hierbei gilt:
k = aus der jeweiligen ETA zu entnehmender Faktor. NRK,c ist nach 5.2.2.4 für die durch Querlasten beanspruchten Dübel zu ermitteln. Für Dübel, die den vorliegenden Erfahrungen entsprechen und die unter Zugbeanspruchung durch Betonausbruch versagen, liegen die folgenden Annahmen auf der sicheren Seite.
k = 1 hef < 60 mm (5.6c) k = 2 hef > 60 mm (5.6d)
Bild 5.4 Pryout-Versagen (Betonausbruch auf der lastabgewandten Seite)
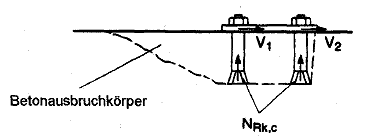
Wenn die Gruppe Querbeanspruchungen und/oder Torsionsmomenten von außen ausgesetzt ist, kann sich die Richtung der einzelnen Querbelastungen ändern. Bild 5.5 veranschaulicht dies für eine Gruppe mit zwei Dübeln, auf die ein Torsionsmoment einwirkt.
Es versteht sich von selbst, dass Gleichung (5.6) in diesen Fällen nicht anwendbar ist. Die Querbeanspruchungen, die auf die einzelnen Dübel wirken, neutralisieren einander, und die Querbeanspruchung, die auf die gesamte Gruppe wirkt, beträgt Vsd = 0.
In Fällen, in denen die horizontalen oder vertikalen Komponenten der Querbeanspruchungen auf die Dübel innerhalb einer Gruppe ihre Richtung ändern, muss anstelle des Nachweises des Pryout-Versagens für die gesamte Gruppe der Nachweis des Pryout-Versagens für den ungünstigsten Dübel der Gruppe erfolgen.
Bei Berechnung des Widerstands des ungünstigsten Dübels sind die Einflüsse der Randabstände sowie der Achsabstände der Dübel zu berücksichtigen. Beispiele für die Berechnung von Ac,N siehe Bild 5.6.
Bild 5.5 Gruppe von Dübeln unter Torsionsmoment; Querlasten, die auf die einzelnen Dübel der Gruppe wirken, ändern ihre Richtungen
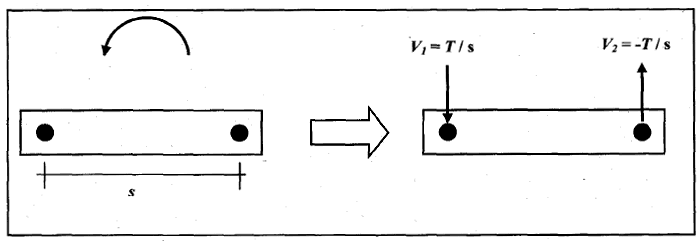
Bild 5.6 Beispiele für die Berechnung der Fläche Ac,N der idealisierten Betonausbruchkörper
a) Gruppe von vier Dübeln ohne Einfluss des Bauteilrandes
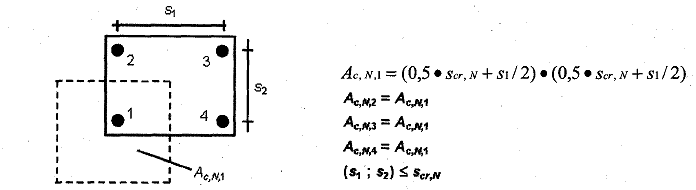
b) Gruppe von zwei Dübeln in der Bauteilecke
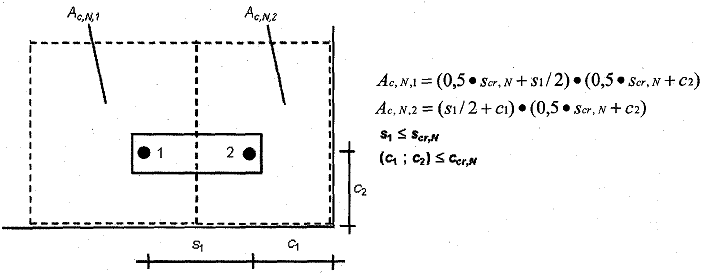
5.2.3.4 Betonkantenbruch
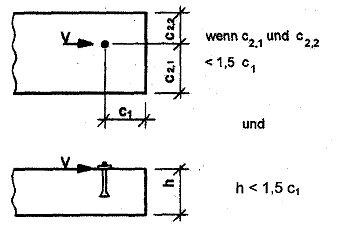
Bei Dübelgruppen mit nicht mehr als 4 Dübeln und einem Randabstand in allen Richtungen von c > 10 hef und c > 60 d darf ein Nachweis des charakteristischen Widerstandes bei Betonkantenbruch entfallen.
Der charakteristische Widerstand eines Dübels oder einer Dübelgruppe bei Betonkantenabbruch beträgt:
V Rk,c = VoRk,c * (Ac,V / Aoc,V) * ψs,V * ψa,V * ψec,V * ψre,V [N] (5.7)
Nachstehend werden die einzelnen Faktoren der Gleichung (5.7) für Dübel angegeben, für die entsprechende Erfahrungen vorliegen:
a) Der Ausgangswert des charakteristischen Widerstandes eines Dübels in gerissenem oder ungerissenem Beton mit Belastung senkrecht zum Rand beträgt:
Vo Rk,c = k1 * dnoma * hßef * √fck,cube C11.5 (5.7a)
dnom, If, C1 [mm]; fck,cube [N/mm2]
Hierbei gilt:
k1 = 1,7 für Anwendungen im gerissenen Beton
k1 = 2,4 für Anwendungen im nicht gerissenen Beton
α = 0,1 * (λ ƒ/ c1) 0,5 (5.7b)
β = 0,1 * (dnom / c1) 0,2 (5.7c)
b) Der geometrische Einfluss des Achsabstandes sowie weiterer Randabstände und der Einfluss der Bauteildicke auf den charakteristischen Widerstand wird durch den Verhältniswert Ac,v/ Aoc,V, berücksichtigt.
Hierbei gilt:
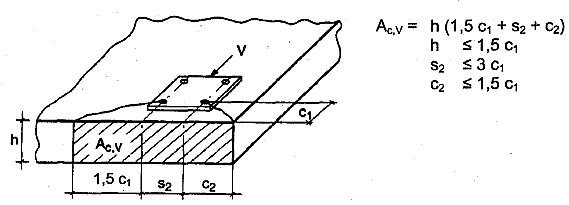
| Aoc,V | = | Fläche des Ausbruchkörpers eines Einzeldübels auf der seitlichen Betonoberfläche ohne Einfluss von Rändern parallel zur angenommenen Lastrichtung, Bauteildicke oder benachbarter Dübel. Dabei wird der Ausbruchkörper als halbe Pyramide mit der Höhe c1 und der Länge der Basisseiten 1,5 c1 und 3 c1 angenommen (Bild 5.7). |
| = | 4,5 c12 (5.7d) | |
| Ac,v | = | vorhandene Fläche des Ausbruchkörpers der Verankerung auf der seitlichen Betonoberfläche. Sie wird begrenzt durch die Überschneidungen der einzelnen Ausbruchkörper benachbarter Verankerungen (s < 3 c1) sowie durch Bauteilränder parallel zur angenommenen Lastrichtung (c2 < 1,5 c1) und Bauteildicke (h < 1,5 c1). Beispiele für die Berechnung von Ac,v siehe Bild 5.8. |
Bei der Berechnung von Aoc,v und Ac,v wird davon ausgegangen, dass die Querlasten senkrecht zum Bauteilrand angreifen.
Bild 5.7 Idealisierter Betonausbruchkörper und Fläche Aoc,v des Ausbruchkörpers eines Einzeldübels
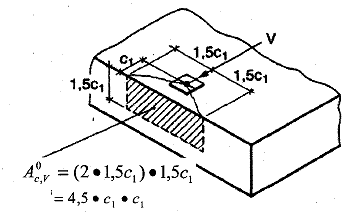
Bild 5.8 Beispiele für vorhandene Flächen der idealisierten Betonausbruchkörper bei verschiedenen Dübelanordnungen unter Querbeanspruchung
a) Einzeldübel in der Bauteilecke
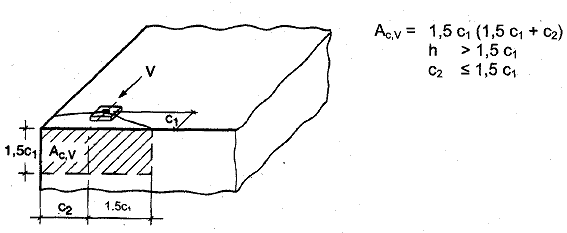
b) Dübelgruppe am Bauteilrand in einem dünnen Bauteil
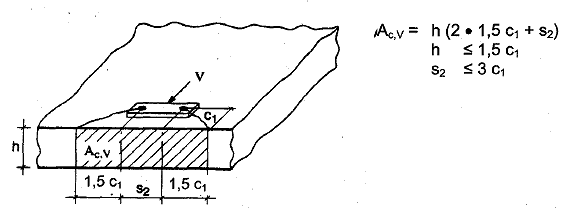
c) Dübelgruppe in der Bauteilecke in einem dünnen Bauteil
c) Der Einflussfaktor ψS,N berücksichtigt die Störung des Spannungszustandes im Beton durch weitere Bauteilränder. Bei Verankerungen mit zwei Randabständen parallel zur angenommenen Lastrichtung (z.B. in einem schmalen Bauteil) ist der kleinere Randabstand in Gleichung (5.7e) einzusetzen.
ψs,v = 0,7 + 0,3 * (c2 / 1,5c1) < 1 (5.7e)
Der Faktor Wh,v berücksichtigt, dass der Querwiderstand nicht proportional zur Bauteildicke, wie beim Verhältnis Ac,v / Aoc,v angenommen, abnimmt.
ψh,v = (1,5c1 /h)1/2 > 1 (5.7f)
e) Der Faktor ψav berücksichtigt den Winkel αv zwischen der einwirkenden Last Vsd und der Richtung senkrecht zur freien Bauteilkante (siehe Bild 4.7b).
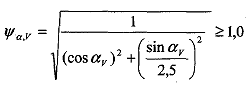 | (5.7g) |
Der Höchstwert av für Gleichung (5.7g) ist auf 90° begrenzt.
Bei αv > 90° ist anzunehmen, dass nur die Komponente der Querlast parallel zum Rand auf den Dübel wirkt. Die weg vom Rand wirkende Komponente kann für den Nachweis bei Betonkantenbruch entfallen. Beispiele für Dübelgruppen, auf die MTd, Vsd oder beide Lasten wirken, sind Bild 5.9 und 5.10 zu entnehmen.
Bild 5.9 Beispiele für Dübelgruppen am Rand, auf die eine Querkraft oder ein Torsionsmoment wirkt
a) Dübelgruppe am Rand, auf die VSd mit einem Winkel αv = 180° wirkt

b) Dübelgruppe am Rand, auf die VSd mit einem Winkel 90 < α < 180° wirkt
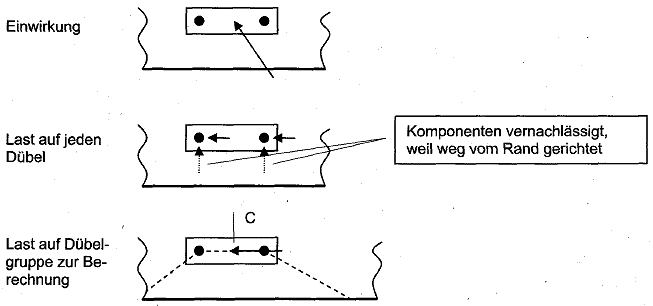
c) Dübelgruppe am Rand, auf die ein Torsionsmoment MTd wirkt
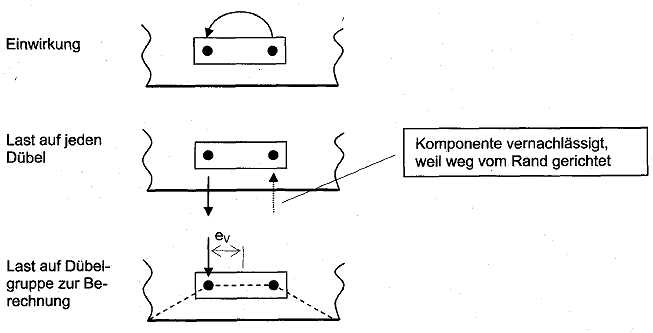
Bild 5.10 Beispiele für Dübelgruppen am Rand, auf die eine Querkraft und ein Torsionsmoment wirkt
a) Querkomponente aufgrund von Torsionsmoment größer als Querkraftkomponente
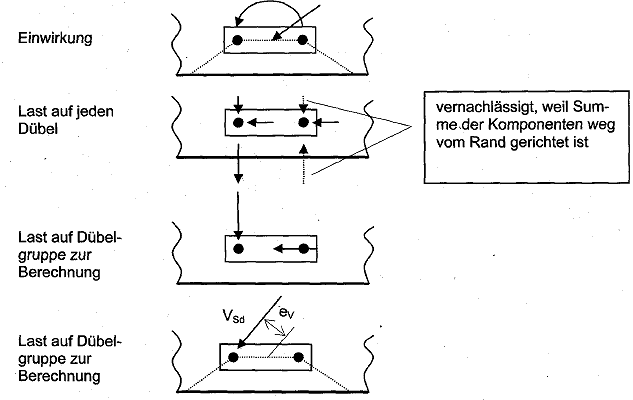
b) Querkomponente aufgrund von Torsionsmoment kleiner als Querkraftkomponente
f) Der Faktor ψec,V berücksichtigt den Einfluss von unterschiedlichen Querlasten, die auf die jeweiligen Dübel der Gruppe wirken.
ψec,V = 1 / (1+ 2ev /(3c1) < 1 (5.7h)
ev = Exzentrizität der resultierenden Querlast der Dübel (siehe 4.2.2).
Der Faktor Wre,V berücksichtigt den Einfluss der Art der Bewehrung im gerissenen Beton.
ψre,V = 1,0 Verankerung im nicht gerissenen Beton und Verankerung im gerissenen Beton ohne Rand- oder Aufhängebewehrung
ψre,V = 1,2 Verankerung im gerissenen Beton mit gerader Randbewehrung (> Ø12 mm)
ψre,V = 1,4 Verankerung im gerissenen Beton mit Rand- und engmaschiger Aufhängebewehrung (a <100 mm)
h) Bei Dübeln, die in einer Ecke sitzen, ist der Widerstand für beide Ränder zu berechnen. Der kleinste Wert ist maßgeblich.
i) Sonderfälle
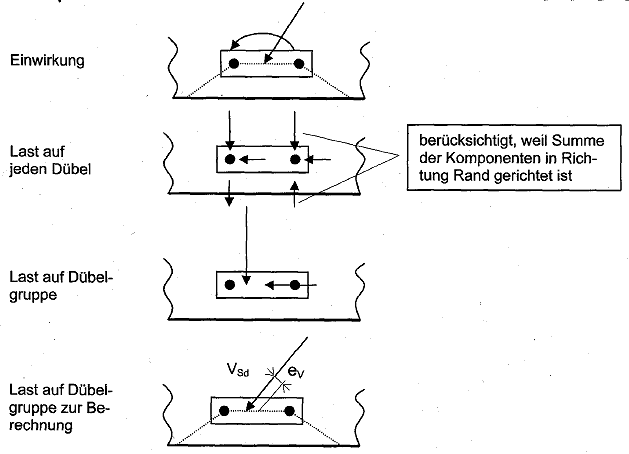
Bei Verankerungen in einem schmalen dünnen Bauteil mit c2max < 1,5 c1 (c2,max = größter Randabstand aus den beiden Randabständen parallel zur Lastrichtung) und h < 1,5 c1 (siehe Bild 5.9) führt die Berechnung nach Gleichung (5.7) zu Ergebnissen, die auf der sicheren Seite liegen.
Genauere Ergebnisse werden erzielt, wenn in den Gleichungen (5.7a) bis (5.7f) und bei der Ermittlung der Flächen Aoc,V, und Ac,v nach den Bildern 5.7 und 5.8 der Randabstand c, durch den Wert c'1 ersetzt wird. Dabei ist c'1 der größere der beiden Werte c2,max/1,5 und h/1,5 bzw. bei Dübelgruppen s2,max/3
Bild 5.11 Beispiel einer Verankerung in einem schmalen dünnen Bauteil, bei dem der Wert c'1 verwendet werden darf.
5.2.4 Widerstand bei kombinierter Zug- und Querbeanspruchung
Bei kombinierten Zug- und Querlasten müssen folgende Gleichungen (siehe Bild 5.12) erfüllt sein:
β N < 1 (5.8a)
βv < 1 (5.8b)
βN +βv < 1,2 (5.8c)
Hierbei gilt:
βN (βv): Verhältnis zwischen Einwirkung und Widerstand bei Zug-(Quer-)beanspruchung.
In Gleichung (5.8) ist jeweils der größte Wert von βN und βv für die einzelnen Versagensarten einzusetzen (siehe 5.2.2.1 und 5.2.3.1).
Bild 5.12 Interaktionsdiagramm für kombinierte Zug- und Querbeanspruchung
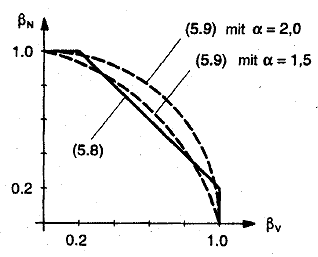
Im Allgemeinen ergeben die Gleichungen (5.8a) bis (5.8c) konservative Ergebnisse. Genauere Ergebnisse werden mit Gleichung (5.9) erzielt:
(βN)a (βV)a < 1 (5.9)
wobei gilt:
βN, βv siehe Gleichung (5.8)
α = 2,0 wenn für NRd und VRd Stahlversagen maßgebend ist
α = 1,5 bei allen anderen Versagensarten
Das Bemessungsverfahren B basiert auf einem vereinfachten Verfahren, bei dem der Bemessungswert des charakteristischen Widerstandes unabhängig von der Belastungsrichtung und der Versagensart angesetzt wird. Bei Dübelgruppen ist nachzuweisen, dass Gleichung (3.1) für den höchstbeanspruchten Dübel eingehalten ist.
Der Bemessungswert des Widerstandes Fo Rd darf ohne Änderung angesetzt werden, wenn der Achsabstand scr und der Randabstand ccr eingehalten sind. FoRd, scr und ccr sind in der jeweiligen ETA angegeben.
Der Bemessungswert des Widerstandes ist nach Gleichung (5.10) zu berechnen, wenn die vorhandenen Werte für Achsabstand und Randabstand kleiner als die Werte scr und ccr und größer oder gleich smin und cmin gemäß ETA sind.
FRd = (1 / n) * (Ac / Aoc) * ψs * ψre * FoRd [N] (5.10)
Hierbei gilt:
N = Anzahl der beanspruchten Dübel
FoRd = Bemessungswert des in der jeweiligen ETA für gerissenen oder nicht gerissenen Beton angegebenen Widerstandes
Der Einfluss des Achsabstandes und des Randabstandes wird durch den Faktor Ac/Aoc und ψs berücksichtigt. Der Faktor Ac/Aoc ist entsprechend 5.2.2.4b und der Faktor ψs entsprechend 5.2.2.4c zu berechnen, wobei Scr,N und ccr,N durch scr und ccr zu ersetzen sind. Der Einfluss einer Bewehrung mit engen Abstand und ungerissenen Beton wird durch den Faktor ψre berücksichtigt. Der Faktor ψre wird berechnet nach 5.2.2.4d).
Bei Querlast mit Hebelarm ist der charakteristische Dübelwiderstand nach Gleichung (5.5) zu berechnen, wobei in Gleichung (5.5a) NRd,s durch Fo Rd zu ersetzen ist.
Der kleinste der Werte von F Rd nach Gleichung (5.10) oder VRk,s/Y Ms nach Gleichung (5.5) ist maßgebend.
Das Bemessungsverfahren C basiert auf einem vereinfachten Verfahren, bei dem unabhängig von der Belastungsrichtung und der Versagensart nur ein Bemessungswert des Widerstandes FRd angesetzt wird. Die vorhandenen Achs- und Randabstände müssen größer oder gleich den Werten von scr und ccr sein. FRd, scr und ccr sind in der jeweiligen ETA angegeben.
Bei Querlast mit Hebelarm ist der charakteristische Dübelwiderstand nach Gleichung (5.5) zu berechnen, wobei in Gleichung (5.5a) NRd,s durch FRd zu ersetzen ist.
Der kleinste Wert von FRd bzw. VRk,s/γMs nach Gleichung (5.5) ist maßgebend.
6 Grenzzustand der Gebrauchstauglichkeit
6.1 Verschiebungen
Die charakteristische Verschiebung des Dübels unter festgelegten Zug- und Querlasten ist aus der ETA zu entnehmen. Es kann davon ausgegangen werden, dass die Verschiebungen linear zur aufgebrachten Last zunehmen. Bei kombinierter Zug- und Querlast sind die Verschiebungen für die Zug- und Querzugkomponenten der resultierenden Last geometrisch zu addieren.
Bei Querlasten ist der Einfluss des Durchgangslochs in der Anschlusskonstruktion auf die erwartete Verschiebung der gesamten Verankerung zu berücksichtigen.
6.2 Querlast mit wechselndem Vorzeichen
Ändern die angreifenden Querlasten mehrfach ihr Vorzeichen, sind geeignete Maßnahmen zu treffen, um einen Ermüdungsbruch des Stahls zu vermeiden (z.B. sollte die Querlast durch Reibung zwischen Anschlusskonstruktion und Beton weitergeleitet werden (z.B. aufgrund einer ausreichend hohen ständigen Vorspannkraft)).
Querlasten mit wechselndem Vorzeichen können aufgrund von Temperaturänderungen in dem befestigten Bauteil (z.B. Fassadenelemente) auftreten. Daher sind diese Bauteile entweder so zu verankern, dass keine signifikanten Querlasten im Dübel aufgrund der im befestigten Bauteil auftretenden Zwangsverformungen auftreten, oder es ist bei Querlast mit Hebelarm (Abstandsmontage) die Biegebeanspruchung in dem höchstbeanspruchten Dübel Δσ = maxσ - minσ im Grenzzustand der Gebrauchstauglichkeit infolge Temperaturschwankungen auf 100 N/mm2 zu begrenzen.
7 Zusätzliche Nachweise zur Sicherung der charakteristischen Bauteiltragfähigkeit
7.1 Allgemeines
Der Nachweis der örtlichen Einleitung der Dübellasten in das Betonbauteil wird durch Anwendung der in diesem Dokument beschriebenen Bemessungsverfahren erbracht.
Die Weiterleitung der Dübellasten in den Verankerungsgrund des Bauteils ist für den Grenzzustand der Tragfähigkeit und den Grenzzustand der Gebrauchstauglichkeit nachzuweisen; hierbei sind die üblichen Nachweise unter Berücksichtigung der durch die Dübel eingeleiteten Lasten durchzuführen. Bei diesen Nachweisen sind die in 7.2 und 7.3 angegebenen zusätzlichen Bestimmungen zu berücksichtigen.
Ist der Randabstand eines Dübels kleiner als der charakteristische Randabstand ccr,N (Bemessungsverfahren A) bzw. ccr (Bemessungsverfahren B und C), muss am Rand des Bauteils im Bereich der Verankerungstiefe eine Längsbewehrung von mindestens Ø 6 vorhanden sein.
Bei Fertigplatten und -balken mit statisch mitwirkender Ortbetonschicht dürfen Dübellasten nur in das Fertigteil übertragen werden, wenn der Fertigbeton mit dem Ortbeton durch eine Verbundbewehrung verbunden ist. Ist eine solche Verbundbewehrung zwischen Fertigteil und Ortbeton nicht vorhanden, müssen die Dübel im Ortbeton mit hef verankert sein. Andernfalls dürfen nur die Lasten von abgehängten Decken oder ähnlichen Konstruktionen mit einer Last bis zu 1,0 kN/m2 in dem Fertigteil verankert werden.
7.2 Quertragfähigkeit des Betonbauteils
Im Allgemeinen sollten die durch Dübellasten erzeugten Querkräfte Vsd,a den folgenden Wert nicht überschreiten:
Vsd,a = 0,4 V Rd1 (7.1)
wobei: V Rd1 = Widerstand bei Querbeanspruchung nach Eurocode EC 2 [1]
Bei der Berechnung von Vsd,a sind die Dübellasten als Punktlasten mit einer Lasteintragungsbreite t1 = st1 2 hef und t2 = st2 + 2 hef mit st1 (st2) Achsabstand zwischen den äußeren Dübeln einer Dübelgruppe in Richtung 1 (2) anzunehmen. Die mitwirkende Breite, über die Querkraft übertragen wird, sollte nach der Elastizitätstheorie berechnet werden.
Auf Gleichung (7.1) kann verzichtet werden, wenn eine der nachfolgenden Bedingungen erfüllt ist.
a) Die durch den Bemessungswert der Beanspruchungen einschließlich der Dübellasten am Untergrund verursachte Querkraft Vsd beträgtVsd < 0,8 V Rd1 (7.2)
b) Unter den charakteristischen Einwirkungen beträgt die resultierende Zuglast Nsk der zugbeanspruchten Verankerungen NskK < 30 kN, und der Achsabstand a zwischen den äußeren Dübeln benachbarter Dübelgruppen oder zwischen den äußeren Dübeln einer Gruppe und Einzeldübeln erfüllt Gleichung (7.3).
a > 200 * √Nsk a [mm]; Nsk [kN] (7.3)
Die Dübellasten werden von einer Aufhängebewehrung aufgenommen, die die Zugbewehrung umschließt und an der gegenüberliegenden Seite des Betonbauteils verankert ist. Ihr Abstand von Einzeldübeln oder von den äußeren Dübeln einer Gruppe muss kleiner sein als hef.
Ist unter den charakteristischen Einwirkungen die resultierende Zuglast Nsk der zugbeanspruchten Verankerungen Nsk > 60 kN, muss entweder die Verankerungstiefe der Dübel hef > 0,8 h betragen oder eine Aufhängebewehrung gemäß Absatz c (s. oben) vorhanden sein.
Die erforderlichen Nachweise zur Sicherung des Querwiderstands des Bauteils sind in Tabelle 7.1 zusammengefasst.
Tabelle 7.1 Erforderliche Nachweise zur Sicherung des Querwiderstands des Bauteils
| Rechnerische Querbeanspruchung des Bauteils unter Berücksichtigung der Dübellasten | Achsabstand zwischen Einzeldübeln und Dübelgruppen | Nsk [kN] | Nachweis der rechnerischen Querlast aus Dübellasten |
| Vsd < 0,8 VRd1 | a > Scr,N 1) (Scr) 2) | < 60 | nicht erforderlich |
| Vsd > 0,8 VRd1 | a > scr,N 1) (scr) 2) und a > 200 √N Sk | < 30 | nicht erforderlich |
| a > scr,N 1) (scr) 2) | < 60 | erforderlich: Vsd,a < 0,4 VRd1 oder Aufhängebewehrung oder hef > 0,8 h | |
| > 60 | nicht erforderlich, jedoch Aufhängebewehrung oder hef > 0,8 h | ||
| 1) Bemessungsverfahren A 2) Bemessungsverfahren B und C | |||
7.3 Widerstand gegen Spaltkräfte
Im Allgemeinen sind die durch Dübel erzeugten Spaltkräfte bei der Bemessung des Bauteils zu berücksichtigen. Dies ist vernachlässigbar, wenn eine der folgenden Bedingungen erfüllt ist.
Der Bereich der Lastabtragung liegt in der Druckzone des Betonbauteils.
Die Zuglastkomponente Nsk der auf die Verankerung (Einzeldübel oder Dübelgruppe) einwirkenden charakteristischen Lasten ist kleiner als 10 kN.
Die Zuglastkomponente Nsk ist nicht größer als 30 kN. Außerdem ist bei Verankerungen in Platten und Wänden eine konzentrierte Bewehrung in beiden Richtungen im Bereich der Verankerung vorhanden. Die Fläche der Querbewehrung muss mindestens 60 % der für die Einwirkungen aufgrund der Dübellasten erforderlichen Längsbewehrung betragen.
Beträgt die auf die Verankerung einwirkende charakteristische Zuglast Nsk > 30 kN und liegen die Dübel in der Zugzone des Betonbauteils, sind die Spaltkräfte durch eine Bewehrung aufzunehmen. Als erste Angabe kann für Dübel, die den vorliegenden Erfahrungen entsprechen, das Verhältnis zwischen Spaltkraft F Sp,k und charakteristischer Zuglast Nsk bzw. N Rd (wegkontrolliert spreizende Dübel) wie folgt angesetzt werden:
| F Sp,k | = 1,5 N Sk | kraftkontrolliert spreizende Dübel (Teil 2) |
| = 1,0 N Sk | Hinterschnittdübel (Teil 3) | |
| = 2,0 N Rd | wegkontrolliert spreizende Dübel (Teil 4) |
Bekanntmachung der Leitlinie für die europäische technische Zulassung für Metalldübel zur Verankerung im Beton
(ETAG 001, Teile 3, 5, 6 und Anhang C)
Vom 28. Oktober 2011
(BAnz Nr. 27a S. 1)
Gemäß § 3 Absatz 1 Satz 2 des Bauproduktengesetzes (BauPG) in der Fassung der Bekanntmachung vom 28. April 1998 (BGBl. I S. 812), das zuletzt durch Artikel 76 der Verordnung vom 31. Oktober 2006 (BGBl. I S. 2407) geändert worden ist, wird die folgende Leitlinie der Europäischen Organisation für Technische Zulassungen EOTA bekannt gemacht. Aufgrund dieser Leitlinie können von dafür. anerkannten Stellen europäische technische Zulassungen nach Artikel 8 der Bauproduktenrichtlinie bzw. § 6 BauPG für Metalldübel zur Verankerung im Beton erteilt werden.
 | ENDE |  |
...
X
⍂
↑
↓