 Für einen individuellen Ausdruck passen Sie bitte die
Für einen individuellen Ausdruck passen Sie bitte dieEinstellungen in der Druckvorschau Ihres Browsers an. Regelwerk
umwelt-online: DIN 1052-1 Holzbauwerke; Berechnung und Ausführung
 Für einen individuellen Ausdruck passen Sie bitte die Für einen individuellen Ausdruck passen Sie bitte dieEinstellungen in der Druckvorschau Ihres Browsers an. Regelwerk |
Holzbauwerke
¨
DIN 1052-1 - Berechnung und Ausführung
Stand 04/1988
(AllMBl. By 1989 S. 635)
1 Anwendungsbereich
Diese Norm gilt für die Berechnung und Ausführung von Bauwerken und von tragenden und aussteifenden Bauteilen aus Holz und Holzwerkstoffen; sie gilt auch für Fliegende Bauten (siehe DIN 4112), Bau- und Lehrgerüste, Absteifungen und Schalungsunterstützungen (siehe DIN 4420 Teil 1 und Teil 2 sowie DIN 4421) und für hölzerne Brücken (siehe DIN 1074), soweit in diesen Normen nichts anderes bestimmt ist.
Für mechanische Holzverbindungen gilt DIN 1052 Teil 2 und für Holzhäuser in Tafelbauart ergänzend DIN 1052 Teil 3.
2 Begriffe
2.1 Voll- und Brettschichtholz
2.1.1 Vollholz
Vollholz sind entrindete Rundhölzer und Bauschnitthölzer (Kanthölzer, Bohlen, Bretter und Latten) aus Nadel- und Laubholz.
2.1.2 Brettschichtholz
Brettschichtholz (BSH) besteht aus mindestens drei breitseitig faserparallel verleimten Brettern oder Brettlagen (siehe auch Abschnitt 12.6) aus Nadelholz.
2.2 Holzwerkstoffe
Holzwerkstoffe im Sinne dieser Norm sind
2.3 Holztafeln, Beplankungen, Dachschalungen
2.3.1 Holztafeln
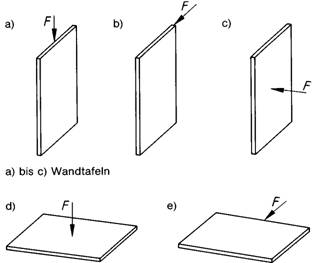
Holztafeln sind Verbundkonstruktionen unter Verwendung von Rippen aus Bauschnittholz, Brettschichtholz oder Holzwerkstoffen und mittragenden oder aussteifenden Beplankungen aus Holz oder Holzwerkstoffen, die ein- oder beidseitig angeordnet sein können. Holztafeln (im folgenden Tafeln genannt) werden als tragende Wand-, Decken- oder Dachtafeln unter Belastungen nach Bild 1 verwendet.
DIN 1052 Teil 1 Seite 3
2.3.2 Beplankungen
Beplankungen sind
2.3.3 Dachschalungen
Dachschalungen sind tragende, flächenartige Bauteile aus Brettern, Bohlen oder Holzwerkstoffen, die die Dachhaut tragen und nur zu Reinigungs- und Instandsetzungsarbeiten begangen werden.
Bild 1. Tragende Tafeln, Belastungsarten
3 Standsicherheitsnachweis und Zeichnungen
3.1 Statische Berechnung
3.1.1 Die statische Berechnung muss übersichtlich und leicht prüfbar sein. Insbesondere sind in ihr auch anzugeben:
3.1.2 Für Bauteile und Verbindungen, die statisch offensichtlich ausreichend bemessen sind, kann auf einen rechnerischen Nachweis verzichtet werden.
3.2 Zeichnungen
3.2.1 Der statischen Berechnung sind in der Regel zeichnerische Unterlagen beizufügen, aus denen insbesondere auch die Maße der tragenden Bauteile und ihrer Querschnittswerte, ferner die Ausbildung der Anschlüsse, Stöße und Verbände, die Anzahl und Anordnung der Verbindungsmittel, erforderliche Überhöhungen und sonstige wichtige Einzelheiten hervorgehen.
3.2.2 Die Anordnung von Verbindungsmitteln in verschiedenen Ebenen, bei Nägeln ihre Kopfseite, muss erforderlichenfalls aus den Zeichnungen ersichtlich sein.
3.3 Baubeschreibung
Angaben, die für die Bauausführung (einschließlich Transport und Montage) oder für die Prüfung der statischen Berechnung und der Zeichnungen notwendig sind, aber aus den Unterlagen nach den Abschnitten 3.1 und 3.2 nicht ersichtlich sind, sind in einer Baubeschreibung zu erläutern.
3.4 Bezeichnungen
In der statischen Berechnung, auf den Zeichnungen und erforderlichenfalls in der Baubeschreibung sind alle Baustoffe und Bauteile mit der Bezeichnung nach der jeweiligen dafür maßgebenden Norm zu bezeichnen.
Die Holzarten nach Tabelle 1 sind zumindest wie folgt zu bezeichnen:
Wird bei der Verwendung von Bau-Furniersperrholz nach DIN 68 705 Teil 3 oder Teil 5 oder von Flachpressplatten nach DIN 68 763 von größeren Rechenwerten des Elastizitäts- oder Schubmoduls nach Tabelle 2 bzw. Tabelle 3, Fußnote 1 ausgegangen, so ist dies zusätzlich zur Normbezeichnung des Holzwerkstoffes deutlich kenntlich zu machen.
Wird bei keilgezinkten Querschnitten beim Spannungsnachweis in den nach Abschnitt 12.3 erlaubten Fällen der Verschwächungsgrad v nicht berücksichtigt, so ist dies auch bei der Bauteilbezeichnung in der statischen Berechnung und auf der Zeichnung deutlich kenntlich zu machen.
Die mechanischen Verbindungsmittel sind mit den für die Berechnung und Ausführung nach DIN 1052 Teil 2 maßgebenden Angaben zu bezeichnen.
Anmerkung: Bei Verwendung von Baustoffen und Bauteilen nach allgemeiner bauaufsichtlicher Zulassung gilt für die Bezeichnung der jeweilige Zulassungsbescheid.
4 Materialkennwerte
4.1 Elastizitäts-, Schub- und Torsionsmoduln
4.1.1 Bei der Berechnung elastischer Formänderungen sind für den Elastizitäts- und Schubmodul bei Voll- und Brettschichtholz die Werte in Tabelle 1, bei Bau-Furniersperrholz nach DIN 68 705 Teil 3 und Teil 5 die Werte in Tabelle 2 und bei Flachpressplatten nach DIN 68 763 die Werte in Tabelle 3 zugrunde zu legen.
Verdrehungen von Voll- und Brettschichtholz dürfen näherungsweise nach der Elastizitätstheorie für isotrope Werkstoffe berechnet werden. Hierbei dürfen die GT-Werte (GT Torsionsmodul) für Vollholz mit 2/3 G, für Brettschichtholz mit GT = G angenommen werden.
4.1.2 Die Werte für die Elastizitäts- und Schubmoduln sind abzumindern
Bei Laubholz der Holzartgruppe C braucht bezüglich der Feuchte keine Abminderung vorgenommen zu werden (siehe Tabelle 1).
Seite 4 DIN 1052 Teil 1
Bei Verwendung von Bau-Furniersperrholz BFU 100 G und von Flachpressplatten V 100 G, in denen eine Feuchte (Feuchtegehalt nach DIN 52 183) von mehr als 18 % über eine längere Zeitspanne (mehrere Wochen) zu erwarten ist, sind die E- und G-Werte für Bau-Furniersperrholz BFU 100 G um 1/4 und für Flachpressplatten V 100 G um 1/3 abzumindern (siehe DIN 68 800 Teil 2).
4.2 Feuchte und Schwindmaße
4.2.1 Als Gleichgewichtsfeuchte im Gebrauchszustand gilt die nach einer gewissen Zeitspanne im Mittel sich einstellende Feuchte des Holzes und der Holzwerkstoffe im fertigen Bauwerk.
Als Gleichgewichtsfeuchte gelten folgende Werte der Holzfeuchte:
| a) bei allseitig geschlossenen Bauwerken | ||
| - mit Heizung | (9 ± 3) % | |
| - ohne Heizung | (12 ± 3) % | |
| b) bei überdeckten, offenen Bauwerken | (15 ± 3) % | |
| c) bei Konstruktionen, die der Witterung | (18 ± 6) % | |
4.2.2 Ist die Holzfeuchte beim Einbau höher als die in Abschnitt 4.2.1 genannten Werte, so darf dieses Holz nur für solche Bauwerke verwendet werden, bei denen es nach-trocknen kann und deren Bauteile gegenüber den hierbei auftretenden Schwindverformungen nicht empfindlich sind.
Tabelle 1. Rechenwerte für Elastizitäts- und Schubmoduln in MN/m2 für Voll- und Brettschichtholz (Holzfeuchte ≤ 20 %)
| Holzart | Elastizitätsmodul | Schubmodul G | ||
| parallel der Faserrichtung E|| | rechtwinklig zur Faserrichtung E  | |||
| 1 | Fichte, Kiefer, Tanne, Lärche, Douglasie, Southern Pine, Western Hemlock1) | 10000 2)3) | 3004) | 500 |
| 2 | Brettschichtholz aus Holzarten nach Zeile 1 | 11000 | 300 | 500 |
| 3 | Laubhölzer der Gruppe | |||
| A Eiche, Buche, Teak, Keruing (Yang) | 12500 | 600 | 1000 | |
| B Afzelia, Merbau, Angelique (Basralocus) | 13000 | 800 | 1000 | |
| C Azobe (Bongossi), Greenheart | 170005) | 12005) | 10005) | |
| 1) Botanische Namen:
Picea abies Karst. (Fichte), Pinus sylvestris L. (Kiefer), Abies alba Mill. (Tanne), Larix decidua Mill. (Lärche), Pseudotsuga menziesii Franco (Douglasie), Pinus palustris (Southern Pine), Tsuga heterophylla Sarg (Western Hemlock).
2) Für Güteklasse III: E||= 8000 MN/m2. 3) Für Baurundholz: E||= 12000 MN/m2. 4) Für Güteklasse III: E 5) Diese Werte gelten unabhängig von der Holzfeuchte. | ||||
Tabelle 2. Rechenwerte für Elastizitäts- und Schubmoduln in MN/m2 für Bau-Furniersperrholz nach DIN 68 705 Teil 3 und Teil 5
| Art der Beanspruchung | Elastizitätsmodul E l)2)3) | Schubmodul G 1)2)4) | |||||
| parallel | rechtwinklig | parallel und rechtwinklig zur Faserrichtung der Deckfurniere | |||||
| zur Faserrichtung der Deckfurniere | |||||||
| Lagenanzahl | Lagenanzahl | Lagenanzahl | |||||
| 3 | ≥ 5 | 3 | ≥ 5 | ≥ 3 | |||
| 1 | Biegung rechtwinklig zur Plattenebene | 8000 | 5500 | 400 | 1500 | 250 (400) | |
| 2 | Biegung, Druck und Zug in Plattenebene | 4500 | 1000 | 2500 | 500 (700) | ||
| 1) Größere Werte dürfen verwendet werden, wenn dies im Rahmen der Überwachung der Herstellung des Bau-Furniersperrholzes durch Prüfzeugnis der fremdüberwachenden Stelle nachgewiesen ist.
2) Für Bau-Furniersperrholz aus Okoume und Pappel sind die Rechenwerte für den Elastizitätsmodul und Schubmodul um 1/5 abzumindern. 3) Für Bau-Furniersperrholz aus Buche nach DIN 68 705 Teil 5 gelten die im Beiblatt 1 zu DIN 68 705 Teil 5 angegebenen Werte. 4) Die Werte in Klammern () gelten für Bau-Furniersperrholz aus Buche nach DIN 68 705 Teil 5. | |||||||
Tabelle 3. Rechenwerte für Elastizitäts- und Schubmoduln in MN/m2 für Flachpressplatten nach DIN 68 763
| Art der Beanspruchung | Elastizitätsmodul E l) | Schubmodul G 1) | ||||||||||||
| Plattennenndicke in mm | Plattennenndicke in mm | |||||||||||||
| bis 13 | über l3 bis 20 | über 20 bis 25 | über 25 bis 32 | über 32 bis 40 | über 40 bis 50 | bis 13 | über l3 bis 20 | über 20 bis 25 | über25 bis 32 | über 32 bis 40 | über40 bis 50 | |||
| 1 | Biegung | rechtwinklig zur Plattenebene | 3200 | 2800 | 2400 | 2000 | 1600 | 1200 | 200 | 100 | ||||
| 2 | in Plattenebene | 2200 | 1900 | 1600 | 1300 | 1000 | 800 | 1100 | 1000 | 850 | 700 | 550 | 450 | |
| 3 | Druck, Zug in Plattenebene | 2200 | 2000 | 1700 | 1400 | 1100 | 900 | - | ||||||
| 1) Größere Werte dürfen verwendet werden, wenn dies im Rahmen der Überwachung der Herstellung der Flachpressplatten durch Prüfzeugnis der fremdüberwachenden Stelle nachgewiesen ist. | ||||||||||||||
4.2.3 Schwind- oder Quellmaße für Holz rechtwinklig zur Faserrichtung und für Holzwerkstoffe in Plattenebene sind in Tabelle 4 angegeben.
4.2.4 Schwinden oder Quellen des Holzes in Faserrichtung braucht nur in Sonderfällen berücksichtigt zu werden (Schwind- und Quellmaß des Holzes in Faserrichtung im Durchschnitt 0,01 %). Das gleiche gilt für Holzwerkstoffe in Plattenebene. Schwinden oder Quellen darf bei Holzwerkstoffen rechtwinklig zur Plattenebene vernachlässigt werden.
4.2.5 Bei behindertem Quellen oder Schwinden dürfen die Werte in Tabelle 4 und in Abschnitt 4.2.4 mit dem halben Betrag berücksichtigt werden.
4.2.6 Holzwerkstoffklassen sind in Abhängigkeit von den zu erwartenden Feuchtebeanspruchungen nach DIN 68 800 Teil 2 zu wählen.
Tabelle 4. Rechenwerte der Schwind- und Duellmaße in %
| Baustoff | Schwind- und Quellmaß für Änderung der Holzfeuchte um 1 % unterhalb des Fasersättigungsbereichs | |
| 1 | Fichte, Kiefer, Tanne, Lärche, Douglasie, Southern Pine, Western Hemlock, Brettschichtholz, Eiche | 0,241) |
| 2 | Buche, Keruing, Angelique, Greenheart | 0,31) |
| 3 | Teak, Afzelia, Merbau | 0,21) |
| 4 | Azobé (Bongossi) | 0,361) |
| 6 | Bau-Furniersperrholz | 0,0202) |
| 7 | Flachpressplatten | 0,0352) |
| 1)Mittel aus den Werten tangential und radial zum Jahrring bzw. zur Zuwachszone.
2) Werte gelten in Plattenebene. | ||
4.3 Kriechverformungen
Beim Durchbiegungsnachweis nach Abschnitt 8.5 sowie bei Verdrehungsberechnungen ist erforderlichenfalls die Kriechverformung infolge der ständigen Last zu berücksichtigen.
Die Kriechverformung darf bei auf Biegung beanspruchten Bauteilen proportional zur elastischen Verformung angenommen werden. Sie ist nachzuweisen, wenn die ständige Last mehr als 50 % der Gesamtlast beträgt.
Für Einfeldträger mit der ständigen Last g und der Gesamtlast q darf die Kriechzahl Φ nach Gleichung (1) berechnet werden.
| Φ = 1 / ηk -1 | (1) |
Bei anderen Tragsystemen und nicht gleichmäßig verteilter Last darf sinngemäß verfahren werden.
In Gleichung (1) ist für Bauteile aus Holz und Bau-Furniersperrholz bei einer Gleichgewichtsfeuchte im Gebrauchszustand ≤ 18 %
| ηk = 3/2 - g/q | (2) |
bei einer Gleichgewichtsfeuchte > 18 %
| ηk = 5/3 - 4/3 g/q | (3) |
einzusetzen.
Für Flachpressplatten sind für Φ die 2fachen Werte in Rechnung zu stellen, sofern ihre Holzfeuchte nicht ständig unter 15 % liegt (siehe DIN 68 800 Teil 2).
Die Abminderung der Elastizitäts- und Schubmoduln nach Abschnitt 4.1.2 ist zu beachten.
Bei Dächern ist der Schneelastanteil von 0,5 (s0 - 0,75) * s/s0 als ständig wirkend anzunehmen; s, s0 bedeuten den Rechenwert der Schneelast bzw. die Regelschneelast nach DIN 1055 Teil 5 in kN/m2.
Bei Wohnhausdächern, ausgenommen Flachdächer, dürfen Kriechverformungen für den Durchbiegungsnachweis vernachlässigt werden.
4.4 Einfluss von Temperaturänderungen
Der Einfluss von Temperaturänderungen darf bei Holz und Holzwerkstoffen in Holzkonstruktionen vernachlässigt werden.
5 Zulässige Spannungen
5.1 Voll- und Brettschichtholz
5.1.1 In Bauteilen aus Bauholz nach DIN 4074 Teil 1 und Teil 2, aus Brettschichtholz sowie aus Laubholz mittlerer Güte sind im Lastfall H die Spannungen nach Tabelle 5 zulässig (wegen Spannungserhöhungen bzw. -ermäßigungen siehe Abschnitte 5.1.5 bis 5.1.12).
5.1.2 Bei aus einzelnen Teilen zusammengesetzten Verbundkörpern sind für die Einstufung in eine der Güteklassen nach DIN 4074 Teil 1 im allgemeinen die Eigenschaften des ganzen Bauteiles, nicht die der einzelnen Teile maßgebend.
Bei auf Biegung oder Biegung mit Normalkraft beanspruchten Bauteilen müssen die Einzelteile in der Zugzone, für sich betrachtet, der Güteklasse entsprechen, deren zulässige Spannung ausgenutzt wird. Bei Bauteilen aus Brettschichtholz gilt dies mindestens für die beiden äußeren Brettlagen im Zugbereich. Bei zusammengesetzten Zuggliedern müssen alle Einzelteile der vorgesehenen Güteklasse entsprechen.
5.1.3 Bei Sparren, Pfetten und Deckenbalken aus Kant-hölzern oder Bohlen dürfen in der Regel die zulässigen Spannungen der Güteklasse I nach Tabelle 5 nicht angewendet werden, bei anderen Bauteilen nur dann, wenn die Anforderungen hinsichtlich Kennzeichnung, Auswahl usw. nach DIN 4074 Teil 1 und Teil 2 erfüllt sind und Berechnung, Durchführung und Ausbildung den strengsten Anforderungen genügen.
5.1.4 Bei Fliegenden Bauten (siehe DIN 4112) dürfen für tragende Bauteile der Haupttragwerke nur Hölzer verwendet werden, die den Bedingungen der Güteklasse I nach DIN 4074 Teil 1 und Teil 2 entsprechen.
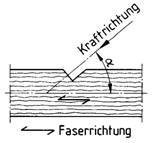
5.1.5 Die zulässigen Druckspannungen bei Kraftrichtung schräg zur Faserrichtung (siehe Bild 2) sind nach der Gleichung
zul σD = zul σD||- (zul σD|| - zul σD = zul σD||- (zul σD|| - zul σD ) * sin α ) * sin α | (4) |
zu berechnen. Dabei ist ± der Winkel zwischen der Kraft- und der Faserrichtung.
Bild 2. Kraftrichtung schräg zur Faserrichtung
5.1.6 Im Lastfall HZ (siehe Abschnitt 6.2.2) dürfen die zulässigen Spannungen nach Tabelle 5 um 25 %, bei waagerechten Stoßlasten nach DIN 1055 Teil 3 und Erdbebenlasten nach DIN 4149 Teil 1 um 100 % und für Transport- und Montagezustände um 50 % erhöht werden (für mechanische Verbindungen siehe DIN 1052 Teil 2, Abschnitt 3.2).
5.1.7Berücksichtigung von Feuchteeinwirkungen
Die Werte für die Spannungen in Tabelle 5 sind abzumindern
Tabelle 5. Zulässige Spannungen für Voll- und Brettschichtholz in MN/m2 im Lastfall H
| Art der Beanspruchung | Vollholz (aus Holzarten nach Tabelle 1, Zeile 1) | Brettschichtholz (aus Holzarten nach Tabelle 1, Zeile 1) nach Abschnitt 12.6 Güteklasse nach DIN 4074 Teil 1 | Vollholz (aus Laubhölzern nach Tabelle1) Holzartgruppe | |||||||
| nach Güteklasse DIN 4074 Teil 1 und Teil 2 | ||||||||||
| A | B | C | ||||||||
| III | II | I | II | I | mittlere Güte 1) | |||||
| 1 | Biegung | zul oB | 7 | 10 | 13 | 11 | 14 | 11 | 17 | 25 |
| 2 | Zug | zul oZ|| | 0 | 8,5 | 10,5 | 8,5 | 10,5 | 10 | 10 | 15 |
| 3 | Zug | zul oZ | 0 | 0,05 | 0,05 | 0,2 | 0,2 | 0,05 | 0,05 | 0,05 |
| 4 | Druck | zul oD|| | 6 | 8,5 | 11 | 8,5 | 11 | 10 | 13 | 20 |
| 5a | Druck | zul oD | 2 | 2 | 2 | 2,5 | 2,5 | 3 | 4 | 8 |
| 5b | 2,52) | 2,52) | 2,52) | 3,02) | 3,02) | 42) | - | - | ||
| 6 | Abscheren | zul τa | 0,9 | 0,9 | 0,9 | 0,9 | 0,9 | 1 | 1,4 | 2 |
| 7 | Schub aus Querkraft | zul τQ | 0,9 | 0,9 | 0,9 | 1,2 | 1,2 | 1 | 1,4 | 2 |
| 8 | Torsion3) | zul τT | 0 | 1 | 1 | 1,6 | 1,6 | 1,6 | 1,6 | 2 |
| 1) Mindestens Güteklasse II im Sinne von DIN 4074 Teil 1 und Teil 2.
2) Bei Anwendung dieser Werte ist mit größeren Eindrücken zu rechnen, die erforderlichenfalls konstruktiv zu berücksichtigen sind. Bei Anschlüssen mit verschiedenen Verbindungsmitteln dürfen diese Werte nicht angewendet werden. 3) Für Kastenquerschnitte sind die Werte nach Zeile 7 einzuhalten | ||||||||||
Die Abminderungen gelten nicht für Laubhölzer der Holzartgruppe C und für Fliegende Bauten, die einen Schutzanstrich besitzen, der in Abständen von höchstens zwei Jahren zu erneuern ist.
5.1.8 Bei Durchlaufträgern ohne Gelenke darf die Biegespannung über den Innenstützen die zulässigen Werte nach Tabelle 5, Zeile 1, um 10 % überschreiten. Dies gilt nicht bei Sparren von Kehlbalkenbindern mit verschieblichen Kehlbalken.
5.1.9 Bei Rundhölzern dürfen in den Bereichen ohne Schwächung der Randzone die zulässigen Biege- und Druckspannungen in Tabelle 5, Zeilen 1 und 4, um 20 % erhöht werden.
5.1.10 Bei genagelten Zugstößen oder -anschlüssen sind die nach Tabelle 5, Zeile 2, zulässigen Zugspannungen in denjenigen Stoß- und Anschlussteilen um 20 % abzumindern, die nicht nach Abschnitt 7.3 für die 1,5fache anteilige Zugkraft zu bemessen sind.
5.1.11 Bei Druck rechtwinklig zur Faserrichtung muss der Überstand ü von Trägern und Schwellen über die Druckfläche in Faserrichtung einseitig bzw. beiderseits mindestens 100 mm bei h > 60 mm und mindestens 75 mm bei h ≤ 60 mm betragen. Zwischen zwei Druckflächen ist ein Abstand von mindestens 150 mm einzuhalten.
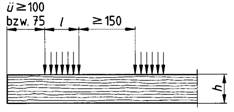
Bei Druckflächen mit einer Länge l in Faserrichtung < 150 mm (siehe Bild 3) darf dann die zulässige Druckspannung nach Tabelle 5, Zeile 5a mit dem Faktor
kD = (150/l)0,25 = (150/l)0,25 | (5) |
vervielfacht werden (l Länge der Druckfläche in mm), höchstens jedoch mit kD = 1,8.
= 1,8.
Bild 3. Belastungsanordnung für kurze Druckflächen
Sofern die im ersten Absatz genannten Überstände unterschritten werden, sind die in Tabelle 5, Zeilen 5a und 5b angegebenen zulässigen Spannungen mit kD = 0,8 abzumindern.
= 0,8 abzumindern.
5.1.12 Bei durchlaufenden oder auskragenden Biegebalken aus Nadelholz und Laubholz der Holzartgruppe A dürfen die zulässigen Schubspannungen aus Querkraft nach Tabelle 5, Zeile 7, in Bereichen, die mindestens 1,50 m vom Stirnende entfernt liegen, auf zul τQ = 1,2 MN/m2 erhöht werden.
5.2 Holzwerkstoffe
5.2.1 In Bauteilen aus Holzwerkstoffen sind im Lastfall H die Spannungen nach Tabelle 6 zulässig.
Für Bau-Furniersperrholz nach DIN 68 705 Teil 3 betragen die zulässigen Spannungen in Plattenebene bei 30° ≤ α ≤ 60° oZ,D = 2 MN/m2. Dabei ist A der Winkel zwischen Kraft- und Faserrichtung der Deckfurniere. Für 0° ≤ α ≤ 30° darf zwischen 8 MN/m2 und 2 MN/m2, für 60° ≤ α ≤ 90° darf zwischen 2 MN/m2 und 4 MN/m2 geradlinig interpoliert werden.
5.2.2 Abschnitt 5.1.6 gilt sinngemäß.
5.2.3 Berücksichtigung von Feuchteeinwirkungen
Bei Verwendung von Bau-Furniersperrholz BFU 100 G und von Flachpressplatten V 100 G, in denen eine Feuchte von mehr als 18 % über mehrere Wochen zu erwarten ist, sind die zulässigen Spannungen für Bau-Furniersperrholz BFU 100 G um 1/4 und für Flachpressplatten V 100 G um 1/3 abzumindern.
5.3 Andere Baustoffe
5.3.1 Für andere Baustoffe gelten die entsprechenden Normen.
5.3.2 Für geschweißte Bauteile aus Stahl gilt DIN 18 800 Teil 7.
5.3.3 Bei geraden Bauteilen aus Flach- und Rundstahl, für die keine Bescheinigung DIN 50 049 - 2.1 (Werksbescheinigung) vorliegt, dürfen die Zug- und Biegespannungen im Lastfall H und HZ höchstens 110 MN/m2, im Kernquerschnitt der Rundstähle höchstens 100 MN/m2 betragen.
5.3.4 Bezüglich des Korrosionsschutzes von Stahlteilen sind DIN 55 928 Teil 1, Teil 2, Teil 4, Teil 5, Teil 6 und Teil 8 und von Teilen aus Aluminium DIN 4113 Teil 1 zu beachten.
6 Allgemeine Bemessungsregeln
6.1 Allgemeines
Auf die räumliche Aussteifung der Bauteile und ihre Stabilität ist besonders zu achten. Die bei Versagen oder Ausfall eines Bauteiles auftretenden Folgen für die Standsicherheit der Gesamtkonstruktion sind zu beachten und gegebenenfalls durch geeignete Maßnahmen einzugrenzen.
6.2 Lastannahmen
6.2.1 Lasten
Die Lastannahmen für den Standsicherheitsnachweis richten sich nach den entsprechenden Normen.
Die auf ein Tragwerk wirkenden Lasten werden eingeteilt in Haupt-, Zusatz- und Sonderlasten.
Hauptlasten sind:
Zusatzlasten sind:
Sonderlasten sind:
6.2.2 Lastfälle
Für den Standsicherheitsnachweis werden folgende Lastfälle unterschieden:
Wird ein Bauteil, abgesehen von seiner Eigenlast, nur durch Zusatzlasten beansprucht, so gilt die größte davon als Hauptlast.
Die Einzellast (Mannlast) nach DIN 1055 Teil 3 ist immer als Zusatzlast einzustufen.
Für die Berücksichtigung von waagerechten Stoßlasten und Erdbebenlasten gilt Abschnitt 5.1.6.
6.3 Mindestquerschnitte
6.3.1 Tragende einteilige Einzelquerschnitte von Vollholzbauteilen müssen eine Mindestdicke von 24 mm und mindestens 14 cm2 Querschnittsfläche (11 cm2 für Lattungen) haben, soweit nicht wegen der Verbindungsmittel größere Mindestmaße erforderlich sind.
Maße der für Brettschichtholz verwendeten Einzelbretter siehe Abschnitt 12.6.
6.3.2 Mindestdicken für Tafeln siehe Abschnitt 11.1.1.
6.3.3 Die Mindestdicke tragender Platten aus Holzwerkstoffen beträgt für Flachpressplatten 8 mm, für Bau-Furniersperrholz 6 mm. Bau-Furniersperrholz muss, sofern es nur Aussteifungszwecken dient, aus mindestens drei Lagen, für alle sonstigen tragenden Bauteile aus mindestens fünf Lagen bestehen.
6.4 Querschnittsschwächungen
6.4.1 Baumkanten, die nicht breiter sind als in DIN 4074 Teil 1 zugelassen, brauchen nicht berücksichtigt zu werden.
6.4.2 In Zugstäben und in der Zugzone von auf Biegung beanspruchten Bauteilen sind beim Spannungsnachweis alle Querschnittsschwächungen (Bohrungen, Einschnitte durch Versatz und dergleichen) zu berücksichtigen. In Faserrichtung hintereinander liegende Schwächungen sind nur einmal in Rechnung zu stellen. Dies gilt auch für versetzt zur Faserrichtung angeordnete Schwächungen mit einem lichten Abstand > 150 mm bzw. bei stabförmigen Verbindungsmitteln ≥ 4 d.
Bei Keilzinkenverbindungen nach DIN 68 140 braucht die Schwächung durch den Zinkengrund nur einmal berücksichtigt zu werden (siehe Abschnitt 12.3). Querschnittsschwächungen durch Stabdübel und Passbolzen sind mit ihrem Durchmesser dst zu berücksichtigen, bei Bolzen ist der Durchmesser des Bohrloches (db + 1 mm) maßgebend.
Bei Dübelverbindungen mit Einlass- und Einpressdübeln sind außer dem Bohrloch des zugehörigen Bolzens entsprechende Fehlflächen abzuziehen (Beispiel für Querschnittsschwächung bei zweiseitigen Ringkeildübeln siehe Bild 4).
Für Dübelverbindungen besonderer Bauart sind die Fehlflächen ΔA aus DIN 1052 Teil 2, Tabellen 4, 6 und 7, zu entnehmen.
Querschnittschwächungen durch Nägel sind bei vorgebohrten Nagellöchern mit dem Nageldurchmesser zu berücksichtigen. Dies gilt für Nägel mit Durchmesser > 4,2 mm auch bei nicht vorgebohrten Nagellöchern sowie stets für Nägel in Bau-Furniersperrholz.
Tabelle 6. Zulässige Spannungen für Holzwerkstoffe in MN/m2 im Lastfall H
| Art der Beanspruchung | Bau-Furniersperrholz nach DIN 68 705 Teil 3 und Teil 51) | Flachpressplatten nach DIN 68 763 | |||||||||||
| parallel | rechtwinklig | Plattennenndicke mm | |||||||||||
| zur Faserrichtung der Deckfurniere | |||||||||||||
| Lagenanzahl | Langenanzahl | ||||||||||||
| 3 | ≥ 5 | 3 | ≥ 5 | bis 13 | über 13 bis 20 | über 20 bis 25 | über 25 bis 32 | über 32 bis 40 | über 40 bis 50 | ||||
| 1 | Biegung rechtwinklig zur Plattenebene | zul σBxy | 13 | 5 | 4,5 | 4,0 | 3,5 | 3,0 | 2,5 | 2,0 | |||
| 2 | Biegung in Plattenebene | zul σBxy | 9 | 6 | 3,4 | 3,0 | 2,5 | 2,0 | 1,6 | 1,4 | |||
| 3 | Zug in Plattenebene | zul σZx | 8 | 4 | 2,5 | 2,25 | 2,0 | 1,75 | 1,5 | 1,25 | |||
| 4 | Druck in Plattenebene | zul σDx | 8 | 4 | 3,0 | 2,75 | 2,5 | 2,25 | 2,0 | 1,75 | |||
| 5 | Druck rechtwinklig zur Plattenebene | zul σDz | 3 (4,5) | 3 (4,5) | 2,5 | 2,5 | 2,5 | 2,0 | 1,5 | 1,5 | |||
| 6 | Abscheren in Plattenebene und in Leimfugen | zul τzx2) | 0,9 (1,2) | 0,9 (1,2) | 0,4 | 0,4 | 0,4 | 0,3 | 0,3 | 0,3 | |||
| 7 | Abscheren rechtwinklig zur Plattenebene | zul τyx2) | 1,8 (3) | 3 (4) | 1,8 (3) | 3 (4) | 1,8 | 1,8 | 1,8 | 1,2 | 1,2 | 1,2 | |
| 8 | Lochleibungsdruck3)4) | zul σl | 8 | 4 | 6,0 | 6,0 | 6,0 | 6,0 | 6,0 | 6,0 | |||
| 1) Die Werte in Klammern () gelten für Bau-Furniersperrholz nach DIN 68 705 Teil 5 und Beiblatt 1 zu DIN 68 705 Teil 5. Die übrigen Werte für die zulässigen Spannungen dürfen aus den Festigkeitswerten in DIN 68 705 Teil 5 mit dem Sicherheitsbeiwert 3 berechnet werden.
2) Werte gelten auch für Schub aus Querkraft. 3) Für Bolzen und Stabdübel. 4) Für Bau-Furniersperrholz nach DIN 68 705 Teil 5 aus mindestens fünf Lagen ist zul ol = 2 * zul oDx. | |||||||||||||
Bild 4. Querschnittsschwächung bei Ringkeildübelverbindungen ΔΑ = (dd-(db+1)) * hd/2

Querschnittsschwächungen durch Schrauben sind mit dem Schaftdurchmesser zu berücksichtigen.
6.4.3 Bei Druckstäben und in der Druckzone von auf Biegung beanspruchten Bauteilen brauchen Querschnittsschwächungen für den gewöhnlichen Spannungsnachweis nur dann berücksichtigt zu werden, wenn die geschwächte Stelle nicht satt ausgefüllt ist oder der ausfüllende Baustoff einen geringeren Elastizitätsmodul als der geschwächte Baustoff aufweist (z.B. wenn die Faserrichtung von Holzeinlagen rechtwinklig oder schräg zu der des Druckstabes verläuft).
6.4.4 Wenn durch Querschnittsschwächungen wesentliche ausmittige Kraftwirkungen entstehen, sind sie statisch in Rechnung zu stellen.
6.5 Wechselbeanspruchte Bauteile
6.5.1 Stäbe, bei denen der Vorzeichenwechsel der Beanspruchung nicht allein aus Wind- und Schneelasten herrührt, sind für
| zul σ = kw * zul σ | (6) |
mit
| kw = 1 - 0,25 | min. |σ| | (7) |
| max.|σ| |
zu bemessen, wobei für min |o| bzw. max. |o| jeweils die Spannung mit dem kleinsten bzw. größten Absolutbetrag einzusetzen ist.
6.5.2 Stöße und Anschlüsse sind sinngemäß zu bemessen.
6.6 Ausmittige Anschlüsse
Spannungen, die durch ausmittige Anschlüsse entstehen, sind besonders zu berücksichtigen.
Fachwerkstäbe sind möglichst mittig anzuschließen. Spannungen, die durch Ausmittigkeiten hervorgerufen werden, brauchen bei Nagelverbindungen nach Bild 5a und bei Verbindungen mit Nagel- oder Knotenplatten nach Bild 5b in der Regel nicht nachgewiesen zu werden, wenn die Ausmittigkeit e1 bzw. e2 nicht größer als die halbe Gurthöhe ist.
7 Bemessungsregeln für Zugstäbe
7.1 Mittiger Zug
Für planmäßig mittig beanspruchte Zugstäbe ist der Spannungsnachweis unter Berücksichtigung der Querschnittsschwächungen nach Abschnitt 6.4 durchzuführen:
| N / An | ≤ 1 | (8) |
| zul σZ|| |
Bild 5. Ausmittiger Stabanschluss
a) bei genagelten Brett- und Bohlenbindern

b) bei Bindern mit Nagel- oder Knotenplatten

Hierin ist An die nutzbare Querschnittsfläche, für zul ÃZ' sind die maßgebenden Werte nach Tabelle 5 bzw. Tabelle 6 einzusetzen.
7.2 Ausmittiger Zug (Zug und Biegung)
Für Zugstäbe, die planmäßig ausmittig oder zusätzlich quer zur Stabachse beansprucht werden, ist nachzuweisen, dass die Bedingung
| N / An | + | M / Wn | ≤ 1 | (9) |
| zul σZ|| | zul σZB |
eingehalten ist.
Hierin ist Wn das nutzbare Widerstandsmoment.
Für zul oZ|| bzw. zul oZB sind die maßgebenden Werte nach Tabelle 5 bzw. Tabelle 6 einzusetzen.
7.3 Stöße und Anschlüsse
Stöße und Anschlüsse sind in der Regel symmetrisch zu der bzw. den Stabachsen auszuführen. Dabei sind einseitig beanspruchte Holz- und Holzwerkstoffteile für die 1,5fache anteilige Zugkraft zu bemessen.
8 Bemessungsregeln für biegebeanspruchte Bauglieder
8.1 Grundlagen
8.1.1 Stützweiten
8.1.1.1 Als Stützweite l ist der Abstand der Auflagermitten in Rechnung zu stellen. Bei Auflagerung auf Mauerwerk oder Beton ist als Stützweite der Abstand der Auflagermitten, bei Einfeldträgern jedoch höchstens das 1,05fache der lichten Weite, anzunehmen.
8.1.1.2 Durchlaufende Bretter, Bohlen oder Platten aus Holzwerkstoffen sind in der Regel als frei drehbar gelagerte Träger auf zwei Stützen zu berechnen.
Bei Dach- und Deckenschalungen darf die Durchlaufwirkung rechnerisch berücksichtigt werden, wenn etwaige Stöße im einzelnen planmäßig festgelegt werden.
8.1.1.3 Für Pfetten und Balken mit Kopfbändern oder Sattelhölzern gilt Abschnitt 8.2.4.
8.1.2 Auflagerkräfte
Die Auflagerkräfte von Durchlaufträgern (auch Netten) dürfen im allgemeinen wie für Einfeldträger berechnet werden, sofern das Verhältnis benachbarter Spannweiten zwischen 2/3 und 3/2 liegt. Ausgenommen davon sind Zwei-feldträger.
8.1.3 Stöße
An Stoßstellen ist die Übertragung der Schnittgrößen durch Stoßdeckungsteile und Verbindungsmittel sicherzustellen. Bei Verformungsberechnungen und bei der Berechnung statisch unbestimmter Systeme ist erforderlichenfalls die Steifigkeit unter Berücksichtigung sowohl der Stoßdeckungsteile als auch der Nachgiebigkeit der Verbindungsmittel an der Stoßstelle zu bestimmen. Bei Druckgurten von Vollwandträgern ist das erforderliche Flächenmoment 2. Grades durch die Stoßdeckungsteile zu ersetzen, wobei die Verbindungsmittel bei Anordnung von Kontaktstößen für die halbe Druckkraft bemessen werden dürfen.
8.1.4 Lasteintragungsbreiten
Wird bei Platten aus Holzwerkstoffen, die miteinander durch Nut und Feder oder gleichwertige Maßnahmen verbunden sind, ein Nachweis für die Aufnahme der Einzellast von 1 kN (Mannlast, siehe DIN 1055 Teil 3) geführt, so dürfen bei Dach- und unmittelbar belasteten Deckenschalungen sowie bei oberen Dach- und Deckenbeplankungen in der Regel die jeweils größten Lasteintragungsbreiten t nach Tabelle 7 als mitwirkende Plattenbreite angesetzt werden.
Bei Dach- und Deckenschalungen aus Brettern oder Bohlen, die miteinander durch Nut und Feder oder gleichwertige Maßnahmen verbunden sind, darf unabhängig von der Breite des Einzelteiles für die Lasteintragungsbreite t = 0,35 m und bei nicht verbundenen Brettern oder Bohlen t = 0,16 m angesetzt werden.
Tabelle 7. Lasteintragungsbreiten t für Platten aus Holzwerkstoffen
| Plattenbreite b | Platten miteinander | ||
| verbunden | nicht verbunden | ||
| 1 | ≥ 0,35 m1) | 0,35 m | 0,35 m |
| 2 | ≥ 1 m1) | 0,70 m | 0,35 m |
| 3 | > Stützweite l | 0,7 l | 0,35 l |
| 4 | ≤ Stützweite l | 0,7 b | 0,35 b |
| 1) Stützweite l beliebig | |||
8.2 Biegeträger aus Voll- und Brettschichtholz
8.2.1 Bemessung
8.2.1.1 Bemessung für Biegung
Für auf Biegung beanspruchte Bauteile ist der Spannungsnachweis unter Berücksichtigung der Querschnittsschwächungen nach Abschnitt 6.4 durchzuführen:
| M / Wn | ≤ 1 | (10) |
| zul σB |
Hierin ist Wn das nutzbare Widerstandsmoment, für zul oB sind die maßgebenden Werte nach Tabelle 5, Zeile 1, einzusetzen.
Bei zusammengesetzten Biegeträgern darf außerdem die Schwerpunktsspannung in den gezogenen Gurtteilen die Werte in Tabelle 5, Zeile 2, nicht überschreiten.
Ferner ist der Nachweis gegen seitliches Ausweichen nach Abschnitt 8.6 zu führen.
8.2.1.2 Bemessung für Querkraft
Für Biegeträger mit Auflagerung am unteren Trägerrand und Lastangriff am oberen Trägerrand braucht der Nachweis der Schubspannungen und gegebenenfalls der Schubverbindungsmittel im Bereich von End- und Zwischenauflagern, wenn dort keine Ausklinkungen und Durchbrüche sind, nicht mit der vollen Querkraft geführt zu werden. Als maßgebend darf die Querkraft im Abstand von h / 2 (h Trägerhöhe über Auflagermitte, auch bei Abschrägungen) vom Auflagerrand angenommen werden.
Für eine Einzellast im Abstand A ≥ ao = 2h von der Auflagermitte ist der volle Wert der Querkraft der Bemessung zugrunde zu legen, für A < 2h darf der mit ao anstelle von A ermittelte und im Verhältnis A / (2h) abgeminderte Anteil als maßgebende Querkraft in Rechnung gestellt werden.
Für den Nachweis der Schubspannungen sind die zulässigen Werte in Tabelle 5, Zeile 7, maßgebend.
8.2.1.3 Bemessung für Torsion und Querkraft
Ein Nachweis der Wirkungen bei Torsionsbeanspruchung braucht nicht geführt zu werden, wenn die Torsion zur Erhaltung des Gleichgewichtes nicht notwendig ist, z.B. bei Sparren, Pfetten und Balken üblicher Dach- und Deckenkonstruktionen.
Der Nachweis der Torsionsspannungen darf näherungsweise nach der Elastizitätstheorie für isotrope Werkstoffe geführt werden. Die so ermittelten Schubspannungen dürfen die Werte nach Tabelle 5, Zeile 8, nicht überschreiten.
Bei gleichzeitiger Wirkung von Schubspannungen aus Torsion und Querkraft muss die Bedingung
| τT | + | ( | τQ | )m | ≤ 1 | (11) |
| zul τT | zul τQ |
eingehalten werden, wobei für Nadelholz m = 2 und für Laubholz m = 1 zu setzen ist.
Hierin bedeuten:
| τT | Schubspannung aus Torsion |
| τQ | Schubspannung aus Querkraft |
| zul τQ | zulässige Schubspannung aus Querkraft nach Tabelle 5, Zeile 7 |
| zul τT | zulässige Schubspannung aus Torsion nach Tabelle 5, Zeile B. |
8.2.2 Ausklinkungen und Durchbrüche bei Biegeträgern mit Rechteckquerschnitt aus Nadelholz
8.2.2.1 Ausklinkungen und Zapfen
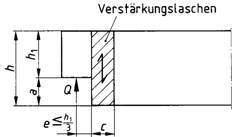
Bei rechtwinklig oder schräg ausgeklinkten Trägerenden und bei Trägern mit Zapfen nach Bild 6 ist die zulässige Querkraft nach Gleichung (12) zu berechnen:
| zul Q = 2/3 * b * h1 * kA * zul τQ | (12) |
Hierin bedeuten:
| b | Breite des Trägers |
| zul rQ | zulässige Schubspannung aus Querkraft nach Tabelle 5, Zeile 7 |
| kA | Abminderungsfaktor wegen gleichzeitiger Wirkung von Schub- und Querzugspannungen. |
Die Ausklinkung muss die Bedingungen A / h ≤0,5 und A ≤ 0,50 m erfüllen. Hierin bedeuten A die Ausklinkungshöhe und h die Trägerhöhe.
Für rechtwinklige Ausklinkungen ohne Verstärkung (siehe Bild 6a) ist
| kA = 1 - 2,8 a/h | (13) |
einzusetzen, mindestens jedoch kA = 0,3.
Für rechtwinklige Ausklinkungen mit Verstärkung (siehe Bild 6b) darf kA = 1 gesetzt werden.
Die Verstärkung darf näherungsweise für die Zugkraft
| Z = 1,3 Q * [3 (a/h)2 - 2 (a/h)3] | (14) |
bemessen werden.
Als Verstärkungen dürfen mit Resorcinharzleim aufgeleimte Laschen aus Bau-Furniersperrholz aus mindestens fünf Lagen nach DIN 68 705 Teil 5 der Klasse 100 verwendet werden. Nagelpressleimung ist zulässig (siehe Abschnitt 12.5). Die Verstärkungslaschen sind beidseitig anzuordnen. Ihre Breite c muss der Bedingung 0,25 A ≤ c ≤ 0,50 A genügen.
Als zulässige Spannungen sind zul σZ|| = 4 MN/m2 im Bau-Furniersperrholz und zul τa = 0,25 MN/m2 in der Leimfläche anzunehmen.
Bild 6. Unten ausgeklinkte Träger und Träger mit Zapfen
a) Rechtwinklige Ausklinkung ohne Verstärkung

b) Rechtwinklige Ausklinkung mit Verstärkung
c) Zapfen

d) Schräge Ausklinkung

Träger bis zu 300 mm Höhe mit Zapfen nach Bild 6c dürfen nach den Gleichungen (12) und (13) berechnet werden, wobei h1 = 2/3 h zu setzen ist, soweit kein genauerer Nachweis erfolgt.
Bei Ausklinkungen mit geneigtem Trägerrand (siehe Bild 6d) darf kA =1 gesetzt werden, wenn die Länge s ≥ 14 A bei Güte-klasse I und ≥ 10 A bei Güteklasse II oder s ≥ 2,5 * h beträgt. Der kleinere Wert ist maßgebend. Die Bedingung A ≤ 0,50 m gilt für diese Ausklinkungen nicht.
Die Spannungskombination am geneigten Trägerrand ist zu beachten (siehe Abschnitt 8.2.3.4).
Bei oben ausgeklinkten oder abgeschrägten Trägerenden nach Bild 7 ist die zulässige Querkraft nach Gleichung (15) zu berechnen:
| zul Q = 2/3 b * [h - a/h1 * e] * τQ | (15) |
Die Ausklinkung bzw. Abschrägung muss folgende Bedingungen erfüllen:
a/h ≤ 0,5 und e ≤ h1 für Trägerhöhen h> 300 mm
a/h ≤ 0,7 und e ≤ h1 für Trägerhöhen h ≤ 300 mm
Bild 7. Oben ausgeklinkter bzw. abgeschrägter Träger
a) Rechtwinklige Ausklinkung
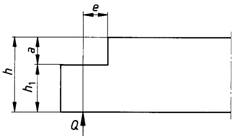
b) Abschrägung

8.2.2.2 Durchbrüche bei Biegeträgern aus Brettschichtholz
Durchbrüche im Sinne dieses Abschnittes sind Öffnungen in Brettschichtholzträgern mit den lichten Maßen d > 50 mm (siehe Bild 8). Durchbrüche sollen möglichst symmetrisch zur Trägerachse angeordnet werden; die Randabstände hro und hru müssen ≥ 0,3 h sein. Der Abstand lv vom Trägerende muss mindestens h, der Abstand lo von der Auflagermitte und von größeren Einzellasten mindestens h/2 betragen. Alle Ecken sind im Brettschichtholz mit einem Radius von mindestens 15 mm auszurunden.
Durchbrüche müssen, sofern ein genauerer Nachweis nicht geführt wird, verstärkt werden, wenn in Abhängigkeit von der auf den ungeschwächten Querschnitt in Durchbruchsmitte bezogenen Schubspannung τQ das größte lichte Maß d die Gleichung (16) oder Gleichung (17) erfüllt.
Bild 8: Maße und Anordnung von Durchbrüchen


lA ≥ h/2; lv und lz ≥ h; A ≤ h; hro und hru ≥ 0,3 h ; hd ≤ 0,4 h
| d > 100 - 42 τQ in mm | (16) |
| d > (0,1 - 0,042 τQ) * h | (17) |
Hierin bedeuten:
| τQ = | 1,5 Q | in MN/m2 | (18) |
| b * h |
| Q | Querkraft in Durchbruchsmitte; eine Abminderung nach Abschnitt 8.2.1.2 ist nicht zulässig |
| h | Höhe des Brettschichtholzträgers |
| b | Breite des Brettschichtholzträgers. |
Wenn von einem genaueren Nachweis verstärkter Durchbrüche abgesehen wird, darf eine Verstärkung durch aufgeleimtes Bau-Furniersperrholz nach DIN 68 705 Teil 5 der Klasse 100 nach Bild 9 erfolgen.
Die Gesamtverstärkungsdicke t (je Seite t/2) muss in Abhängigkeit von der in Durchbruchsmitte vorhandenen Schubspannung τQ in MN/m2 und der Trägerbreite b in mm
| t ≥ (0,15 + 0,4 * τQ) * b in mm | (19) |
betragen, jedoch mindestens 20 mm.
Weitere bei der Verstärkung von Durchbrüchen mittels Bau-Furniersperrholz zu beachtende Maße ergeben sich aus Bild 9. Die Faserrichtung des Deckfurniers muss parallel zur Faserrichtung der Trägerlamellen verlaufen. Für die Verleimung, die auch als Nagelpressleimung erfolgen darf, ist Resorcinharzleim zu verwenden. Im Übrigen gilt Abschnitt 12.5.
8.2.3 Gekrümmte Träger und Satteldachträger aus Brettschichtholz
8.2.3.1 Allgemeines
Für gekrümmte Träger und Satteldachträger aus Brettschichtholz nach den Bildern 10 bis 12 sind im gekrümmten Bereich bzw. im Firstquerschnitt Quer- und Längsspannungen, außerdem bei Satteldachträgern nach den Bildern 11 und 12 Spannungskombinationen nachzuweisen.
Für Träger mit Rechteckquerschnitt dürfen die maximalen Quer- und Längsspannungen infolge Moment im gekrümmten Bereich bei Trägerformen nach Bild 10 bzw. im Firstquerschnitt bei Trägerformen nach den Bildern 11 und 12 für γ ≤ 20° nach den Abschnitten 8.2.3.2 und 8.2.3.3 berechnet werden, sofern ein genauerer Nachweis nicht geführt wird.
Für den Nachweis der Spannungskombination nach Abschnitt 8.2.3.4 ist die größte außerhalb des Firstbereiches auftretende Längsspannung zu berücksichtigen.
Bild 9. Maße und Anordnung der Verstärkungen

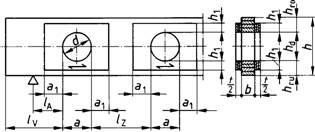
lA ≥ h/2 ; lv und lz ≥ h; a ≤ h;
a1 ≥ 0,25a und ≥ h1 ; hro und hru ≥ 0,3 h;
hd ≤ 0,4 h ; h1 ≥ 0,25 hd und ≥ 0,1 h ; b ≤ 220 mm
8.2.3.2 Querspannungen
Die Querspannung Ãn ist mit
max o = χq * M / Wm = χq * M / Wm | (20) |
zu bestimmen.
Dabei ist
| χq = Aq + Bq * [hm / rm] + Cq * [hm / rm]2 | (21) |
mit
| Aq = 0,2 * tan γ | (22) |
| Bq = 0,25 - 1,5 * tan γ + 2,6 * tan2 γ | (23) |
| Cq = 2,1 *tan γ - 4 * tan2 γ | (24) |
Die nach Gleichung (20) ermittelten Querspannungen dürfen die Werte in Tabelle 5, Zeilen 3 bzw. 5a, nicht überschreiten.
Bild 10. Gekrümmter Träger mit konstanter Trägerhöhe

Bild 11. Satteldachträger mit gekrümmtem Untergurt
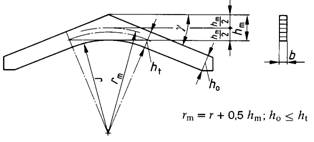
Bild 12. Satteldachträger mit geradem Untergurt
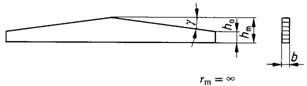
8.2.3.3 Längsspannungen am inneren bzw. am unteren Trägerrand
Die Längsspannung o|| ist mit
| max σ|| = xl * M / Wm | (25) |
zu bestimmen.
Dabei ist
| χl = Αl + Bl * [hm / rm] + Cl * [hm / rm)2 + Dl * [hm / rm]3 | (26) |
mit
| Αl = 1 + 1,4 * tan γ + 5,4 * tan2 γ | (27) |
| Bl = 0,35 - 8 * tan γ | (28) |
| Cl = 0,6 + 8,3 * tan γ - 7,8 * tan2 γ | (29) |
| Dl = 6 * tan2 γ | (30) |
Die Längsspannungen am äußeren bzw. oberen Trägerrand dürfen mit χ1 = 1,0 berechnet werden.
Die nach Gleichung (25) ermittelten Längsspannungen dürfen die Werte in Tabelle 5, Zeile 1, nicht überschreiten.
8.2.3.4 Spannungskombination
Verläuft bei Brettschichtholzträgern die Faserrichtung nicht parallel zum Trägerrand, so dass hier zusätzlich zu den Längsspannungen Ã' noch Querspannungen Ãn und Schubspannungen r auftreten (siehe Bild 13), so ist für den Biegezugrand
[σ|| / zul σB]2 + [oZ / 1,25 zul σZ / 1,25 zul σZ ]2 + [τ / 1,33 zul τa]2 ≤ 1 ]2 + [τ / 1,33 zul τa]2 ≤ 1 | (31) |
für den Biegedruckrand
[σ|| / zul σB]2 + [σD / zul σD / zul σD ]2 + [τ / 2,66 zul τa]2 ≤ 1 ]2 + [τ / 2,66 zul τa]2 ≤ 1 | (32) |
einzuhalten. Hierin sind im Nenner die entsprechenden zulässigen Spannungen für Brettschichtholz der Güteklasse I nach Tabelle 5 einzusetzen. Bei schrägen druckbeanspruchten Rändern darf auf die Berücksichtigung der Spannungskombination verzichtet werden, wenn α ≤ 3° ist.
Bild 13. Längs-, Quer- und Schubspannungen an einem dreiecksförmigen Element des Biegedruckrandes
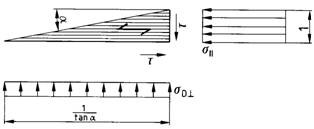
| τ | = o|| * tan α |
oD | = o|| * tan2 α |
| α | = Winkel zwischen dem Trägerrand und der Faserrichtung |
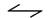 | Faserrichtung |
8.2.4 Kopfbandbalken
Soweit Pfetten und Balken mit Kopfbändern in allen Feldern eine vorwiegend gleichmäßig verteilte Last oder gleiche, in kleineren Abständen stehende Einzellasten (Sparren) aufzunehmen haben, und benachbarte Stützenabstände l (siehe Bild 14) nicht um mehr als 1/5 voneinander abweichen, darf die größte Feldweite (l1, l2, l3 oder l4) in Rechnung gestellt werden. Für diese Feldweite ist das Bauteil als ein frei drehbar gelagerter Träger auf zwei Stützen zu berechnen. Bei Bauteilen mit feldweise auftretenden Verkehrslasten sowie bei ungleichen Stützenabständen l, die um mehr als 1/5 vom kleinsten Stützenabstand abweichen, ist eine genauere Berechnung auch der Stützen durchzuführen und die Ausführung entsprechend zu gestalten.
Bild 14. Feldweiten bei Kopfbandbalken

Bei Pfetten und Balken mit Sattelhölzern ohne Kopfbänder ist als Stützweite stets der Achsabstand der Unterstützungen in Rechnung zu stellen.
8.3 Biegeträger aus nachgiebig miteinander verbundenen Querschnittsteilen
8.3.1 Bei der Spannungsberechnung zusammengesetzter Biegeträger muss die Nachgiebigkeit der Verbindungsmittel gegebenenfalls berücksichtigt werden.
Für Träger mit einfach-symmetrischem Querschnitt nach Typ 5 (siehe Tabelle 8 sowie Bild 15d) sind die Spannungen wie folgt zu berechnen:
| σsi = ± M / ef I * γi * ai * Ai / Ain * ni | (33) |
| σri = ± M / ef I * (γi * ai * Ai / Ain + hi/2 * Ii * Iin)* ni | (34) |
Hierin bedeuten:
| M | Biegemoment, positiv bei Druckbeanspruchung der oberen und Zugbeanspruchung der unteren Randfaser des Trägers |
| σsi σri | Schwerpunktsspannungen bzw. Randspannungen in den einzelnen Querschnittsteilen (Gurte bzw. Steg), die Vorzeichen gehen aus Bild 15d hervor |
| ai | Abstände der Schwerachsen der ungeschwächten Querschnittsflächen von der maßgebenden Spannungsnullebene y-y, es wird a2 ≥ 0 und ≤ h2/2 vorausgesetzt |
| hi | Dicken bzw. Höhen der einzelnen Querschnittsteile |
| γi | Abminderungswerte zur Berechnung von ef I nach Gleichung (36) bzw. Gleichung (37) |
| Ii Iin | Flächenmomente 2. Grades der ungeschwächten bzw. geschwächten Querschnittsteile (Ii = bi * hi 3/12) |
| ef I | Wirksames Flächenmoment 2. Grades des ungeschwächten Querschnittes nach Gleichung (35) |
| Ai Ain | Querschnittsflächen der ungeschwächten bzw. geschwächten Querschnittsteile (Ai = bi * hi) |
| bi | Querschnittsbreiten |
| Ei | Elastizitätsmoduln der einzelnen Querschnittsteile |
| Ev | beliebiger Vergleichs-Elastizitätsmodul |
| ni | = Ei/Ev. |
Bild 15. Verschiedene Querschnittstypen zusammengesetzter Biegeträger und Spannungsverteilung (schematisch) bei positivem Biegemoment
a) Typ 1

b) Typ 3
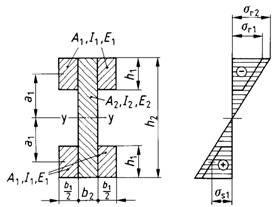
c) Typ 4

d) Tvp 5

Tabelle B. Querschnittstypen und Rechenwerte für Verschiebungsmoduln C in N/mm
| Für Biegung bzw. Knickung maßgebende Schwerachse | Verbindungsmittel | Typ 1 | Typ 2 | Typ 3 | Typ 4 | Typ 5 |
 |  | 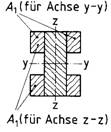 |  |  | ||
| Y - Y | Nagel (durch eine Fuge) | 600 | 600 | 900 | 600 | 600 |
| Nagel (durch zwei Fugen) | 700 | 700 | 900 je Fuge | - | 700 | |
| z-z | Nagel (durch eine Fuge) | - | 900 | 600 | - | - |
| Nagel (durch zwei Fugen) | - | 900 je Fuge | 700 | - | ||
| Y - Y und z - z | Dübel nach DIN 1052 Teil 2 | 15000 für zulässige Belastung l) bis 16 kN | ||||
| 22500 für zulässige Belastung l) über 16 bis 30 kN | ||||||
| 30000 für zulässige Belastung 1) über 30 kN | ||||||
| y - y z- z | Stabdübel, Passbolzen | 0,7 * zul N je Fuge mit zul N = zulässige Belastung g in N je Anschlußfuge2) | ||||
| 1) Als zulässige Belastung sind die Werte je Dübel für den Lastfall H (siehe DIN 1052 Teil 2, Tabellen 4, 6 und 7) maßgebend.
2) Für Laubholz, Holzartgruppe C: 1,0 * zul N. | ||||||
Flächenmomente 2. Grades geschwächter Querschnittsteile dürfen auf die Schwerachsen der ungeschwächten Querschnittsteile bezogen werden.
Unter Beachtung von Abschnitt 8.2.1.1 dürfen die Randspannungen ori die zulässigen Werte für Biegung nach Tabelle 5, Zeile 1, und die Schwerpunktsspannungen osi in den gezogenen Querschnittsteilen die zulässigen Werte für Zug nach Tabelle 5, Zeile 2, nicht überschreiten. Außerdem ist Abschnitt 5.1.7 zu beachten.
Das wirksame Flächenmoment 2. Grades ef I des ungeschwächten Querschnittes ist mit
 | (35) |
mit
| γ1,3 = 1 / 1 + k1,3 | (36) |
| γ2 = 1 | (37) |
und
| k1,3 = π2 * E1,3 * A1,3 * e'1,3 / l2 * C1,3 | (38) |
sowie
 | (39) |
der Berechnung zugrunde zu legen.
Hierin bedeuten insbesondere:
| e'1, e'3 | mittlere Abstände der in eine Reihe geschobenen Verbindungsmittel (siehe Bild 16), mit denen die Gurte an den Steg angeschlossen sind |
| C1 C3 | Verschiebungsmoduln der Verbindungsmittel, mit denen die Gurte an den Steg angeschlossen sind, nach Tabelle 8 |
| l | maßgebende Stützweite. |
Bild 16. Maßgebender Abstand e'1,3 bei mehrreihiger Anordnung der Verbindungsmittel

Bei der Berechnung der k-Werte nach Gleichung (38) sind für den Elastizitätsmodul und den Verschiebungsmodul Abminderungen nach Abschnitt 4.1.2 nicht zu berücksichtigen. Für Holzschrauben nach DIN 96, DIN 97 und DIN 571 und für Klammern nach DIN 1052 Teil 2 dürfen als Verschiebungsmoduln die Werte für Nägel nach Tabelle 8 angenommen werden.
Für Träger mit doppeltsymmetrischen Querschnitten nach Typ 1 bis Typ 3 (siehe Tabelle 8 sowie Bild 15a und Bild 15b) ist Α3 = Α1, E3 = E1, n3 = n1, e'1= e'3= e' und C1 = C3 = C. Damit erhält man nach Gleichung (38) bzw. Gleichung (36) k1 = k3 = k bzw. γ1 = γ 3= γ, ferner nach Gleichung (39) a2 = 0. Nunmehr ergeben sich die Spannungen nach Gleichung (33) zu os1 = os3, os2 = 0, ferner nach Gleichung (34) σr1 = σr3.
Für Träger mit einfach-symmetrischem Querschnitt nach Typ 4 (siehe Tabelle 8 und Bild 15c) dürfen die Gleichungen (38) und (39) mit Α3 = 0 zugrunde gelegt werden. Die Spannungen ergeben sich sinngemäß aus den Gleichungen (33) und (34).
8.3.2 Bei Durchlaufträgern muss, wenn keine genauere Berechnung durchgeführt wird, bei der Ermittlung von k mit 4/5 der Stützweite l des betreffenden Feldes gerechnet werden, wobei für den Spannungsnachweis über den Zwischenstützen jeweils der kleinere Wert der beiden anschließenden Felder einzuführen ist.
Bei Kragträgern ist mit l = 2 * lK zu rechnen; mit lK als Kraglänge.
8.3.3 Die Verbindungsmittel sind unter Berücksichtigung des wirksamen Flächenmomentes 2. Grades ef I nach Gleichung (35) in der Regel für die größte Querkraft max Q zu berechnen.
Für Träger mit einfach-symmetrischem Querschnitt nach Typ 5 berechnen sich die größten Schubflüsse ef t1,3 in den Anschlussfugen der Gurte zu
| ef t1,3 = max Q / ef I * γ1,3 * n1,3 * S1,3 | (40) |
und die erforderlichen Abstände e'1,3 der Verbindungsmittel zu
| erf e'1,3 = zul N1,3 / ef t1,3 | (41) |
Die Verbindungsmittel sind in der Regel unabhängig vom Verlauf der Querkraftlinie gleichmäßig über die Trägerlänge anzuordnen.
Werden die Verbindungsmittelabstände entsprechend der Querkraftlinie abgestuft und sind die maximalen Abstände max e'1,3
höchstens 4 * min e'1,3, so darf für e'1,3 der jeweilige Verbindungsmittelabstand
| `e'1,3 = 0,75 * min e`1,3 + 0,25 * max e'1,3 | (42) |
in Gleichung (38) eingesetzt werden.
Die Schubspannungen in neutralen Fasern sind für max Q ebenfalls unter Berücksichtigung von ef I nachzuweisen.
Für Träger nach Typ 5 ergibt sich die größte Schubspannung in der maßgebenden Spannungsnullebene y-y zu

In den Gleichungen (40) bis (43) bedeuten insbesondere:
| S1 S3 | Flächenmomente 1. Grades der Gurte, bezogen auf die maßgebende Spannungsnullebene y-y (S1,3 = b1,3 * h1,3 * α1,3 |
| S2 | Flächenmoment 1. Grades der oberhalb der maßgebenden Spannungsnullebene y-y liegenden Stegfläche, bezogen auf die Spannungsnullebene y- y (S2 = b2 * (h2/2 - a2)2 / 2) |
| zul N1 zul N3 | zulässige Belastungen des verwendeten Verbindungsmittels. |
Bei Trägern mit doppeltsymmetrischen Querschnitten nach Typ 1 bis Typ 3 (siehe Tabelle 8 sowie Bild 15a und Bild 15b) und ebenso bei Trägern mit einfach-symmetrischem Querschnitt nach Typ 4 (siehe Tabelle 8 und Bild 15c) sind die Gleichungen (40) bis (43) sinngemäß anzuwenden, siehe auch Abschnitt 8.3.1.
Ist bei Trägern nach Typ 2 und Typ 3 (siehe Tabelle 8) die Schwerachse z-z maßgebend, so ist ebenfalls sinngemäß zu verfahren.
8.3.4 Der Durchbiegungsnachweis nach Abschnitt 8.5 ist mit ef I nach Gleichung (35) und Ev zu führen. Dabei darf der jeweils größere Verschiebungsmodul C, der sich aus den 1,25fachen Werten nach Tabelle 8 oder aus den Werten nach DIN 1052 Teil 2, Tabelle 13, ergibt, in Gleichung (38) eingesetzt werden.
8.4 Vollwand- und Fachwerkträger
8.4.1 Vollwandträger mit Plattenstegen
Vollwandträger nach Bild 17, deren Stege aus Bau-Furniersperrholz oder Flachpressplatten bestehen und ungestoßen oder mit verleimten Stößen hergestellt werden, müssen unter Berücksichtigung der verschiedenen Elastizitätsmoduln der Steg- und Gurtwerkstoffe berechnet werden. Bei genagelten Stößen ist deren Nachgiebigkeit erforderlichenfalls zu berücksichtigen.
Bei nachgiebigem Anschluss der Gurte an den Steg muss der Träger nach Abschnitt 8.3 berechnet werden.
Sofern kein genauerer Beulnachweis geführt wird, ist bei annähernd gleichmäßig belasteten verleimten Vollwandträgern mit Plattenstegen (siehe Bild 17) aus Bau-Furniersperrholz aus mindestens fünf Lagen nach DIN 68 705 Teil 3 oder Teil 5
| hSl / bS ≤ 35 | (44) |
Und aus Flachpressplatten nach DIN 86763
| hSl / bS ≤ 50 | (45) |
einzuhalten.
Bei genagelten Vollwandträgern mit Plattenstegen ist in den Gleichungen (44) und (45) hSl durch hSg zu ersetzen.
Bild 17: Vollwandträger mit Plattenstegen
a) I-Querschnitt
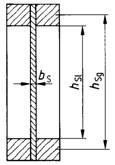
b) Kasten-Querschnitt
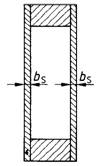
Hierin bedeuten:
| hSi | lichte Höhe der Plattenstege |
| hSg | Mittenabstand der Gurtquerschnittsflächen |
| bS | Dicke der Plattenstege. |
Mindestens im Auflager- und im Einleitungsbereich von Einzellasten sind Aussteifungen erforderlich. Bei Trägerhöhen über 500 mm sollte der Steifenabstand die 3fache Trägerhöhe nicht überschreiten.
8.4.2 Vollwandträger mit Bretterstegen
8.4.2.1 Bei verbretterten I-Trägern, Kastenträgern oder I-Kastenträgern mit vernagelten, gekreuzten Brettlagen ist der Steg bei der Bestimmung des wirksamen Flächenmomentes 2. Grades nicht zu berücksichtigen. Die Stegbretter und deren Anschlüsse an den Gurten müssen für die Aufnahme der Querkräfte bemessen werden. Der Spannungsnachweis in den Gurten ist unter Berücksichtigung der Nachgiebigkeit der Verbindungsmittel zu führen. Bei abgestuftem Verbindungsmittelabstand darf Gleichung (41) sinngemäß angewendet werden.
Die Knicksicherheit der auf Druck beanspruchten Stegbretter muss ebenfalls nachgewiesen werden, soweit diese nicht mit den Zugbrettern ausreichend verbunden sind. Die Aufnahme der beim Kastenquerschnitt mit kreuzweiser Verbretterung aus den Brettkräften entstehenden Drillmomente ist nachzuweisen.
8.4.2.2 Wird der I-Träger mit kreuzweiser Verbretterung in zwei getrennten Hälften (einschnittig) hergestellt, so muss die Aufnahme der zwischen den beiden Trägerhälften auftretenden Kopplungskräfte nachgewiesen werden.
8.4.2.3 Für die Aufnahme von zusätzlichen Druck- oder Zugkräften (z.B. bei Rahmen) dürfen verbretterte Stege von Vollwandträgern nicht in Rechnung gestellt werden.
8.4.2.4 Bestehen die Gurte aus mehreren Einzelteilen (siehe Bild 18), so sind, falls kein genauerer Nachweis geführt wird, die Querschnitte der Einzelteile mit folgenden Beiwerten ζ in Rechnung zu stellen:
Bild 18. Zusammengesetzter Gurtquerschnitt eines genagelten Vollwandträgers

Mehr als zwei aufeinander liegende Einzelteile sind nicht zu verwenden; bei Gurten aus zusammengeleimten Einzelteilen (Brettschichtholz) ist die Anzahl der Einzelteile nicht beschränkt und eine Abminderung innerhalb der Gurtteile nicht erforderlich.
8.4.3 Fachwerkträger
Bei parallelgurtigen oder trapezförmigen Fachwerkträgern mit nachgiebigen Stabanschlüssen sind die Biegespannungen in den Gurten nachzuweisen, wenn die Gurthöhe mehr als 1/7 der Trägerhöhe beträgt.
8.5 Durchbiegungen und Überhöhungen
8.5.1 Um insbesondere die Gebrauchsfähigkeit der Konstruktion und der Bauteile zu sichern, sind Grenzwerte für die Durchbiegungen aus Verkehrslasten (einschließlich Wind- und Schneelast; ohne Schwing- und Stoßbeiwert) und aus Gesamtlast (ständige Last und Verkehrslasten einschließlich Wind- und Schneelast; ohne Schwing- und Stoßbeiwert) einzuhalten.
Wenn Bauart und Nutzung eines Bauwerkes es erfordern, können auch geringere als in Tabelle 9 oder in Abschnitt 8.5.7 und Abschnitt 8.5.8 angegebene zulässige Durchbiegungen maßgebend werden.
8.5.2 Bei der Berechnung der Durchbiegung darf der ungeschwächte Querschnitt eingesetzt werden. Bei zusammengesetzten Trägern ist der Nachweis nach Abschnitt 8.3.4 zu führen.
8.5.3 Für die rechnerisch zulässigen Durchbiegungen von Brettschichtholzträgern, zusammengesetzten Trägern, Vollwandträgern sowie von Fachwerkträgern gelten die in Tabelle 9 angegebenen Werte. Für Aussteifungskonstruktionen siehe Abschnitt 10.
Bei der Durchbiegungsermittlung von Fachwerkträgern ist zu unterscheiden zwischen einer Näherungsberechnung, bei der nur die elastische Verformung der Gurtstäbe berücksichtigt wird, und einer genaueren Berechnung, bei der die elastische Verformung sämtlicher Stäbe und die Nachgiebigkeit aller Anschlüsse und Stöße zu berücksichtigen sind. Dies gilt auch für einsinnig verbretterte Vollwandträger. Bei Flachdächern mit Spannweitenverhältnissen l/h > 10 ist in der Regel die genauere Berechnung durchzuführen.
8.5.4 Bei Trägern mit Vollholz- oder Plattenstegen ist der Durchsenkungsanteil aus der Schubverformung zu berücksichtigen.
Bei Vollwandträgern genügt es dabei im allgemeinen, wenn kein genauerer Nachweis geführt wird, die rechnerische Durchsenkung aus der Schubverformung näherungsweise unter Annahme einer stellvertretenden, gleichmäßig verteilten Last zu ermitteln.
Für Vollwandträger auf zwei Stützen mit gleichbleibendem Querschnitt darf diese Durchsenkung in Balkenmitte zu
| max fτ = | q * l2 | (46) |
| 8 G * ΑSteg |
angenommen werden; mit G als Schubmodul des Stegmaterials.
Bei Durchlaufträgern darf der Anteil max fτ in gleicher Weise berechnet werden; wobei für l die gesamte Feldweite des betrachteten Feldes einzusetzen ist.
8.5.5 Bei Brettschichtholzträgern, zusammengesetzten Biegebauteilen und bei Fachwerkträgern ist in der Regel das Gesamtsystem parabelförmig zu überhöhen. Die Überhöhung soll mindestens der rechnerischen Durchbiegung aus Gesamtlast unter Berücksichtigung der Kriechverformungen entsprechen. Bei Konstruktionen mit nachgiebigen Verbindungsmitteln soll der Einfluss der Nachgiebigkeit berücksichtigt werden. Ohne Berechnung der Überhöhung muss mindestens um l/300, bei Verwendung von halbtrockenem oder frischem Holz mindestens um l/200, bei Kragträgern um l/150 überhöht werden. Bei Rahmen ist sinngemäß zu verfahren.
8.5.6 Bei auskragenden Bauteilen darf die rechnerische Durchbiegung der Kragenden die Werte in Tabelle 9, bezogen auf die Kraglänge, um 100 % überschreiten.
8.5.7 Bei Decken unter und über Wohn-, Büro- und ähnlichen Räumen sowie unter Fabrik- und Werkstatträumen darf die rechnerische Durchbiegung unter der Gesamtlast im allgemeinen höchstens l/300 betragen. Dies gilt in der Regel auch für Pfetten, Sparren und Balken im Bereich des oberen Raumabschlusses von Wohn-, Büro- und ähnlichen Räumen.
8.5.8 Bei Pfetten und Sparren, ferner bei Balken von Stalldecken, Scheunen und dergleichen sowie im landwirtschaftlichen Bauwesen auch bei Vollwand- und Fachwerkträgern ohne Überhöhung darf die rechnerische Durchbiegung unter der Gesamtlast l/200 betragen. Bei der Näherungsberechnung von Fachwerkträgern muss der Wert l/400 eingehalten werden.
8.5.9 Bei Stützen und Riegeln in den Außenwänden geschlossener Gebäude darf die rechnerische Durchbiegung unter horizontaler Last, z.B. unter Windlast nach DIN 1055 Teil 4, in der Regel nicht mehr als 1/200 der Stützweite betragen.
8.5.10 Die rechnerische Durchbiegung von Dach- und unmittelbar belasteten Deckenschalungen sowie von oberen Dach- und Deckenbeplankungen unter Gesamtlast darf höchstens l/200, jedoch nicht mehr als 10 mm, unter Eigenlast und Einzellast von 1 kN (Mannlast) höchstens l/100, jedoch nicht mehr als 20 mm betragen. Dabei darf der Durchbiegungsanteil aus der Schubverformung vernachlässigt werden. Bei Aussteifungsscheiben aus Holzwerkstoffen ist Abschnitt 10.3.1 zu beachten.
8.6 Stabilisierung biegebeanspruchter Bauteile
8.6.1 Biegebeanspruchte Bauteile müssen gegen seitliches Ausweichen gesichert sein.
Sind Träger mit Rechteckquerschnitt der Höhe h und der Breite b im Abstand s seitlich praktisch unverschieblich festgehalten, so darf für die Biegespannung aus einem in diesem Bereich konstant angenommenen Biegemoment M der Nachweis
| M/W / kB * 1,1 * zul σB ≤ 1 | (47) |
geführt werden, wobei für kB einzusetzen ist:
| kB = |  | 1 | für | λB ≤ 0,75 | (48) |
| 1,56 - 0,75 * λB | für 0,75 ≤ | λB ≤ 1,4 | (49) | ||
| 1 / λ2B | für | λB ≤ 1,4 | (50) |
Dabei ist λB der Kippschlankheitsgrad.

Als Lasterhöhungsbeiwert ist für beide Lastfälle H und HZ γ1 = 2,0 einzusetzen.
Ist bei Vollwandträgern mit I- oder Kastenquerschnitt der Druckgurt in einzelnen Punkten, deren Abstand s beträgt, seitlich praktisch unverschieblich festgehalten und der auf die maßgebende Schwerachse des Trägers bezogene Trägheitsradius i des Gurtquerschnittes größer als s/40, so darf ein weiterer Nachweis entfallen.
Ist i < s/40, so darf, sofern kein genauerer Nachweis geführt wird, die Schwerpunktsspannung des gedrückten Querschnittsteiles den Wert kS * zul ok nicht überschreiten. Dabei ist zul ok nach Gleichung (59) zu ermitteln, wobei ω die dem Schlankheitsgrad λ = s/i zugeordnete Knickzahl nach Tabelle 10 ist. Für kS ist die zum Schlankheitsgrad λ = 40 zugehörige Knickzahl ω nach Tabelle 10 einzusetzen. Gegebenenfalls ist ef I nach den Gleichungen (35) bis (39) zu bestimmen (siehe auch Abschnitt 9.3.3.2).
Tabelle 9. Zulässige Durchbiegungen von biegebeanspruchten Trägern
| Last | Ausführung mit Überhöhung nach Abschnitt 8.5.5 | Ausführung ohne Überhöhung | ||||
| BSH- Träger, zusammengesetzte Träger, Vollwandträger | Fachwerkträger1) | BSH- Träger, zusammengesetzte Träger, Vollwandträger | Fachwerkträger1) | |||
| Näherungsberechnung | genauere Berechnung | Näherungsberechnung | genauere Berechnung | |||
| Verkehrslast | l/300 | l/600 | l/300 | - | - | - |
| Gesamtlast | l/200 | l/400 | l/200 | l/300 | l/600 | l/300 |
| 1 )Einschließlich einsinnig verbretterter Vollwandträger. | ||||||
8.6.2 Anstelle des Nachweises nach Abschnitt 8.6.1 darf auch der Tragsicherheitsnachweis nach der Spannungstheorie II. Ordnung geführt werden. Die Nachgiebigkeit der Verbindungsmittel sowie die Kriechverformungen sind gegebenenfalls zu berücksichtigen.
Die Schnittgrößen sind für die γ1-fachen Lasten zu ermitteln. Der Nachweis ausreichender Tragsicherheit ist erbracht, wenn an keiner Stelle des Biegeträgers die γ1-fachen zulässigen Spannungen und die γ1-fachen zulässigen Belastungen der Verbindungsmittel überschritten werden.
Bei im Grundriss planmäßig geraden Biegeträgern ist rechnerisch eine seitliche wahlweise sinus- oder parabelförmige Vorkrümmung der Stabachse zu berücksichtigen. Hierbei ist in Stabmitte eine rechnerische seitliche Ausmitte nach Gleichung (73) anzunehmen, wobei für s der Abstand der Kippaussteifungen einzusetzen ist. Zu den übrigen Bezeichnungen siehe Abschnitt 9.6.3.
In diesem Falle darf die Querschnittseckspannung aus nicht planmäßiger Doppelbiegung die zulässige Biegespannung nach Tabelle 5, Zeile 1, um 10 % überschreiten. Der Nachweis für die einfache Biegung ist zusätzlich zu führen.
9 Bemessungsregeln für Druckstäbe
9.1 Knicklängen
9.1.1 Ist der Druckstab an den Enden durch abstützende Bauteile (wie Verbände, Scheiben oder dergleichen) gegen seitliches Ausweichen gesichert, so ist eine gelenkige Lagerung beider Stabenden anzunehmen. Ist der Druckstab in Zwischenpunkten gegen festliegende andere Punkte abgestützt, darf als Knicklänge für das Ausknicken in der Richtung, in der die Abstützung wirksam ist, der Abstand der Abstützung in Rechnung gestellt werden. Sind diese Voraussetzungen nicht erfüllt, so sind entsprechend größere Knicklängen in Rechnung zu stellen. Für Druckgurte von Vollwandträgern siehe auch Abschnitt 8.6.
9.1.2 Als Knicklänge der Gurtstäbe von Fachwerken ist für das Knicken in der Fachwerkebene in der Regel die Länge der Netzlinie einzusetzen. Bei Füllstäben darf mit sk = 0,8 * s gerechnet werden; mit s als Länge ihrer Netzlinie. Ist ein Füllstab jedoch nur mittels Versatz oder durch Dübel mit einem Bolzen oder nur durch Bolzen angeschlossen, so gilt sk = s.
Für das Knicken aus der Fachwerkebene ist als Knicklänge bei Gurtstäben der Abstand der Queraussteifungen und bei Füllstäben stets die Länge der Netzlinie einzusetzen.
Hierzu siehe auch Abschnitt 10.5.
9.1.3 Die Knicklänge der Sparren von Kehlbalkenbindern darf für das Knicken in der Systemebene näherungsweise, wenn kein genauerer Nachweis geführt wird, bei verschieblichem Kehlbalken zu sk = 0,8 * s angenommen werden, wenn die Länge su des unteren Sparrenabschnittes kleiner als 0,7 * s, aber größer als 0,3 * s ist; hierin ist s die gesamte Sparrenlänge. Andernfalls ist mit sk = s zu rechnen. Bei unverschieblichem Kehlbalken darf die Knicklänge mit sk = s bzw. so angenommen werden. Dabei ist der Nachweis mit der jeweils größten Druckkraft im unteren bzw. oberen Sparrenabschnitt zu führen.
Für das Knicken aus der Systemebene ist der Abstand der Queraussteifungen maßgebend.
Hierzu siehe Abschnitt 10.5.
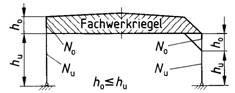
9.1.4 Bei Stützen von Rahmen mit Fachwerkriegeln nach Bild 19 ist näherungsweise, wenn kein genauerer Nachweis geführt wird, für Knicken in der Rahmenebene die Knicklänge mit
| sk = 2hu * (1 + 0,35 ho / hu) | (52) |
einzusetzen. Dabei ist der Nachweis so zu führen, als ob die größere der beiden Stabkräfte No und Nu über die gesamte Länge h = ho + hu auftreten würde.
Bild 19. Zweigelenkrahmen mit Fachwerkriegel
9.1.5 Für Drei- und Zweigelenkbogen nach Bild 20 mit einem Pfeilverhältnis f/l zwischen 0,15 und 0,5 und wenig veränderlichem Querschnitt darf, wenn kein genauerer Nachweis geführt wird, für das Ausknicken in der Bogenebene die Knicklänge mit
| sk = 1,25 * s | (53) |
eingesetzt werden; mit s als halbe Bogenlänge.
Hierbei ist für den Knicknachweis die Druckkraft im Viertelspunkt anzunehmen.
Bild 20. Bogensystem
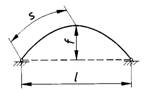
Bild 21. Rahmensystem

9.1.6 Bei symmetrischen Zwei- und Dreigelenkrahmen nach Bild 21 darf für das Knicken in der Binderebene, wenn kein genauerer Nachweis geführt wird, die Knicklänge des Stieles mit
| sk=2h * (1 + 0,4 c)0,5 | (54) |
angenommen werden.
Dabei ist
| c = I * 2s / Io* h | (55) |
Hierin bedeuten:
| I | Flächenmoment 2. Grades des Stieles |
| Io | Flächenmoment 2. Grades des Riegels |
| h | Stielhöhe |
| s | Riegellänge. |
Die Knicklänge des Riegels darf, sofern kein genauerer Nachweis geführt wird, mit
| sk = 2h * (1+0,4c)0,5 * kR0,5 | (56) |
angenommen werden.
Dabei ist
| kR = Io * N / I * No | (57) |
Hierin bedeuten:
| N | mittlere Stabkraft des Stieles |
| No | mittlere Stabkraft des Riegels. |
Sind die Flächenmomente 2. Grades veränderlich, so darf mit den in 0,65 * h bzw. 0,65 * s vorhandenen Flächenmomenten 2. Grades gerechnet werden, aus denen auch die Trägheitsradien i mit den dort vorhandenen Querschnittsflächen zu ermitteln sind.
Beim Stabilitätsnachweis nach Gleichung (72) sind jeweils die im betrachteten Rahmenteil auftretenden Werte max N und max M einzusetzen.
9.1.7 Der Einfluss der Nachgiebigkeit der Verbindungen auf die Knicklänge ist erforderlichenfalls zu berücksichtigen.
9.1.8 Bei Fachwerkrahmen ist für das Knicken aus der Rahmenebene für die inneren gedrückten Stäbe der Rahmenstiele als Knicklänge der Abstand zwischen dem Fußpunkt und der Unterkante der Dachhaut anzunehmen, wenn der innere Rahmeneckpunkt seitlich nicht gehalten ist. Dabei ist zusätzlich eine Seitenkraft von 1/100 der größten, im inneren Rahmeneckpunkt einlaufenden Stabkraft an dieser Stelle zu berücksichtigen.
9.2 Schlankheitsgrad
Bei einteiligen Druckstäben sind Schlankheitsgrade bis λ = 150 zulässig, bei zusammengesetzten nicht verleimten Druckstäben bis ef λ = 175, bei Verbandsstäben sowie bei Zugstäben, die nur aus Zusatzlasten geringfügige Druckkräfte erhalten, bis λ = 200.
Bei Fliegenden Bauten (siehe DIN 4112) sind für Druckstäbe unter vorwiegend ruhender Beanspruchung Schlankheitsgrade bis λ = 200 zulässig. Zeltstangen zur Minderung des freien Durchhanges der Zeltplane dürfen Schlankheitsgrade bis λ = 250 haben.
9.3 Mittiger Druck
9.3.1 Allgemeines
Für planmäßig gerade, mittig gedrückte Stäbe ist der Knicknachweis nach den Abschnitten 9.3.2 bis 9.3.3.4 und, soweit Querschnittsschwächungen nach Abschnitt 6.4 nur im Bereich der Krafteinleitung vorhanden sind, der gewöhnliche Spannungsnachweis zu führen.
9.3.2 Knicknachweis für einteilige Stäbe
Bei einteiligen Stäben muss
| N / A | ≤ 1 | (58) |
| zul σk |
sein.
Hierbei ist
| zul σk = zul σD|| / ω | (59) |
Hierin bedeuten:
| N | größte im Stab auftretende Druckkraft |
| A | ungeschwächter Stabquerschnitt |
| zul σk | zulässige Druckspannung nach Tabelle 5, Zeile 4, bzw. Tabelle 6, Zeile 4, unter Berücksichtigung der Abschnitte 5.1.6, 5.1.7 und 5.1.9 bzw. 5.2.3 |
| ω | vom Schlankheitsgrad 2 abhängige Knickzahl nach Tabelle 10; Zwischenwerte dürfen geradlinig interpoliert werden |
| λ | maßgebender Schlankheitsgrad des Stabes, d. h. der größere der beiden Verhältniswerte ≫ y = sky / iy und ≫ Z = skZ / iz, dabei sind sky und skZ die Knicklängen des Stabes für das Ausknicken rechtwinklig zu den jeweiligen Schwerachsen (siehe Abschnitt 9.1) und iy bzw. iz, die zugehörigen Trägheitsradien. |
9.3.3 Knicknachweis für mehrteilige Stäbe
9.3.3.1 Allgemeines
Bei mehrteiligen Stäben muss zwischen nicht gespreizten (Querschnittstypen nach Tabelle 8) und gespreizten (Bauarten nach Bild 22) zusammengesetzten Stäben unterschieden werden (Spreizung = lichter Abstand A / Einzelstabdicke h1), ferner auch zwischen den Richtungen des Ausknickens (rechtwinklig zur y- bzw. z-Achse).
Bei nicht gespreizten Stäben mit Querschnitten nach Typ 1, Typ 4 und Typ 5 (siehe Tabelle 8) und bei gespreizten Stäben ist der mehrteilige Stab für das Ausknicken rechtwinklig zur Schwerachse z - z wie ein einteiliger Stab zu berechnen, dessen Flächenmoment 2. Grades Iz gleich der Summe der Flächenmomente 2. Grades der Einzelstäbe ist:
 | (60) |
Hierin ist IZ; das Flächenmoment 2. Grades des Einzelstabes, bezogen auf die Schwerachse z - z der Querschnittsfläche. Bestehen die Einzelstäbe aus unterschiedlichen Werkstoffen, gilt Abschnitt 9.3.3.2 sinngemäß.
Bei nicht gespreizten und bei gespreizten Stäben darf für das Ausknicken rechtwinklig zur Schwerachse y - y nicht in jedem Fall mit einem vollen Zusammenwirken der Einzelstäbe gerechnet werden. Der Knicknachweis ist dann mit dem wirksamen Schlankheitsgrad λ = λstarr zu führen.
Bei nicht gespreizten Stäben mit Querschnitten nach Typ 2 und Typ 3 (siehe Tabelle 8) gilt dies auch für das Ausknicken rechtwinklig zur Schwerachse z - z.
9.3.3.2 Zusammengesetzte, nicht gespreizte Stäbe mit kontinuierlicher Verbindung (Querschnittstypen nach Tabelle 8)
Bei verleimten Stäben darf λ = λstarr und I = Istarr gesetzt werden. Dabei ist Istarr sinngemäß mit den Gleichungen (35) und (39) mit γi = 1 zu berechnen.
Bei nachgiebigen Verbindungsmitteln ist ef I gegebenenfalls wie bei zusammengesetzten Biegeträgern nach den Gleichungen (35) bis (39) zu bestimmen, wobei anstelle der Stützweite l die maßgebende Knicklänge sk (siehe Abschnitt 9.1) einzuführen ist (C-Werte nach Abschnitt 8.3.1). Mit ef I wird der wirksame Schlankheitsgrad ef λ berechnet und die dem wirksamen Schlankheitsgrad ef λ zugehörige Knickzahl Tabelle 10 entnommen. Bei Verwendung unterschiedlicher Werkstoffe ist, sofern kein genauerer Nachweis geführt wird, die jeweils größte Knickzahl maßgebend.
Bei Stäben mit einfach-symmetrischem Querschnitt nach Typ 5 (siehe Tabelle 8) muss für alle Querschnittsteile
| N /`A * ni | ≤ 1 | (61) |
| zul ok |
sein mit
 | (62) |
Hierbei ist zul ok für den jeweiligen Querschnittsteil nach Gleichung (59) zu berechnen.
Bei Stäben mit Querschnitten nach Typ 1 bis Typ 4 (siehe Tabelle 8) ist sinngemäß zu verfahren.
Die Verbindungsmittel sind in der Regel für eine über die ganze Stablänge als wirksam angenommene Querkraft von
| Qi = ef ω * N / 60 | (63) |
zu bemessen.
Für ef λ < 60 darf dieser Wert mit dem Faktor ef λ / 60, jedoch höchstens mit 0,5 abgemindert werden.
Hierin bedeuten:
| ef ω | die dem wirksamen Schlankheitsgrad ef ≫ zugehÆrige Knickzahl nach Tabelle 10 |
| N | Druckkraft des Stabes. |
Tabelle 10. Knickzahlen ω
| Schlankheitsgrad | Vollholz aus Nadelhölzern nach Tabelle 1, Zeile 1 | Brettschichtholz aus Nadelhölzern nach Tabelle 1, Zeile 1 | Vollholz aus Laubhölzern nach Tabelle 1 | Bau-Furniersperrholz nach DIN 68 705 Teil 3 und Teil 5, Druckkraft parallel zur Faserrichtung der Deckfurniere | Flachpressplatten nach DIN 68 763 | |||||
| λ | Güteklasse | Güteklasse | Holzartgruppe | Lagenanzahl | Plattendicke mm | |||||
| I bis III | I | II | A | B | C | 3 | ≥ 5 | ≤ 25 | > 25 | |
| 0 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
| 10 | 1,04 | 1,00 | 1,00 | 1,04 | 1,03 | 1,03 | 1,02 | 1,01 | 1,03 | 1,02 |
| 20 | 1,08 | 1,00 | 1,00 | 1,08 | 1,08 | 1,07 | 1,05 | 1,04 | 1,07 | 1,07 |
| 30 | 1,15 | 1,00 | 1,00 | 1,15 | 1,15 | 1,15 | 1,11 | 1,12 | 1,15 | 1,16 |
| 40 | 1,26 | 1,03 | 1,03 | 1,25 | 1,27 | 1,29 | 1,22 | 1,28 | 1,28 | 1,34 |
| 50 | 1,42 | 1,13 | 1,11 | 1,40 | 1,45 | 1,50 | 1,38 | 1,54 | 1,49 | 1,61 |
| 60 | 1,62 | 1,28 | 1,25 | 1,59 | 1,69 | 1,79 | 1,61 | 1,91 | 1,78 | 1,99 |
| 70 | 1,88 | 1,51 | 1,45 | 1,83 | 2,00 | 2,17 | 1,92 | 2,53 | 2,15 | 2,48 |
| 80 | 2,20 | 1,92 | 1,75 | 2,13 | 2,38 | 2,67 | 2,30 | 3,30 | 2,60 | 3,24 |
| 90 | 2,58 | 2,43 | 2,22 | 2,48 | 2,87 | 3,38 | 2,87 | 4,18 | 3,22 | 4,10 |
| 100 | 3,00 | 3,00 | 2,74 | 2,88 | 3,55 | 4,17 | 3,55 | 5,16 | 3,98 | 5,07 |
| 110 | 3,63 | 3,63 | 3,32 | 3,43 | 4,29 | 5,05 | 4,29 | 6,24 | 4,82 | 6,13 |
| 120 | 4,32 | 4,32 | 3,95 | 4,09 | 5,11 | 6,01 | 5,11 | 7,43 | 5,73 | 7,30 |
| 130 | 5,07 | 5,07 | 4,63 | 4,79 | 5,99 | 7,05 | 5,99 | 8,72 | 6,73 | 8,56 |
| 140 | 5,88 | 5,88 | 5,37 | 5,56 | 6,95 | 8,18 | 6,95 | 10,11 | 7,80 | 9,93 |
| 150 | 6,75 | 6,75 | 6,17 | 6,38 | 7,98 | 9,39 | 7,98 | 11,61 | 8,96 | 11,40 |
| 160 | 7,68 | 7,68 | 7,02 | 7,26 | 9,08 | 10,68 | 9,08 | 13,20 | 10,19 | 12,97 |
| 170 | 8,67 | 8,67 | 7,92 | 8,20 | 10,25 | 12,06 | 10,25 | 14,91 | 11,50 | 14,64 |
| 175 | 9,19 | 9,19 | 8,39 | 8,69 | 10,86 | 12,78 | 10,86 | 15,80 | 12,19 | 15,52 |
| 180 | 9,72 | 9,72 | 8,88 | 9,19 | 11,49 | 13,52 | 11,49 | 16,71 | 12,90 | 16,41 |
| 190 | 10,83 | 10,83 | 9,89 | 10,24 | 12,80 | 15,06 | 12,80 | 18,62 | 14,37 | 18,29 |
| 200 | 12,00 | 12,00 | 10,96 | 11,35 | 14,18 | 16,69 | 14,18 | 20,63 | 15,92 | 20,26 |
| 210 | 13,23 | 13,23 | 12,08 | 12,51 | 15,64 | 18,40 | 15,64 | 22,75 | 17,55 | 22,34 |
| 220 | 14,52 | 14,52 | 13,26 | 13,73 | 17,16 | 20,19 | 17,16 | 24,97 | 19,27 | 24,52 |
| 230 | 15,87 | 15,87 | 14,50 | 15,01 | 18,76 | 22,07 | 18,76 | 27,29 | 21,06 | 26,80 |
| 240 | 17,28 | 17,28 | 15,78 | 16,34 | 20,43 | 24,03 | 20,43 | 29,71 | 22,93 | 29,18 |
| 250 | 18,75 | 18,75 | 17,13 | 17,73 | 22,16 | 26,08 | 22,16 | 32,24 | 24,88 | 31,66 |
Die Berechnung des Schubflusses ef t und des erforderlichen Abstandes e'1,3 der Verbindungsmittel erfolgt nach den Gleichungen (40) und (41).
9.3.3.3 Mehrteilige gespreizte Stäbe (Rahmen- und Gitterstäbe)
Für das Ausknicken rechtwinklig zur Schwerachse y - y ist bei Rahmenstäben nach Bild 22a bis Bild 22e der wirksame Schlankheitsgrad
| ef λ = (λ 2y + m/2 * c * λ21)0,5 | (64) |
zu berechnen.
Hierin bedeuten:
| λ = sky / iy | rechnerischer Schlankheitsgrad des Gesamtquerschnittes, der Trägheitsradius iy wird dabei aus dem vollen Flächenmoment 2. Grades iy,starr des Gesamtquerschnittes, bezogen auf die Schwerachse y - y, ermittelt |
| m | Anzahl der Einzelstäbe |
| c | Faktor je nach Ausbildung der Querverbindung nach Tabelle 11 |
| λ1 = s1 / i1 | Schlankheitsgrad des Einzelstabes für die zur Schwerachse y - y parallele Schwerachse. |
Als Knicklänge s1 des Einzelstabes ist der Mittenabstand der Querverbindungen zugrunde zu legen. λ 1 darf nicht größer als 60 und s1 höchstens 1/3 sky sein.
Für Achsabstände der Querverbindungen s1 < 30 * i1 ist beim Knicknachweis λ1 = 30 in Gleichung (64) einzusetzen.
Werden Zwischenhölzer nur mit Bolzen angeschlossen, so darf mit c = 3,0 gerechnet werden, wenn es sich um Bauteile für Fliegende Bauten nach DIN 4112 oder für Gerüste handelt. Dabei muss ein Nachziehen der Bolzen möglich sein. In allen anderen Fällen sind verbolzte mehrteilige Druckstäbe als aus nicht zusammenwirkenden Einzelstäben bestehend zu berechnen.
Bei großen Spreizungen sind Gitterstäbe nach Bild 22f und Bild 22g den Rahmenstäben mit Bindehölzern vorzuziehen.
Der wirksame Schlankheitsgrad ef λ ist hierfür nach Gleichung (64) zu ermitteln, wobei statt c * λ21 bei Vergitterung nach Bild 22f die Hilfsgröße
| (4π2 * E * A1) / (a1 * nD * CD * sin 2α) | (65) |
Bild 22. Bauarten von Rahmen- (A bis e) und Gitterstäben (f und g)
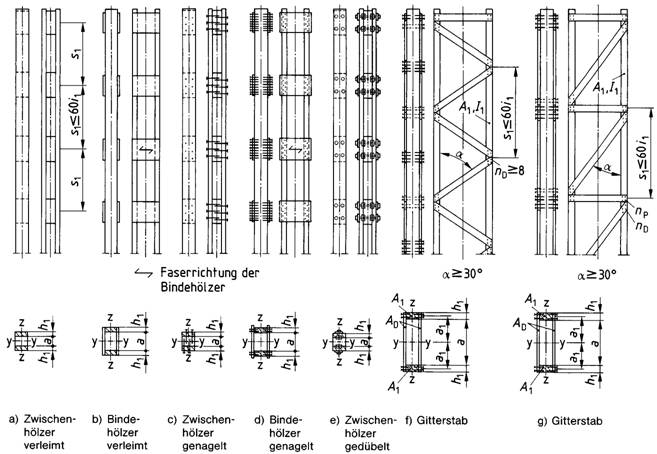
und bei Vergitterung nach Bild 22g die Hilfsgröße
| 4π2 * E * α1 | * | [ | 1 | + | sin 2 α | ] | (66) |
| a1 * sin 2 α | nD * CD | np * CP |
zu setzen ist. Hierin bedeuten:
| αl | Querschnitt des Einzelstabes |
| CD CP | Verschiebungsmodul der für den Anschluss der Streben bzw. Pfosten verwendeten Verbindungsmittel nach Tabelle 8 |
| α | Strebenneigungswinkel |
| nD np | Gesamtanzahl der Verbindungsmittel, mit denen die Gesamtstabkraft der Streben bzw. Pfosten angeschlossen ist. |
Tabelle 11. Faktor c für Rahmenstäbe nach Bild 22a bis Bild 22e
| Art der Querverbindung | Verbindungsmittel | Faktor c |
| Zwischenhölzer | Leim | 1,0 |
| Dübel | 2,5 | |
| Nägel, Holzschrauben, Klammern und Stabdübel | 3,0 | |
| Bindehölzer | Leim | 3,0 |
| Nägel, Holzschrauben und Klammern | 4,5 |
9.3.3.4 Bauliche Ausbildung und Berechnung der Querverbindungen
Alle Zwischen- und Bindehölzer, die Ausfachungen sowie ihre Anschlüsse sind für die in Abschnitt 9.3.3.2, Gleichung (63) angegebene Querkraft Qi zu bemessen.
Bei Rahmenstäben mit Zwischenhölzern nach den Bildern 22a, c und e, die in der Regel bei Spreizungen a/h1 ≤ 3 in Frage kommen, und bei Rahmenstäben mit Bindehölzern (siehe Bilder 22b und d) bei Spreizungen > 3 bis höchstens 6 entfällt auf eine solche Querverbindung eine Schubkraft T (siehe Bild 23), deren Wert, wenn kein genauerer Nachweis geführt wird,
beim zweiteiligen Stab (m = 2) mit
| T = Qi * s1 / 2a1 | (67) |
beim dreiteiligen Stab (m = 3) mit
| T = 0,5 * Qi * s1 / 2a1 | (68) |
beim vierteiligen Stab (m = 4) mit
| T ' = 0,4 * Qi * s1 / 2a1 | (69) |
| T '' = 0,3 * Qi * s1 / 2a1 | (70) |
angenommen werden darf.
Die Felderanzahl der Rahmenstäbe muss ≥ 3 sein, so dass die Querverbindungen zumindest in den Drittelspunkten der Stablängen anzuordnen sind. Rahmen- und Gitterstäbe müssen außerdem an den Enden Querverbindungen erhalten, wenn sie nicht durch mindestens zwei hintereinanderliegende Dübel oder vier in einer Nagelreihe hintereinanderliegende Nägel angeschlossen sind.
Jede einzelne Querverbindung ist mindestens durch zwei Dübel oder vier Nägel an jeden Einzelstab anzuschließen. Bei verleimten Zwischenhölzern soll die Länge eines Zwischenholzes mindestens doppelt so groß sein wie der lichte Abstand der Einzelstäbe. Die Aufnahme des Biegemomentes aus der Schubkraft T braucht bei Zwischenhölzern nicht nachgewiesen zu werden, solange die Spreizung a/h1 ≤ 2 ist.
Bei Gitterstäben nach Bild 22f und Bild 22g ist der Querverband für die mit der ideellen Querkraft Qi nach Gleichung (63) bestimmten Gesamtstrebenkraft (ND = Qi/sin α) bzw. Gesamtpfostenkraft (NP = Qi) zu bemessen. Jeder Einzelstab des Querverbandes ist mit mindestens vier einschnittigen Nägeln anzuschließen (siehe auch DIN 1052 Teil 2, Abschnitt 6.2.1).
9.4 Ausmittiger Druck (Druck und Biegung)
Stäbe, deren Druckkraft ausmittig an einem planmäßigen Hebelarm angreift oder deren Achse schon im lastfreien Zustand eine planmäßig festgelegte Krümmung hat, oder Stäbe, die außer durch eine Druckkraft noch zusätzlich quer zur Stabachse beansprucht werden, gelten als planmäßig ausmittig gedrückte Stäbe.
Für derartige Stäbe ist zuerst die gewöhnliche Spannungsuntersuchung auf Druck und Biegung ohne Berücksichtigung des Einflusses der Ausbiegung durchzuführen:
| N /Αn | + | M / Wn | ≤ 1 | (71) |
| zul oD|| | zul oB |
Hierbei sind für zul oD|| bzw zul oB die maßgebenden Werte in den Tabellen 5 bzw. 6 unter Berücksichtigung der Abschnitte 5.1 und 5.2 einzusetzen. Querschnittsschwächungen sind nach Abschnitt 6.4 zu berücksichtigen.
Sodann ist, falls kein genauerer Nachweis erfolgt, der Stabilitätsnachweis nach der Gleichung
| N / A | + | M / W | ≤ 1 | (72) |
| zul ok | kB * 1,1 * zul oB |
zu führen, wobei zul ok nach Gleichung (59) zu ermitteln ist; dabei ist für ω stets der größte Wert ohne Rücksicht auf die Richtung der Ausbiegung einzusetzen. kB ist nach den Gleichungen (48) bis (50) zu berechnen.
Bei zusammengesetzten Stäben mit nachgiebigen Verbindungsmitteln ist der Betrag der Biegespannung nach Abschnitt 8.3 unter Berücksichtigung des wirksamen Flächenmomentes 2. Grades ef I zu berechnen. Rahmen- und Gitterstäbe nach Bild 22 sollen in der Regel nur zentrisch belastet werden. Rechtwinklig zur stofffreien Achse dürfen derartige Stäbe nur aus Wind- oder sonstigen Zusatzlasten, deren Wirkung nachzuweisen ist, beansprucht werden.
9.5 Stöße
Bei Stößen von planmäßig mittig beanspruchten Druckstäben, die als Kontaktstöße (Passstöße) gegebenenfalls unter Anwendung geeigneter Hilfsmittel hergestellt sind, genügt es, die verbundenen Teile durch Laschen in ihrer gegenseitigen Lage zu sichern. Dies ist aber nur zulässig in den äußeren Viertelteilen der Knicklänge. Dabei sind die Verbindungsmittel für die halbe Druckkraft (ohne Knickzahl) nachzuweisen.
In allen anderen Fällen sind die Flächenmomente 2. Grades des Druckstabes in beiden Richtungen voll durch die Stoßdeckung zu ersetzen und die ganze Druckkraft durch die Verbindungsmittel aufzunehmen. Erforderlichenfalls ist die Nachgiebigkeit der Verbindungsmittel an der Stoßstelle zu berücksichtigen.
Bild 23. Annahmen über die Angriffspunkte der Quer- und Schubkräfte bei mehrteiligen Rahmenstäben (Beispiel: Rahmenstäbe mit Bindehölzern)
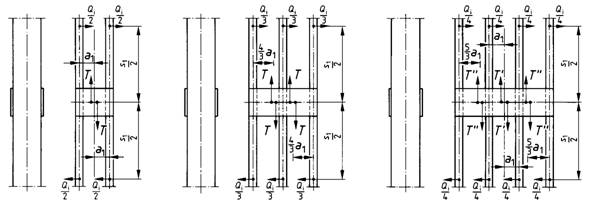

9.6 Tragsicherheitsnachweis nach der Spannungstheorie II. Ordnung
9.6.1 Anstelle der Knicksicherheitsnachweise nach den Abschnitten 9.1 bis 9.4 darf für Tragsysteme, die in ihrer Ebene nicht durch Verbände, Scheiben oder dergleichen ausgesteift sind, z.B. Rahmensysteme nach Bild 25, auch der Tragsicherheitsnachweis nach der Spannungstheorie II. Ordnung geführt werden. Es ist ausreichend, wenn einer der beiden Nachweise geführt wird.
Die Nachgiebigkeit der Verbindungsmittel sowie die Kriechverformungen sind gegebenenfalls zu berücksichtigen.
Es darf ein linearer Zusammenhang zwischen der Steifigkeit des Tragwerkes und seiner Verformung zugrunde gelegt werden. Die Biege-, Dehn- und Schubsteifigkeiten sind mit den Elastizitäts- und Schubmoduln nach den Tabellen 1 bis 3 zu ermitteln, die Federsteifigkeiten nachgiebiger Anschlüsse mit den 0,8 fachen Werten der Verschiebungsmoduln nach DIN 1052 Teil 2, Abschnitt 13.
Die Kriechzahl darf nach Abschnitt 4.3 bestimmt werden. Erforderlichenfalls ist ein angemessener Anteil der Verkehrslast als ständig wirkend anzunehmen.
9.6.2 Die Schnittgrößen nach der Theorie II. Ordnung sind für die γ1- bzw. γ2-fachen Lasten zu ermitteln. Dabei sind Vorverformungen nach den Abschnitten 9.6.3 bis 9.6.6 zu berücksichtigen. Die Kriechverformungen dürfen als zusätzliche Vorverformungen in Rechnung gestellt werden.
Der Nachweis ausreichender Tragsicherheit ist erbracht, wenn folgende Bedingungen eingehalten werden:
Als Lasterhöhungsbeiwerte sind für beide Lastfälle H und HZ γ1 = 2,0 und γ2 = 3,0 einzusetzen.
9.6.3 Bei planmäßig geraden, mittig gedrückten Stäben ist im Hinblick auf baupraktisch unvermeidbare Imperfektionen rechnerisch eine wahlweise sinus- oder parabelförmige Vorkrümmung der Stabachse zu berücksichtigen.
Hierbei ist in Stabmitte eine rechnerische Ausmitte
| e = η * k * s / i | (73) |
anzusetzen (siehe Bild 24).
Hierin bedeuten:
| e | ungewollte Ausmitte der Stabachse bei unbelastetem Stab | |
| s | Netzlänge des Stabes | |
| i k | Trägheitsradius bzw. Kernweite des Querschnittes, bei zusammengesetzten Stäben ohne Berücksichtigung etwaiger Nachgiebigkeiten der Verbindungsmittel | |
| η | Vorkrümmungsbeiwert | |
| η= 0,003 | für Stäbe aus Brettschichtholz | |
| η = 0,006 | für Vollholz - Stäbe aus Nadelholz der Güteklassen I und II sowie aus Laubholz mittlerer Güte. | |
Für k ist bei unsymmetrischen Querschnitten der größere Wert einzusetzen.
9.6.4 Bei Rahmentragwerken ist zusätzlich eine ungewollte Schrägstellung der Stiele des unbelasteten Tragwerkes in ungünstigster Richtung zu berücksichtigen. Entsprechendes gilt auch für einzelne Stützen und Stützenreihen (siehe Bild 25).
Hierbei ist als rechnerische Abweichung von der Sollage des Stieles anzusetzen
| ψ = ± 1 / 100 * h0,5 | (74) |
Darin ist h die Stiel- oder Stützenhöhe in m, bei mehrgeschossigen Rahmen die gesamte Tragwerkshöhe.
Bild 24. Stab mit ungewollter Ausmitte e im unbelasteten Zustand
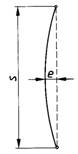
Bild 25: Rahmensysteme, Einzelstützen und Stützenreihen mit ungewollter Schrägstellung der Stiele
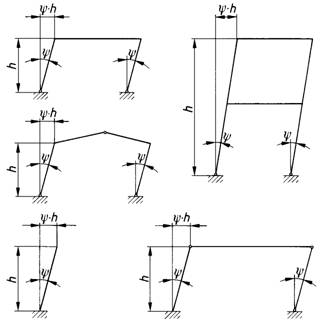
9.6.5 Bei planmäßig ausmittig gedrückten Stäben ist die rechnerische Ausmitte e nach Gleichung (73) zusätzlich zu berücksichtigen. Dies ist nicht erforderlich, wenn die planmäßige Ausmitte M / N, bezogen auf den maßgebenden Querschnitt - am Stabende oder in Stabmitte -, mindestens 20 * e beträgt.
9.6.6 Bei Rahmentragwerken, deren Stiele eine planmäßige Ausmitte M / N in m aufweisen, die ≥ 1/5 * h0,5 (h in m) ist, braucht die Schrägstellung der Stiele nach Abschnitt 9.6.4 nicht angesetzt zu werden.
Entsprechendes gilt sinngemäß auch für einzelne Stützen und Stützenreihen.
9.6.7 Die Durchbiegungsnachweise nach Abschnitt 8.5 dürfen für den Gebrauchszustand nach Theorie I. Ordnung geführt werden.
10 Verbände, Scheiben, Abstützungen
10.1 Aussteifung von Druckgurten biegebeanspruchter Bauteile
Biegeträger sowie Druckgurte von Fachwerkträgern müssen gegen seitliches Ausweichen gesichert sein.
Bei Biegeträgern ist der Nachweis gegen seitliches Ausweichen nach Abschnitt 8.6 zu führen. Bei Fachwerkträgern ist der Nachweis für den gedrückten Gurt nach Abschnitt 9.3 unter Berücksichtigung des Abschnittes 9.1.2 oder gegebenenfalls nach Abschnitt 9.4 zu führen.
10.2 Bemessungsgrundlagen
10.2.1 Allgemeines
Wenn keine Einzelabstützungen gegen feste Punkte oder durch Stäbe, Halbrahmen oder dergleichen vorgenommen werden, müssen Aussteifungsträger, -scheiben oder -verbände angeordnet werden.
10.2.2 Druckgurte von Fachwerkträgern
Zur Bemessung der Aussteifungskonstruktion für Druckgurte von Fachwerkträgern ist, wenn ein genauerer Nachweis nicht geführt wird, eine gleichmäßig verteilte Seitenlast von
| qs = m * NGurt / 30 * l | (75) |
rechtwinklig zur Trägerebene nach beiden Richtungen wirkend anzunehmen.
Hierin bedeuten:
| m | Anzahl der auszusteifenden Druckgurte |
| NGurt | mittlere Gurtkraft für den ungünstigsten Lastfall |
| l | Stützweite der Aussteifungskonstruktion. |
10.2.3 Biegeträger mit Rechteckquerschnitt
Zur Bemessung. der Aussteifungskonstruktion für Biege-träger mit Rechteckquerschnitt, bei denen das Verhältnis Höhe zu Breite d 10 ist, darf eine gleichmäßig verteilte Seitenlast von
| qs | = | m * max M | (76) |
| 350 * l * b |
rechtwinklig zur Trägerebene nach beiden Richtungen wirkend angenommen werden, wenn ein genauerer Nachweis nicht geführt wird. Dieser ist bei einem Seitenverhältnis > 10 stets zu führen.
Hierin bedeuten:
| m | Anzahl der auszusteifenden Träger |
| max M | maximales Biegemoment des Einzelträgers aus lotrechter Last |
| b | Trägerbreite |
| l | Stützweite der Aussteifungskonstruktion. |
Die Aussteifungskonstruktion muss an die Druckgurte der Träger angeschlossen sein.
10.2.4 Gleichzeitige Wirkung von Wind- und Seitenlast
Für Bauteile in Konstruktionen, die zur Aussteifung von gedrückten Fachwerkgurten oder von Biegeträgern dienen und die Windlasten aufzunehmen haben, sind die Wirkungen aus der Seitenlast mit denen aus der vollen Windlast nach DIN 1055 Teil 4 zu überlagern, wenn die Stützweite ≥ 40 m ist; bei einer Stützweite ≤ 30 m genügt die Überlagerung mit den Wirkungen aus der halben Windlast. Dabei gelten die zulässigen Spannungen im Lastfall HZ. Für Stützweiten zwischen 30 m und 40 m darf geradlinig interpoliert werden.
Unter der Wind- oder Seitenlast allein sind in diesen Bauteilen die zulässigen Spannungen im Lastfall H einzuhalten.
10.2.5 Durchbiegungsbeschränkungen und konstruktive Maßnahmen
Die rechnerische horizontale Ausbiegung der Aussteifungskonstruktion darf bei Anwendung der Gleichung (75) bzw. Gleichung (76) 1/1000 der Stützweite nicht überschreiten. Der Durchbiegungsnachweis ist in der Regel entbehrlich, wenn das Verhältnis Höhe zu Spannweite der Aussteifungskonstruktion ≥ 1/6 ist.
Mit Rücksicht auf die Verformungen der Konstruktionsteile zwischen den Aussteifungskonstruktionen und auf die Nachgiebigkeit der dort vorhandenen Verbindungsmittel sind bei Gebäudelängen über 25 m mindestens zwei Aussteifungskonstruktionen anzuordnen; jedoch soll deren lichter Abstand in der Regel 25 m nicht überschreiten, wenn kein genauerer Nachweis erfolgt.
10.3 Scheiben
10.3.1 Allgemeines
Scheiben nach den nachstehenden Festlegungen dürfen zur Aufnahme und Weiterleitung von vorwiegend ruhenden Lasten (einschließlich Windlasten) sowie Erdbebenkräften in Scheibenebene in Rechnung gestellt werden. Sie bestehen entweder aus Platten aus Holzwerkstoffen, die durch die mit ihnen kraftschlüssig verbundene Unterkonstruktion (z.B. Träger oder Binder mit Pfetten) zu einer Scheibe zusammengeschlossen werden, oder aus Tafeln, sofern die Stützweite nicht mehr als 30 m beträgt (siehe Abschnitt 11.3). Die Oberkanten der Unterkonstruktion sollen vorzugsweise in derselben Ebene liegen.
Sind parallel zur Spannrichtung einer Scheibe aus Holzwerkstoffen mehr als zwei nicht unterstützte Stöße vorhanden (siehe Bild 26), so ist die Scheibenstützweite ls auf 12,50 m zu beschränken.
Die rechnerische Durchbiegung der Platten aus Holzwerkstoffen infolge vertikaler Flächenlast von (g + s) bzw. (g + p) darf 1/400 ihrer Stützweite nicht überschreiten.
10.3.2 Scheiben mit rechnerischem Nachweis
Beim Spannungsnachweis für Platten aus Holzwerkstoffen und für die Unterkonstruktion sind die Spannungen aus allen Beanspruchungen (d. h. einschließlich Scheibenbeanspruchung) zu berücksichtigen. Die zulässige Durchbiegung der Scheibe beträgt 1/1000 der Scheibenstützweite ls.
10.3.3 Scheiben ohne rechnerischen Nachweis
Für die Mindestdicken der Platten aus Holzwerkstoffen gilt in Abhängigkeit von der Scheibenstützweite Tabelle 12. Ihre kleinste Seitenlänge muss mindestens 1,0 m betragen.
Für Scheibensysteme mit Seitenverhältnissen hs/ls ≥ 0,25 darf ein Durchbiegungsnachweis entfallen.
Bei Einhaltung der in Tabelle 12 und Bild 26 angegebenen Ausführungsbedingungen und unter Beachtung der konstruktiven Anforderungen nach Abschnitt 10.3.1 ist ein rechnerischer Nachweis der Scheibenwirkung und der Durchbiegung in Scheibenebene nicht erforderlich. Beim Nachweis rechtwinklig zur Scheibenebene dürfen die Spannungen aus der Scheibenwirkung in den Holzwerkstoffen und der zugehörigen Unterkonstruktion vernachlässigt werden.
Der Nagelabstand nach Tabelle 12 in der zur Aussteifung in Rechnung gestellten Scheibenfläche ist konstant einzuhalten.
Für den Nagelabstand rechtwinklig zum Plattenrand (Plattenstoß auf Unterkonstruktion) gilt Bild 26.
Die Sparrenpfetten am Scheibenrand (siehe Bild 26) sind mindestens 1,5fach so breit wie die inneren Sparrenpfetten auszuführen.
Tabelle 12: Ausführungsbestimmungen für Scheiben ohne Nachweis
| Gleichmäßig verteilte Horizontallast qh
kN/m | Scheibenstützweite ls
| Mindestdicken der Platten | Erforderlicher Nagelabstand e für Nageldurchmesser 3,4 mm1) bei einer Scheibenhöhe hs | ||||
| Flachpressplatten mm | Bau-Furniersperrholz mm | ≥ 0,25 ls mm | ≥ 0,50 ls mm | ≥ 0,75 ls mm | 1,0 ls mm | ||
| ≤ 2,5 | ≤ 25 | 19 | 12 | 60 | 120 | 180 | 200 |
| ≤ 3,5 | ≤ 30 | 22 | 12 | 40 | 90 | 130 | 180 |
| 1) Bei Verwendung anderer Nageldurchmesser bis 4,2 mm ist der erforderliche Nagelabstand e im Verhältnis der zulässigen Nagelbelastungen umzurechnen; der Nagelabstand darf 200 mm nicht überschreiten. | |||||||
Bild 26. Aussteifende Scheibe mit unterstützten Plattenstößen in Lastrichtung und nicht unterstützten Plattenstößen parallel zur Spannrichtung
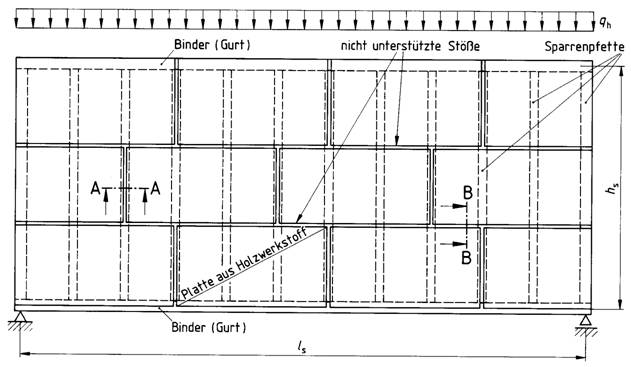
Unterstützter Plattenstoß
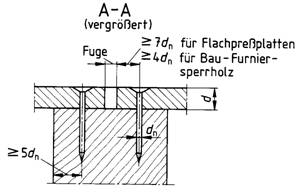
Nicht unterstützter Plattenstoß
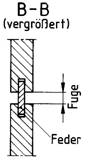
10.4 Abstützung durch Dachlatten und Schalung
Dachlatten dürfen für die seitliche Stützung gedrückter Gurte nicht als ausreichend angesehen werden mit Ausnahme der seitlichen Stützung von knickgefährdeten Sparren und von Fachwerk-Obergurten mit mindestens 40 mm Breite bei Dächern bis zu 15 m Spannweite und einem maximalen Sparren- bzw. Binderabstand von 1,25 m, wenn die Querschnittshöhe der Sparren nicht mehr als das Vierfache der Querschnittsbreite beträgt.
Bei Dachbindern mit mindestens 40 mm breiten Gurten, bei denen die ständige Last weniger als 50 % der Gesamtlast ausmacht, dürfen rechtwinklig zu den auszusteifenden Gurten verlaufende Dachschalungen aus Einzelbrettern zur seitlichen Abstützung herangezogen werden, wenn die Vernagelung des Einzelbrettes (Breite b ≥ 120 mm) durch mindestens zwei Nägel mit jedem Gurt, auch an jedem Brettstoß, einwandfrei ausgeführt werden kann (siehe DIN 1052 Teil 2), der Binderabstand 1,25 m und die Binderspannweite 12,50 m nicht überschreiten und die Länge der Dachfläche mindestens das 0,8fache der Binderspannweite, aber höchstens 25 m, beträgt. Dabei sind die Brettstöße um mindestens zwei Binderabstände gegeneinander zu versetzen, und die Stoßbreite darf nicht mehr als 1,0 m betragen. Die Dachschalung ist hierbei kraftschlüssig mit den Windverbänden oder entsprechenden Konstruktionen zu verbinden.
Zur Aufnahme von parallel zur Lattung bzw. Brettrichtung wirkenden Windlasten sind gesonderte Verbände anzuordnen.
10.5 Einzelabstützungen zur Unterteilung der Knicklänge
Teile, welche ein Druckglied zur Unterteilung der Knicklänge in Zwischenpunkten nach Abschnitt 9.1.1 abstützen, sind in der Regel für eine Stützeinzellast bei Vollholz von
| K = N / 50 | (77) |
und bei Brettschichtholz von
| K = N / 100 | (78) |
zu bemessen. Hierin bedeutet N die größte Stabkraft (ohne Knickzahl) der an die Abstützung angrenzenden Druckstäbe. Wird ein Teil zur Abstützung mehrerer Druckglieder herangezogen (siehe Bild 27), so müssen die entsprechenden Stützkräfte in den einzelnen Bereichen aufgenommen werden.
Bild 27. Einzelabstützung von Druckgliedern

Teile, welche ein Druckglied zur Unterteilung der Knicklänge nach Abschnitt 9.1.1 gegen einen Aussteifungsverband nach Abschnitt 10.2 abstützen, sind für die auf sie entfallende anteilige Seitenlast qs, mindestens aber für eine Stützeinzellast nach Gleichung (77) bzw. Gleichung (78) zu bemessen und anzuschließen. Der ungünstigere Wert ist maßgebend.
11 Holztafeln
11.1 Allgemeines
11.1.1 Baustoffe, Mindestdicken und Querschnittsschwächungen
Für die Beplankung von Tafeln darf die Holzwerkstoff-klasse 20 nach DIN 68 800 Teil 2 verwendet werden, sofern nicht aus Gründen des Holzschutzes andere Holzwerkstoffklassen erforderlich werden.
Bei Tafeln sind die in Tabelle 13 angegebenen Mindestdicken, örtliche Schwächungen ausgenommen, einzuhalten. Rippen aus Bauschnittholz müssen mindestens der Güteklasse II, Schnittklasse A nach DIN 4074 Teil 1 entsprechen. Sie müssen auf die Mindestdicke von 24 mm frei von Baumkanten sein. Bei Rippen unter Beplankungsstößen muss auf beiden Seiten des Stoßes die Scharfkantigkeit auf je 24 mm Dicke, bei verleimten Tafeln (ausgenommen Nagelpressleimung) auf je 12 mm Dicke vorliegen.
Tabelle 13. Mindestdicken bei Tafeln
| Baustoff | Mindestdicken für | |
| Rippen1) mm | Beplankungen mm | |
| Bauschnittholz Brettschichtholz | 24 | - |
| Bau-Furniersperrholz | 15 | 6 |
| Flachpressplatten | 16 | 8 |
| 1) Querschnittsfläche für Bauschnittholz mindestens 14 cm2, bei Holzwerkstoffen mindestens 10 cm2. | ||
Aussparungen in mittragenden Beplankungen dürfen beim Nachweis der Spannungen vernachlässigt werden, wenn auf einer Fläche von 2,5 m2 einer Tafel die Gesamtfläche aller Aussparungen höchstens 300 cm2 beträgt. Dabei darf die größte Ausdehnung der einzelnen Öffnung 200 mm nicht überschreiten; dieser Höchstwert gilt auch für die Summe aller Aussparungsbreiten innerhalb des Querschnittes einer Tafel.
11.1.2 Feuchtegehalt
Der Feuchtegehalt des Holzes darf bei der Herstellung der Tafeln 18 %, für zu verleimende Teile 15 % nicht überschreiten.
11.1.3 Tragende Verbindungen
Verbindungen mit Hirnholz sowie mit Schnittflächen von Platten dürfen nicht als tragend in Rechnung gestellt werden, ausgenommen die Verleimung von Holzwerkstoff-Beplankungen mit den Schnittflächen von Holzwerkstoff-Rippen.
Bei Leimverbindungen muss die Breite der Leimfläche zwischen Rippe und Beplankung mindestens 10 mm betragen. Nagelpressleimung zwischen Vollholzrippen und Beplankung darf angewendet werden, wenn Abschnitt 12.5 eingehalten wird.
11.2 Auf Druck oder Biegung beanspruchte Tafeln (siehe Bilder 1a, 1c, 1d)
11.2.1 Allgemeines
Mittragende Beplankungen aus Holzwerkstoffen dürfen auch einseitig aufgebracht werden. Aussteifende Beplankungen dürfen einseitig aufgebracht werden, wenn das Seitenverhältnis Höhe zu Breite der auszusteifenden Rippe nicht größer als 4 ist.
Bei Verbundquerschnitten sind die Knickzahlen für den Rippenwerkstoff zugrunde zu legen.
Die Biegerandspannungen in den Rippen dürfen die zulässigen Werte für Biegung, die Schwerpunktsspannungen in den Beplankungen die zulässigen Werte für Druck bzw. Zug nicht überschreiten.
Die Erhöhung der zulässigen Biegespannung nach Abschnitt 5.1.8 gilt nur für Rippen aus Holz.
Der Durchsenkungsanteil aus der Schubverformung darf bei Tafeln mit Rippen aus Holz vernachlässigt werden.
Stumpfe Stöße der Beplankung sind beim Spannungsnachweis zu berücksichtigen. Die Beplankung darf in diesen Fällen bei verleimten Tafeln erst im Abstand b (lichter Abstand der Rippen) von der Stoßstelle, bei nachgiebig angeschlossenen Beplankungen erst ab der Stelle, an der die von der Beplankung aufzunehmende Längskraft eingeleitet ist, in Rechnung gestellt werden. Für den Durchbiegungs- und Knicknachweis dürfen Beplankungsstöße in der Regel vernachlässigt werden.
Bild 28. Mitwirkende Beplankungsbreiten
beidseitige Beplankung

einseitige Beplankung

11.2.2 Mitwirkende Beplankungsbreite
Beplankungen aus Holzwerkstoffen dürfen mit den Breiten
| bM = b' + b2 | (79) |
bzw.
| bR = b' / 2 + b2 + ü' | (80) |
nach Bild 28 als mitwirkend in Rechnung gestellt werden.
Hierin bedeuten:
| bM bR | mitwirkende Beplankungsbreite je Rippe im Mittel- bzw. Randbereich |
| b | lichter Abstand der Rippen |
| b' | mitwirkende Breite zwischen den Rippen |
| b2 | Rippenbreite |
| ü | seitlicher Überstand der Beplankung |
| ü' | mitwirkende Breite des seitlichen Überstandes |
| h | Gesamtquerschnittshöhe |
| l | Feldlänge bzw. Teilfeldlänge. |
Als Feldlänge l ist bei Deckentafeln der Abstand der Biegemomentennullpunkte ohne Berücksichtigung der feldweisen Veränderung von Lasten (bei Tafeln auf zwei Stützen ohne Auskragung die Stützweite) und bei knickbeanspruchten
Tafeln die maßgebende Knicklänge einzusetzen. Bei nicht vernachlässigbaren Aussparungen oder anderen Unterbrechungen der Beplankung quer zur Spannrichtung der Tafel (z.B. Beplankungsstöße) dürfen höchstens die durch die Unterbrechung begrenzten Teilfeldlängen eingesetzt werden.
Die Breiten b' und ü' sind je Feldlänge l und je lichter Weite b zu ermitteln, wobei zwischen Gleichstreckenlast in Spannrichtung der Tafel und Einzellast (auch Linienlast quer zur Spannrichtung) zu unterscheiden ist.
Bei quer zur Tafelspannrichtung gleichmäßig verteilter Last oder wenn eine gleichmäßige Verteilung angenommen werden kann, z.B. bei Vorhandensein von Querrippen mit annähernd gleichen Querschnittsabmessungen wie die Längsrippen, dürfen die mitwirkenden Rand- und Mittelbereiche einer Tafel zu einem Querschnitt zusammengefasst werden. Im anderen Falle sind alle Nachweise für jeden Bereich getrennt zu führen.
Bei Gleichstreckenlast darf, sofern kein genauerer Nachweis geführt wird, bei b/l ≤ 0,4
für Bau-Furniersperrholz
| b' / b = 1,06 - 1,4 * b / l | (81) |
und für Flachpressplatten
| b' / b = 1,06 - 0,6 * b / l | (82) |
angenommen werden; dabei ist stets b' ≤ b einzuhalten. Die mitwirkende Breite b'F für Einzellast ergibt sich bei b / l ≤ 0,4 annähernd
für Bau-Furniersperrholz zu
| b'F /b = 1 - 1,8 * b / l | für l / cF ≤ 5 | (83) |
| b'F / b = 1 - 2,6 * b / 1,
jedoch ≥ 0,2 | für 5 < l / cF ≤ 20 | (84) |
und für Flachpressplatten zu
| b'F / b = 1 - 0,9 * b / l | für l / cF ≤ 5 | (85) |
| b'F / b = 1 - 1,4 * b / l | für 5 < l / cF ≤ 20 | (86) |
Überstände ü, die nicht durch Nachbarelemente gehalten sind, dürfen höchstens mit ü' = b2 angesetzt werden; im übrigen ist ü' / ü wie b' / b zu berechnen, wobei b / l gleich 2 * ü / l zu setzen ist.
cF ist die Summe aus der Lastaufstandslänge in Spannrichtung der Tafel und der zweifachen Gesamtquerschnittshöhe h der Tafel.
Liegt die Lastwirkungslinie näher als das Maß b an einem Biegemomentennullpunkt oder ist l / cF > 20, so ist b'F = 0 zu setzen.
Im Bereich der Stützmomente durchlaufender oder auskragender Tafeln ist für den Spannungsnachweis immer von Einzellasten auszugehen.
Beim Durchbiegungsnachweis und bei der Ermittlung der Schnittkräfte darf stets die mitwirkende Breite für Gleichstreckenlast eingesetzt werden.
11.2.3 Querschnittswerte
Die Querschnittswerte für den Mittel- oder Randbereich von Tafeln mit ein- oder beidseitiger Beplankung sind unter Berücksichtigung der Verhältnisse ni = Ei / Ev zu ermitteln (Beispiel für einen dreiteiligen Querschnitt siehe Bild 29).
Hierin bedeuten:
| E1 E3 | Druck- bzw. Zug-Elastizitätsmodul der Beplankung |
| E2 | Elastizitätsmodul von Voll- oder Brettschichtholzrippen bzw. Biege-Elastizitätsmodul von überwiegend auf Biegung beanspruchten Rippen aus Holzwerkstoffen bzw. Druck-Elastizitätsmodul von überwiegend auf Druck beanspruchten Rippen aus Holzwerkstoffen |
| Ev | beliebiger Vergleichs-Elastizitätsmodul. |
Die Beplankungen dürfen mit den Breiten bM bzw. bR nach Abschnitt 11.2.2 als mitwirkend in Rechnung gestellt werden.
Werden Beplankungen und Rippen miteinander verleimt, so darf die Verbindung als starr angesehen werden.
Bei Verwendung mechanischer Verbindungsmittel nach DIN 1052 Teil 2 ist deren Nachgiebigkeit zu berücksichtigen. Die Querschnittswerte dürfen, auch für unsymmetrische Querschnitte (siehe Bild 29), nach Abschnitt 8.3 berechnet werden.
Bild 29. Unsymmetrischer Querschnitt mit beidseitiger Beplankung
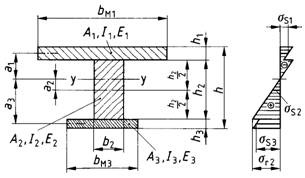
11.2.4 Rippenabstände
Beplankungen aus Holzwerkstoffen sind durch Längsrippen in lichten Abständen von
| b ≤ 1,25 * h1,3 * (EBv / oDx)0,5 | (87) |
auszusteifen, höchstens jedoch im Abstand b = 50 * h1,3.
Hierin bedeuten:
| h1 h3 | Dicke der Beplankung |
| EBv = (EBx * EBy)0,5 | Vergleichsbiege-Elastizitätsmodul der Beplankung |
| oDx | Druckspannung in der Beplankung (ohne Knickzahl). |
Bei unterschiedlicher Beplankungsdicke ist der kleinere Wert für b maßgebend.
11.3 Decken- und Dachscheiben aus Tafeln
11.3.1 Allgemeines
Decken- und Dachscheiben nach den nachstehenden Festlegungen dürfen mit Stützweiten bis 30 m für die Aufnahme und Weiterleitung von vorwiegend ruhenden Lasten (einschließlich Windlasten und Erdbebenkräften) in Scheibenebene in Rechnung gestellt werden. Sie dürfen vereinfachend als Balken berechnet werden.
Die Scheibenhöhe hs muss mindestens 1/4 der Stützweite ls betragen (siehe Bild 30). Bei Scheiben, deren Höhe hs größer als die Stützweite ls ist, darf für hs höchstens der Wert für ls zugrunde gelegt werden.
11.3.2 Durchbiegungen
Die zulässige Durchbiegung beträgt 1/1000 der Stützweite ls. Die Schubverformung ist zu berücksichtigen. Der Nachweis der Durchbiegung darf für Scheiben entfallen, deren Stützweite ls höchstens gleich der zweifachen Scheibenhöhe hs ist.
Stoßfugen in den Beplankungen der einzelnen Tafeln brauchen nicht berücksichtigt zu werden, wenn sie parallel zur Lastrichtung liegen und ihr Abstand untereinander sowie vom Scheibenauflager mindestens ls / 4 beträgt.
Bei Stoßabständen zwischen ls / 4 und ls / 8 ist die rechnerische Steifigkeit des Gesamtquerschnittes um 1/3 abzumindern. Stoßabstände kleiner als ls/8 sind unzulässig.
11.4 Wandscheiben aus Tafeln
11.4.1 Allgemeines
Wandscheiben aus Tafeln werden durch waagerechte Lasten in Tafelebene nach Bild 1b, zusätzlich gegebenenfalls durch lotrechte Lasten nach Bild 1a oder waagerechte Lasten nach Bild 1c beansprucht.
Tafeln, die nur nach Bild 1a oder nach Bild 1c belastet werden, sind nach Abschnitt 11.2 zu bemessen.
Die Angaben nach Abschnitt 11.4 gelten für Wandscheiben ohne Öffnungen. Sofern kein genauerer Nachweis erfolgt, sind sie nach den Abschnitten 11.4.2 und 11.4.3 zu bemessen. Sollen Wandscheiben mit Öffnungen, z.B. Fenster, für die Ableitung der Lasten rechnerisch in Ansatz gebracht werden, so muss ihr Tragverhalten unter Berücksichtigung der Öffnungen ermittelt werden.
Man unterscheidet zwischen Einraster-Tafeln (siehe Bild 31a) und Mehrraster-Tafeln (siehe Bild 31b). Die Breite b eines Rasters wird begrenzt durch den Abstand der Randrippen, gegebenenfalls auch durch den Abstand der lotrechten Beplankungsstöße oder durch höchstens etwa 0,5 x Tafelhöhe.
Bild 30. Beispiele für Dach- oder Deckenscheiben aus Tafeln (Draufsicht); Maße, Last
a) hs < ls

b) hs > ls
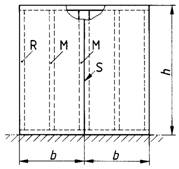
Bild 31. Beispiele für Einraster- und Mehrraster-Tafeln
| R | Randrippe |
| M | Mittelrippe |
a) Einraster-Tafel

b) Zweiraster-Tafel mit Beplankungsstoß S

11.4.2 Bemessung von Wandscheiben für die waagerechte Last FH in Tafelebene
11.4.2.1 Wandscheiben aus Einraster-Tafeln
Die nachstehenden Festlegungen gelten für Tafelbreiten b von mindestens 0,60 m.
Die Aufnahme und Weiterleitung folgender Kräfte sind nachzuweisen:
| D1 = α1 * FH * h / bs1 | (88) |
| ZA = FH * h / bs1 | (89) |
Bild 32. Anker-Zugkraft ZA und Druckkraft D1 im Schwellenbereich

Bild 33. Verteilung und Anschluss der Streben-Zugkraft Z bei einseitiger Beplankung
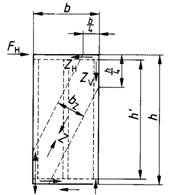
Die Beplankungen sowie ihr Anschluss brauchen bei beidseitig beplankten Tafeln mit einer Breite b von mindestens 1,0 m nicht nachgewiesen zu werden. Der Höchstabstand der Verbindungsmittel ist einzuhalten.
Die zulässige Auslenkung der Tafeln im Kopfbereich beträgt 1/500 der Tafelhöhe h. Der Nachweis darf - auch bei Tafeln mit einseitiger Beplankung - entfallen, wenn das Verhältnis Höhe zu Breite der Tafeln ≤ 3,0 ist.
11.4.2.2 Wandscheiben aus Mehrraster-Tafeln
Bild 34. Mehrraster-Tafeln
a) Anker-Zugkraft ZA und Rippen-Druckkräfte Di im Schwellenbereich
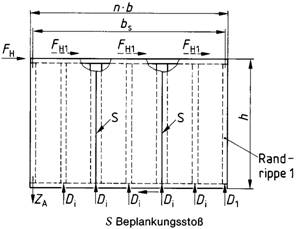
b) Aus Einraster-Tafeln zusammengefügte Tafeln; ZA, Di und Schnittkraft T

Mehrraster-Tafeln mit n Rastern (siehe Bild 34) werden sinngemäß nach Abschnitt 11.4.2.1 bemessen.
Die Druckkräfte D; der Rippen im Schwellenbereich ergeben sich aus
| Di = αi * FH * h / bs | (90) |
wobei αi Tabelle 14 zu entnehmen ist.
Die Anker-Zugkraft ZA = FH * h / bs braucht nur am zugbeanspruchten Rand der Gesamttafel aufgenommen zu werden.
Tabelle 14. Faktoren α1 und αi für Tafeln mit einer Rasterbreite b ≥ 1,20 m
| Beplankung | Anzahl n der Raster | Randrippe 1 α1 | übrige Rippen αi |
| beidseitig | 1 | 2/31) | 0 |
| 2 | 2/3 | 1/5 | |
| > 2 | 1/2 | 1/5 | |
| einseitig | 1 | 3/41) | 0 |
| ≥ 2 | 3/4 | 2/5 | |
| 1) Für Tafelbreite b = 0,60 m ist α1 = 1,0; Zwischenwerte für Tafelbreiten von 0,60 m bis 1,20 m dürfen geradlinig interpoliert werden. | |||
Werden Mehrraster-Tafeln durch Zusammenfügen von Einraster-Tafeln gebildet, so ist deren Verbindung schubsteif auszubilden.
Sofern kein genauerer Nachweis erfolgt, sind die Verbindungsmittel für die Schubkraft T = ZA zu bemessen (siehe Bild 34b). Ferner sind im Kopf- und erforderlichenfalls auch im Fußbereich durchgehende Gurte anzuordnen, deren Anschlüsse für die Weiterleitung der waagerechten Last FH zu bemessen sind.
11.4.3 Nachweis der Schwellenpressung bei Wandtafeln infolge lotrechter Lasten FV
11.4.3.1 Einraster-Tafeln
An der Abtragung der lotrechten Lasten FVi in die Unterkonstruktion beteiligen sich die lotrechten Rippen über Schwellenpressung sowie die Beplankungen über ihren unmittelbaren Anschluss an die Schwelle (siehe Bild 35). Zur Ermittlung der einzelnen Rippen-Druckkräfte Di im Schwellenbereich darf die Gesamtlast ∑ FVi im Verhältnis der jeweiligen zulässigen Rippen-Druckkraft Di zur zulässigen Gesamtlast zul D = ∑ (zul Di) + zul DBepl aufgeteilt werden.
Die zulässige Anschlusskraft der Beplankung zul DBepl ergibt sich aus der zulässigen Belastung aller in der Schwelle angeordneten Verbindungsmittel. Bei verleimten Tafeln darf dabei die zulässige Druckspannung in der Beplankung nicht überschritten werden.
Bild 35. Einraster-Tafel unter lotrechten Lasten Fm, Rippen-Druckkräfte Di im Schwellenbereich und Anschlusskraft DBepl der Beplankung an die Schwelle

11.4.3.2 Mehrraster-Tafeln
Mehrraster-Tafeln mit n Rastern werden rechnerisch in Einraster-Tafeln zerlegt. Die Ermittlung der Rippen-Druckkräfte Di im Schwellenbereich erfolgt wie in Abschnitt 11.4.3.1 für jede Rasterbreite getrennt. Bei gemeinsamer Rippe zwischen zwei benachbarten Rastern werden Lasten FVi und Rippenquerschnitt rechnerisch je zur Hälfte auf beide Raster verteilt.
11.4.4 Nachweis der Schwellenpressung bei Wandscheiben infolge gleichzeitig wirkender Lasten FH und FV
Die Rippen-Druckkräfte infolge FH nach Abschnitt 11.4.2 und infolge FV nach Abschnitt 11.4.3 sind für den Nachweis der Einhaltung der zulässigen Spannungen im Schwellenbereich zu addieren.
11.4.5 Verteilung der waagerechten Lasten aus der Decken- oder Dachkonstruktion
Die waagerechten Lasten aus der Decken- oder Dachkonstruktion dürfen anteilmäßig - bei einheitlichem Tafelquerschnitt gleichmäßig - auf die einzelnen Raster verteilt werden (siehe Abschnitt 11.4.2.2). Die Decken- bzw. Dachkonstruktion ist entsprechend anzuschließen.
11.5 Ausführung von Tafeln
Stöße von Beplankungen in Richtung der Tragrippen sind immer auf Rippen aus Vollholz oder Brettschichtholz anzuordnen. Beplankungsstöße auf den Schnittflächen von Rippen aus Holzwerkstoffen sind unzulässig. Die Mindestbreite der Leimfläche zwischen Rippe und Beplankung von 10 mm ist bei Beplankungsstößen beiderseits des Stoßes einzuhalten.
An den freien Plattenrändern im Bereich von Beplankungsstößen sind unterschiedliche Durchbiegungen der Beplankungen bei Lasten rechtwinklig zur Plattenebene zu verhindern, z.B. durch Nut-Feder-Verbindung der Platten.
Im Kopf- und Fußbereich von Wandtafeln für Scheiben sind waagerechte Rippen anzuordnen.
Während der Herstellung des Bauwerkes ist dafür zu sorgen, dass die übrige Konstruktion auch vor Fertigstellung der Decken- oder Dachscheibe standsicher ist.
12 Leimverbindungen
12.1 Herstellungsnachweis
Verleimte tragende Holzbauteile dürfen nur verwendet werden, wenn sie von Betrieben hergestellt worden sind, die eine bestimmungsgemäße Herstellung nachgewiesen haben (siehe Anhang A).
Anmerkung: Ein Verzeichnis der Betriebe, die einen solchen Nachweis geführt haben, wird beim Institut für Bautechnik, Reichpietschufer 74-76, 1000 Berlin 30, geführt und in den Mitteilungen des Instituts für Bautechnik veröffentlicht.
Bei allgemein bauaufsichtlich zugelassenen Holzbauteilen sind außerdem die entsprechenden Bestimmungen der Zulassung zu beachten, gegebenenfalls auch ein zusätzlicher Überwachungsnachweis.
12.2 Holzfeuchte zum Zeitpunkt der Verleimung
Für Leimverbindungen dürfen nur Hölzer mit höchstens 15 % Feuchte verwendet werden.
12.3 Längsstöße
Längsstöße sind durch Schäftung mit einer Leimflächenneigung von höchstens 1/10 oder durch eine Keilzinkenverbindung der Beanspruchungsgruppe I nach DIN 68 140 auszuführen.
Der Spannungsnachweis für den keilgezinkten Querschnitt des Bauteiles ist mit dem reduzierten Querschnitt
| red Α = (1 - v) * Α | (91) |
mit v als Verschwächungsgrad nach DIN 68 140 zu führen. Abweichend davon darf bei Vollholz nach Tabelle 1, Zeile 1, und Brettschichtholz nach Tabelle 1, Zeile 2, mindestens der Güteklasse II mit Querschnittsmaßen bis 300 mm der Spannungsnachweis ohne Berücksichtigung des Verschwächungsgrades v geführt werden, wenn
Bei Bauteilen aus Brettschichtholz darf die Schwächung durch die Keilzinkungen der Einzelbretter unberücksichtigt bleiben.
12.4 Leime
Leime für tragende Bauteile müssen die Prüfungen nach DIN 68 141 bestanden haben.
Für Bauteile, die im Gebrauchszustand unmittelbar der Witterung oder in Gebäuden Klimabedingungen ausgesetzt sind, bei denen eine Gleichgewichtsfeuchte von 20 % oder langfristig oder häufig wiederkehrend eine Temperatur im Bauteil von 50 °C überschritten werden kann, dürfen nur Kunstharzleime verwendet werden, die auf ihre Beständigkeit gegen alle Klimaeinflüsse geprüft sind (z.B. Resorcin- oder Melaminharzleim).
12.5 Verleimen und Pressdruck
Der Pressdruck muss möglichst gleichmäßig verteilt auf alle Leimflächen wirken.
Nagelpressleimung, d. h. Aufbringen des Pressdruckes mit Hilfe von Nägeln, ist für das Aufleimen von Brettlamellen bis zu einer Dicke von 33 mm oder Platten aus Holzwerkstoffen bis zu einer Dicke von 50 mm zulässig. Dazu sind Nägel nach DIN 1052 Teil 2 mit Längen von etwa 2,5 x Lamellen- bzw. Plattendicke zu verwenden, wobei mindestens ein Nagel je 65 cm2 Lamellen- bzw. Plattenfläche angeordnet werden muss und der Nagelabstand höchstens 100 mm betragen darf. Hierbei sind die Löcher im Bau-Furniersperrholz bei Platten-dicken über 20 mm mit etwa 85 % des Nageldurchmessers vorzubohren. Das Vorbohren darf entfallen, wenn geeignete Nageleinschlaggeräte verwendet werden.
Bei mehreren Lagen ist jede Lage für sich zu nageln, wobei die Nägel versetzt angeordnet werden müssen.
12.6 Gestaltung und Aufbau der Bauteile aus Brettschichtholz
Die Dicke der zu Brettschichtholz verwendeten Einzelbretter beträgt mindestens 6 mm und darf 33 mm nicht überschreiten. Sie darf bei geraden Bauteilen auf 40 mm erhöht werden, wenn die Bauteile keinen extremen klimatischen Wechselbeanspruchungen ausgesetzt sind.
Bei gekrümmten Bauteilen muss der Biegeradius r1 mindestens 200 * A sein.
Hierbei ist r1 der Biegeradius des Einzelbrettes und A dessen Dicke.
Biegeradien zwischen 200 * A und 150 * A sind zulässig, wenn die Brettdicke der Zahlenwertgleichung
| A ≤ 13 + 0,4 [r1 / A - 150] in mm | (92) |
genügt. Die durch das Krümmen der einzelnen Schichten vor dem Verleimen verursachten Biegespannungen dürfen vernachlässigt werden.
Bei Brettschichtholzquerschnitten mit mehr als 220 mm Breite müssen die Bretter mit mindestens einer in Brettlängsrichtung durchlaufenden Entlastungsnut versehen werden. Die Nuttiefe (Schnitttiefe von Säge oder Fräser) beträgt 1/4 bis 1/5 der Brettdicke, die Nutbreite höchstens 4 mm. Bei Verwendung von nicht genuteten Brettern muss bei Bauteilen mit mehr als 220 mm Breite jede Brettlage aus mindestens zwei Teilen bestehen. Dabei müssen die Längsfugen übereinanderliegender Lagen mindestens um die Brettdicke, jedoch nicht unter 25 mm gegeneinander versetzt sein, sofern die Bretter innerhalb der Brettlagen nicht an den Schmalseiten miteinander verleimt sind.
Bei Bauteilen, die unmittelbar der Witterung ausgesetzt sind, müssen, ungeachtet eines aufzubringenden Schutzanstriches, mindestens die in der Zug- und Druckzone außenliegenden Brettlagen parallel zur Außenseite der Bauteile verlaufen, oder es müssen nach dem Zuschnitt entsprechende Brettlagen angebracht werden.
12.7 Transport und Montage
Beim Transport, bei der Lagerung und bei der Montage der Bauteile ist durch geeignete Maßnahmen sicherzustellen, dass sich ihre Feuchte durch länger einwirkende Einflüsse aus Bodenfeuchte, Niederschlägen sowie infolge Austrocknung nicht unzuträglich verändert (siehe auch DIN 68 800 Teil 2).
13 Ausführung
13.1 Abbund und Montage
13.1.1 Alle Teile eines Tragwerkes sind so zusammenzufügen und zu montieren, dass kein Teil durch Zwängungen oder sonstige Zustände unzulässig beansprucht wird.
13.1.2 Tragende Bolzen und Klemmbolzen von Dübelverbindungen sind nachzuziehen, wenn mit einem erheblichen Schwinden des Holzes gerechnet werden muss. Sie müssen hierzu genügend Gewindelänge aufweisen und bis zur Beendigung des Schwindens zugänglich bleiben.
13.1.3 Bei mit Passbolzen angeschlossenen außenliegenden Metallteilen ist darauf zu achten, dass zur Aufnahme von Loch-Leibungskräften der volle Schaftquerschnitt auf der erforderlichen Länge vorhanden ist.
13.2 Dachschalungen
13.2.1 Dachschalungen unter Dachdeckungen
Für Schalungen als Träger von Dachdeckungen dürfen Holz mindestens der Güteklasse II nach DIN 4074 Teil 1 und Holzwerkstoffe der Holzwerkstoffklasse 100 bzw. 100 G (siehe DIN 68 800 Teil 2) verwendet werden.
Parallel zu den Auflagern verlaufende Stöße dürfen nur auf den unterstützenden Bauteilen (z.B. Pfetten oder Sparren) angeordnet werden. Die Auflagertiefe muss mindestens 20 mm betragen.
Die rechtwinklig zu den Auflagern verlaufenden freien Ränder von Brettern, Bohlen oder Holzwerkstoffen müssen bei einem Verhältnis lichte Weite lw zur Plattendicke d größer als 30 miteinander durch Nut und Feder oder gleichwertige Maßnahmen verbunden werden.
13.2.2 Dachschalungen unter Dachabdichtungen
Zusätzlich zu den Festlegungen nach Abschnitt 13.2.1 sind die folgenden Anforderungen zu erfüllen:
Es sind Holzwerkstoffe der Holzwerkstoffklasse 100 G zu verwenden.
Fugen sind unter Berücksichtigung der zu erwartenden Längen- und Breitenänderungen infolge Quellens auszubilden. Diese sind in der Regel bei Flachpressplatten mit 2 mm/m und bei Bau-Furniersperrholz mit 1 mm/m zu berücksichtigen.
Die rechtwinklig zu den Auflagern verlaufenden freien Ränder müssen stets miteinander durch Nut und Feder oder gleichwertige Maßnahmen verbunden sein.
Die Dachneigung soll mindestens 2 % betragen. Kleinere Neigungen dürfen nur unter folgenden Bedingungen ausgeführt werden:
14 Kennzeichnung von Voll- und Brettschichtholz
Folgende Bauteile sind dauerhaft, eindeutig und deutlich lesbar zu kennzeichnen:
Als Verbundquerschnitte verleimte tragende Holzbauteile sind auch bei Verwendung von Voll- oder Brettschichtholz der Güteklasse II stets mit dem Herstelltag und dem Zeichen des Herstellwerkes zu kennzeichnen.
| Nachweis der Eignung zum Leimen von tragenden Holzbauteilen | Anhang A |
A.1 Der Nachweis einer bestimmungsgemäßen Herstellung nach Abschnitt 12.1 gilt als erbracht, wenn der Betrieb eine Bescheinigung nach Abschnitt A.3 über seine Eignung zum Leimen von tragenden Holzbauteilen vorlegt.
A.2 Die Bescheinigung wird von Prüfstellen, die dafür anerkannt und in einem Verzeichnis des Instituts für Bautechnik geführt werden, ausgestellt, wenn nach Überprüfung der verantwortlichen Fachkräfte und der Werkseinrichtungen die Eignung des Betriebes festgestellt ist. Die Bescheinigung wird für fünf Jahre widerruflich erteilt. Auf Antrag kann die Geltungsdauer der Bescheinigung um jeweils fünf Jahre verlängert werden. Vor jeder Verlängerung ist eine weitere Betriebsprüfung durchzuführen. Der Inhaber der Bescheinigung muss jeden Wechsel der verantwortlichen Fachkräfte sowie Änderungen wesentlicher Teile der Werkseinrichtungen oder des Leimverfahrens der Prüfstelle anzeigen.
A.3 Die Bescheinigung wird für folgende Gruppen erteilt:
In den Bescheinigungen A, B, C oder D ist außerdem anzugeben, wenn der Betrieb auch den Nachweis für die Herstellung von Keilzinkenverbindungen nach Abschnitt 12.3 erbracht hat.
| Zitierte Normen und andere Unterlagen |
| DIN 96 | Halbrund- Holzschrauben mit Schlitz |
| DIN 97 | Senk-Holzschrauben mit Schlitz |
| DIN 571 | Sechskant-Holzschrauben |
| DIN 1052 Teil 2 | Holzbauwerke; Mechanische Verbindungen |
| DIN 1052 Teil 3 | Holzbauwerke; Holzhäuser in Tafelbauart, Berechnung und Ausführung |
| DIN 1055 Teil 3 | Lastannahmen für Bauten; Verkehrslasten |
| DIN 1055 Teil 4 | Lastannahmen für Bauten; Verkehrslasten, Windlasten bei nicht schwingungsanfälligen Bauwerken |
| DIN 1055 Teil 5 | Lastannahmen für Bauten; Verkehrslasten, Schneelast und Eislast |
| DIN 1074 | Holzbrücken; Berechnung und Ausführung |
| DIN 4074 Teil 1 | Bauholz für Holzbauteile; Gütebedingungen für Bauschnittholz (Nadelholz) |
| DIN 4074 Teil 2 | Bauholz für Holzbauteile; Gütebedingungen für Baurundholz (Nadelholz) |
| DIN 4112 | Fliegende Bauten; Richtlinien für Bemessung und Ausführung |
| DIN 4113 Teil 1 | Aluminiumkonstruktionen unter vorwiegend ruhender Belastung; Berechnung und bauliche Durchbildung |
| DIN 4149 Teil 1 | Bauten in deutschen Erdbebengebieten; Lastannahmen, Bemessung und Ausführung üblicher Hochbauten |
| DIN 4420 Teil 1 | Arbeits- und Schutzgerüste (ausgenommen Leitergerüste); Berechnung und bauliche Durchbildung |
| DIN 4420 Teil 2 | Arbeits- und Schutzgerüste; Leitergerüste |
| DIN 4421 | Traggerüste; Berechnung, Konstruktion und Ausführung |
| DIN 18 800 Teil 7 | Stahlbauten; Herstellen, Eignungsnachweise zum Schweißen |
| DIN 50 049 | Bescheinigungen über Materialprüfungen |
| DIN 52 183 | Prüfung von Holz; Bestimmung des Feuchtigkeitsgehaltes |
| DIN 55 928 Teil 1 | Korrosionsschutz von Stahlbauten durch Beschichtungen und Überzüge; Allgemeines |
| DIN 55 928 Teil 2 | Korrosionsschutz von Stahlbauten durch Beschichtungen und Überzüge; Korrosionsschutzgerechten Gestaltung |
| DIN 55 928 Teil 4 | Korrosionsschutz von Stahlbauten durch Beschichtungen und Überzüge; Vorbereitung und Prüfung der Oberflächen |
| DIN 55 928 Teil 5 | Korrosionsschutz von Stahlbauten durch Beschichtungen und Überzüge; Beschichtungsstoffe und Schutzsysteme |
| DIN 55 928 Teil 6 | Korrosionsschutz von Stahlbauten durch Beschichtungen und Überzüge; Ausführung und Überwachung der Korrosionsschutzarbeiten |
| DIN 55 928 Teil 8 | Korrosionsschutz von Stahlbauten durch Beschichtungen und Überzüge; Korrosionsschutz von tragenden dünnwandigen Bauteilen (Stahlleichtbau) |
| DIN 68 140 | Keilzinkenverbindung von Holz |
| DIN 68 141 | Holzverbindungen; Prüfung von Leimen und Leimverbindungen für tragende Holzbauteile, Gütebedingungen |
| DIN 68 705 Teil 3 | Sperrholz; Bau-Furniersperrholz |
| DIN 68 705 Teil 5 | Sperrholz; Bau-Furniersperrholz aus Buche |
| DIN 68 705 Teil 5 Beiblatt 1 zu DIN 68 705 Teil 5 | Bau-Furniersperrholz aus Buche; Zusammenhänge zwischen Plattenaufbau, elastischen Eigenschaften und Festigkeiten |
| DIN 68 754 Teil 1 | Harte und mittelharte Holzfaserplatten für das Bauwesen; Holzwerkstoffklasse 20 |
| DIN 68 763 | Spanplatten; Flachpressplatten für das Bauwesen, Begriffe, Eigenschaften, Prüfung, Überwachung |
| DIN 68 800 Teil 2 | Holzschutz im Hochbau; Vorbeugende bauliche Maßnahmen |
| DIN 68 800 Teil 3 | Holzschutz im Hochbau; Vorbeugender chemischer Schutz von Vollholz |
Frühere Ausgaben
DIN 1052: 05.38, 07.33, 10.40X 10.47, 08.65
DIN 1052 Teil 1: 10.69
Erläuterungen
Die in dieser Norm verwendeten Formelzeichen weichen teilweise von den in DIN 1080 Teil 5/03.80 festgelegten Formelzeichen ab. Es ist daher vorgesehen, DIN 1080 Teil 5 zu überarbeiten.
Internationale Patentklassifikation
| B 27 N 3/00 |
| B 27 G 11/00 |
| B 27 M 3/00 |
| E 04 B 1/10 |
| E 04 B 1/26 |
| E 04 G 1/02 |
| E 04 G 11/48 |
ENDE