umwelt-online: VDI 3673 - Druckentlastung von Staubexplosionen (3)
 | zurück |  |
Staubexplosionen in Rohrleitungen können sich im Vergleich zu Behälterexplosionen wesentlich heftiger entwickeln. Mit zunehmender Rohrlänge muß mit Detonatidnen mit Flammengeschwindigkeiten bis zu 2000 m × s-1 und kurzzeitigen lokalen Druckspitzen von mehr als 20 bar gerechnet werden. Das Entstehen von Detonationen ist abhängig vom Rohrdurchmesser und von der Staubkonzentration und um so wahrscheinlicher, je höher der KSt- Wert eines Staubes ist. An Endflanschen, Verengungen und Bögen können durch Vorkompression kurzzeitig noch höhere Drücke auftreten. Rohrleitungen, die nach PN 10 gebaut sind, halten vorgenannten Belastungen jedoch stand [5].
Damit im Explosionsfall in Rohrleitungen vergleichbare reduzierte Druckwerte wie bei der Behälterdruckentlastung erreicht werden, müssen Rohrleitungen je nach Geometrie und Festigkeit abschnittsweise radial entlastet werden. Dies ist wegen des Flammenaustritts nur bei Freianlagen möglich (Bild 17).
Bild 17. Explosionsdruckentlastete Rohrleitung (links) bei einer Holzstaubexplosion (rechts)

Wenn eine Rohrleitung in axialer Richtung entlastet wird, können hierdurch Vorkompressionseffekte an Endflanschen vermieden werden. Die Entlastung muß dann aber über den vollen Rohrquerschnitt erfolgen.
Als Druckentlastungseinrichtungen können sowohl Berstscheiben als auch Explosionsklappen verwendet werden.
12 Hybride Gemische
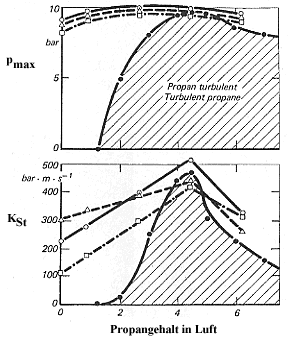
Unter hybriden Gemischen ist das gleichzeitige Auftreten von aufgewirbeltem brennbarem Staub und Brenngasen (z.B. Lösungsmitteldämpfe und brennbare Nebel) zu verstehen. Auch aufgrund ihrer Konzentrationsverhältnisse können sich nicht explosionsfähige Staub/Luft- und nicht explosionsfähige Brenngas/Luft-Gemische zu explosionsfähigen hybriden Gemischen addieren [1; 27]. Bild 18 zeigt für geschlossene Behälter den Zusammenhang zwischen
den Explosionskenngrößen brennbarer Stäube und z.B. dem Propangehalt in der Verbrennungsatmosphäre. Demnach verändert Brenngaszusatz den maximalen Explosionsüberdruck pmax nur unwesentlich. Die staubspezifische Kenngröße KSt unterliegt dagegen einem starken Einfluß: Sie wird mit zunehmendem Brenngasgehalt angehoben (Einstufung in eine höhere Staubexplosionsklasse möglich), erreicht die Explosionskenngröße des Brenngases und fällt erst oberhalb der stöchiometrischen Brenngaskonzentration wieder ab.
Bild 18. Einfluß des Propangehaltes in der Verbrennungsluft auf die Explosionskenngrößen brennbarer Stäube im geschlossenen Behälter (V=1 m3)
 | Δ | optischer Aufheller | |
| o | Zellulose | ||
| ζ[] | Erbsenmehl |
Für die Dimensionierung des Flächenbedarfs bei hybriden Gemischen aus brennbaren Stäuben der Staubexplosionsklassen St 1 und St 2 mit Brenngasen und brennbaren Dämpfen, die ein dem Propan ähnliches Explosionsverhalten haben, ist daher in der Gleichung (3) für homogene Gemische (siehe Abschnitt 6.1.1)
- der maximale Explosionsüberdruck pmax =10 bar,
- die staubspezif. Kenngröße KSt = 500 bar × m × s-1 zu setzen [1].
Gegebenenfalls sind die Explosionskenngrößen des betreffenden hybriden Gemisches zu bestimmen.
Bei hybriden Gemischen mit brennbaren Stäuben der Staubexplosionsklasse St 3 (KSt > 300 bar × m × s-1) in Gegenwart von Brenngasen ist der Rat von Fachleuten einzuholen.
13 Instandhaltung
Druckentlastungseinrichtungen unterliegen einer Reihe von Einflüssen, die ihre Funktion so weit beeinträchtigen können, daß mit Ausfall der Schutzwirkung oder mit unbeabsichtigtem Ansprechen gerechnet werden muß. Druckentlastungseinrichtungen müssen deshalb in angemessenen Abständen überprüft, gewartet und gegebenenfalls instand gesetzt werden.
Berstscheiben können durch Korrosion, Druckwechselbeanspruchung, mechanische Materialabtragung und Alterung geschwächt werden. Explosionsklappen können ebenfalls durch Korrosion und Materialabtragung in ihrer Funktion beeinträchtigt werden. Gravierender ist hier jedoch im allgemeinen die Beeinträchtigung der Funktionssicherheit durch nicht sachgemäß durchgeführte Wartungsarbeiten (z.B. Verkleben durch Anstriche). Eine regelmäßige Inspektion ist notwendig. Explosionsklappen müssen nach dem Ansprechen im Explosionsfall auf weitere Verwendbarkeit überprüft werden.
Für die Wartung von Druckentlastungseinrichtungen anderer Bauart (z.B. Knickstab-Berstsicherungen, Scheiben in Klemmprofilen) ist die Stellungnahme des jeweiligen Herstellers bzw. von Fachleuten einzuholen.
14 Berechnungsbeispiele
In den folgenden Beispielen werden die empirischen Berechnungsgleichungen des Abschnittes 6 für die Explosionsdruckentlastung homogener und inhomogener Staub/Luft-Gemische in Behältern und Silos angewendet. Die Berechnungen wurden zur besseren Nachvollziehbarkeit auf zwei Stellen nach dem Komma durchgeführt, grundsätzlich ist jedoch bei der praktischen Anwendung der Gleichungen eine Aufrundung auf eine Stelle nach dem Komma zu empfehlen. Gegebenenfalls notwendige explosionstechnische Entkopplungsmaßnahmen [1; 7] wurden nicht berücksichtigt.
14.1 Einfluß der Behälterfestigkeit
auf die Entlastungsfläche bei homogener Staubverteilung in kubischen Behältern Für die Berechnung der mit einer Berstscheibe verschlossenen Entlastungsfläche A eines kubischen 20-m3-Behälters (Höhen/Durchmesser-Verhältnis H/D < 2) ohne Einbauten gilt die in Abschnitt 6.1.1 angegebene Basisgleichung (3) für homogene Staub/ Luft-Gemische. Bei vorhandenen Einbauten (z.B. Filter) ist der Berechnung das freie Volumen (Leervolumen minus Hüllvolumen der Filterelemente) zugrunde zu legen und darauf zu achten, daß durch sie der Explosionsdruckentlastungsvorgang nicht behindert wird.
Für die Staubexplosionsklasse St 1, einen maximalen Explosionsüberdruck von pmax = 9 bar und einen statischen Ansprechüberdruck der Berstscheibe von pstat = 0,1 bar errechnen sich für verschiedene Behälterfestigkeiten p folgende Entlastungsflächen A:
| V = 20 m3: pmax = 9 bar, KSt = 200 bar × m × s-1, pstat = 0.1 bar | |
| p = pred,max in bar | A in m |
| 0.25 | 1.23 |
| 0.50 | 0.83 |
| 1.00 | 0.56 |
14.2 Einfluß von Explosionsklappen bei homogener Staubverteilung in kubischen Behältern
14.2.1 Erhöhung der Behälterfestigkeit
Bei Anwendung einer Explosionsklappe (siehe Abschnitt 5.2) mit einem statischen Ansprechüberdruck von pstat = 0,1 bar gilt für die Erhöhung der Behälterfestigkeit Von p = pred,max auf p = pred,max gemäß Prüfbericht:
| p = 1.155× p | 0.8635 | in bar |
| red,max |
| V = 20 m3: pmax = 9 bar, KSt = 200 bar × m × s-1, pstat = 0.1 bar | ||
| p = pred,max in bar | A in m2 | p = pred,max in bar |
| 0.25 | 1.23 | 1.42 |
| 0.50 | 0.83 | 0.92 |
| 1.00 | 0.56 | 1.15 |
14.2.2 Erhöhung des Flächenbedarfs
Für die Entlastungsfähigkeit (Bild 6) gilt für die gleiche Explosionsklappe (s.o.) gemäß Prüfbericht:
| EF = 93.8 × p | 0.05575 | in % |
| red,max |
Die vergrößerte Entlastungsfläche A* ist der folgenden Tabelle zu entnehmen:
| V = 20 m3: pmax = 9 bar, KSt = 200 bar × m × s-1, pstat = 0.1 bar | |||
| p = pred,max in bar | A in m2 | EF in % | A* in m2 |
| 0.25 | 1.23 | 86.8 | 1.42 |
| 0.50 | 0.83 | 90.2 | 0.92 |
| 1.00 | 0.56 | 93.8 | 0.60 |
A* erforderliche Explosionsklappenfläche beim Einsatz einer Explosionsklappe mit der Entlastungsfähigkeit
14.3 Einfluß von Abblasrohren bei homogener Staubverteilung in kubischen Behältern
14.3.1 Erhöhung der Behälterfestigkeit
Werden Berstscheiben Abblasrohre nachgesetzt, ist - wie bei Explosionsklappen - die Behälterfestigkeit p auf pred,max gemäß Gleichungen (19) und (20) (Abschnitt 10.1) wie folgt zu erhöhen.
| V = 20 m3: pmax = 9 bar, KSt = 200 bar × m × s-1, pstat = 0.1 bar | |||
| Abblasrohrlänge l | 0 m < l < 3 m | 3 m < l < 6 m | |
| pred,max in bar | A in m2 | p = p´red,max in bar | p = p´red,max in bar |
| 0.25 | 1.23 | 0.74 | 1.55 |
| 0.50 | 0.83 | 1.17 | 2.15 |
| 1.00 | 0.56 | 1.84 | 3.00 |
14.3.2 Erhöhung des Flächenbedarfs
Werden Berstscheiben Abblasrohre nachgesetzt, so ist bei vorgegebener Behälterfestigkeit p die Entlastungsfläche mit Hilfe der Gleichungen (21) und (22) (Abschnitt 10.1) in Verbindung mit Gleichung (3) (Abschnitt 6.1.1) wie folgt von A auf A* zu vergrößern:
| V = 20 m3: pmax = 9 bar, KSt = 200 bar × m × s-1, pstat = 0.1 bar | |||||
| Abblasrohrlänge l | 0 m < l < 3 m | 3 m < l < 6 m | |||
| pred,max in bar | A in m2 | pred,max in bar | A* in m2 | pred,max in bar | A* in m2 |
| 0.25 | 1.23 | < 0.10 | unzulässig | < 0.1 | |
| 0.50 | 0.83 | 0.14 | 1.72 | < 0.1 | unzulässig |
| 1.00 | 0.56 | 0.39 | 0.96 | 0.1 | 2.08 |
| 1.25 | 0.49 | 0.55 | 0.79 | 0.16 | 1.59 |
A* erforderliche Entlastungsfläche mit Abblasrohr
Im vorgegebenen Anwendungsfall muß daher die Behälterfestigkeit für kurze Abblasrohre mindestens 0,5 bar und für lange Abblasrohre mindestens 1 bar betragen.
14.4 Inhomogene Staubverteilung in kubischen Behältern
Bei Anwendung der Basisgleichung (4) (Abschnitt 6.1.2) wird nach dem gleichen Verfahren der Flächenbedarf für inhomogene Staub/Luft-Gemische der Staubexplosionsklassen St 1 und St 2 in kubischen Behältern gegebenenfalls unter Berücksichtigung eines Explosionsklappeneinflusses auf die Behälterfestigkeit und den Flächenmehrbedarf berechnet. Sind Abblasrohre vorhanden, so sind die Angaben von Bild 16 zu berücksichtigen.
14.5 Flächenbedarf von Silos
14.5.1 Homogene Staubverteilung
Die Entlastungsfläche AL für Silos mit einem Höhen/ Durchmesser-Verhältnis von H/D > 2 wird mit Hilfe der Basisgleichung (3) (Abschnitt 6.1.1) in Verbindung mit Gleichung (7) (Abschnitt 6.2.1) für ein konstantes Volumen wie folgt berechnet
| V = 100 m3: pmax = 9 bar, KSt = 200 bar × m × s-1, pstat = 0.1 bar | ||||
| H/D | pred,max in bar | A in m2 | ΔAH in m2 | AL in m2 |
| 2 | 0.25 | 4.15 | 4.18 | 8.33 |
| 0.50 | 2.79 | 1.73 | 4.52 | |
| 1.00 | 1.88 | 0.43 | 2.31 | |
| 3 | 0.25 | 4.15 | 6.63 | 10.78 |
| 0.50 | 2.79 | 2.73 | 5.52 | |
| 1.00 | 1.88 | 0.68 | 2.56 | |
| 4 | 0.25 | 4.15 | 8.37 | 12.52 |
| 0.50 | 2.79 | 3.45 | 6.24 | |
| 1.00 | 1.88 | 0.86 | 2.74 | |
| 5 | 0.25 | 4.15 | 9.72 | 13.87 |
| 0.50 | 2.79 | 4.01 | 6.80 | |
| 1.00 | 1.88 | 1.00 | 2.88 | |
14.5.2 Inhomogene Staubverteilung
Die Entlastungsfläche AL für Silos mit einer Höhe H510 m errechnet sich nach der Basisgleichung (4) (Abschnitt 6.1.2) und mit einer Höhe von H > 10 m nach der Basisgleichung (8) (Abschnitt 6.2.2) in Verbindung mit der Gleichung (9) (Abschnitt 6.2.2) für ein konstantes Volumen wie folgt:
| V = 100 m3: pmax = 9 bar, KSt = 200 bar × m × s-1, pstat = 0.1 bar, DF = 0.1 m, vF < 40 m × s-1 | |||||
| H/D | H in m | p = pred,max in bar | A in m2 | ΔAI in m2 | AL in m2 |
| 2 | 7.99 | 0.25 | 1.05 | 1.97 | 3.02 |
| 0.50 | 0.80 | 0.62 | 1.42 | ||
| 1.00 | 0.55 | 0.18 | 0.73 | ||
| Wechsel der Basisgleichung | |||||
| 3 | 10.46 | 0.25 | 1.10 | 3.27 | 4.37 |
| 0.50 | 0.84 | 1.04 | 1.88 | ||
| 1.00 | 0.58 | 0.30 | 0.88 | ||
| 4 | 12.68 | 0.25 | 1.34 | 5.03 | 6.37 |
| 0.50 | 1.02 | 1.59 | 2.61 | ||
| 1.00 | 0.70 | 0.45 | 1.15 | ||
| 5 | 14.71 | 0.25 | 1.55 | 6.75 | 8.30 |
| 0.50 | 1.18 | 2.13 | 3.31 | ||
| 1.00 | 0.81 | 0.61 | 1.42 | ||
14.5.3 Silofestigkeiten
Man wird im allgemeinen bemüht sein, die Flächenforderungen für homogene Staubverteilung (Abschnitt 14.5.1) und für inhomogene Staubverteilung (Abschnitt 14.5.2) durch Anordnung der Entlastung auf dem Behälterdach zu erfüllen. Stehen aufgrund des Platzbedarfs für Fördereinrichtungen u.ä. nur zwei Drittel dieser Fläche für die Entlastung zur Verfügung, dann ergeben sich folgende Minimalwerte pmin für die Behälterfestigkeit:
| V = 100 m3: pmax = 9 bar, KSt = 200 bar × m × s-1, pstat = 0.1 bar | ||||||
| Stauverteilung | homogen | inhomogen | ||||
| H/D | D in m | 2/3 Atop in m2 | pmin = pred,max in bar | AL in m2 | pmin = pred,max in bar | AL in m2 |
| 2 | 3.99 | 8.34 | 0.25 | 8.33 | 0.13 | 7.18 |
| 3 | 3.49 | 6.38 | 0.45 | 6.16 | 0.20 | 5.89 |
| 4 | 3.17 | 5.26 | 0.60 | 5.12 | 0.30 | 4.97 |
| 5 | 2.94 | 4.53 | 0.75 | 4.23 | 0.40 | 4.42 |
Homogene Staubgemische erfordern gegenüber inhomogenen eine ungefähr doppelte Behälterfestigkeit.
14.6 Flammenreichweite und Außendruck druckentlasteter kubischer Behälter mit homogener Staubverteilung
In Abschnitt 7 werden Gleichungen (12) bis (15) für die Abschätzung der maximalen Flammenreichweite LF, H des aus der Entlastungsöffnung kubischer Behälter austretenden Flammenstrahls und des maximalen Spitzenüberdruckes pmax,a der entstehenden Sekundärexplosion angegeben. Die folgende Tabelle macht entsprechende Angaben für zwei Volumina und den mit zunehmendem Abstand r sich vermindernden Spitzenüberdruck pr.
| pmax = 9 bar, KSt = 200 bar × m × s-1, pstat = 0.1 bar | ||||||||
| Abstand r von der Entlastungsfläche A in m | 10 | 20 | 30 | |||||
| V in m3 | LF,H in m3 | A in m2 | pmax,a in bar | pmax,a in bar | Rs in m | pr in bar | ||
| 20 | 21.72 | 1.23 | 0.25 | 0.088 | 5.43 | 0.035 | 0.012 | 0.004 |
| 0.83 | 0.50 | 0.168 | 0.067 | 0.024 | 0.008 | |||
| 0.56 | 1.00 | 0,322 | 0.129 | 0.046 | 0.016 | |||
| 60 | 31.32 | 2.83 | 0.25 | 0.116 | 7.83 | 0.080 | 0.028 | 0.010 |
| 1.90 | 0.50 | 0.223 | 0.154 | 0.055 | 0.019 | |||
| 1.28 | 1.00 | 0.428 | 0.297 | 0.105 | 0.037 | |||
14.7 Rückstoßkräfte
Die folgende Tabelle macht für zwei nach oben explosionsdruckentlastete Behälter Angaben über die auf die stützende Baukonstruktion wirkende maximale Rückstoßkraft FR,max, die Rückstoßdauer tD (Gl. (17)) und den übertragenden Gesamtimpuls I (Gl. (18)) für homogene Staubverteilung der Staubexplosionsklasse St 1.
| pmax = 9 bar, KSt = 200 bar m × s-1, pstat = 0.1 bar | |||||
| V in m3 | A in m2 | pmax,a in bar | FR,max in kN | tD in s | I in kN × s |
| 20 | 1.23 | 0.25 | 36.59 | 1.30 | 24.75 |
| 0.83 | 0.50 | 49.39 | 0.96 | 24.75 | |
| 0.56 | 1.00 | 66.64 | 0.71 | 24.75 | |
| 30 | 2.82 | 0.25 | 83.90 | 1.70 | 74.26 |
| 1.90 | 0.50 | 113.05 | 1.26 | 74.26 | |
| 1.28 | 1.00 | 152.32 | 0.94 | 74.26 | |
Schrifttum
[1] Bartknecht, W.: Explosionsschutz: Grundlagen und Anwendung. Berlin, Heidelberg, New York: Springer 1993
[2] VDI 2263 Staubbrände und Staubexplosionen; Gefahren - Beurteilung - Schutzmaßnahmen
[3] Verordnung über gefährliche Stoffe (GefahrstoffverordnungGefStoffV) vom 26.08.1986 (BGBl. I S. 1470) in der jeweils aktuellen Fassung
[4] AD-Merkblätter: Richtlinie für Werkstoffe; Berechnung, Herstellung und Ausrüstung von Druckbehältern. Köln: Karl Heymanns Verlag
[5] VDI2263 Blatt 3 Staubbrände und Staubexplosionen; Gefahren - Beurteilung - Schutzmaßnahmen; Explosionsdruckstoßfeste Behälter und Apparate; Berechnung, Bau und Prüfung
[6] ISO 6184-1 Explosion protection systems - Part 1: Determination of explosion indices of combustible dusts in air. International Organisation for Standardization, 1985
[7] VDI 2263 Blatt 1 Staubbrände und Staubexplosionen; Gefahren, Beurteilung Schutzmaßnahmen; Untersuchungsmethoden zur Ermittlung von sicherheitstechnischen Kenngrößer von Stäuben
[8] Siwek, R., u. 0. Skov: Modellberechnung zur Dimensionierung von Explosionsklappen auf der Basis von praxisnahen Explosionsversuchen. VDI-Berichte 701, S. 569/616. Düsseldorf: VDI-Verlag 1989
[9] Wemann, W., R. Bauer u. F. Möller: Unterdruck-Sicherungen von Silos nach Staubexplosionen bei Anwendung von Explosionsklappen. VDI-Berichte 701, S. 775/800. Düsseldorf: VDI-Verlag 1989
[10] Bartknecht, W.: Maßnahmen gegen gefährliche Auswirkungen von Staubexplosionen in Silos und Behältern: Explosionsdruckentlastung beim Befüllen durch Flugförderung. VDI Fortschrittberichte, Reihe 3, Verfahrenstechnik Nr. 182. Düsseldorf: VDI-Verlag 1989
[11] Siwek, R.: Druckentlastung von Staubexplosionen beim pneumatischen Befüllen von Behältern. VDI-Berichte 701, S. 529/567. Düsseldorf: VDI-Verlag 1989
[12] Eckhoff, R.K.: Dust explosions in the process industries. Chapter 6. Oxford: Butterworth-Heinemann 1991
[13] Wrkner-Bott, I., St. Schumann u. M. Stock: Dust explosion venting: Investigation of the secondary explosion. 7th International Symposium an Loss Prevention and Safety Promotion in the Process Industries, Taormina, Italy, 4-8 May 1992 (Vol. 4, Paper No. 58)
[14] NFPA 68 Venting of Deflagrations. 1978 and 1994 editions, National Fire Protection Ass. Quincy, Massachussets/USA
[15] Wirkner-Bott, I., St. Schumann u. M. Stock: Flammen und Druckwirkung bei Explosionsdruckentlastung. VDI-Berichte 975, S. 285ff. Düsseldorf: VDI-Verlag 1992
[16] Faber, M., u. F. Afert: Verhinderung der Flammenausbreitung von Staubexplosionen aus explosionsdruckentlasteten Apparaten - Quench-Rohr-Systeme. VDI-Berichte 975, S. 447/456. Düsseldorf: VDI-Verlag 1992
[17] Yogi, A., u. W. Bartknecht: Verhinderung der Flammenausbreitung von Staubexplosionen aus explosionsdruckentlasteten Apparaturen durch Bandsicherungen: VDI-Berichte 975, S. 457/479. Düsseldorf: VDI-Verlag 1992
[18] Faber, M.: Rückstoßkräfte bei der Explosionsdruckentlastung. Zement-Kalk-Gips 36 (1983) 9,'S. 531/534
[19] Hattwig, M., u. M. Faber: Rückstoßkräfte bei der Explosionsdruckentlastung. VDI-Berichte 494, S. 219/226. Düsseldorf. VDI-Verlag 1984
[20] Brunner, M.Y.: Bauwerksbeanspruchungen durch die Rückstoßkräfte druckentlasteter Staubexplosionen in BehäItem. Diss. ETH Zürich, Nr. 7223, 1983; VDI-Berichte 494, S. 227/232. Düsseldorf: VDI-Verlag 1984
[21] Faber, M.: Explosionsdruckentlastung als Schutzmaßnahme führt zu Rückstoßkräften. Maschinenmarkt 91 (1985) 16, 5.272/275
[22] Faber, M.: Recoil forces of vented explosions in technical installations. EuropEx News Letter, Dec. 1991, S. 2/3
[23] Harmany, A.: Duration of vented dust explosions. Europex Newsletter 12/1993
[24] Siwek, R.: Einfluß von Ausblasrohren,auf die Druckentlastung von Staubexplosionen. Staub, Reinhaltung Luft 49 (1989) 10, S. 327/331
[25] Siwek, R.: Explosionsdruckentlastung - Novellierung der Richtlinie VDI 3673. VDI-Berichte 975, 5.401/431. Düsseldorf: VDI-Verlag 1992
[26] Siwek, R.: New, Revised VDI-Guideline 3673, 28th Annual Loss Prevention Symposium, Atlanta, Georgia, USA, April 17-21,1994
[27] Bartknecht, W.: Untersuchung des Explosions- und Zündverhaltens brennbarer Stäube und hybrider Gemische.
Schriftenreihe "Humanisierung des Arbeitslebens" Band 64, Herausge ber: Der Bundesminister für Forschung und Technologie.
Düsseldorf:
VDI-Verlag 1985
 | ENDE |  |
...
X
⍂
↑
↓
