umwelt-online: VDI 3673 - Druckentlastung von Staubexplosionen (2)
 | zurück |  |
6.1.2 Inhomogene Staubverteilung
Bei axialer, zentraler Einförderung von Produkt durch pneumatischen Transport mittels Flugförderung in kubische Behälter entsteht bis zu Fördergeschwindigkeiten von υF = 40 m × s-1 eine inhomogene Staubverteilung und daher bei einer Staubexplosion ein wesentlich verminderter Druck im entlasteten kubischen Behälter gegenüber einer homogenen Gemischverteilung [10; 11; 12]. Die erforderliche Entlastungsfläche A kann nach der folgenden empirischen Zahlenwertgleichung berechnet werden:
| × | ||
| A = [ 1/DZ (8.6 log pred,max - 6) - 5.5 log pred,max + 3.7] × 0.011 × KSt × DF | in m2 | (4) |
Bild 9. Nomogramm zur Bestimmung der Entlastungsflächen für kubische Behälter bei homogener Staubverteilung (maximaler Explosionsüberdrück pmax = 9 bar, statischer Ansprechüberdruck pstat = 0,1 bar)
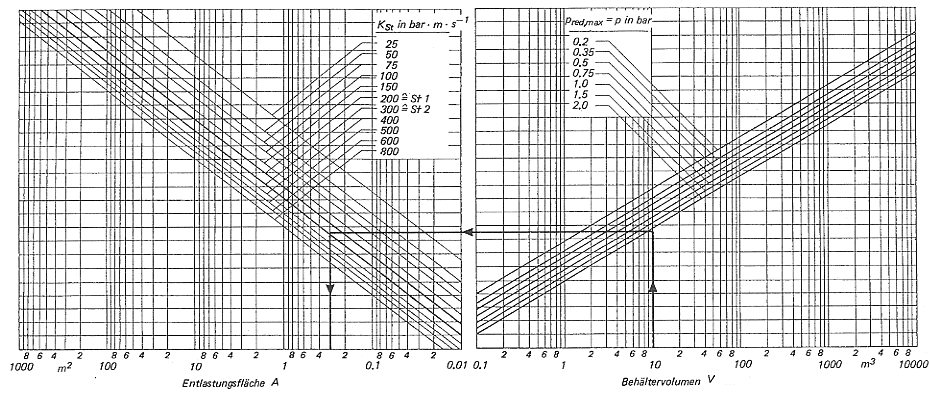
Die Gleichung gilt unabhängig von der Produktbeladung des Förderstromes für
- Volumina 5 m3 < V < 10000 m3
- eine axiale, zentrale Einförderung des Gutstromes über ein Förderrohr vom Durchmesser DF in m bis zu Fördergeschwindigkeiten von υ F = 40 m × s-1 in einen kubischen Behälter ohne Einbauten
- einen Luftvolumenstrom von Q < 2500 m3 × h-1
- einen statischen Ansprechüberdruck der Berstscheibe von pstat < 0,1 bar
- einen maximalen reduzierten Explosionsüberdruck von 0,1 bar < pred,max < 2 bar
- einen maximalen Explosionsüberdruck von 8 bar < pmax < 9 bar
- eine staubspezifische Kenngröße von 50 bar × m × s-1 < s-1 < KSt < 300 bar × m × s-1
Das zu schützende Volumen V ist dem Inhalt eines Zylinders vom Höhen/Durchmesser-Verhältnis = 1 gleichzusetzen, dessen Durchmesser DZ sich aus folgender Gleichung ergibt:
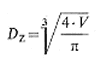 | in m | (5) |
Für den Fall einer vorhandenen Behälterfestigkeit von p > 0,25 bar liefert die Gleichung (4) auch für höhere Luftvolumenströme (jedoch Q < 5000 m3 × h-1) den erforderlichen Flächenbedarf, wenn pred,max = 0,1 bar gesetzt wird [10; 11].
Die Bestimmung der beim pneumatischen Befüllen von kubischen Behältern erforderlichen Entlastungsfläche für die Staubexplosionsklassen St 1 kann nach dem in Bild 10 gezeigten Nomogramm erfolgen.
6.2 Langgestreckte Behälter
Stehende oder liegende langgestreckte Behälter sind dadurch gekennzeichnet, daß die Höhe oder die Länge größer ist als der Durchmesser (äquivalenter Durchmesser). Diese geometrische Eigenschaft bedingt, daß sich mit zunehmender Höhe oder Länge eines Behälters die Flammenausbreitung beschleunigt. Die diesen Einfluß beschreibenden Gleichungen gelten bereits dann, wenn das Verhältnis Höhe (Länge) zu Durchmesser H/D > 1 ist. Für die Praxis ist dies allerdings erst ab H/D > 2 relevant.
Der Flächenbedarf für Druckentlastungsflächen wird dabei mit zunehmendem Verhältnis Höhe (Länge) zu Durchmesser gegenüber dem Flächenbedarf für kubische Behälter größer (Bild 11).
Die prozentuale erforderliche Vergrößerung der Entlastungsfläche gegenüber einem kubischen Behälter
Bild 10. Nomogramm für die Bestimmung der Druckentlastungsflächen für kubische Behälter mit inhomogener Staubverteilung (pneumatisches Befüllen)
- Staubexplosionsklasse St 1 -
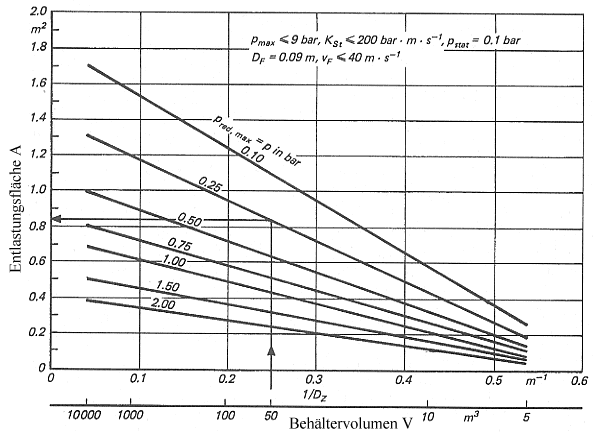
Bild 11. Flächenmehrbedarf ΔAH von langgestreckten Behältern und Silos mit homogenen Staub/Luft-Gemischen in Abhängigkeit vom Höhen/Durchmesser-Verhältnis H/D
mit dem gleichen Volumen hängt außer vom Höhen/ Durchmesser-Verhältnis vom maximalen reduzierten Explosionsüberdruck und von der Art der Staubwolkenbildung ab.
Ist der maximale reduzierte Explosionsüberdruck bei homogenen Staub/Luft-Gemischen pred,max > 1,5 bar und bei inhomogenen Staubluft-Gemischen pred,max > 2 bar, dann ist der Einfuß des Höhen/Durchmesser-Verhältnisses nicht mehr festzustellen, d.h. diese Behälter können wie kubische Behälter betrachtet werden [1].
Die Entlastungsfläche für einen langgestreckten Behälter ergibt sich aus der Entlastungsfläche für den kubischen Behälter und einem Zuschlag. Dabei müssen sich die Rechenoperationen der gleichen Grundparameter bedienen, d. h. der maximale reduzierte Explosionsüberdruck sowie das Füllverfahren müssen bei der Benutzung der Gleichungen für die Berechnung der Entlastungsfläche für den kubischen Behälter und für die Berechnung des Zuschlages identisch sein. Somit ergibt sich für die Entlastungsfläche AL eines langgestreckten Behälters unabhängig von der Befüllungsart bis zu Volumina V = 10000 m3:
| AL = A + ΔA | (6) |
| AL | = Entlastungsfläche für den langgestreckten Behälter |
| A | = Entlastungsfläche für den kubischen Behälter mit dem gleichen Volumen |
| ΔA | = Zuschlag für H/D > 2 |
6.2.1 Homogene Staubverteilung
Für einen langgestreckten Behälter mit homogener Staubverteilung ergibt sich für den Flächenmehrbedarf Δ AH in m2 empirisch aus Versuchsreihen:
| ΔAH = A(-4.305 - log pred,max + 0.758) × log H/D | in m2 | (7) |
Es gelten die für Gleichung (3) angegebenen Bedingungen.
6.2.2 Inhomogene Staubverteilung
Für einen langgestreckten Behälter der Höhe H < 10 m und inhomogene Staubverteilung, wie sie z.B. durch pneumatisches Befüllen oder freien Fall gebildet wird, gilt die in Abschnitt 6.1.2 genannte Basisgleichung (4). Ist seine Höhe H > 10 m, dann ist von folgender Gleichung auszugehen:
| A = [ 1/DZ (8.6 log pred,max - 6) - 5.5 log pred,max + 3.7] × 0.011 × KSt × H × DF | in m2 | (8) |
Bei Befüllung im freien Fall ist die abgeworfene Produktmenge auf M < 8000 kg × h -1 zu begrenzen und für DF der (äquivalente) Durchmesser der Fallöffnung in die Basisgleichungen einzusetzen.
Der sich empirisch aus Versuchsreihen ergebende Flächenmehrbedarf ΔAI beträgt:
| ΔAI = A × 1,0715 p | - 1,27 | × log H/D in m2 (9) |
| red,max |
Ansonsten gelten die für Gleichung (4) angegebenen Bedingungen.
6.2.3 Silos und Bunker
Silos und Bunker sind im allgemeinen gekennzeichnet durch große Volumina und ein Höhen/Durchmesser-Verhältnis von H/D > 2. Sie können einzeln aufgestellt bzw. aufgebaut oder in "Batterien" angeordnet freistehend bzw. in Gebäude integriert sein. Silos und Bunker stehen in der Regel in Verbindung mit Transportsystemen. Die Staubverteilung während des Füllvorganges hängt dabei von der Art des Transportsystems ab. Beim Entleervorgang hängt die Staubverteilung von den Produkteigenschaften (z.B. Neigung zur Brückenbildung) sowie von der Geometrie und den Wandeigenschaften (Staubablagerung) ab.
Für Silos und Bunker mit einem Höhen/Durchmesser-Verhältnis von H/D < 2 kann die Berechnung der Druckentlastungsfläche analog zu den kubischen Behältern durchgeführt werden, für solche mit H/D > 2 ist die Berechnung wie bei den langgestreckten Behältern vorzunehmen.
Bei einem maximalen reduzierten Explosionsüberdruck von pred,max > 1,5 bar (homogene Staub/Luft-Gemische) bzw. von pred,max > 2 bar (inhomogene Staub/Luft-Gemische) ist der Einfluß des H/D-Verhältnisses insbesondere bei Kleinsilos nicht mehr festzustellen [1]. Sie können dann wie kubische Behälter behandelt werden.
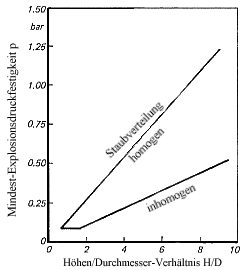
Bild 12. Minimale Explosionsdruckfestigkeit p eines 500-m3-Silos als Funktion des Höhen/Durchmesser-Verhältnisses H/D
pmax = 9 bar, KSt = 200 bar × m × s-1
75% des Daches als Entlastungsfläche ausgebildet: pstat
= 0,1 bar
Man beachte, daß für Silos aufgrund der baulichen Vorgaben in vielen Fällen die Explosionsdruckentlastung nur über die Silodecke erfolgen kann und aufgrund des Platzbedarfs für Fördereinrichtungen u. ä. im allgemeinen nicht einmal der gesamte Querschnitt für die Entlastung zur Verfügung steht. Je größer das H/D-Verhältnis ist, desto höher muß die Explosionsdruckfestigkeit des Silos sein (Bild 12). Wird das Silo für einen Überdruck von 1,5 bar ausgelegt, dann reicht der Entlastungsquerschnitt für alle in Bild 11 angegebenen H/D-Verhältnisse aus.
Wird bei Silos eine seitliche Entlastung vorgesehen, so müssen besonders Rückstoßkräfte berücksichtigt werden (siehe Abschnitt 8).
Bei Silos, die vertikal, d.h. über die Decke durch ein Abblasrohr (l < 6 m) entlastet werden, vermindert sich mit zunehmendem H/D-Verhältnis der Einfluß auf den maximalen reduzierten Explosionsüberdruck. Ist dieses Verhältnis H/D < 2, ist die Erhöhung des maximalen reduzierten Explosionsüberdruckes am größten, und es gilt uneingeschränkt der Inhalt des Abschnittes 10. Ist H/D > 6, wird für Silofestigkeiten p > 0,5 bar der maximale reduzierte Explosionsüberdruck nicht sicherheitsrelevant erhöht. Bestehen Schwierigkeiten bei der Bemessung der Silofestigkeit in Abhängigkeit vom Höhen/Durchmesser-Verhältnis, sind Fachleute zu Rate zu ziehen.
Müssen Silozellen in "Wetterschutzräume" (nicht Betriebsräume), z.B. Siloböden, entlastet werden, so müssen diese Räume entweder explosionsdruckentlastet sein oder es muß eine Explosionsübertragung verhindert werden.
6.2.4 Entlastung von rechteckigen Räumen
Müssen rechteckige Räume (Volumen V) mit Staubanfall wie Silokeller, Verbindungsgänge, Treppenhäuser explosionsdruckentlastet werden, können die notwendigen Entlastungsflächen nach Angaben der Zahlenwertgleichungen für homogene Staubverteilung berechnet werden.
Der Bemessungsüberdruck pBem der tragenden und raumabschließenden Bauteile eines Explosionsabschnittes liegt im allgemeinen zwischen 0,02 bar und 0,1 bar. In diesem Fall geht die Basisgleichung (3) für kubische Behälter über in:
| A = (3.264 × 10-5 × pmax × KSt × p | - 0.569 | ) × V0.753 in m2 (10) |
| Bem |
d.h. pred,max wird gleich pBem und pstat = const =0,1 bar gesetzt.
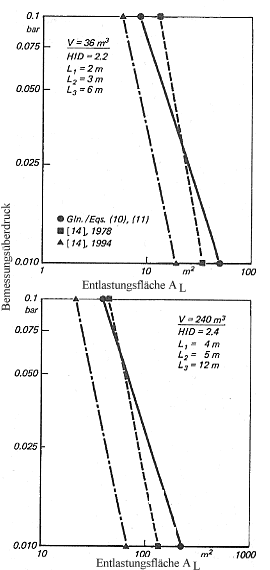
Bild 13. Flächenbedarf bei Druckentlastung von rechteckigen Räumen mit homogener Staubverteilung in Abhängigkeit vom Bemessungsüberdruck pBem
- Staubexplosionsklasse St 1 -
Für langgestreckte Räume mit einem Längen/Durchmesser-Verhältnis L3/DE > 2 ist die Gleichung (7) für den Flächenmehrbedarf wie folgt zu ändern:
ΔAH = A (- 4.305 log pBem + 0.758) log L3/DE in m2 (11)
wobei L3 die größte Lineardimension und
DE = 2 (L1 × L2 /π)0,5 in m
ist. Bild 13 zeigt den Flächenbedarf für Stäube der Staubexplosionsklasse St 1 im Vergleich zu anderen Berechnungsgleichungen [14].
7 Gefahren durch Flammen und Druck
Explosionsdruckentlastung ist immer mit Flammenausbreitung (siehe Abschnitt 10 sowie die Bilder 5 und 13) und Druckwirkungen im Außenraum verbunden. Ursache hierfür ist der Ausschub von unverbranntem Produkt in den Außenraum nach dem Ansprechen der Entlastungseinrichtung mit anschließender Entzündung, des im Außenraum entstehenden Staub/Luft-Gemisches durch den aus der Entlastungsöffnung austretenden Flammenstrahl. Die Flammenausdehnung ist um so größer, je niedriger der statische Ansprechüberdruck und je kleiner die Entlastungsfläche ist; sie kann in Abhängigkeit vom Volumen des druckentlasteten Behälters Längen von über 50 m erreichen.
Durch die Entlastungsvorgänge dürfen Personen nicht gefährdet und die Wirksamkeit von sicherheitstechnisch bedeutsamen Anlagenteilen nicht beeinträchtigt werden. Dies ist bereits bei der Planung von Anlagen zu berücksichtigen und kann häufig dadurch erreicht werden, daß die Druckentlastung nach oben erfolgt (Bild 14).
Ist dies nicht möglich, sollten die Druckentlastungsöffnungen so hoch wie möglich an der Seite des Behälters angebracht sein. Wegen der. Gefahr des Staubauswurfes ist darauf zu achten, daß die Oberfläche der Staubschüttung bei dem .maximal unter Betriebsbedingungen möglichen Füllungsgrad des Behälters die Unterkanten der Druckentlastungsöffnungen nicht erreicht.
Bild 14. Staubexplosion in einem nach oben explosionsdruckentlasteten 250-m3-Behälter bei homogener Staubverteilung

7.1 Anlagen im Freien
Bei Anlagen im Freien ist darauf zu achten, daß für die Umgebung keine Gefährdung durch Flammenaustritt und Druck entsteht. Brennbare Materialien (z.B. Dachabdeckungen) sollen in der Umgebung von Abblasöffnungen nicht vorhanden sein.
7.1.1 Flammenausbreitung
Die maximale Reichweite LF, H der bei Explosionen homogener Staub/Luft-Gemische aus einem Behälter in den Außenraum austretenden Flammen erhöht sich mit zunehmendem entlastetem kubischem Leervolumen nach der empirischen Gleichung
| LF,H = 8 × V1/3 | in m | (12) |
Für Stäube der Staubexplosionsklasse St 2 sind gegenüber Stäuben der Staubexplosionsklasse St 1 etwas geringere Flammenreichweiten zu erwarten. Die Gleichung gilt für
- Volumina 0,3 m3 < V < 10.000 m3,
- einen statischen Ansprechüberdruck der Berstscheibe von pstat < 0,1 bar,
- einen maximalen reduzierten Explosionsüberdruck von pred,max < 1 bar,
- einen maximalen Explosionsüberdruck von pmax < 9 bar,
- eine staubspezifische Kenngröße von 200 bar × m × s-1 < KSt < 300 bar × m × s-1.
Die maximale Flammenreichweite LF,I der bei Explosionen inhomogener Staub/Luft-Gemische im Behälter in den Außenraum austretenden Flammen vermindert sich mit zunehmendem entlastetem kubischem Leervolumen nach der empirischen Gleichung
| LF,I = 15 × V-0.25 | in m | (13) |
Die Gleichung gilt für Volumina 10 m3 < V < 10.000 m3 unter den sonst gleichen Bedingungen wie für Gleichung (12) angegeben.
Ursache hierfür ist die deutlich herabgesetzte Explosionsheftigkeit solcher Gemische, die beim pneumatischen Befüllen entstehen, gegenüber homogenen Staub/Luft-Gemischen. Bei langgestreckten Behältern mit einem Höhen/Durchmesser-Verhältnis von H/D > 2 sind größere Flammenlängen zu erwarten.
7.1.2 Druckwirkung
Über die Druckwirkung von Staubexplosionen außerhalb kubischer Behälter im Bereich der Entlastungsfläche können zur Zeit nur richtungweisende Angaben gemacht werden [13; 14]. Der zeitliche Druckverlauf ist gekennzeichnet durch zwei Druckmaxima, hervorgerufen durch den Entlastungsvorgang selbst (Primärexplosion) und die nachfolgende Entzündung des außen entstandenen Staub/Luft-Gemisches (Sekundärexplosion). Sie werden sowohl von der staubspezifischen Kenngröße KSt, als auch von der Zündortlage im Behälter beeinflußt. Nach dem augenblicklichen Erkenntnisstand kann für homogene Staub/Luft-Gemische in kubischen, Behältern, die über Berstscheiben entlastet werden, der maximal auftretende Spitzenüberdruck pmax, a wie folgt abgeschätzt werden
pmax, a = 0.2 × pred,max × A0.1 × V0.18 in bar (14)
Dieser Druck tritt in einem Abstand von RS = 0,25 × LF, H von der Entlastungsfläche auf. Für größere Abstände r vermindert sich der Spitzenüberdruck pr nach der Gleichung
pr = pmax, a × (RS/r)1.5 (15)
Die Gleichungen gelten für
- Volumina 0,3 m3 < V< 10000 m3,
- einen statischen Ansprechüberdruck der Berstscheibe von pstat < 0,1 bar,
- einen maximalen reduzierten Explosionsüberdruck von pred,max < 1 bar,
- einen maximalen Explosionsüberdruck von pmax < 9 bar,
- eine staubspezifische Kenngröße von KSt < 200 bar × m × s -1.
7.2 Anlagen in geschlossenen Räumen
Wird die Druckentlastung bei Apparaturen in geschlossenen Räumen angewandt, so ist es zum Schutz der Räume und der darin Beschäftigten notwendig, die Druckentlastung über eine Rohrleitung (sogenanntes Abblasrohr) in ungefährliche Richtung ins Freie zu führen (siehe Abschnitt 10).
Neue Entwicklungen zeigen, daß der Flammenaustritt aus explosionsdruckentlasteten Apparaturen unter bestimmten Bedingungen durch geprüfte Entkopplungseinrichtungen [5], z.B. mechanische Flammensperren (Bandsicherung, Quenchvorrichtungen mit Staubrückhaltung) [16; 17], sicher unterbunden werden kann.
8 Berücksichtigung von Rückstoßkräften
Bei der Explosionsdruckentlastung kommt es durch den Abströmprozeß von ,unverbranntem Gemisch und von Verbrennungsprodukten aus der Entlastungsöffnung zu einem Rückstoß. Die dabei auf die zu schützenden Anlagenteile ausgeübte Kraft hängt vom reduzierten Explosionsüberdruck und von der Entlastungsfläche ab. Die maximale Rückstoßkraft FR,max läßt sich aus dem maximalen reduzierten Explosionsüberdruck pred,max und der Entlastungsfläche A nach der Gleichung
| FR, max = α × A × pred,max | in kN | (16) |
berechnen [18 bis 22]. α ist der sogenannte Dynamikkoeffizient. Für alle Fälle der Praxis ist es ausreichend, wenn α =119 gesetzt wird.
Für die praktische Auslegung der einen explosionsdruckentlasteten Behälter stützenden Baukonstruktion ist jedoch nicht nur die berechnete maximale Rückstoßkraft allein, sondern auch deren zeitlicher Ablauf maßgebend [19].
Die Dauer des Rückstoßes kann mit folgender Gleichung abgeschätzt werden [22]
| KSt × V | |||
| tD = 10-4 × |
| in s | (17) |
| A × pred,max |
Zur Berechnung des auf die druckentlastete Apparatur übertragenen Gesamtimpulses I kann der zeitliche Ablauf des Impulses auf einen flächengleichen Rechteckimpuls zurückgeführt werden. Als Maß für die Höhe des Rechteckimpulses kann für die Praxis 0,52 × FR,max gesetzt werden. Damit errechnet sich der übertragene Gesamtimpuls zu
I = 0.52 × FR,max × tD in kN × s (18)
Die Auswirkungen der Rückstoßkräfte auf die Struktur des explosionsdruckentlastenden Systems bedürfen darüber hinaus weiterer detaillierter Betrachtungen.
Durch gegenüberliegende Anordnung von gleich großen Entlastungsöffnungen kann die Wirkung der Rückstoßkräfte auf den entlasteten Behälter kompensiert werden.
9 Explosionsdruckentlastung von Behältern, die durch Rohre verbunden sind
Die Basisgleichungen und Nomogramme in den Bildern 9 und 10 ergeben zu kleine Entlastungsflächen, wenn eine Staubexplosion aus einem Behälter über eine Rohrleitung in einen anderen Behälter übertragen wird. Gesteigerte Turbulenz, Vorkompression und großflächige Flammenstrahlzündung können bei Leitungslängen > 6 m zu einer erhöhten Explosionsheftigkeit, d. h. zu einem überhöhten maximalen reduzierten Explosionsüberdruck führen. Explosionstechnische Entkopplungsmaßnahmen [1; 2] in der Verbindungsleitung sind daher notwendig.
Die Schutzmaßnahme Explosionsdruckentlastung kann nach dem gegenwärtigen Erkenntnisstand bei Verbindungsleitungslängen < 6 m bis zu Rohrnennweiten DN 300 ohne Entkopplungsmaßnahmen wie folgt angewendet werden:
- Die Entlastungseinrichtung ist für einen niedrigen statischen Ansprechüberdruck auszulegen (pstat < 0,2 bar).
- Bei gleich großen Behältern (ΔV ± 10%) sind beide Behälter gemäß Basisgleichungen (Nomogramme) zu entlasten.
- Bei unterschiedlich großen Behältern sind die Entlastungsflächen auf einen maximalen reduzierten Explosionsüberdruck von pred,max < 1,0 bar zu beziehen.
Die Behälterfestigkeit sollte einen Überdruck von 2 bar nicht unterschreiten.
Besteht keine Möglichkeit, den kleineren Behälter zu entlasten, so ist dieser explosionsfest für den maximalen Explosionsüberdruck auszulegen, und die Entlastungsflächen des größeren Behälters sind zu verdoppeln.
Besteht keine Möglichkeit den größeren Behälter zu entlasten, ist die Anwendung der Schutzmaßnahme Explosionsdruckentlastung nicht möglich. Für Rohrnennweiten DN > 300 ist die Stellungnahme von Fachleuten einzuholen.
10 Einfluß von Abblasrohren auf die Explosionsdruckentlastung
Ist einer Druckentlastungseinrichtung ein Abblasrohr nachgesetzt, so kann dieses nach dem Ansprechen der Entlastung bereits mit explosionsfähigem Gemisch gefüllt sein, bevor die Flammen aus dem zu schützenden Behälter austreten. Die Folge ist eine Sekundärexplosion im Abblasrohr, die den Entlastungsvorgang behindert. Hierbei wird der maximale reduzierte Explosionsüberdruck im Behälter angehoben. Die Druckwirkung hängt ab vom zu erwartenden maximalen reduzierten Explosionsüberdruck bei Vorhandensein einer Berstscheibe ohne Abblasrohr und von der Staubverteilung.
10.1 Berstscheiben als Druckentlastungseinrichtungen
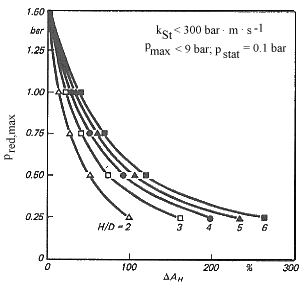
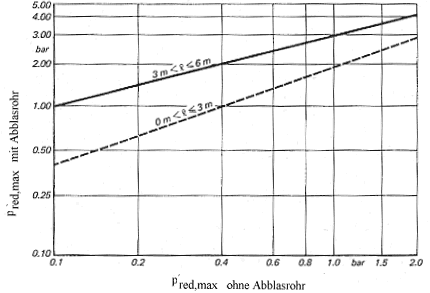
Bei homogenen Staub/Luft-Gemischen in explosionsdruckentlasteten kubischen Behältern mit Berstscheiben als Druckentlastungseinrichtungen kann der Einfluß von nachgesetzten Abblasrohren auf die Verstärkung der Explosionsheftigkeit in der zu schützenden Apparatur Bild 15 entnommen werden [24].
Die Darstellung sagt aus, daß die Zunahme des maximalen reduzierten Explosionsüberdruckes im zu schützenden Behälter gegenüber der freien Entlastung um so geringer ist, je kürzer das Abblasrohr ist. Mit Höchstwerten muß gerechnet werden, wenn die Geschwindigkeit der Sekundärexplosion Schallgeschwindigkeit erreicht. Dies kann in Abblasrohren eintreten, deren Länge 3 m übersteigt.
Entsprechend der zu erwartenden Zunahme des maximalen reduzierten Explosionsüberdruckes pred,max ist die Explosionsfestigkeit p des zu schützenden Behälters wie folgt zu erhöhen (Bild 15):
Abblasrohrlänge 0 m < l < 3 m
| p = p´red, max = 1.84 p | 0.654 | in bar (19) |
| red,max |
Abblasrohrlänge 3 m < l < 6 m
| p = p´red, max = 3.00 p | 0.4776 | in bar (20) |
| red,max |
Bild 15. Einfluß von Abblasrohren auf die Erhöhung des maximalen reduzierten Explosionsüberdruckes pred,max im zu schützenden kubischen Behälter mit Berstscheiben
homogene Staubverteilung l = Abblasrohrlänge
Ist hingegen die Behälterfestigkeit p = pred,max vorgegeben, dann ist die Entlastungsfläche A so zu vergrößern, daß sich folgender maximaler reduzierter Explosionsüberdruck pred, max bei freier (ungehinderter) Entlastung einstellt:
Abblasrohrlänge 0 m < l < 3 m:
| p = p´red,max = 0.3936 p´ | 1.529 | in bar (21) |
| red,max |
Abblasröhrlänge 3 m < l < 6 m
| p = pred,max = 0.1002 p´ | 2.0938 | in bar (22) |
| red,max |
Werden also bei freier Entlastung - gemäß Nomogrammdarstellung - Werte für pred,max von 0,2 bar bis 0,8 bar zugrunde gelegt, so muß bei Anwendung von längeren (l >3 m) Abblasrohren die Explosionsfestigkeit des zu schützenden Behälters mindestens 1,4 bar bis 2,7 bar betragen. Behälter, deren Explosionsfestigkeit unterhalb von 1 bar Überdruck liegt, können in Verbindung mit längeren Abblasrohren durch Explosionsdruckentlastung (zu große Entlastungsflächen) nicht mehr abgesichert werden.
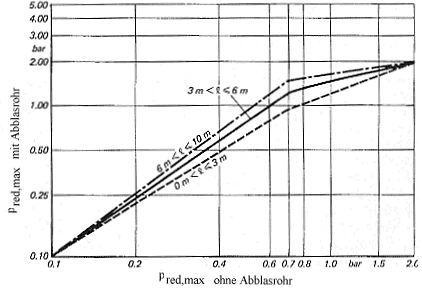
Beim pneumatischen Befüllen von kubischen Behältern mit brennbaren Stäuben entstehen inhomogene Staub/Luft-Gemische [10; 11]. Hierdurch wird das Austreten von unverbranntem Staub und auch das Entstehen von Staub/Luft-Gemischen im nachgesetzten Abblasrohr nach dem Ansprechen der Berstscheibe eingeschränkt. Gegenüber homogenen Staub/Luft-Gemischen (Bild 15) ist der Einfluß auf den maximalen reduzierten Explosionsüberdruck im zu schützenden Behälter deutlich geringer (Bild 16). Zahlenwertgleichungen für die Berechnung der Zunahme des maximalen reduzierten Explosionsüberdruckes pred,max bzw. für die Flächenvergrößerung bei vorgegebener Behälterfestigkeit p sind [25; 26] zu entnehmen.
Bild 16. Einfluß von Abblasrohren auf die Erhöhung des maximalen reduzierten Explosionsüberdruckes pred,max im zu schützenden kubischen Behälter mit Berstscheiben
inhomogene Staubverteilung beim pneumatischen Befüllen
l = Abblasrohrlänge
Dieser Einfluß braucht daher bei inhomogenen Staub/Luft-Gemischen nicht berücksichtigt zu werden, wenn die Behälterfestigkeit p > 2 bar ist oder wenn bei einer Behälterfestigkeit von p > 0,25 bar die Entlastungsfläche so groß gewählt wird, daß der maximale reduzierte Explosionsüberdruck dem Ansprechüberdruck (pred,max = pstat = 0,1 bar) der Berstscheibe entspricht.
10.2 Explosionsklappen als Druckentlastungseinrichtungen
Es kann davon ausgegangen werden, daß der Einfluß von Abblasrohren nach Explosionsklappen mit einer sehr guten Entlastungsfähigkeit auf die Anhebung der Druckwirkung im zu schützenden Behälter ähnlich ist wie bei der Anwendung von Berstscheiben mit vergleichbarer Entlastungsfähigkeit (siehe Abschnitt 10.1).
Untersuchungen mit homogenen Staub/Luft-Gemischen und rechteckigen Explosionsklappen geringerer Entlastungsfähigkeit haben ergeben, daß in bestimmten Fällen bei Explosionsklappen mit hohem Deckelgewicht der Einfluß von Abblasrohren geringer ist [8]. Ursache hierfür ist, daß nach dem Ansprechen der Explosionsklappe der Ausschub von unverbranntem Staub/Luft-Gemisch in das Abblasrohr begrenzt wird. Hierdurch wird die Staubkonzentration gering gehalten, und die volle Ausbildung einer Sekundärexplosion wird verhindert, wenn Staubablagerungen im Bereich der Einbaustelle vermieden werden können. In diesem Fall kann die Explosionsfestigkeit der zu schützenden Behälter geringer sein als bei Berstscheiben und Explosionsklappen hoher Entlastungsfähigkeit.
10.3 Konstruktive Gestaltung von Abblasrohren
Abblasrohre (Abblaskanäle) sollten möglichst kurz sein und gerade verlegt werden [1; 24]. Der Winkel zur Achse der Entlastungsöffnung darf 20° nicht überschreiten. Abblasrohre müssen mindestens den Querschnitt der Entlastungsöffnung und die Explosionsfestigkeit des zu schützenden Behälters haben. Bei Rohrlängen von mehr als 3 m wird empfohlen, diese mit Nenndruck PN 6 oder PN 10 auszuführen. Runde Abblasrohre sind aus Festigkeitsgründen vorzuziehen.
Wenn aus Wartungsgründen in der Nähe der Entlastungseinrichtung eine Inspektionsöffnung vorgesehen wird, so müssen Deckel und Verschluß die gleiche Festigkeit wie das Abblasrohr haben. Grundsätzlich dürfen Abblasrohre nicht verschlossen werden. Jedoch sind leichte Abdeckungen, z.B. Folien oder Scheiben in Klemmprofilen, zulässig, um z.B. das Eindringen von Regen und Schnee zu verhindern. Diese Abdeckungen müssen bei sehr niedrigen Ansprechüberdrücken (pstat < 0,1 bar) den Abblasrohrquerschnitt freigeben.
 | weiter . |  |
...
X
⍂
↑
↓
