umwelt-online: Archivdatei - DIN 1045-1 - Tragwerke aus Beton, Stahlbeton und Spannbeton

umwelt-online: DIN 1045-1 Tragwerke aus Beton, Stahlbeton und Spannbeton; Bemessung und Konstruktion (8)

10.4.3 Wölbkrafttorsion

(1) Spannungen aus behinderter Querschnittsverwölbung dürfen im Allgemeinen im Grenzzustand der Tragfähigkeit vernachlässigt werden.

(2) Bei geschlossenen dünnwandigen Querschnitten und bei Vollquerschnitten dürfen Wölbspannungen im Allgemeinen generell vernachlässigt werden.

10.4.4 Unbewehrte Bauteile

(1) Für Torsion und kombinierte Beanspruchung aus Torsion und Querkraft gilt 10.3.7 analog.

(2) Bei einem gerissenen Bauteil darf nicht ohne weiteres vorausgesetzt werden, dass es Torsionsmomente aufnimmt, sofern nicht eine ausreichende Tragfähigkeit hierfür nachgewiesen werden kann.

10.5 Durchstanzen

10.5.1 Allgemeines

(1) Die Grundsätze und Regeln dieses Abschnitts ergänzen die Regeln in 10.3. Sie betreffen das Durchstanzen von Platten mit Biegebewehrung nach 10.2; sie gelten auch für das Durchstanzen von Fundamenten und von Rippendecken mit einem Vollquerschnitt im Bereich der Lasteinleitungsfläche, sofern der Vollquerschnitt mindestens um das Maß 1,5d über den kritischen Rundschnitt hinausreicht.

(2) Durchstanzen kann aus konzentrierten Lasten oder Auflagerreaktionen herrühren, die auf einer relativ kleinen Fläche wirken. Letztere wird als Lasteinleitungsfläche A_load bezeichnet.

(3) Ein geeignetes Bemessungsmodell für den Nachweis gegen Durchstanzen im Grenzzustand der Tragfähigkeit ist in Bild 37 angegeben. Die kritische Fläche A_crit ist dabei parallel zur Lasteinleitungsfläche A_load anzunehmen.

(4) Der Nachweis der Tragfähigkeit ist längs festgelegter Nachweisschnitte zu führen. Außerhalb des Bereichs der Nachweisschnitte muss das Bauteil die Anforderungen nach 10.3 erfüllen.

Bild 37 - Bemessungsmodell für den Nachweis der Sicherheit gegen Durchstanzen

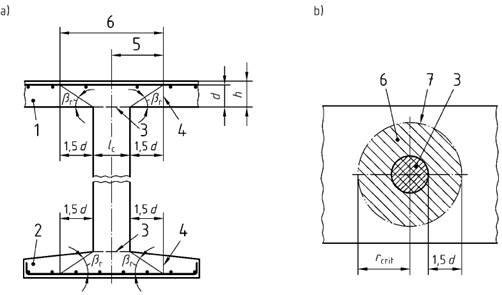
Legende

a)	Querschnitt
b)	Plattendraufsicht
	β_r = 33,7°

1	Platte	4	kritischer Rundschnitt	7	Umfang des kritischen Rundschnitts u_crit
2	Fundamentplatte	5	kritischer Radius
3	Lasteinleitungsfläche A_load	6	kritische Fläche A_crit

10.5.2 Lasteinleitung und Nachweisschnitte

(1) Die Festlegungen dieses Abschnitts sind auf die folgenden Arten von Lasteinleitungsflächen A_load anwendbar:

kreisförmige Flächen mit einem Durchmesser bis 3,5d (d ist dabei die mittlere statische Nutzhöhe des nachzuweisenden Bauteils),
rechteckige Flächen mit einem Umfang nicht größer als 11d und einem Verhältnis von Länge a zu Breite b der Fläche von maximal 2,0,
Flächen mit beliebiger Form, die sinngemäß wie die oben erwähnten Formen begrenzt sind.

Die Rundschnitte benachbarter Lasteinleitungsflächen nach den Absätzen (3) und (5) dürfen sich dabei nicht überschneiden.

(2) Wenn die Bedingungen nach Absatz (1) bei Auflagerung auf Wänden oder Stützen nicht erfüllt werden, weil sich in diesem Fall die Querkräfte auf die Ecken der Auflagerflächen konzentrieren, sind Rundschnitte nach Bild 38 anzusetzen, sofern kein genauerer Nachweis geführt wird.

Bild 38 - Maßgebende Abschnitte für den kritischen Rundschnitt bei ausgedehnten Auflagerflächen

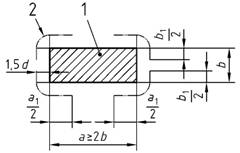
Legende

1	Lasteinleitungsfläche A_load
2	maßgebende Abschnitte des kritischen Rundschnitts

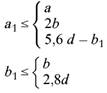(3) Der kritische Rundschnitt für runde oder rechteckige Lasteinleitungsflächen, die sich nicht in der Nähe von freien Rändern befinden, umgibt die Lasteinleitungsfläche in einem Abstand von 1,5d (siehe Bild 39).

Bild 39 - Kritischer Rundschnitt um Lasteinleitungsflächen, die sich nicht in der Nähe eines freien Randes befinden

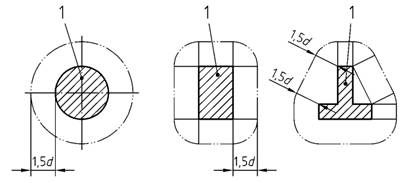
Legende

1	Lasteinleitungsfläche A_load

(4) Die kritische Fläche A_crit ist die Fläche innerhalb des kritischen Rundschnitts.

(5) Weitere Rundschnitte innerhalb und außerhalb der kritischen Fläche sind affin zum kritischen Rundschnitt anzunehmen.

(6) Für Lasteinleitungsflächen, deren Rand nicht mehr als 6d von Öffnungen entfernt ist, ist ein der Öffnung zugewandter Teil des maßgebenden Rundschnitts als unwirksam zu betrachten. Dieser Umfangsabschnitt wird durch den Abstand der Schnittpunkte der Verbindungslinien mit dem betrachteten Rundschnitt nach Bild 40 beschrieben.

Bild 40 - Kritischer Rundschnitt in der Nähe von Öffnungen

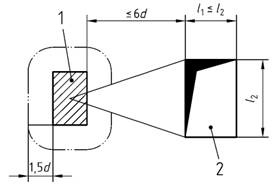
Legende

1	Lasteinleitungsfläche A_load
2	Öffnung
	Wenn l₁ > l₂, dann gilt l₂ = (l₁ * l₂)^0,5

(7) Bei Lasteinleitungsflächen, die sich in der Nähe eines freien Randes oder einer freien Ecke befinden, ist der kritische Rundschnitt nach Bild 41 anzunehmen, sofern dieser einen Umfang ergibt (freier Rand ausgeschlossen), der kleiner als derjenige nach den Absätzen (3) und (6) ist.

(8) Bei Lasteinleitungsflächen im Bereich eines freien Randes mit einem Randabstand von mehr als 3d zum freien Plattenrand, darf die aufnehmbare Querkraft mit einem kritischen Rundschnitt nach Bild 39 bestimmt werden.

Bild 41 - Kritischer Rundschnitt nahe freien Rändern

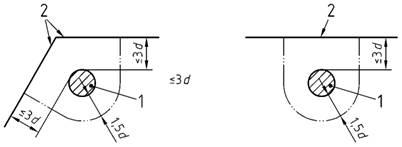
Legende

1	Lasteinleitungsfläche A_load
2	freier Rand

(9) Bei Lasteinleitungsflächen, die sich nahe oder an einem freien Rand oder einer Ecke befinden, d. h. mit einem Randabstand kleiner als d, ist stets eine besondere Randbewehrung nach 13.3.2 (10) mit einem Abstand der Steckbügel s_w < 100 mm längs des freien Randes erforderlich.

(10) Bei Stützen mit schräger Stützenkopfverstärkung mit l_H < 1,5 h_H (siehe Bild 42) ist nur im kritischen Rundschnitt außerhalb der Stützenkopfverstärkung ein Nachweis erforderlich. Der Abstand r_crit dieses Schnittes vom Schwerpunkt der Lasteinleitungsfläche darf nach Gleichung (96) ermittelt werden:

r_crit = 1,5d + l_H + 0,5 l_c

(96)

Dabei ist

l_H	der Abstand des Stützenrands vom Rand der Stützenkopfverstärkung
l_c	der Durchmesser einer Lasteinzugsfläche mit Kreisquerschnitt

Bei Rechteckstützen mit einer rechteckigen Stützenkopfverstärkung mit l_H < 1,5d (siehe Bild 42) und den Gesamtabmessungen b_c und h_c im Grundriss (mit b_c < h_c) ist r_crit als der jeweils kleinere der folgenden Werte anzunehmen:

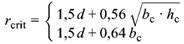(97)

Bei Stützen mit abgestufter Stützenkopfverstärkung mit l_H < 1,5h_H ist die gesamte Fläche der Stützenkopfverstärkung als Lasteinleitungsfläche anzunehmen.

Bild 42 - Platte mit einer Stützenkopfverstärkung mit l_H < 1,5 h_H

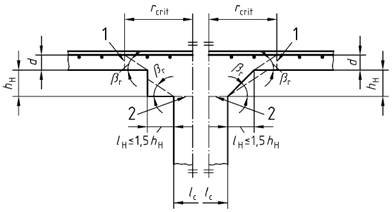
Legende

1	kritischer Rundschnitt
2	Lasteinleitungsfläche A_load

(11) Bei Platten mit einer Stützenkopfverstärkung mit l_H > 1,5h_H (siehe Bild 43) sind neben dem kritischen Rundschnitt außerhalb der Stützenkopfverstärkung auch kritische Rundschnitte im Bereich der Stützenkopfverstärkung nachzuweisen.

(12) Die Abstände vom Mittelpunkt der Lasteinleitungsfläche zu den kritischen Rundschnitten nach Bild 43 dürfen wie folgt angenommen werden:

r_{crit, ex} = 1,5d + l_H + 0,5 l_c	(98)
r_{crit, in} = 1,5 (d + d_H) + 0,5 l_c	(99)

(13) Die Festlegungen in 10.5.3 sind auch für Nachweise innerhalb der Stützenkopfverstärkung anwendbar, wobei d mit d_H nach Bild 43 anzunehmen ist.

Bild 43 - Platte mit Stützenkopfverstärkung mit l_H > 1,5 h_H

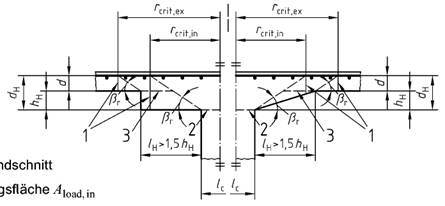
Legende

1	kritischer Rundschnitt
2	Lasteinleitungsfläche A_{load, in}
3	Lasteinleitungsfläche A_{load, ex}

10.5.3 Nachweisverfahren

(1) Das Bemessungsverfahren für Durchstanzen basiert auf einem räumlichen Fachwerkmodell. Dieses

Fachwerkmodell wird durch die folgenden Bemessungswerte der Querkrafttragfähigkeitje Längeneinheit beschrieben, wobei die Nachweisschnitte nach Bild 45 affin zum kritischen Rundschnitt verlaufen:

v_{Rd, ct}	Bemessungswert der Querkrafttragfähigkeit längs des kritischen Rundschnitts einer Platte ohne Durchstanzbewehrung.
v_{Rd, ct, a}	Bemessungswert der Querkrafttragfähigkeit längs des äußeren Rundschnitts außerhalb des durchstanzbewehrten Bereichs. Dieser Bemessungswert beschreibt den Übergang vom Durchstanzwiderstand ohne Querkraftbewehrung v_{Rd, ct} zum Querkraftwiderstand nach 10.3.3 in Abhängigkeit von der Breite l_w des durchstanzbewehrten Bereiches (siehe Bild 45).
v_{Rd, sy}	Bemessungswert der Querkrafttragfähigkeit mit Durchstanzbewehrung längs innerer Nachweisschnitte.
v_{Rd, max}	Bemessungswert der maximalen Querkrafttragfähigkeit längs des kritischen Rundschnitts.

(2) Die aufzunehmende Querkraft im betrachteten Nachweisschnitt je Längeneinheit beträgt:

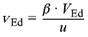(100)

Dabei ist

V_Ed	der Bemessungswert der gesamten aufzunehmenden Querkraft
u	der Umfang des betrachteten Rundschnitts nach Bild 45
β	der Beiwert zur Berücksichtigung der nichtrotationssymmetrischen Querkraftverteilung im Rundschnitt bei Rand- und Eckstützen sowie bei Innenstützen in unregelmäßigen Systemen. Für unverschiebliche Systeme dürfen die Werte nach Bild 44 angenommen werden, sofern kein genauerer Nachweis geführt wird. Für verschiebliche Systeme sind im Allgemeinen genauere Untersuchungen erforderlich

(3) Ein Reduzieren der einwirkenden Querkraft aus auflagernahen Einzellasten nach 10.3.2 ist nicht zulässig.

(4) Bei Fundamentplatten darf die Querkraft V_Ed um die günstige Wirkung der Bodenpressung in der kritischen Fläche abgemindert werden. Dabei dürfen für die Ermittlung der resultierenden Bodenreaktionskraft jedoch höchstens 50 % der kritischen Fläche A_crit nach 10.5.2 (4) in Ansatz gebracht werden.

(5) Die Querkraftkomponente V_pd der Spanngliedkraft von geneigten Spanngliedern, die parallel zu V_Ed wirkt und innerhalb der betrachteten Rundschnitte liegt, darf nach 10.3.2 berücksichtigt werden.

(6) Bei Platten ohne Durchstanzbewehrung ist nachzuweisen, dass längs des kritischen Rundschnitts nach 10.5.2 gilt:

v_Ed < v_{Rd, ct}

(101)

(7) Bei Platten mit Durchstanzbewehrung sind folgende Nachweise zu führen:

Die aufzunehmende Querkraft v_Ed nach Gleichung (100) längs des kritischen Rundschnitts darf den Bemessungswert der maximalen Querkrafttragfähigkeit nicht überschreiten:

v_Ed < v_{Rd, max} (102)
In jedem inneren Rundschnitt nach Bild 45 ist nachzuweisen:

v_Ed < v_{Rd, sy} (103)
Zur Vermeidung eines Versagens außerhalb des durchstanzbewehrten Bereiches ist längs des äußeren Rundschnitts nachzuweisen:

v_Ed < v_{Rd, ct, a} (104)

Bild 44 - Näherungswerte für den Beiwert β

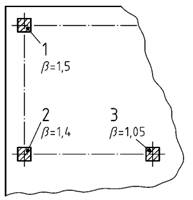
Legende

1	Eckstütze
2	Randstütze
3	Innenstütze

10.5.4 Platten oder Fundamente ohne Durchstanzbewehrung

Die Querkrafttragfähigkeit v_{Rd, ct} längs des kritischen Rundschnitts nach 10.5.2 ist nach Gleichung (105) zu ermitteln:

v_{Rd, ct} = [0,14η₁ κ * (100 * ρ_l * f_ck)^1/3 - 0,12σ_cd] * d

(105)

mit

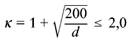(106)

Dabei ist

η₁	= 1,0 für Normalbeton; für Leichtbeton nach Tabelle 10
d	die mittlere Nutzhöhe in mm
	d = (d_x + d_y) /2
d_x + d_y	die Nutzhöhe der Platte in x- bzw. y-Richtung im betrachteten Rundschnitt
ρ_l	der mittlere Längsbewehrungsgrad innerhalb des betrachteten Rundschnitts mit

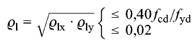ρ_lx, ρ_ly	der Bewehrungsgrad, bezogen jeweils auf die Zugbewehrung in x- bzw. y-Richtung, die innerhalb des betrachteten Rundschnitts im Verbund liegt und außerhalb des betrachteten Rundschnittes verankert ist. Bei Eck- und Randstützen siehe 10.5.2 (9).
σ_cd	der Bemessungswert der Betonnormalspannung innerhalb des betrachteten Rundschnitts mit


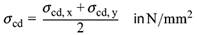σ_{cd, x}, σ_{cd, y}	die Bemessungswerte der Betonnormalspannung innerhalb des betrachteten Rundschnitts in x- bzw. y-Richtung
N_{Ed, x}, N_{Ed, y}	die Bemessungswerte der mittleren Längskräfte in den Querschnitten A_{c, x} und A_{c, y} durch den kritischen Rundschnitt infolge Vorspannung oder sonstige Einwirkungen (N_Ed < 0 als Längsdruckkraft)

10.5.5 Platten oder Fundamente mit Durchstanzbewehrung

(1) Die maximale Querkrafttragfähigkeit v_{Rd, max} für Platten mit Durchstanzbewehrung im kritischen Rundschnitt ist mit Gleichung (107) zu ermitteln:

v_{Rd, max} = 1,5 v_{Rd, ct}

(107)

(2) Bei Durchstanzbewehrung rechtwinklig zur Plattenebene ist die erforderliche Bewehrung für die jeweils betrachtete Bewehrungsreihe nach Bild 45 aus Gleichung (108) und Gleichung (109) zu ermitteln und auf dem betrachteten Umfang gleichmäßig verteilt anzuordnen (siehe 13.3.3):

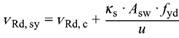für die erste Bewehrungsreihe im Abstand 0,5 d vom Stützenrand gilt:

(108)
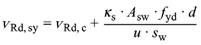für die weiteren Bewehrunqsreihen im Abstand s_w < 0,75d untereinander gilt:

(109)

Dabei ist

v_{Rd, c}	der Betontraganteil; es darf v_{Rd, c} = v_{Rd, ct} nach Gleichung (105) angenommen werden
κ_s * A_sw * f_yd	die Bemessungskraft der Durchstanzbewehrung in Richtung der aufzunehmenden Querkraft für jede Reihe der Bewehrung
u	der Umfang des Nachweisschnittes
s_w	die wirksame Breite einer Bewehrungsreihe nach Bild 45, mit: s_w < 0,75d
κ_s	der Beiwert zur Berücksichtigung des Einflusses der Bauteilhöhe auf die Wirksamkeit der Bewehrung mit
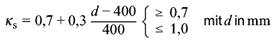		(110)

(3) Werden Schrägstäbe als Durchstanzbewehrung eingesetzt, müssen diese eine Neigung von 45° < α < 60° gegen die Plattenebene aufweisen. Werden ausschließlich Schrägstäbe eingesetzt, so dürfen diese nur im Bereich von 1,5d (mit der statischen Nutzhöhe d der Platte oder des Fundaments) um die Stütze angeordnet werden (siehe Bild 72).

Die erforderliche Bewehrung ist in einem Schnitt im Abstand 0,5 d vom Stützenrand nach Gleichung (111) nachzuweisen.

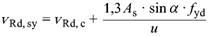(111)

Dabei ist

1,3A_s * sinα * f_yd	die Bemessungskraft der Durchstanzbewehrung in Richtung der aufzunehmenden Querkraft
α	der Winkel der geneigten Durchstanzbewehrung gegen die Plattenebene (siehe Bild 45)

(4) Der äußere Rundschnitt liegt im Abstand 1,5 d von der letzten Bewehrungsreihe (siehe Bild 45). Die Querkrafttragfähigkeit längs des äußeren Rundschnitts ist wie folgt zu ermitteln:

v_{Rd, ct, a} = κ_a * v_{Rd, ct}

(112)

Dabei ist

v_{Rd, ct}	die Tragfähigkeit ohne Durchstanzbewehrung nach Gleichung (105) unter Berücksichtigung des Längsbewehrungsgrades ρ_l im äußeren Rundschnitt
κ_a	der Beiwert zur Berücksichtigung des Übergangs zum Plattenbereich mit der Tragfähigkeit nach 10.3.3 mit
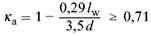		(113)
l_w	die Breite des Bereiches mit Durchstanzbewehrung außerhalb der Lasteinleitungsfläche (siehe Bild 45)

Bild 45 - Nachweisschnitte der Durchstanzbewehrung

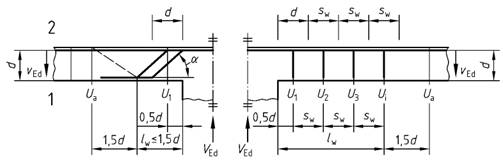
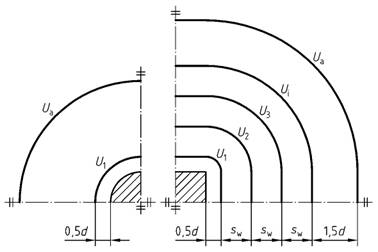
Legende

1	Nachweisschnitt
2	wirksame Breite einer Bügelreihe s_w

(5) Anforderungen an die bauliche Durchbildung der Durchstanzbewehrung sind in 13.3.3 angegeben; die erforderliche Durchstanzbewehrung der inneren Rundschnitte darf folgenden Wert nicht unterschreiten:

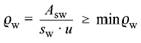(114)

bzw.

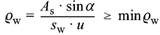bei geneigter Durchstanzbewehrung mit s_w = d und mit minρ_w nach 13.2.3 (5).

10.5.6 Mindestmomente

(1) Um die Querkrafttragfähigkeit sicherzustellen, sind die Platten im Bereich der Stützen für Mindestmomente m_Ed zu bemessen, sofern die Schnittgrößenermittlung nicht zu höheren Werten führt.

(2) Wenn andere Festlegungen fehlen, sollten folgende Mindestmomente je Längeneinheit angesetzt werden:

m_{Ed, x} = η_x * V_Ed

und

m_{Ed, y} = η_y * V_Ed

(115)

Dabei ist

V_Ed	die aufzunehmende Querkraft
η_x, η_y	der Momentenbeiwert nach Tabelle 14 für die x- bzw. . y-Richtung (siehe Bild 46)

Diese Mindestmomente sollten jeweils in einem Bereich mit der in Tabelle 14 angegebenen Breite angesetzt werden (siehe Bild 46).

Tabelle 14 - Momentenbeiwerte η und Verteilungsbreiten der Momente

Zeile	Spalte	1	2	3	4	5	6
	Spalte	η_x		anzusetzende Breite ^b	η_y
	Lage der Stütze	Zug an der Plattenoberseite	Zug an der Plattenunterseite	anzusetzende Breite ^b	Zug an der Plattenoberseite ^c	Zug an der Plattenunterseite	anzusetzende Breite
1	Innenstütze	0,125	0	0,3 l_y	0,125	0	0,3 l_x
2	Randstütze, Rand "x" ^a	0,25	0	0,15 l_y	0,125	0,125	(je m Plattenbreite)
3	Randstütze "y" ^a	0,125	0,125	(je m Plattenbreite)	0,25	0	0,15 l_x
4	Eckstütze	0,5	0,5	(je m Plattenbreite)	0,5	0,5	(je m Plattenbreite)

a	Definition der Ränder und der Stützenabstände l_x und l_y siehe Bild 46
b	siehe Bild 46
c	Die Plattenoberseite bezeichnet die der Lasteinleitungsfläche entgegen liegende Seite der Platte; die Plattenunterseite diejenige Seite, auf der die Lasteinleitungsfläche liegt.

Bild 46 - Bereiche für den Ansatz der Mindestbiegemomente m_{Ed, x} und m_{Ed, y}

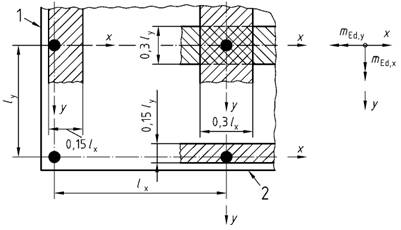
Legende

1	Rand "y"
2	Rand "x"

10.6 Stabwerkmodelle

10.6.1 Allgemeines

(1) Ein Stabwerkmodell besteht aus Betondruckstreben, aus Zugstreben und den verbindenden Knoten. Die Kräfte in diesen Elementen des Stabwerkmodells sind unter Einhaltung des Gleichgewichts für die Einwirkungen im Grenzzustand der Tragfähigkeit zu ermitteln, und die Elemente sind dafür nach den in 10.6.2 und 10.6.3 angegebenen Regeln zu bemessen.

(2) Die Zugstreben des Stabwerkmodells müssen nach Lage und Richtung mit der zugehörigen Bewehrung übereinstimmen.

(3) Um die Verträglichkeit näherungsweise sicherzustellen, sollte das Stabwerkmodell, insbesondere die Lage und Richtung wichtiger Druckstreben, an der Spannungsverteilung nach der linearen Elastizitätstheorie orientiert sein.

(4) Stabwerkmodelle dürfen kinematisch sein, wenn Geometrie und Belastung aufeinander abgestimmt sind.

(5) Bei der Stabkraftermittlung für statisch unbestimmte Stabwerkmodelle dürfen die unterschiedlichen Dehnsteifigkeiten der Druck- und Zugstreben näherungsweise berücksichtigt werden. Vereinfachend dürfen einzelne statisch unbestimmte Stabkräfte in Anlehnung an die Kräfte aus einer linear-elastischen Berechnung des Tragwerks gewählt werden.

(6) Die Ergebnisse aus mehreren Stabwerkmodellen dürfen im Allgemeinen nicht überlagert werden. Dies ist im Ausnahmefall möglich, wenn die Stabwerkmodelle für jede Einwirkung im Wesentlichen übereinstimmen.

10.6.2 Bemessung der Zug- und Druckstreben

(1) Die Druckstreben des Stabwerkmodells sind für Druck und für Querzug (siehe Bild 47), bei ebenen Stabwerkmodellen auch für Querzug senkrecht zur Ebene des Stabwerkmodells, zu bemessen. Die Querzugkraft im Druckfeld infolge einer Einschnürung an einem Knoten kann mit Hilfe eines örtlichen Stabwerkmodells ermittelt werden.

Bild 47 - Querzugkräfte in einem Druckfeld mit Einschnürung zu konzentrierten Knoten an beiden Enden

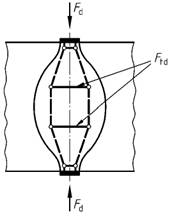
(2) Der Bemessungswert der Druckstrebenfestigkeit ist wie folgt begrenzt:

σ_{Rd, max} = 1,0η₁ * f_cd für ungerissene Betondruckzonen
σ_{Rd, max} = 0,75η₁ * f_cd für Druckstreben parallel zu Rissen

mit η₁ = 1,0 für Normalbeton; für Leichtbeton nach Tabelle 10

Bei Druckstreben mit kreuzenden Rissen können kleinere Werte erforderlich sein (siehe DAfSbHeft 525).

(3) Der Bemessungswert der Stahlspannung der Bewehrung der Zugstreben und der Bewehrung zur Aufnahme der Querzugkräfte in Druckstreben ist bei Betonstahl auf f_yd, bei Spannstahl auf f_p0,1k /γs zu begrenzen.

(4) Die Bewehrung ist bis in die konzentrierten Knoten ungeschwächt durchzuführen. Sie darf in verschmierten Knoten, die sich im Tragwerk über eine größere Länge erstrecken, innerhalb des Knotenbereichs gestaffelt enden. Dabei muss sie alle durch die Bewehrung umzulenkenden Druckwirkungen erfassen.

(5) Die Verankerungslänge der Bewehrung in Druck-Zug-Knoten beginnt am Knotenanfang, wo erste Druckspannungen aus den Druckstreben auf die verankerte Bewehrung treffen und von ihr umgelenkt werden (siehe Bild 49).

(6) In Bauteilbereichen mit parallelem Druck- und Zuggurt ist die Höhe des Druckspannungsfeldes oder die Höhe des Spannungsblocks im Hinblick auf die Verträglichkeit zu begrenzen. So sollten diese Abmessungen nicht größer gewählt werden, als sie sich bei Annahme einer linearen Dehnungsverteilung ergeben.

Bild 48 - Knotenbereich für den Nachweis von Druckknoten

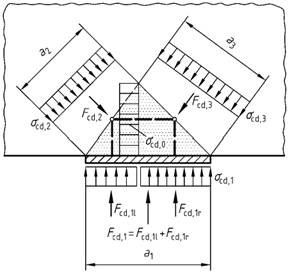
(7) Für Druckstreben, deren Druckfelder sich zu konzentrierten Knoten hin stark einschnüren, erübrigen sich Nachweise der Druckspannungen, wenn die angrenzenden Knoten nach 10.6.3 nachgewiesen werden.

weiter .