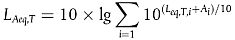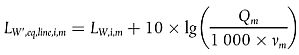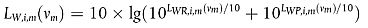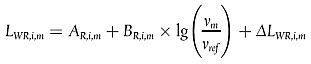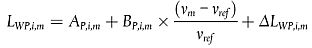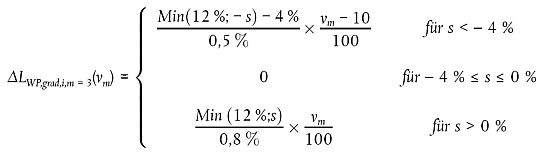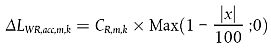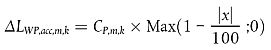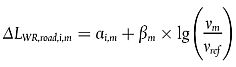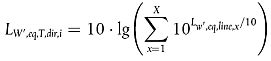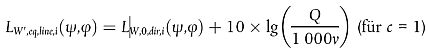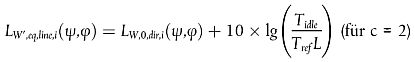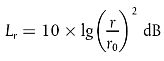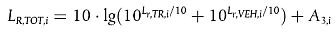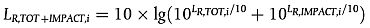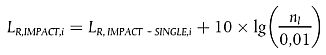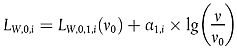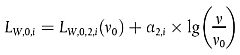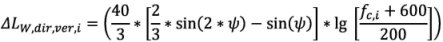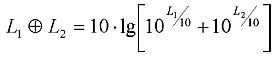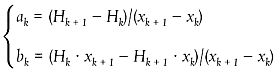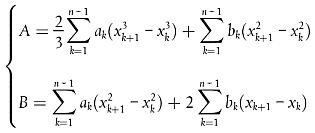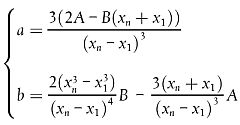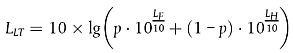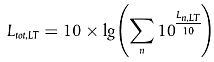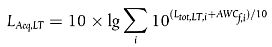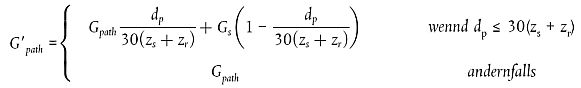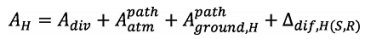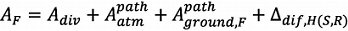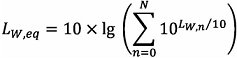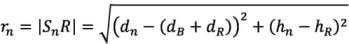Für einen individuellen Ausdruck passen Sie bitte die Für einen individuellen Ausdruck passen Sie bitte dieEinstellungen in der Druckvorschau Ihres Browsers an. ▢ Regelwerk, EU 2002, Lärm - EU Bund |  |
Richtlinie 2002/49/EG des Europäischen Parlaments und des Rates vom 25. Juni 2002 über die Bewertung und Bekämpfung von Umgebungslärm
(ABl. Nr. L 189 vom 18.07.2002 S. 12)
Stand: RL (EU) 2021/1226
| Bewertungsmethoden für Lärmindizes (nach Artikel 6 der Richtlinie 2002/49/EG) | Anhang II 15 21 |
1. Einleitung
Die Werte Lden und Lnight werden an den Messpunkten an den Immissionspunkten durch Berechnung anhand des in Kapitel 2 dargelegten Verfahrens und der in Kapitel 3 beschriebenen Daten bestimmt. Messungen können gemäß Kapitel 4 durchgeführt werden.
2. Gebräuchliche Verfahren zur Lärmbewertung
2.1. Allgemeine Bestimmungen - Straßenverkehrs-, Eisenbahn- und Industrie-/Gewerbelärm
2.1.1. Definition der Indizes, Frequenzbereiche und Frequenzbänder 21
Die Lärmberechnung ist im Frequenzbereich der Oktavbänder von 63 Hz bis 8 kHz vorzunehmen, und die Ergebnisse für die Frequenzbänder sind im entsprechenden Frequenzintervall vorzulegen.
Die Berechnung des Straßenverkehrs-, Eisenbahn- und Industrie-/Gewerbelärms erfolgt in Oktavbändern, ausgenommen jedoch die Schallleistung der Quelle des Schienenverkehrslärms, bei der die Terzbänder genutzt werden.
Für den Straßenverkehrs-, Eisenbahn- und Industrie-/Gewerbelärm, der auf diesen Oktavbandergebnissen beruht, wird der A-bewertete Langzeit-Dauerschallpegel für den Zeitraum Tag, Abend und Nacht gemäß Anhang I und Artikel 5 der Richtlinie 2002/49/EG durch die in den Abschnitten 2.1.2, 2.2, 2.3, 2.4 und 2.5 beschriebene Methode berechnet.
Für den Straßenverkehr und den Eisenbahnverkehr in Ballungsräumen wird der A-bewertete Langzeit-Dauerschallpegel durch den Beitrag der darin enthaltenen Straßen- und Eisenbahnsegmente, einschließlich Hauptverkehrsstraßen und Haupteisenbahnstrecken, bestimmt.
|
| (2.1.1) |
Hierbei gilt:
Ai bezeichnet die A-Bewertungskorrektur gemäß IEC 61672-1
i = Frequenzbandindex
und T ist der Zeitraum Tag, Abend oder Nacht.
Lärmparameter:
| Lp | Momentaner Schalldruckpegel | [dB] (re 2 · 10-5 Pa) |
| LAeq,LT | Gesamt-Langzeit-Dauerschallpegel LAeq ausgehend von allen Quellen und Spiegelquellen am Punkt R | [dB] (re 2 · 10-5 Pa) |
| LW | In-Situ-Schallleistungspegel einer Punktquelle (Bewegung oder Stand) | [dB] (re 10-12 W) |
| LW,i,dir | Gerichteter In-Situ-Schallleistungspegel für das i-te Frequenzband | [dB] (re 10-12 W) |
| LW2 | Durchschnittlicher In-Situ-Schallleistungspegel je Meter Linienquelle | [dB/m] (re 10-12 W) |
Weitere physikalische Parameter:
| p | Effektivwert des momentanen Schalldrucks | [Pa] |
| p0 | Referenzschalldruck = 2 · 10-5 Pa | [Pa] |
| W0 | Referenzschallleistung = 10-12 W | [Watt] |
2.1.2. Qualitätsrahmen
Genauigkeit der Eingangswerte
Alle Eingangswerte, die den Emissionspegel einer Quelle beeinflussen, sind mit mindestens der Genauigkeit zu bestimmen, die einer Unsicherheit von ± 2 dB (A) im Emissionspegel der Quelle entspricht (wobei alle anderen Parameter unverändert bleiben).
Nutzung von Standardwerten
Bei der Anwendung des Verfahrens müssen die Eingangswerte der tatsächlichen Nutzung entsprechen. Generell dürfen keine Standardeingangswerte oder -annahmen zugrunde gelegt werden. Standardeingangswerte und -annahmen werden akzeptiert, wenn die Erfassung realer Daten mit unverhältnismäßig hohen Kosten verbunden ist.
Qualität der für die Berechnungen verwendeten Software
Die Konformität der zur Durchführung der Berechnungen verwendeten Software mit den Verfahren gemäß diesem Anhang ist dadurch nachzuweisen, dass die Ergebnisse anhand von Testfällen bestätigt werden.
2.2. Straßenverkehrslärm
2.2.1. Beschreibung der Quellen 21
Klassifizierung der Fahrzeuge
Die Quelle von Straßenverkehrslärm wird durch Kombination der Schallemission jedes einzelnen Fahrzeugs, das Teil des Verkehrsflusses ist, bestimmt. Die Fahrzeuge werden ausgehend von den Merkmalen ihrer Schallemission in fünf Klassen eingeteilt:
Klasse 1: Leichte Kraftfahrzeuge,
Klasse 2: Mittelschwere Fahrzeuge,
Klasse 3: Schwere Fahrzeuge,
Klasse 4: Zweirädrige Kraftfahrzeuge,
Klasse 5: Offene Kategorie.
Bei den zweirädrigen Kraftfahrzeugen erfolgt eine weitere Unterteilung in zwei Teilklassen, nämlich Mopeds und leistungsstärkere Krafträder, da sie sehr unterschiedlich gefahren werden und ihre Geräuschemissionen in der Regel weit auseinander liegen.
Die ersten vier Klassen sind zwingend vorgeschrieben, die fünfte Klasse ist optional. Sie ist für neue Fahrzeuge vorgesehen, die möglicherweise in Zukunft entwickelt werden und deren Schallemission sich so weit unterscheidet, dass für sie eine zusätzliche Klasse festgelegt werden muss. Dies könnten beispielsweise Elektro- oder Hybridfahrzeuge sein, die künftig entwickelt werden und sich erheblich von den Fahrzeugen in den Klassen 1 bis 4 unterscheiden.
Genaue Angaben zu den verschiedenen Fahrzeugklassen finden sich in Tabelle [2.2.a].
Tabelle [2.2.a] Fahrzeugklassen
| Klasse | Bezeichnung | Beschreibung | Fahrzeugklasse in EG-Typgenehmigung für vollständige Fahrzeuge 1 | |
| 1 | Leichte Kraftfahrzeuge | PKW, Lieferwagen ≤ 3,5 t, Geländewagen (SUV) 2, Großraumlimousinen 3, einschließlich Anhänger und Wohnwagen | M1 und N1 | |
| 2 | Mittelschwere Fahrzeuge | Mittelschwere Fahrzeuge, Lieferwagen > 3,5 t, Busse, Wohnmobile usw. mit zwei Achsen und Doppelbereifung auf der Hinterachse | M2, M3 und N2, N3 | |
| 3 | Schwere Fahrzeuge | Schwere Nutzfahrzeuge, Reisebusse, Busse, mit drei oder mehr Achsen | M2 und N2 mit Anhänger, M3 und N3 | |
| 4 | Zweirädrige Kraftfahrzeuge | 4a | Zwei-, drei- und vierrädrige Mopeds | L1, L2, L6 |
| 4b | Motorräder mit und ohne Seitenwagen, drei- und vierrädrige Motorräder | L3, L4, L5, L7 | ||
| 5 | Offene Klasse | Entsprechend dem künftigen Bedarf | k. A. | |
| 1) Richtlinie 2007/46/EG des Europäischen Parlaments und des Rates vom 5. September 2007 (ABl. Nr. L 263 vom 09.10.2007 S. 1) zur Schaffung eines Rahmens für die Genehmigung von Kraftfahrzeugen und Kraftfahrzeuganhängern sowie von Systemen, Bauteilen und selbstständigen technischen Einheiten für diese Fahrzeuge.
2) SUV (Sports Utility Vehicles) Geländewagen. 3) MPV (Multi-Purpose Vehicles) Mehrzweckfahrzeuge. | ||||
Anzahl und Position Ersatzschallquellen
Bei diesem Modell wird jedes Fahrzeug (Klassen 1, 2, 3, 4 und 5) durch eine einzige Punktquelle dargestellt, die gleichförmig abstrahlt. Die erste Reflexion an der Straßenoberfläche wird implizit behandelt. Wie in Abbildung [2.2.a] dargestellt, befindet sich die Punktquelle 0,05 m über der Straßenoberfläche.
Abbildung [2.2.a] Position der äquivalenten Punktquelle bei leichten Fahrzeugen (Klasse 1), schweren Fahrzeugen (Klassen 2 und 3) und zweirädrigen Kraftfahrzeugen (Klasse 4)
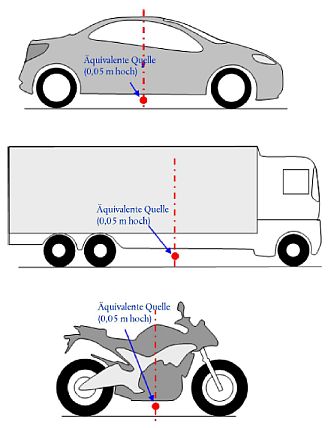
Die Darstellung des Verkehrsflusses erfolgt durch eine Linienquelle. Bei der Modellierung einer Straße mit mehreren Fahrspuren sollte idealerweise jede Fahrspur durch eine in ihrer Mitte verlaufende Linienquelle repräsentiert werden. Es ist jedoch auch akzeptabel, bei einer Straße mit zwei Richtungsfahrbahnen eine Linienquelle in der Straßenmitte oder bei mehrspurigen Straßen eine Linienquelle je Fahrbahn in der äußeren Fahrspur zu modellieren.
Schallleistungspegel
Allgemeine Betrachtungen
Da die Schallleistung der Quelle im "akustischen Halbraum" definiert wird, umfasst die Schallleistung auch den Effekt der Reflexion am Boden direkt unter der modellierten Quelle, wo es, abgesehen von der Reflexion an der Straßenoberfläche, die sich nicht direkt unter der modellierten Quelle befindet, keine störenden Gegenstände im unmittelbaren Umfeld gibt.
Verkehrsfluss
Die Schallemission eines Verkehrsflusses wird durch eine Linienquelle dargestellt, die durch ihre gerichtete Schallleistung je Meter pro Frequenz gekennzeichnet ist. Dies entspricht der Summe der Schallemission der einzelnen Fahrzeuge im Verkehrsfluss unter Berücksichtigung der von den Fahrzeugen im untersuchten Straßenabschnitt verbrachten Zeit. Die Darstellung des einzelnen Fahrzeugs im Fluss erfordert die Anwendung eines Verkehrsflussmodells.
Wird ein stetiger Verkehrsfluss von Qm Fahrzeugen der Klasse m je Stunde mit einer Durchschnittsgeschwindigkeit νm (in km/h) angenommen, so wird die gerichtete Schallleistung je Meter im Frequenzband i der Linienquelle LW', eq,line,i,m bestimmt durch:
|
| (2.2.1) |
wobei LW,i,m die gerichtete Schallleistung eines einzelnen Fahrzeugs ist. LW',m wird in dB angegeben (re 10-12 W/m). Diese Schallleistungspegel werden für jedes Oktavband i von 63 Hz bis 8 kHz berechnet.
Verkehrsflussdaten Qm sind als Jahresdurchschnitt je Stunde, je Zeitraum (Tag-Abend-Nacht), je Fahrzeugklasse und je Linienquelle anzugeben. Für alle Klassen sind die Eingabedaten für den Verkehrsfluss zu verwenden, die im Rahmen von Straßenverkehrszählungen oder mithilfe von Verkehrsmodellen ermittelt wurden.
Die Geschwindigkeit vm ist eine repräsentative Geschwindigkeit je Fahrzeugklasse: in den meisten Fällen die gesetzliche Höchstgeschwindigkeit für den Straßenabschnitt oder die gesetzliche Höchstgeschwindigkeit für die Fahrzeugklasse, je nachdem, welcher Wert niedriger ist.
Einzelnes Fahrzeug
Im Verkehrsfluss wird für alle Fahrzeuge der Klasse m angenommen, dass sie mit der gleichen Geschwindigkeit fahren, also vm.
Ein Straßenfahrzeug wird mittels einer Reihe mathematischer Gleichungen modelliert, die die beiden Hauptgeräuschquellen repräsentieren:
- Rollgeräusche aufgrund der Wechselwirkung Reifen/Straße;
- Antriebsgeräusche, die vom Antriebssystem (Motor, Auspuff usw.) des Fahrzeugs erzeugt werden.
Aerodynamische Geräusche sind in der Quelle für Rollgeräusche inbegriffen.
Für leichte, mittelschwere und schwere Kraftfahrzeuge (Klassen 1, 2 und 3) entspricht die Gesamtschallleistung der energetischen Summe der Roll- und der Antriebsgeräusche. Somit wird der Gesamtschallleistungspegel der Linienquellen m = 1, 2 oder 3 definiert durch:
|
| (2.2.2) |
wobei LWR,i,m der Schallleistungspegel für Rollgeräusche und LWP,i,m der Schallleistungspegel für Antriebsgeräusche ist. Dies gilt für alle Geschwindigkeitsbereiche. Bei Geschwindigkeiten unter 20 km/h entspricht der Schallleistungspegel dem Wert, wie er durch die Formel für vm = 20 km/h bestimmt ist.
Für zweirädrige Kraftfahrzeuge (Klasse 4) werden für die Quelle nur die Antriebsgeräusche berücksichtigt:
| LW,i,m = 4(νm = 4) = LWP,i,m = 4(νm = 4) | (2.2.3) |
Dies gilt für alle Geschwindigkeitsbereiche. Bei Geschwindigkeiten unter 20 km/h entspricht der Schallleistungspegel dem Wert, wie er durch die Formel für vm = 20 km/h bestimmt ist.
2.2.2. Referenzbedingungen
Die Quellengleichungen und -koeffizienten gelten für folgende Referenzbedingungen:
- konstante Fahrzeuggeschwindigkeit,
- ebene Straße,
- Lufttemperatur von τref = 20 °C,
- virtuelle Referenzstraßenoberfläche, bestehend aus einem einen durchschnittlichen Verdichtungsgrad aufweisenden Asphaltbeton 0/11 und Splittmastixasphalt 0/11, zwei bis sieben Jahre alt und in einem repräsentativen Instandhaltungszustand,
- eine trockene Straßenoberfläche,
- keine Spikereifen.
2.2.3. Rollgeräusche
Allgemeine Gleichung
Der Schallleistungspegel der Rollgeräusche im Frequenzband i für ein Fahrzeug der Klasse m = 1, 2 oder 3 wird definiert als:
|
| (2.2.4) |
Die Koeffizienten AR,i,m und BR,i,m sind für jede Fahrzeugklasse und für eine Referenzgeschwindigkeit von νref = 70 km/h in Oktavbändern gegeben. ΔLWR,i,m entspricht der Summe der Korrekturkoeffizienten, die auf die Rollgeräuschemissionen bei bestimmten Straßen- oder Fahrzeugbedingungen angewendet werden, die von den Referenzbedingungen abweichen:
| ΔLWR,i,m = ΔLWR,road,i,m + ΔLstuddedtyres,i,m + ΔLWR,acc,i,m + ΔLW,temp | (2.2.5) |
ΔLWR,road,i,m dient der Berücksichtigung des Einflusses, den eine Straßenoberfläche mit akustischen Eigenschaften, die von denen der virtuellen Referenzoberfläche nach Abschnitt 2.2.2 abweichen, auf die Rollgeräusche ausübt. Der Wert schließt den Einfluss sowohl auf die Ausbreitung als auch auf die Entstehung ein.
ΔLstudded tyres,i,m ist ein Korrekturkoeffizient für die höheren Rollgeräusche leichter Fahrzeuge mit Spikereifen.
ΔLWR,acc,i,m dient der Berücksichtigung des Einflusses, den eine Kreuzung mit Verkehrsampeln oder ein Kreisverkehr auf die Rollgeräusche ausübt. Der Wert schließt den Einfluss der Geschwindigkeitsveränderung auf die Geräuscherzeugung ein.
ΔLW,temp ist ein Term zur Korrektur einer Durchschnittstemperatur τ, die von der Referenztemperatur τref = 20 °C abweicht.
Korrektur um den Einfluss von Spikereifen
In den Fällen, in denen eine erhebliche Anzahl leichter Fahrzeuge im Verkehrsfluss jedes Jahr mehrere Monate lang Spikereifen benutzt, ist der dadurch bewirkte Einfluss auf die Rollgeräusche zu berücksichtigen. Für jedes Fahrzeug der Klasse m = 1, das mit Spikereifen ausgestattet ist, wird der geschwindigkeitsabhängige Anstieg der Rollgeräuschemissionen wie folgt bewertet:
|
| (2.2.6) |
wobei die Koeffizienten ai und bi für jedes Oktavband gegeben sind.
Die Zunahme der Rollgeräuschemissionen wird nur gemäß dem Anteil leichter Fahrzeuge mit Spikereifen und für einen begrenzten Zeitraum Ts (in Monaten) über das Jahr angerechnet. Wenn Qstud,ratio der durchschnittliche Anteil der mit Spikereifen ausgestatteten leichten Fahrzeuge am Gesamtaufkommen dieser Fahrzeuge je Stunde im Zeitraum Ts (in Monaten) ist, dann wird der jährliche durchschnittliche Anteil von mit Spikereifen ausgestatteten Fahrzeugen ps angegeben durch:
| ps = Qstud,ratio × (Ts/12) | (2.2.7) |
Die resultierende Korrektur der Schallleistung der Rollgeräuschemissionen aufgrund des Gebrauchs von Spikereifen für Fahrzeuge der Klasse m = 1 im Frequenzband i ist demnach:
|
| (2.2.8) |
Für die Fahrzeuge der anderen Klassen ist keine Korrektur vorzunehmen:
| ΔLstuddedtyres,i,m ≠ 1 = 0 | (2.2.9) |
Einfluss der Lufttemperatur auf die Rollgeräuschkorrektur
Die Lufttemperatur beeinflusst die Rollgeräuschemissionen in der Form, dass der Schallleistungspegel der Rollgeräusche mit steigender Lufttemperatur absinkt. Der Einfluss der Lufttemperatur wird in die Korrektur der Rollgeräusche auf der Straßenoberfläche einbezogen. Die Korrektur der Rollgeräusche auf der Straßenoberfläche wird normalerweise bei einer Lufttemperatur von τref = 20 °C bewertet. Im Falle einer anderen Jahresdurchschnittslufttemperatur (in °C) wird der durch die Straßenoberfläche verursachte Schall korrigiert durch:
| ΔLW,temp,m (τ) = Km × (τref - τ) | (2.2.10) |
Der Korrekturterm ist bei Temperaturen unter 20 °C positiv (d. h. der Schallpegel steigt) und bei höheren Temperaturen negativ (d. h. der Schallpegel sinkt). Der Koeffizient K ist abhängig von der Straßenoberfläche und den Reifenmerkmalen und weist im Allgemeinen eine gewisse Frequenzabhängigkeit auf. Bei allen Straßenoberflächen ist ein generischer Koeffizient für leichte Fahrzeuge (Klasse 1) von Km = 1 = 0,08 dB/°C und für schwere Fahrzeuge (Klassen 2 und 3) von Km = 2 = Km = 3 = 0,04 dB/°C anzuwenden. Der Korrekturkoeffizient ist auf alle Oktavbänder von 63 Hz bis 8.000 Hz gleichmäßig anzuwenden.
2.2.4. Antriebsgeräusche
Allgemeine Gleichung
Die Emission der Antriebsgeräusche umfasst die Gesamtheit der Anteile, die auf Motor, Auspuff, Getriebe, Lufteinlass usw. entfallen. Der Schallleistungspegel für die Antriebsgeräusche im Frequenzband i für ein Fahrzeug der Klasse m wird definiert als:
|
| (2.2.11) |
Die Koeffizienten AP,i,m und BP,i,m werden in Oktavbändern für jede Fahrzeugklasse und für eine Referenzgeschwindigkeit νref = 70 km/h angegeben.
ΔLWP,i,m entspricht der Summe der Korrekturkoeffizienten, die auf die Emission von Antriebsgeräuschen bei bestimmten Fahr- oder regionalen Bedingungen anzuwenden sind, die von den Referenzbedingungen abweichen:
| ΔLWP,i,m = ΔLWP,road,i,m + ΔLWP,grad,i,m + ΔLWP,acc,i,m | (2.2.12) |
ΔLWP,road,i,m dient der Berücksichtigung des Einflusses, den die Straßenoberfläche auf die Antriebsgeräusche mittels Absorption ausübt. Die Berechnung wird gemäß Abschnitt 2.2.6 durchgeführt.
ΔLWP,acc,i,m und ΔLWP,grad,i,m der Berücksichtigung des Einflusses, den Straßensteigungen und das Abbremsen und Beschleunigen,der Fahrzeuge an Straßenkreuzungen ausüben. Sie werden gemäß Abschnitt 2.2.4 bzw. 2.2.5 berechnet.
Einfluss von Straßensteigungen
Die Straßensteigung wirkt sich in zweierlei Hinsicht auf die Schallemission des Fahrzeugs aus: zum einen auf die Fahrzeuggeschwindigkeit und damit auf die Emission von Roll- und Antriebsgeräuschen des Fahrzeugs; zum anderen auf die Motorleistung und die Motordrehzahl je nach eingelegtem Gang und damit auf die Emission von Antriebsgeräuschen des Fahrzeugs. In diesem Abschnitt wird nur der Einfluss auf die Antriebsgeräusche betrachtet, wobei eine gleichbleibende Geschwindigkeit angenommen wird.
Der Einfluss der Straßensteigung auf die Antriebsgeräusche wird durch den Korrekturterm ΔLWP,grad,m berücksichtigt, der von der Neigung s (in %), der Fahrzeuggeschwindigkeit νm (in km/h) und der Fahrzeugklasse m abhängig ist. Bei einem Verkehrsfluss mit Gegenverkehr muss der Fluss in zwei Komponenten aufgespalten und zur Hälfte für bergauf und zur Hälfte für bergab korrigiert werden. Der Korrekturterm wird allen Oktavbändern gleichmäßig angerechnet:
Für m = 1
|
| (2.2.13) |
Für m = 2
|
| (2.2.14) |
Für m = 3
|
| (2.2.15) |
Für m = 4
|
ΔLWP,grad,i,m = 4 = 0 | (2.2.16) |
Die Korrektur ΔLWP,grad,m schließt implizit den Einfluss einer Neigung auf die Geschwindigkeit ein.
2.2.5. Einfluss des Beschleunigens und Abbremsens von Fahrzeugen
Zur Berücksichtigung des Einflusses des Beschleunigens und Abbremsens vor bzw. nach Kreuzungen mit Verkehrsampeln und Kreisverkehren ist eine Korrektur wie nachfolgend beschrieben vorzunehmen.
Die Korrekturterme für Rollgeräusche, ΔLWR,acc,m,k, und Antriebsgeräusche, ΔLWP,acc,m,k, sind lineare Funktionen der Entfernung x (in m) der Punktquelle vom nächstgelegenen Schnittpunkt der entsprechenden Linienquelle mit einer anderen Linienquelle. Sie werden allen Oktavbändern gleichmäßig angerechnet:
|
| (2.2.17) |
|
| (2.2.18) |
Die Koeffizienten CR,m,k und CP,m,k sind abhängig von der Art des Straßenknotenpunkts k (k = 1 für eine Kreuzung mit Verkehrsampeln; k = 2 für einen Kreisverkehr) und werden für jede einzelne Fahrzeugklasse angegeben. Die Korrektur schließt den Einfluss der Geschwindigkeitsänderung beim Heranfahren an eine Kreuzung/einen Kreisverkehr bzw. beim Verlassen der Kreuzung/des Kreisverkehrs ein.
Zu beachten ist, dass bei einer Entfernung von |x| ≥ 100 m Folgendes gilt: ΔLWR,acc,m,k = ΔLWP,acc,m,k = 0.
2.2.6. Einfluss der Art der Straßenoberfläche
Allgemeine Grundsätze
Bei Straßenoberflächen mit akustischen Eigenschaften, die von denen der Referenzoberfläche abweichen, ist sowohl für die Rollgeräusche als auch für die Antriebsgeräusche ein Spektralkorrekturterm anzuwenden.
Für die Rollgeräuschemissionen wird der in Bezug auf die Straßenoberfläche anzuwendende Korrekturterm angegeben durch:
|
| (2.2.19) |
Hierbei gilt:
αi,m ist die Spektralkorrektur in dB bei Referenzgeschwindigkeit νref für Klasse m (1, 2 oder 3) und Spektralband i.
βm ist der Einfluss der Geschwindigkeit auf die Verringerung der Rollgeräusche bei Klasse m (1, 2 oder 3) und ist für alle Frequenzbänder identisch.
Für die Antriebsgeräuschemissionen wird der in Bezug auf die Straßenoberfläche anzuwendende Korrekturterm angegeben durch:
| ΔLWP,road,i,m = min{αi,m;0} | (2.2.20) |
Die Antriebsgeräusche werden durch absorbierende Oberflächen verringert, durch nicht absorbierende Oberflächen aber nicht verstärkt.
Einfluss der Gebrauchsdauer auf die Geräuscheigenschaften von Straßenoberflächen
Die Geräuschmerkmale von Straßenoberflächen variieren je nach Gebrauchsdauer und Instandhaltungszustand, wobei die Lautstärke im Zeitverlauf tendenziell zunimmt. Bei diesem Verfahren werden die Straßenoberflächenparameter so abgeleitet, dass sie für die akustische Leistung der jeweiligen Straßenoberfläche repräsentativ sind und für eine repräsentative Gebrauchsdauer gemittelt werden, wobei eine ordnungsgemäße Instandhaltung angenommen wird.
2.3. Eisenbahnlärm
2.3.1. Beschreibung der Quellen
Klassifizierung der Fahrzeuge
Definition von Fahrzeug und Zug
Für die Zwecke dieses Lärmberechnungsverfahrens wird ein Fahrzeug definiert als eine Teileinheit eines Zuges (typischerweise eine Lokomotive, ein Triebwagen, ein Reisezugwagen oder ein Güterwagen), die unabhängig bewegt und vom Rest des Zuges abgehängt werden können. Für Teileinheiten eines Zuges, die Teil einer nicht abtrennbaren Gruppe sind, können spezielle Umstände gelten, z.B. bei einem gemeinsamen Drehgestell. Für die Zwecke dieses Berechnungsverfahrens werden alle diese Teileinheiten zu einem einzigen Fahrzeug zusammengefasst.
Im Sinne dieses Berechnungsverfahrens besteht ein Zug aus einer Reihe von aneinander gekoppelten Fahrzeugen.
Tabelle [2.3.a] gibt die Terminologie zur Beschreibung der Fahrzeugtypen in der Quellendatenbank vor. Sie beinhaltet die relevanten Deskriptoren für die vollständige Klassifizierung der Fahrzeuge. Diese Deskriptoren entsprechen den Eigenschaften des Fahrzeugs, die die akustische gerichtete Schallleistung je Meter Länge der modellierten Ersatzlinienquelle beeinflussen.
Die Anzahl der Fahrzeuge je Typ ist für jeden einzelnen Gleisabschnitt für jeden der Zeiträume, die bei der Lärmkartierung zu berücksichtigen sind, zu bestimmen. Sie ist als mittlere Fahrzeugzahl je Stunde anzugeben, die ermittelt wird, indem aus der Gesamtzahl der in einem bestimmten Zeitraum vorbeifahrenden Fahrzeuge und der Länge dieses Zeitraums in Stunden der Quotient gebildet wird (z.B. 24 Fahrzeuge in vier Stunden bedeutet sechs Fahrzeuge pro Stunde). Alle Fahrzeugtypen, die den jeweiligen Gleisabschnitt passieren, sind einzubeziehen.
Tabelle [2.3.a] Klassifizierung und Deskriptoren für Schienenfahrzeuge
| Stelle | 1 | 2 | 3 | 4 |
| Deskriptor | Fahrzeugtyp | Anzahl der Achsen je Fahrzeug | Bremsentyp | Maßnahmen in Bezug auf die Räder |
| Erläuterung des Deskriptors | Ein Buchstabe, der den Typ beschreibt | Die tatsächliche Anzahl der Achsen | Ein Buchstabe, der den Bremsentyp beschreibt | Ein Buchstabe, der die Art der Maßnahme zur Lärmminderung beschreibt |
| Mögliche Deskriptoren | h
Hochgeschwindigkeitsfahrzeug | 1 | c
Grauguss-Bremsklotzsohle | n
keine Maßnahme |
| m
Personentriebwagen | 2 | k
Klotzbremse mit Bremsklotzsohlen aus Verbundstoff oder Sintermetall | d
Radabsorber | |
| p
Reisezugwagen | 3 | n
nicht klotzgebremst, wie etwa Scheiben-, Trommel- oder Magnetbremsen | s
Schallschürzen | |
| c
Straßenbahn oder Stadtbahn, Wagen mit und ohne eigenen Antrieb | 4 | o
andere | ||
| d
Diesellok | usw. | |||
| e
Elektrolok | ||||
| a
alle arttypischen Güterfahrzeuge | ||||
| o
sonstige (d. h. Wartungsfahrzeuge usw.) |
Klassifizierung von Gleisen und des Schienenoberbaus
Die bestehenden Gleise unterscheiden sich, weil verschiedene Elemente zu ihren akustischen Eigenschaften beitragen und diese charakterisieren. Eine Übersicht über die bei diesem Verfahren verwendeten Schienentypen wird in Tabelle [2.3.b] gegeben. Einige Parameter haben einen großen Einfluss auf die akustischen Eigenschaften, andere hingegen kaum. Die Lärmemission von Eisenbahnen wird im Allgemeinen von folgenden Faktoren beeinflusst: Schienenrauheit, Steifheit der Zwischenlagen, Oberbau, Schienenstöße und Radius des Gleisabschnittes. Alternativ können die allgemeinen Gleismerkmale definiert werden, wobei in diesem Fall die Schienenrauheit und die Gleisabklingrate (Track Decay Rate) gemäß ISO 3095 die beiden akustisch wesentlichen Parameter sind; hinzu kommt der Bogenhalbmesser der Strecke.
Ein Gleisabschnitt wird als Teil eines einzelnen Gleises auf einer Eisenbahnstrecke oder einem Bahnhof oder einem Betriebsbahnhof definiert, auf dem sich die physikalischen Eigenschaften und Grundbestandteile des Gleises nicht ändern.
Laut Tabelle [2.3.b] ist zur Beschreibung der Gleisarten in der Quellendatenbank die folgende Terminologie zu verwenden.
| Stelle | 1 | 2 | 3 | 4 | 5 | 6 |
| Deskriptor | Oberbau | Schienenrauheit | Art der Zwischenlagen | Zusatzmaßnahmen | Schienenstöße | Bogen |
| Erläuterung des Deskriptors | Art des Oberbaus | Indikator für Rauheit | Gibt einen Hinweis auf die 'dynamische' Steifigkeit | Ein Buchstabe zur Beschreibung der Schallschutzmaßnahmen | Vorhandensein von Stößen und Zwischenräumen | Angabe zum Radius eines Bogens in m |
| Zulässige Codes | B
Schotterbettung | E
Guter Wartungszustand, sehr glatt | S
Weich (150-250 MN/m) | N
Keine | N
Keine | N
Gerades Gleis |
| S
Feste Fahr bahn | M
Normaler Wartungszustand | M
Mittel (250 bis 800 MN/m) | D
Schienenstegdämpfer | S
Einzelne(r) Stoß oder Weiche | L
Niedrig (1.000-500 m) | |
| L
Brücke mit Schotterbett | N
Kein guter Wartungszustand | H
Hart (800-1.000 MN/m) | B
Niedrige Schutzwand | D
Zwei Stöße oder Weichen je 100 m | M
Mittel (Weniger als 500 m und mehr als 300 m) | |
| N
Schotterlose Brücke | B
Keine Wartung und schlechter Zustand | A
Absorberplatte auf fester Fahrbahn | M
Mehr als zwei Stöße oder Weichen je 100 m | H
Hoch (Weniger als 300 m) | ||
| T
straßenbündiger Bahnkörper | E
Eingelassenes Gleis | |||||
| O
Andere | O
Andere |
Anzahl und Position der Ersatzschallquellen
Abbildung [2.3.a] Position der Ersatzschallquellen
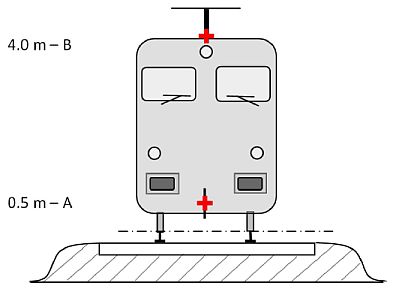
Die verschiedenen Ersatzlinienquellen werden in unterschiedlichen Höhen und in der Mitte des Gleises platziert. Alle Höhen beziehen sich auf die tangential zu den beiden oberen Oberflächen der beiden Schienen verlaufende Ebene.
Die Ersatzschallquellen umfassen unterschiedliche technische Quellen (Index p). Sie werden je nach der Art ihrer Entstehung in verschiedene Kategorien unterteilt: 1) Rollgeräusche (dazu gehören nicht nur Schwingungen des Gleises und des Oberbaus sowie Schwingungen der Räder, sondern gegebenenfalls auch Geräusche der Aufbauten von Güterfahrzeugen); 2) Antriebsgeräusche; 3) aerodynamische Geräusche; 4) Stoßgeräusche (von Kreuzungen, Weichen und Schienenstößen); 5) Bremsgeräusche und 6) Geräusche aufgrund zusätzlicher Einflussfaktoren wie Brücken und Viadukte.
- Die Rauheit der Räder und der Fahrflächen bewirkt über die drei Übertragungswege zu den abstrahlenden Oberflächen (Schienen, Räder und Aufbauten) die Rollgeräusche. Die Zuordnung erfolgt auf Höhe h = 0,5 m (abstrahlende Oberflächen A), um den Anteil der Fahrbahn, einschließlich der Effekte der Fahrbahnoberfläche und insbesondere fester Fahrbahnen (gemäß dem Ausbreitungsteil), den Anteil der Räder und (bei Güterwagen) den Anteil der Fahrzeugaufbauten an der Geräuscherzeugung abzubilden.
- Die Höhe der äquivalenten Quellen für Antriebsgeräusche liegt in Abhängigkeit von der physischen Position der betreffenden Komponente im Bereich von 0,5 m (Quelle A) und 4,0 m (Quelle B). Quellen wie Getriebe und Elektromotoren befinden sich oft auf der Achsenhöhe von 0,5 m (Quelle A). Lüftungsgitter und Lüftungsschlitze können sich auf unterschiedlichen Höhen befinden; bei Dieselfahrzeugen befindet sich der Auspuff häufig auf der Dachhöhe von 4,0 m (Quelle B). Andere Antriebsquellen wie Gebläse oder Dieselmotorblöcke können sich auf einer Höhe von 0,5 m (Quelle A) oder 4,0 m (Quelle B) befinden.
Liegt die genaue Quellenhöhe zwischen den Modellhöhen, wird die Schallenergie proportional auf die nächstgelegenen Quellenhöhen verteilt.
Aus diesem Grund sind für das Verfahren zwei Quellenhöhen vorgesehen, eine bei 0,5 m (Quelle A) und eine bei 4,0 m (Quelle B), wobei die jeweils mit einer Höhe verbundene äquivalente Schallleistung zwischen den beiden Höhen je nach der konkreten Anordnung der Quellen an der Einheit aufgeteilt wird. - Die aerodynamischen Geräuscheffekte sind mit der Quelle bei 0,5 m (Abdeckungen und Abschirmungen, Quelle A) und der Quelle bei 4,0 m (Modellierung aller Dachaggregate und der Stromabnehmer, Quelle B) verbunden. Die Wahl von 4,0 m für Stromabnehmereffekte ist bekanntermaßen ein einfaches Modell und muss sorgfältig geprüft werden, wenn die geeignete Höhe für Lärmschutzwände gefunden werden soll.
- Stoßgeräusche sind mit der Quelle bei 0,5 m (Quelle A) verbunden.
- Bremsgeräusche sind mit den Quellen bei 0,5 m (Quelle A) verbunden.
- Brückendröhnen ist mit der Quelle bei 0,5 m (Quelle A) verbunden.
2.3.2. Schallleistungspegel 21
Allgemeine Gleichungen
Einzelnes Fahrzeug
Das Modell für den Schienenverkehrslärm beschreibt - analog zum Straßenverkehrslärm - die Schallemission einer bestimmten Kombination von Fahrzeugtyp und Fahrbahntyp, die eine Reihe von Voraussetzungen erfüllt, die in der Fahrzeug- und Fahrbahnklassifizierung in Bezug auf die Schallleistung für jedes einzelne Fahrzeug beschrieben sind (LW,0).
Verkehrsfluss
Die Schallemission eines Verkehrsflusses auf jedem Gleis ist durch jeweils zwei Linienquellen darzustellen, die durch ihre gerichtete Schallleistung je Meter je Frequenzband gekennzeichnet sind. Dies entspricht der Summe der Schallemissionen aller im Verkehrsfluss vorbeifahrenden Fahrzeuge, wobei im speziellen Fall stehender Fahrzeuge die Zeit berücksichtigt wird, die die Fahrzeuge im untersuchten Gleisabschnitt verbringen.
Die gerichtete Schallleistung je Meter je Frequenzband aller auf jedem Gleisabschnitt mit dem Oberbau (j) vorbeifahrenden Fahrzeuge wird ermittelt
- für jedes Frequenzband (i),
- für jede gegebene Quellenhöhe (h) (für Quellen bei 0,5 m h = 1 und bei 4,0 m h = 2),
und ist die energetische Summe der Beiträge aller Fahrzeuge, die den speziellen j-ten Gleisabschnitt befahren. Der jeweilige Beitrag geht auf Folgendes zurück:
- alle Fahrzeugtypen (t),
- mit ihren jeweiligen Geschwindigkeiten (s),
- mit ihren jeweiligen Betriebszuständen (konstante Geschwindigkeit) (c),
- die einzelnen physikalischen Quellen (Roll-, Stoß-, Quietsch-, Brems- und Antriebsgeräusche, aerodynamische und andere Geräusche wie etwa Brückendröhnen) (p).
Zur Berechnung der gerichteten Schallleistung je Meter (Eingabe in das Ausbreitungsmodell) ausgehend vom durchschnittlichen Verkehrsmix auf dem j-ten Gleisabschnitt wird folgende Gleichung verwendet:
|
| (2.3.1) |
Hierbei gilt:
| Tref | = Referenzzeitraum, für den der durchschnittliche Verkehr untersucht wird, |
| x | = Gesamtzahl vorhandener Kombinationen von i, t, s, c und p für jeden j-ten Gleisabschnitt, |
| t | = Index der Fahrzeugtypen im j-ten Gleisabschnitt, |
| s | = Index der Zuggeschwindigkeit: Es gibt so viele Indizes wie durchschnittliche Zuggeschwindigkeiten im j-ten Gleisabschnitt, |
| c | = Index der Betriebsbedingungen: 1 (für konstante Geschwindigkeit), 2 (Leerlauf), |
| p | = Index der physikalischen Quellen: 1 (Roll- und Stoßgeräusche), 2 (Kurvenkreischen), 3 (Antriebsgeräusche und Aggregatgeräusche), 4 (aerodynamische Geräusche), 5 (sonstige Geräusche), |
| LW',eq,line,x | = x-te gerichtete Schallleistung je Meter für eine Linienquelle einer Kombination von t, s, c und p in jedem j-ten Gleisabschnitt. |
Wenn ein stetiger Fluss von Q Fahrzeugen pro Stunde mit einer mittleren Geschwindigkeit ν angenommen wird, dann ist im Durchschnitt zu jedem Zeitpunkt eine äquivalente Anzahl von Q/ν-Fahrzeugen je Längeneinheit des Schienenabschnitts vorhanden. Die Schallemission des Fahrzeugflusses in Form der gerichteten Schallleistung je Meter LW'2,eq,line (ausgedrückt in dB/m (re 10-12 W)) wird integriert durch:
|
| (2.3.2) |
Hierbei gilt:
- Q ist die durchschnittliche Anzahl von Fahrzeugen je Stunde im j-ten Gleisabschnitt für den Fahrzeugtyp t, die mittlere Zuggeschwindigkeit s und den Betriebszustand c;
- v ist deren Geschwindigkeit [km/h] im j-ten Gleisabschnitt für Fahrzeugtyp t und die mittlere Zuggeschwindigkeit s;
- LW,0,dir ist der Pegel der gerichteten Schallleistung des jeweiligen Geräuschs (Roll-, Stoß-, Quietsch-, Brems- und Antriebsgeräusche, aerodynamische und andere Geräusche) eines einzelnen Fahrzeugs in den Richtunge ψ und Φ, bezogen auf die Fahrtrichtung (siehe Abbildung [2.3.b]).
Im Falle einer stationären Quelle, wie etwa bei einem Betriebshalt, wird angenommen, dass das Fahrzeug für eine Gesamtzeit Tidle an einem Ort innerhalb eines Gleisabschnitts mit der Länge L verbleibt. Deshalb wird mit dem Referenzzeitraum Tref zur Einschätzung der Lärmbelastung (z.B. 12 Stunden, 4 Stunden, 8 Stunden) die gerichtete Schallleistung je Längeneinheit auf diesem Gleisabschnitt wie folgt definiert:
|
| (2.3.4) |
Generell errechnet sich die gerichtete Schallleistung für jede spezifische Quelle wie folgt:
| LW,0,dir,i(ψ,Φ) = LW,0,i + ΔLW,dir,vert,i + ΔLW,dir,hor,i | (2.3.5) |
Hierbei gilt:
- ΔLW,dir,vert,i ist die Korrekturfunktion für die vertikale Richtwirkung (dimensionslos) von ψ (Abbildung [2.3.b]),
- ΔLW,dir,hor,i ist die Korrekturfunktion für die horizontale Richtwirkung (dimensionslos) von Φ (Abbildung [2.3.b]).
Dabei ist LW,0,dir,i(ψ,Φ) nach der Ableitung in Terzbänder in Oktavbändern auszudrücken, indem die betreffenden Terzbänder energetisch zu dem entsprechenden Oktavband addiert werden.
Abbildung [2.3.b] Geometrische Definition
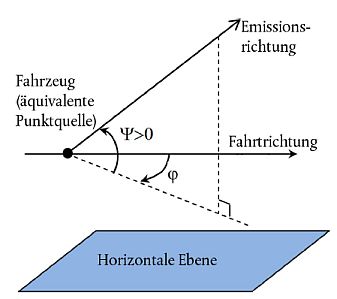
Die horizontale und vertikale Richtwirkung der Schallquellen wird für die Berechnung durch (entsprechende) Zuschläge auf die Schallleistung je 1 m Gleis LW',tot,dir,i berücksichtigt.
Für jede Kombination aus Fahrzeug, Strecke, Geschwindigkeit und Fahrt werden mehrere LW,0,dir,i(ψ, Φ) berÌcksichtigt:
- für ein Terzband (i),
- für jeden Gleisabschnitt (j),
- Quellenhöhe (h) (für Quellen bei 0,5 m h = 1 und bei 4,0 m h = 2),
- Richtwirkung (d) der Quelle.
Je Kombination aus Fahrzeug, Strecke, Geschwindigkeit und Betriebsbedingung wird für jeden Gleisabschnitt und jede Quellhöhe h = 1 und h = 2 unter Berücksichtigung der Richtwirkung LW,0,dir,i(ψ,Φ) ermittelt.
Rollgeräusche
Die Beiträge des Fahrzeuges und des Gleises an den Rollgeräuschen werden in die folgenden vier Hauptelemente unterteilt: Radrauheit, Schienenrauheit, Fahrzeugtransferfunktion auf Räder und Aufbauten (Behälter) sowie Schienentransferfunktion. Der Fahrzeuganteil und der Fahrbahnanteil an den Rollgeräuschen werden in die folgenden vier Hauptelemente unterteilt: Radrauheit, Schienenrauheit, Fahrzeugtransferfunktion auf die Räder und die Aufbauten (Behältnisse) und Transferfunktion von den Schienen. Rad- und Schienenrauheit bilden die Ursache für die Anregung von Schwingungen am Kontaktpunkt zwischen Schiene und Rad; bei den Transferfunktionen handelt es sich um zwei empirische oder modellierte Funktionen, die das gesamte komplexe Phänomen der Entstehung mechanischer Schwingungen und von Schall an den Oberflächen des Rades, der Schiene, der Schwelle und des Gleisunterbaus darstellen. Diese Unterteilung spiegelt den physikalischen Tatbestand wider, dass die Rauheit auf einer Schiene die Schwingung der Schiene anregen kann, aber auch die Schwingung des Rades und umgekehrt anregt. Bliebe einer dieser vier Parameter unberücksichtigt, so würde der Zusammenhang, der mit der Klassifizierung von Schienen und Zügen hergestellt wird, aufgehoben.
Rad- und Schienenrauheit
Rollgeräusche werden hauptsächlich durch Schienen- und Radrauheit im Wellenlängenbereich 5-500 mm angeregt.
Definition
Die Rauheit Lr wird definiert als der zehnfache Zehnerlogarithmus des Verhältnisses aus dem Quadrat des Effektivwertes r2 der Rauheit der Lauffläche einer Schiene oder eines Rades in Bewegungsrichtung
(Längsrichtung) gemessen in pm über eine bestimmte Schienenlänge oder den gesamten Raddurchmesser und des Quadrats des Referenzwertes r20:
|
| (2.3.6) |
Hierbei gilt:
r0 = 1 pm,
r = Effektivwert (rms) der Differenz der vertikalen Verdrängung der Kontaktoberfläche zum Mittelwert.
Die Rauheit Lr wird typischerweise als Spektrum der Wellenlänge λ bestimmt und muss in ein Frequenzspektrum ƒ = ν/λ konvertiert werden, wobei ƒ die Mittenfrequenz eines bestimmten Terzbands in Hz, λ die Wellenlänge in m und ν die Zuggeschwindigkeit in m/s ist. Das Rauheitsspektrum als Funktion der Frequenz verschiebt sich bei unterschiedlichen Geschwindigkeiten entlang der Frequenzachse. Üblicherweise müssen nach einer Konvertierung in das Frequenzspektrum mittels der Geschwindigkeit neue Terzbandwerte bestimmt werden, indem der Mittelwert von zwei entsprechenden Terzbändern im Wellenlängenbereich gebildet wird. Um das gesamte Frequenzspektrum der effektiven Rauheit entsprechend der zugehörigen Zuggeschwindigkeit zu bestimmen, ist der Mittelwert der beiden im Wellenlängenbereich definierten entsprechenden Terzbänder energetisch und proportional zu ermitteln.
Die Schienenrauheit (schienenseitige Rauheit) für das i-te Wellenzahlband wird definiert als Lr,TR,i.
Analog wird die Radrauheit (fahrzeugseitige Rauheit) für das i-te Wellenzahlband definiert als Lr,VEH,i
Die effektive Gesamtrauheit für das Wellenzahlband i (LR,tot,i) wird zur Berücksichtigung der Filterwirkung der Kontaktfläche zwischen Schiene und Rad definiert als die Energiesumme von Schienen- und Radrauheit zuzüglich des Kontaktfilters A3(λ); die Angabe erfolgt in dB:
|
| (2.3.7) |
wobei er als Funktion des i-ten Wellenzahlbands entsprechend der Wellenlänge λ ausgedrückt wird.
Der Kontaktfilter ist abhängig vom Schienen- und Radtyp sowie der Achslast.
Im Verfahren ist die effektive Gesamtrauheit für den j-ten Gleisabschnitt und jeden t-ten Fahrzeugtyp bei seiner entsprechenden Geschwindigkeit
ν zu verwenden.
Fahrzeug-, Gleis- und Aufbautentransferfunktion
Es werden drei geschwindigkeitsunabhängige Transferfunktionen LH,TR,i LH,VEH,i und LH,VEH,SUP,i bestimmt: die erste für jeden j-ten Gleisabschnitt und die beiden anderen für jeden t-ten Fahrzeugtyp. Sie setzen den Grad der effektiven Gesamtrauheit in Bezug zur Schallleistung der Schienen, der Räder bzw. der Aufbauten.
Der Aufbautenanteil wird nur für Güterwagen und deshalb nur für den Fahrzeugtyp "a" berücksichtigt.
Somit wird bei den Rollgeräuschen der Beitrag der Schiene und des Fahrzeugs durch diese Transferfunktionen und die effektive Gesamtrauheit vollständig beschrieben. Bei Zügen im Leerlauf (Betriebshalt) werden keine Rollgeräusche berücksichtigt.
Für die Schallleistung je Fahrzeug werden die Rollgeräusche auf Achsenhöhe berechnet; Ausgangswerte dafür sind die effektive Gesamtrauheit LR,TOT,i als Funktion der Fahrzeuggeschwindigkeit ν, die Schienen-, Fahrzeug- und Aufbautentransferfunktionen LH,TR,i, LH,VEH,i bzw. LH,VEH,SUP,i sowie die Gesamtachsenzahl Na:
für h = 1:
| LW,0,TR,i = LR,TOT,i + LH,TR,i + 10 x lg(Na) | dB | (2.3.8), |
| LW,0,VEH,i = LR,TOT,i + LH,VEH,i + 10 x lg(Na) | dB | (2.3.9), |
| LW,0,VEHSUP,i = LR,TOT,i + LH,VEHSUP,i + 10 x lg(Na) | dB | (2.3.10), |
wobei Na die Anzahl der Achsen je Fahrzeug für den t-ten Fahrzeugtyp ist.
Abbildung [2.3.c] Schema der Verwendung der verschiedenen Definitionen für Rauheit und Transferfunktionen
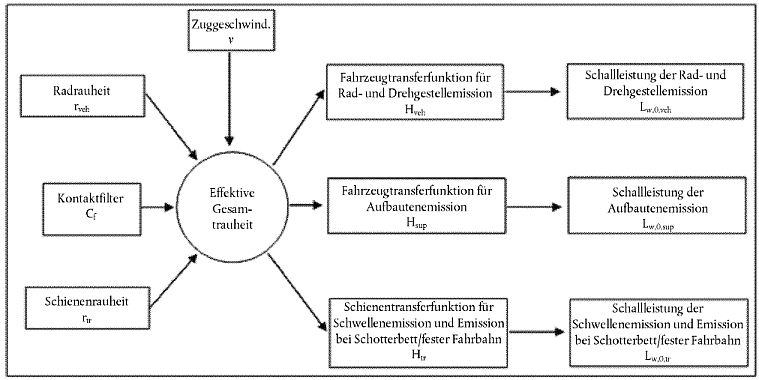
Zum Ausgleich des potenziellen Fehlers infolge der Vereinfachung der Definition der Rollgeräusche, der Definition der Bremsgeräusche und der Definition der Stoßgeräusche auf Kreuzungen und Weichen ist zur Ermittlung der effektiven Gesamtrauheit und damit der Schallleistung der Fahrzeuge eine Mindestgeschwindigkeit von 50 km/h (30 km/h nur bei Straßenbahnen und Stadtbahnen) (diese Geschwindigkeit berührt nicht die Berechnung des Fahrzeugstroms) zu verwenden.
Stoßgeräusche (Kreuzungen, Weichen und Schienenstöße)
Stoßgeräusche können durch Kreuzungen, Weichen und Schienenstöße verursacht werden. Sie können unterschiedlich stark sein und die Rollgeräusche dominieren. Stoßgeräusche sind für Stoßlückengleise zu berücksichtigen. Für Stoßgeräusche aufgrund von Weichen, Kreuzungen und Schienenstößen in Gleisabschnitten mit einer Geschwindigkeit von unter 50 km/h (30 km/h nur für Straßenbahnen und Stadtbahnen) ist auf die Modellierung zu verzichten, da die Mindestgeschwindigkeit von 50 km/h (30 km/h nur für Straßenbahnen und Stadtbahnen) verwendet wird, um mehr Einflüsse gemäß der Beschreibung im Abschnitt "Rollgeräusche" einzubeziehen. Unnötig ist die Modellierung von Stoßgeräuschen auch bei der Fahrbedingung c = 2 (Leerlauf).
Stoßgeräusche werden in den Term für Rollgeräusche einbezogen, indem eine ergänzende fiktive Rauheit für Stöße zur fiktiven Gesamtrauheit auf jedem spezifischen j-ten Gleisabschnitt (energetisch) hinzuaddiert wird, auf dem sie vorhanden sind. In diesem Fall ist anstelle von LR,TOT,i ein neuer Term LR,TOT,i + IMPACT,i zu verwenden, der dann folgende Form hat:
|
| dB | (2.3.11) |
LR,IMPACT,i ist ein Terzbandspektrum (als Funktion der Frequenz). Um dieses Frequenzspektrum zu bestimmen, ist ein Spektrum als Funktion der Wellenlänge λ gegeben und wird dann in das verlangte Spektrum als Funktion der Frequenz mittels der Formel λ = ν/ƒ konvertiert, wobei ƒ die Mittenfrequenz eines Terzbandes in Hz und v die s-te Fahrzeuggeschwindigkeit des t-ten Fahrzeugtyps in m/s ist.
Stoßgeräusche sind abhängig von der Schwere und Anzahl der Stöße je Längeneinheit bzw. der Schienenstoßdichte; wenn also mehrfach Stoßgeräusche gegeben sind, ist die in der Gleichung zu verwendende Rauheit für Stoßgeräusche wie folgt zu berechnen:
|
| dB | (2.3.12), |
wobei LR,IMPACT-SINGLE,i die für einen einzigen Stoß angegebene Rauheit für Stoßgeräusche und die Schienenstoßdichte ist.
Die standardmäßige Rauheit für Stoßgeräusche wird für eine Schienenstoßdichte von nl = 0,01 m-1 angegeben, was einem Schienenstoß pro 100 m Gleis entspricht. Bei einer anderen Anzahl von Schienenstößen erfolgt eine Näherung durch Korrektur der Schienenstoßdichte nl. Zu beachten ist, dass bei der Modellierung des Layouts und der Segmentierung der Fahrstrecke die Schienenstoßdichte zu berücksichtigen ist, d. h. für einen Gleisbereich mit mehr Schienenstößen könnte es notwendig sein, ein gesondertes Quellensegment zu verwenden. Der LW,0 des Schienen-, Rad-/Drehgestell- und Aufbautenanteils wird für +/- 50 m vor und nach dem Schienenstoß mittels LR,mPACTi erhöht. Im Falle einer Vielzahl von Schienenstößen wird die Erhöhung auf die Strecke zwischen -50 m vor dem,ersten Schienenstoß und + 50 m nach dem letzten Schienenstoß erweitert.
Die Anwendbarkeit dieser Schallleistungsspektren ist in der Regel vor Ort zu überprüfen.
Für Stoßlückengleise ist ein Standardwert nl von 0,01 anzuwenden.
Kreischen
Das Kurvenkreischen ist eine besondere Quelle, die nur für Bogen relevant und somit örtlich begrenzt ist. Kurvenkreischen ist generell abhängig von der Bogenkrümmung, den Reibungsbedingungen, der Zuggeschwindigkeit sowie der Rad-Schiene-Geometrie und Dynamik. Da es in signifikantem Maße auftreten kann, ist eine angemessene Beschreibung notwendig. Für Stellen, an denen Kurvenkreischen auftritt - in der Regel in Kurven und an den Zungenvorrichtungen von Weichen - müssen der Schallleistung der Quelle geeignete Schallleistungsspektren für die zusätzliche Geräuschemission hinzugefügt werden. Die zusätzliche Geräuschemission kann für die einzelnen Arten von Fahrzeugen spezifisch sein, da bestimmte Rad- und Drehgestelltypen deutlich weniger anfällig für Kreischen sind als andere. Sind Messungen der zusätzlichen Geräuschemissionen verfügbar, die dem stochastischen Auftreten von Kreischen hinreichend Rechnung tragen, so können diese verwendet werden.
Liegen keine geeigneten Messungen vor, kann ein einfacher Ansatz gewählt werden. Bei diesem Ansatz ist das Kreischgeräusch zu berücksichtigen, indem den Schallleistungsspektren der Rollgeräusche für alle Frequenzen die folgenden Werte für die zusätzliche Geräuschemission hinzuaddiert werden.
| Zug | 5 dB für Kurven mit 300 m < R ≤ 500 m und ltrack ≥ 50 m 8 dB für Kurven mit R ≤ 300 m und ltrack ≥ 50 m 8 dB für Weichen mit R ≤ 300 m 0 dB in sonstigen Fällen |
| Straßenbahn | 5 dB für Kurven und Weichen mit R ≤ 200 m 0 dB in sonstigen Fällen |
Dabei ist ltrack die Länge des Gleises entlang der Kurve und R der Kurvenradius.
Die Anwendbarkeit dieser Schallleistungsspektren bzw. dieser Werte für die zusätzliche Geräuschemission ist in der Regel vor Ort zu überprüfen, insbesondere bei Straßenbahnen und an Orten, an denen in Kurven oder Weichen Maßnahmen gegen Kreischen ergriffen werden.
Antriebsgeräusche
Die Antriebsgeräusche weisen im Allgemeinen zwar für die typischen Betriebsbedingungen wie gleichbleibende Geschwindigkeit, Abbremsen, Beschleunigen und Stand eine entsprechende Spezifik auf, doch werden nur die beiden Bedingungen "gleichbleibende Geschwindigkeit" (dies gilt auch beim Abbremsen und Beschleunigen der Züge) und "Stand" modelliert. Modelliert wird nur die Schallstärke der Quellen beim Maximum der Leistungsbedingungen, was zu den Größen LW,0,const,i = LW,0,idling,i führt. Ferner entspricht LW,0,idling,i dem Anteil aller physischen Quellen eines bestimmten Fahrzeugs, die einer bestimmten Höhe zuzuschreiben sind (siehe 2.3.1).
LW,0,idling,i wird als statische Schallquelle im Leerlaufzustand für die Dauer des Betriebshalts ausgedrückt und ist als feste Punktquelle entsprechend der Beschreibung im Abschnitt "Industrie- und Gewerbelärm" modelliert zu verwenden. Sie ist nur zu berücksichtigen, wenn sich Züge länger als 0,5 Stunden im Stand (Betriebshalt) befinden.
Diese Mengen können entweder durch Messung aller Quellen in den verschiedenen Betriebszuständen ermittelt werden, oder die Teilquellen können einzeln charakterisiert werden, und zwar durch Bestimmung ihrer Parameterabhängigkeit und relativen Stärke. Dies kann durch Messungen an einem stehenden Fahrzeug geschehen, indem gemäß ISO 3095:2005 die Drehzahl verändert wird. Gegebenenfalls müssen mehrere Antriebsgeräuschquellen charakterisiert werden, die nicht unmittelbar von der Fahrzeuggeschwindigkeit abhängig sind:
- Geräusche von Antrieb, wie etwa Dieselmotoren (einschließlich Einlass, Auspuff und Motorblock), Getriebe, Elektrogeneratoren, abhängig vor allem von der Motordrehzahl (U/min), und elektrische Schallquellen wie Wandler, bei denen überwiegend Lastabhängigkeit besteht;
- Geräusche von Gebläsen und Kühlsystemen je nach Drehzahl des Ventilators (U/min); in einigen Fällen sind Gebläse direkt an die Antriebswelle gekoppelt;
- intermittierende Schallquellen wie Kompressoren, Ventile und andere Aggregate mit charakteristischer Betriebsdauer und der sich daraus ergebenden betriebszyklusbedingten Korrektur der Schallemission.
Da sich jede dieser Quellen in jedem Betriebszustand anders verhalten kann, sind die Antriebsgeräusche entsprechend zu spezifizieren. Die Schallstärke der Quellen wird mit Messungen unter kontrollierten Bedingungen bestimmt. Bei Lokomotiven weist die Belastung tendenziell eine größere Schwankungsbreite auf, da die Zahl der angekuppelten Eisenbahnwagen und damit die Lokomotivleistung sehr unterschiedlich sein können, während bei festen Zugzusammenstellungen wie Elektro- und Dieseltriebzügen sowie Hochgeschwindigkeitszügen die Leistung klarer definiert ist.
Es wird keine Vorabzuweisung der Schallleistung der Quelle zur Höhenposition der Quelle vorgenommen, da sich diese Entscheidung nach dem konkret zu bewertenden Schall und Fahrzeug richtet. Die Modellierung erfolgt an Quelle A (h = 1) und an Quelle B (h = 2).
Aerodynamische Geräusche
Aerodynamisch angeregte Geräusche sind nur bei hohen Geschwindigkeiten über 200 km/h von Belang, weshalb zunächst überprüft werden sollte, ob sie für die Anwendung tatsächlich erforderlich sind. Wenn die Rollgeräuschrauheit und die Transferfunktionen bekannt sind, können sie auf höhere Geschwindigkeiten extrapoliert werden, und es kann ein Vergleich mit vorhandenen Hochgeschwindigkeitsdaten angestellt werden, um nachzuprüfen, ob durch aerodynamisch angeregte Geräusche höhere Pegel erzeugt werden. Liegen die Zuggeschwindigkeiten in einem Netz über 200 km/h, jedoch nicht über 250 km/h, können die aerodynamischen Geräusche in Abhängigkeit von der Fahrzeugkonstruktion in einigen Fällen unberücksichtigt bleiben.
Der Anteil aerodynamischer Geräusche wird als Funktion der Geschwindigkeit angegeben:
|
| dB | für h = 1 | (2.3.13) |
|
| dB | für h = 2 | (2.3.14) |
Hierbei gilt:
ν0 ist eine Geschwindigkeit, bei der aerodynamische Geräusche dominant sind und die auf 300 km/h festgelegt ist.
LW,0,1,i ist eine Referenzschallleistung, die an zwei oder mehr Messpunkten für Quellen ermittelt wird, deren Höhe bekannt ist, beispielsweise das erste Drehgestell.
LW,0,2,i ist eine Referenzschallleistung, die an zwei oder mehr Messpunkten für Quellen ermittelt wird, deren Höhe bekannt ist, beispielsweise die Stromabnehmeraussparung.
α1,i ist ein Koeffizient, der an zwei oder mehr Messpunkten für Quellen ermittelt wird, deren Höhe bekannt ist, beispielsweise das erste Drehgestell.
α2,i ist ein Koeffizient, der an zwei oder mehr Messpunkten für Quellen ermittelt wird, deren Höhe bekannt ist, beispielsweise die Stromabnehmeraussparung.
Richtverhalten der Quellen
Die horizontale Richtwirkung ΔLW,dir,hor,i in dB wird in der horizontalen Ebene bestimmt und kann als Dipol für Roll-, Stoß- (Schienenstöße usw.), Kreisch-, Brems-, Gebläse- und aerodynamische Einflüsse angesehen werden, die für jedes i-te Frequenzband angegeben werden durch:
| ΔLW,dir,hor,i = 10 x lg(0,01 + 0,99 · sin2Φ) | (2.3.15) |
Brückendröhnen wird an der Quelle A (h = 1) modelliert, für die eine Rundumrichtwirkung angenommen wird.
Die vertikale Richtwirkung Δ LW,dir,ver,i in dB wird in der vertikalen Ebene für Quelle A (h = 1) als Funktion der Mittelbandfrequenz fc,i jedes einzelnen i-ten Frequenzbands angegeben. Dabei gilt Folgendes:
| Für 0 < ψ < π/2 ist
für -π/2 < ψ < =0 ist LW,dir,ver,i = 0 |
Für Quelle B (h = 2) gilt für die aerodynamischen Einflüsse:
| ΔLW,dir,ver,i = 10 x lg(cos2ψ) | für ψ < 0 | (2.3.17) |
ΔLW,dir,ver,i = 0 in allen anderen Fällen
Die Richtwirkung ΔLdir,ver,i wird für die Quelle B (h = 2) hinsichtlich sonstiger Einflüsse nicht berücksichtigt, da für diese Quellen an dieser Position eine Rundumrichtwirkung angenommen wird.
2.3.3. Zusätzliche Einflüsse 21
Korrektur um den Wert der baulichen Abstrahlung (Brücken und Viadukte)
Befindet sich der Gleisabschnitt auf einer Brücke, so müssen die zusätzlichen Geräusche berücksichtigt werden, die durch die Schwingung der Brücke infolge der Anregung durch die Anwesenheit des Zuges erzeugt werden. Das Brückendröhnen wird als zusätzliche Quelle modelliert, deren Schallleistung pro Fahrzeug wie folgt angegeben wird:
|
LW,0, bridge,i = LR,TOT,i + LH,bridge,i + 10 x 1g(Na) Db |
Dabei ist LH,bridge,i die Brückentransferfunktion. Das Brückendröhnen LW,0,bridge,i stellt nur den durch die Brückenkonstruktion abgestrahlten Schall dar. Das Rollgeräusch eines Fahrzeugs auf der Brücke wird anhand der Gleichungen (2.3.8) bis (2.3.10) berechnet, indem die Schienentransferfunktion gewählt wird, die dem auf der Brücke vorhandenen Gleissystem entspricht. Barrieren an den Kanten der Brücke werden in der Regel nicht berücksichtigt.
Korrektur um weitere eisenbahnbezogene Schallquellen
Verschiedene Quellen wie Betriebsbahnhöfe, Be-/Entladebereiche, Bahnhöfe/Haltestellen, Klingeln, Lautsprecher auf Bahnhöfen bzw. an Haltestellen usw. können vorhanden sein und werden dem Eisenbahnlärm zugeordnet. Diese Quellen sind als Industrie-/Gewerbelärmquellen (feste Schallquellen) zu behandeln und erforderlichenfalls gemäß dem nachfolgenden Abschnitt "Industrie und Gewerbelärm" zu modellieren.
2.4. Industrie- und Gewerbelärm
2.4.1. Beschreibung der Quellen 21
Klassifizierung der Quellenarten (Punkt, Linie, Fläche)
Die Quellen von Industrie-/Gewerbelärm weisen sehr unterschiedliche Ausmaße auf. Es kann sich um große Industrie anlagen oder auch kleine konzentrierte Quellen handeln wie kleine Werkzeuge oder Maschinen in einer Fabrik. Deshalb bedarf es eines geeigneten Modellierungsverfahrens für die jeweilige zu bewertende Quelle. Je nach Größe und Verteilung mehrerer Einzelquellen über eine Fläche, die alle zum selben Industriestandort gehören, können diese als Punktquellen, Linienquellen oder Flächenquellen modelliert werden. In der Praxis beruhen die Berechnungen der Schalleinflüsse stets auf Punktquellen, jedoch können mehrere Punktquellen verwendet werden, um eine komplexe Quelle darzustellen, die sich überwiegend über eine Linie oder eine Fläche erstreckt.
Anzahl und Position von Ersatzschallquellen
Die realen Schallquellen werden mittels Ersatzschallquellen modelliert, die durch eine oder mehrere Punktquellen dargestellt werden, so dass die Gesamtschallleistung der realen Quelle der Summe der einzelnen Schallleistungen entspricht, die den verschiedenen Punktquellen zugeordnet werden.
Für die Festlegung der Anzahl zu verwendender Punktquellen gelten folgende allgemeine Regeln:
- Linien- oder Flächenquellen, deren größte Abmessung weniger als die Hälfte des Abstands zwischen der Quelle und dem Empfänger beträgt, können als einzelne Punktquellen modelliert werden.
- Quellen, deren größte Abmessung mehr als die Hälfte des Abstands zwischen der Quelle und dem Empfänger beträgt, sollten als eine Reihe nicht zusammenhängender Punktquellen in einer Linie oder als eine Reihe nicht zusammenhängender Punktquellen über eine Fläche so modelliert werden, dass für jede dieser Quellen die Bedingung des halben Abstands erfüllt ist. Die Verteilung über eine Fläche kann auch die vertikale Verteilung von Punktquellen einschließen.
- Bei Quellen, deren größte Abmessung in der Höhe über 2 m oder nahe dem Boden beträgt, sollte die Höhe der Quelle mit besonderer Sorgfalt behandelt werden. Eine Verdoppelung der Quellenzahl, indem die Quellen lediglich in der z-Komponente verteilt werden, führt nicht unbedingt zu einem wesentlich besseren Ergebnis.
- Für jede Quelle gilt, dass eine Verdoppelung der Quellenzahl im Quellenbereich (in allen Dimensionen) nicht unbedingt zu einem signifikant besseren Ergebnis führt.
Die Position der Ersatzschallquellen lässt sich angesichts der Vielfalt an möglichen Konfigurationen eines Industrie-/Gewerbestandorts nicht festlegen. Hier sind im Regelfall bewährte Praktiken anzuwenden.
Schallleistungspegel
Allgemeines
Die folgenden Angaben bilden das komplette Paket von Eingangsdaten für Berechnungen der Schallausbreitung mit den für die Erstellung von Lärmkarten verwendeten Verfahren:
- Spektrum der abgestrahlten Schallleistungspegel in Oktavbändern,
- Betriebszeiten (Tag, Abend, Nacht, im Jahresdurchschnitt),
- Ort (Koordinaten x, y) und Höhe (z) der Schallquelle,
- Art der Quelle (Punkt, Linie, Fläche),
- Abmessungen und Ausrichtung,
- Betriebsbedingungen der Quelle,
- Richtwirkung der Quelle.
Die Schallleistung von Punkt-, Linien- und Flächenquellen ist wie folgt zu bestimmen:
- für eine Punktquelle die Schallleistung LW und die Richtwirkung als Funktion der drei orthogonalen Koordinaten (x, y, z).
- Es lassen sich zwei Arten von Linienquellen bestimmen:
- Linienquellen, die Förderbänder, Rohrleitungen usw. darstellen, die Schallleistung je Meter Länge LW' und die Richtwirkung als Funktion der beiden zur Achse der Linienquelle orthogonalen Koordinaten;
- Linienquellen, die Fahrzeuge in Bewegung darstellen, werden nach Gleichung (2.2.1) berechnet.
- für eine Flächenquelle die Schallleistung je Quadratmeter LW/m2, und keine Richtwirkung (wirkt horizontal oder vertikal).
Die Betriebszeiten sind ein wesentlicher Eingangswert für die Berechnung von Schallpegeln. Die Betriebszeiten sind für den Tag, den Abend und die Nacht anzugeben; kommen für die Ausbreitung verschiedene meteorologische Kategorien zur Anwendung, die jeweils für die Zeiträume Tag, Nacht und Abend definiert sind, so ist eine detailliertere Verteilung der Betriebszeiten in Teilzeiträumen anzugeben, die der Verteilung der meteorologischen Kategorien entsprechen. Diese Angaben müssen auf einem Jahresdurchschnitt beruhen.
Der Korrekturwert für die Betriebszeiten, der für die Ermittlung der korrigierten Schallleistung zur Quellenschallleistung hinzuzurechnen ist, die für die Berechnungen über den jeweiligen Zeitraum zu verwenden ist, wird als CW in dB wie folgt berechnet:
| CW = 10 x lg(T/Tref) | (2.4.1) |
Hierbei gilt:
T ist die aktive Zeit der Quelle je Zeitraum im Jahresdurchschnitt in Stunden.
Tref ist der Referenzzeitraum in Stunden (z.B. Tag mit 12 Stunden, Abend mit 4 Stunden, Nacht mit 8 Stunden).
Für die dominierenderen Quellen ist der Korrekturwert für die Betriebszeiten im Jahresdurchschnitt mit mindestens einer Toleranz von 0,5 dB anzusetzen, um eine akzeptable Genauigkeit zu erreichen (dies ist gleichbedeutend mit einer Unsicherheit von weniger als 10 % bei der Festlegung der aktiven Zeit der Quelle).
Richtwirkung der Quelle
Die Richtwirkung einer Quelle ist in hohem Maße abhängig von der Position der Ersatzschallquellen in Bezug auf Flächen in der Nähe. Da bei der Ausbreitungsmethode die Reflexion von Flächen in der Nähe ebenso wie deren schalldämpfende Wirkung berücksichtigt werden, ist der Position dieser Flächen besondere Beachtung zu schenken. Üblicherweise werden die beiden folgenden Fälle unterschieden:
- Die Schallleistung und Richtwirkung einer Quelle werden bestimmt und bezogen auf eine bestimmte reale Quelle angegeben, wenn diese sich im freien Schallfeld befindet (ohne Berücksichtigung des Geländeeinflusses). Dies erfolgt gemäß den Festlegungen zur Ausbreitung, wenn angenommen wird, dass keine Fläche in der Nähe weniger als 0,01 m von der Quelle entfernt ist und Flächen in einer Entfernung von 0,01 m oder mehr in die Berechnung der Ausbreitung einbezogen werden.
- Die Schallleistung und Richtwirkung einer Quelle werden bestimmt und relativ zu einer bestimmten realen Quelle angegeben, wenn diese sich an einem bestimmten Ort befindet und deshalb die Schallleistung und Richtwirkung der Quelle tatsächlich "äquivalent" sind, da sie die Modellierung des Einflusses der Flächen in der Nähe einschließt. Dies erfolgt in einem "halbfreien Schallfeld" gemäß der Definition der Schallausbreitung. In diesem Fall sind die modellierten Flächen in der Nähe bei der Berechnung der Ausbreitung nicht zu berücksichtigen.
Die Richtwirkung ist in der Berechnung als ein Faktor ΔLW,dir,xyz (x, y, z) auszudrücken, der zur Schallleistung hinzuzurechnen ist, um die korrekte gerichtete Schallleistung einer Referenzschallquelle bei Schallausbreitung in der angegebenen Richtung zu erhalten.
Der Faktor kann als Funktion des durch (x, y, z) definierten Richtungsvektors mit
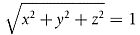 angegeben werden.
Diese Richtwirkung kann auch mittels anderer Koordinatensysteme, wie etwa Winkelkoordinatensysteme, ausgedrückt werden.
angegeben werden.
Diese Richtwirkung kann auch mittels anderer Koordinatensysteme, wie etwa Winkelkoordinatensysteme, ausgedrückt werden.
2.5. Berechnung der Schallausbreitung von Straßen-, Eisenbahn- und Industrie-/Gewerbequellen
2.5.1. Anwendungsbereich und Anwendbarkeit des Verfahrens 21
In diesem Dokument wird ein Verfahren zur Berechnung der Dämpfung von Schall während seiner Ausbreitung im Freien beschrieben. Bei Kenntnis der Quelleigenschaften berechnet dieses Verfahren den äquivalenten Dauerschallpegel am Empfängerpunkt für zwei spezielle Klassen atmosphärischer Bedingungen:
- Ausbreitung unter den Bedingungen der Abwärtsbrechung (positiver vertikaler Gradient der effektiven Schallgeschwindigkeit) von der Quelle zum Empfänger;
- homogene atmosphärische Bedingungen (kein vertikaler Gradient der effektiven Schallgeschwindigkeit) im gesamten Ausbreitungsgebiet.
Das in diesem Dokument beschriebene Berechnungsverfahren gilt für Industrie-/Gewerbe anlagen sowie Verkehrsmittel auf dem Landweg. Es gilt somit insbesondere für Straßen- und Eisenbahnverkehrs anlagen. Der Flugverkehr fällt nur beim Schall, der während Tätigkeiten am Boden entsteht, in den Anwendungsbereich des Verfahrens; Starts und Landungen gehören nicht dazu.
Einrichtungen der industriellen/gewerblichen Infrastruktur, die impulsförmige oder starke tonale Geräusche entsprechend der Beschreibung in ISO 1996-2:2007 emittieren, fallen nicht in den Anwendungsbereich dieses Verfahrens.
Das Berechnungsverfahren liefert keine Ergebnisse für die Bedingungen der Aufwärtsbrechung (negativer vertikaler Gradient der effektiven Schallgeschwindigkeit); eine Näherung dieser Bedingungen kann vielmehr durch homogene Bedingungen bei der Berechnung von Lden gefunden werden.
Zur Berechnung der Dämpfung aufgrund der Absorption in der Atmosphäre im Falle von Transportinfrastruktur werden die Bedingungen von Temperatur und Feuchtigkeit nach ISO 9613-1:1996 berechnet.
Das Verfahren liefert Ergebnisse je Oktavband von 63 Hz bis 8.000 Hz. Diese Berechnungen werden für jede Mittenfrequenz vorgenommen.
Hindernisse mit einer Neigung von mehr als 15° bezogen auf die Vertikale gelten nicht als Reflektoren, sondern werden bei allen anderen Ausbreitungsaspekten wie Bodeneffekten und Beugungen berücksichtigt.
Eine einzelne Abschirmung wird als einzelne Beugung berechnet, zwei oder mehr Abschirmungen in einem einzigen Ausbreitungsweg werden unter Anwendung des nachstehend beschriebenen Verfahrens als aufeinanderfolgende Reihe einzelner Beugungen behandelt.
2.5.2. Verwendete Begriffe
Alle in diesem Dokument verwendeten Abstände, Höhen und Dimensionen werden in Metern (m) angegeben.
Die Bezeichnung MN steht für den Abstand in drei Dimensionen (3D) zwischen den Punkten M und N, der über eine diese Punkte verbindende gerade Linie gemessen wird.
Die Bezeichnung 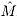 N steht für die Länge des gebogenen Ausbreitungswegs zwischen den Punkten M und N bei günstigen Bedingungen.
N steht für die Länge des gebogenen Ausbreitungswegs zwischen den Punkten M und N bei günstigen Bedingungen.
Reale Höhen werden üblicherweise vertikal im rechten Winkel zur horizontalen Ebene gemessen. Höhen von Punkten über dem lokalen Boden werden mit h bezeichnet, absolute Höhen von Punkten und absolute Höhen des Bodens sind mit dem Buchstaben H zu bezeichnen.
Zur Berücksichtigung des tatsächlichen Reliefs des Geländes entlang eines Ausbreitungswegs wird der Begriff "äquivalente Höhe" eingeführt, der mit dem Buchstaben z bezeichnet wird. Er ersetzt in den Gleichungen zu den Bodeneffekten die realen Höhen.
Die mit dem Großbuchstaben L ohne den Index A bezeichneten Schallpegel werden in Dezibel (dB) je Frequenzband angegeben. Die Schallpegel in Dezibel dB(A) werden mit dem Index A bezeichnet.
Die Summe der Schallpegel aufgrund zueinander inkohärenter Quellen werden mit dem Zeichen 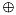 entsprechend der folgenden Definition bezeichnet:
entsprechend der folgenden Definition bezeichnet:
|
| (2.5.1) |
2.5.3. Geometrische Betrachtungen
Quellensegmentierung
Reale Quellen werden durch eine Reihe von Punktquellen oder - im Falle des Eisenbahn- oder des Straßenverkehrs - durch inkohärente Linienquellen beschrieben. Das Ausbreitungsverfahren beruht auf der Annahme, dass Linien- oder Flächenquellen zuvor aufgeteilt wurden, damit sie mittels einer Reihe äquivalenter Punktquellen dargestellt werden können. Dies kann als Vorverarbeitung der Quellendaten erfolgt sein oder im Rahmen der Pathfinder-Komponente der Berechnungssoftware erfolgen. Die Mittel, mit denen dies erfolgt ist, gehören nicht zum Anwendungsbereich der aktuellen Methodik.
Ausbreitungswege
Das Verfahren arbeitet mit einem geometrischen Modell, das aus einer Reihe zusammenhängender Boden- und Hindernisflächen besteht. In Bezug auf die horizontale Ebene wird ein vertikaler Ausbreitungsweg auf einer oder mehreren vertikalen Ebenen aufgetragen. Schließt ein Ausbreitungsweg eine Reflexion an einer vertikalen Fläche ein, die nicht rechtwinklig zur Einfallsebene steht, so verläuft der reflektierte Teil des Ausbreitungswegs in einer weiteren vertikalen Ebene. Werden mehrere vertikale Ebenen verwendet, um den gesamten Ausbreitungsweg von der Quelle bis zum Empfänger zu beschreiben, werden die vertikalen Ebenen sodann aufgefächert (wie beim Auffalten einer Spanischen Wand).
Maßgebliche Höhen über dem Gelände
Die äquivalenten Höhen werden mit Hilfe der mittleren Bezugsebene zwischen der Quelle und dem Empfänger bestimmt. Diese ersetzt das tatsächliche Gelände durch eine fiktive Ebene, die das mittlere Profil des Geländes abbildet.
Abbildung 2.5.a Äquivalente Höhe in Bezug auf den Boden
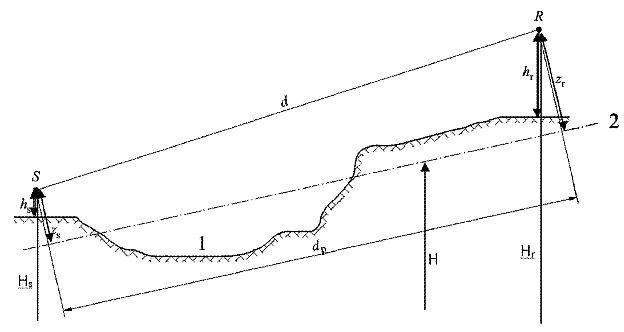
1: Tatsächliches Relief
2: Mittlere Ebene
Die äquivalente Höhe eines Punktes ist seine Höhe im rechten Winkel zur mittleren Grundebene. Die äquivalente Quellenhöhe zs und die äquivalente Empfängerhöhe zr können somit bestimmt werden. Der Abstand zwischen der Quelle und dem Empfänger in der Projektion auf die mittlere Bezugsebene wird durch dp bezeichnet.
Weist die äquivalente Höhe eines Punktes einen negativen Wert auf, d. h. befindet sich der Punkt unterhalb der mittleren Grundebene, wird die Höhe null beibehalten; der äquivalente Punkt ist dann mit seinem möglichen Spiegelbild identisch.
Berechnung der mittleren Ebene
In der Ebene des Ausbreitungsweges kann die Topographie (einschließlich Gelände, Hügel, Dämme und andere von Menschen errichtete Hindernisse, Gebäude usw.) als eine geordnete Menge einzelner Punkte (xk, Hk); k 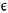 {1, ..., n} beschrieben werden.
Die Punktmenge definiert eine Polylinie oder - äquivalent dazu - eine Abfolge gerader Segmente Hk = akx + bk, x
{1, ..., n} beschrieben werden.
Die Punktmenge definiert eine Polylinie oder - äquivalent dazu - eine Abfolge gerader Segmente Hk = akx + bk, x 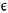 [xk, xk + 1]; k
[xk, xk + 1]; k 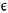 {1,... n}, worin:
{1,... n}, worin:
|
| (2.5.2) |
Die mittlere Ebene wird durch die Gerade Z = ax + b; x 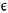 [x1, xn] dargestellt, die an die Polylinie mittels Approximation nach der Methode der kleinsten Quadrate angepasst wird.
Die Gleichung der Mittellinie kann analytisch abgeleitet werden.
[x1, xn] dargestellt, die an die Polylinie mittels Approximation nach der Methode der kleinsten Quadrate angepasst wird.
Die Gleichung der Mittellinie kann analytisch abgeleitet werden.
Verwendet wird:
|
| (2.5.3) |
Die Koeffizienten der Geraden sind wie folgt gegeben:
|
| (2.5.4), |
wobei Segmente mit xk + 1 = xk außer Acht zu lassen sind, wenn die Gleichung 2.5.3 evaluiert wird.
Reflexionen durch Gebäudefassaden und andere vertikale Hindernisse
Reflexionsanteile sind durch die Einführung von Spiegelquellen wie nachfolgend beschrieben zu berücksichtigen.
2.5.4. Modell der Schallausbreitung
Für einen Empfänger R werden die Berechnungen unter Einhaltung folgender Schritte vorgenommen:
- zu jedem Ausbreitungsweg:
- Berechnung der Dämpfung bei günstigen Bedingungen;
- Berechnung der Dämpfung bei homogenen Bedingungen;
- Berechnung des Dauerschallpegels für jeden Ausbreitungsweg;
- Aufsummierung der Dauerschallpegel für alle Ausbreitungswege, die einen bestimmten Empfänger betreffen, wodurch der Gesamtschallpegel am Empfängerpunkt berechnet werden kann.
Zu beachten ist, dass von den Witterungsbedingungen nur die Dämpfungen aufgrund des Bodeneffekts (Aground) und der Beugung (Adif) beeinflusst werden.
2.5.5. Ablauf der Berechnung 21
Für eine Punktquelle S der gerichteten Schallleistung Lw,0,dir und für ein bestimmtes Frequenzband wird der äquivalente Dauerschalldruckpegel am Empfängerpunkt R unter bestimmten Witterungsbedingungen mittels der nachfolgenden Gleichungen bestimmt.
Schallpegel bei günstigen Bedingungen (LF) für einen Ausbreitungsweg (S, R)
| LF = LW,0,dir - AF | (2.5.5) |
Der Term AF repräsentiert die Gesamtdämpfung entlang des Ausbreitungsweges bei günstigen Bedingungen und wird wie folgt aufgeschlüsselt:
| AF =Adiv + Aatm + Aboundary,F | (2.5.6) |
Hierbei gilt:
Adiv ist die geometrische Ausbreitungsdämpfung;
Aatm ist die Dämpfung aufgrund von Luftabsorption;
Aboundary,F ist die Dämpfung aufgrund der Begrenzung des Ausbreitungsmediums bei günstigen Bedingungen. Sie kann folgende Terme beinhalten:
Aground,F für die Dämpfung aufgrund des Bodens bei günstigen Bedingungen;
Adif,F für die Dämpfung aufgrund von Beugung bei günstigen Bedingungen.
Für einen gegebenen Ausbreitungsweg und ein gegebenes Frequenzband sind die folgenden beiden Szenarien möglich:
- entweder Aground,F wird ohne Beugung (Adif,F = 0 dB) und Aboundary,F = Aground,F berechnet;
- oder es wird Adif,F berechnet. Der Bodeneffekt wird in der Adif,F-Gleichung selbst berücksichtigt (Aground, F = 0 dB). Somit ergibt sich Aboundary,F = Adif,F.
Schallpegel bei homogenen Bedingungen (LH) für einen Ausbreitungsweg (S, R)
Das Verfahren ist völlig identisch mit dem Fall der günstigen Bedingungen im vorhergehenden Abschnitt.
| LH = LW,0,dir - AH | (2.5.7) |
Der Term AH repräsentiert die Gesamtdämpfung entlang dem Ausbreitungsweg bei homogenen Bedingungen und wird wie folgt aufgeschlüsselt:
| AH = Adiv + Aatm + Aboundary,H | (2.5.8) |
Hierbei gilt:
Adiv ist die geometrische Ausbreitungsdämpfung;
Aatm ist die Dämpfung aufgrund von Luftabsorption;
Aboundary,H ist die Dämpfung aufgrund der Begrenzung des Ausbreitungsmediums bei homogenen Bedingungen. Sie kann folgende Terme beinhalten:
Aground,H für die Dämpfung aufgrund des Geländes bei homogenen Bedingungen;
Adif,H für die Dämpfung aufgrund von Beugung bei homogenen Bedingungen.
Für einen gegebenen Ausbreitungsweg und ein gegebenes Frequenzband sind die folgenden beiden Szenarien möglich:
- entweder Aground,H (Adif,H = 0 dB) wird ohne Beugung und Aboundary,H = Aground,H berechnet;
- oder es wird Adif,H (Aground,H = 0 dB) berechnet. Der Bodeneffekt wird in der Adif,H-Gleichung berücksichtigt. Somit ergibt sich Aboundary,H = Adif,H
Statistischer Ansatz in städtischen Gebieten für einen Ausbreitungsweg (S, R)
In städtischen Gebieten ist auch ein statistischer Ansatz für die Berechnung der Schallausbreitung hinter die erste Gebäudelinie zulässig, sofern ein solches Verfahren ordnungsgemäß dokumentiert wird, was auch relevante Angaben zur Qualität des Verfahrens einschließt. Dieses Verfahren kann an die Stelle der Berechnung von Aboundary,H und Aboundary,F durch Approximation der Gesamtdämpfung für den direkten Ausbreitungsweg und alle Reflexionen treten. Die Berechnung beruht dann auf der durchschnittlichen Bebauungsdichte und der durchschnittlichen Höhe aller Gebäude in dem Gebiet.
Dauerschallpegel für einen Ausbreitungsweg (S, R)
Der Dauerschallpegel entlang eines Ausbreitungsweges, der von einem bestimmten Punkt ausgeht, wird aus der logarithmischen Summe der bewerteten Schallenergie bei homogenen Bedingungen und der Schallenergie bei günstigen Bedingungen gebildet.
Diese Schallpegel werden durch das mittlere Auftreten p günstiger Bedingungen in Richtung des Ausbreitungsweges (S, R) gewichtet:
|
| (2.5.9) |
Anmerkung: Die Häufigkeitswerte für p werden als Prozentsatz angegeben. Wenn also etwa der Häufigkeitswert 82 % beträgt, würde in der Gleichung (2.5.9) p = 0,82 stehen.
Dauerschallpegel am Punkt R für alle Ausbreitungswege
Der Gesamt-Langzeit-Dauerschallpegel am Empfänger für ein Frequenzband wird durch die energetische Summierung der Beiträge aller N Ausbreitungswege für alle Arten errechnet:
|
| (2.5.10) |
Hierbei gilt:
n ist der Index der Ausbreitungswege zwischen S und R.
Die Berücksichtigung von Reflexionen mittels Spiegelquellen wird näher beschrieben. Der Prozentsatz der Häufigkeit günstiger Bedingungen im Falle der Reflexion eines Ausbreitungsweges an einem vertikalen Hindernis ist als identisch mit der Häufigkeit des direkten Ausbreitungsweges anzusetzen.
Wenn S' die Spiegelquelle von S, ist, dann wird das Auftreten p' des Ausbreitungsweges (S',R) als gleich dem Auftreten p des Ausbreitungsweges (Si,R) angesetzt.
Dauerschallpegel am Punkt R in Dezibel A (dBA)
Der Gesamtschallpegel in Dezibel A (dBA) wird durch Summierung der Pegel in jedem einzelnen Frequenzband bestimmt:
|
| (2.5.11) |
Dabei ist i der Index des Frequenzbands. AWC ist die A-Bewertungskorrektur wie folgt:
| Frequenz [Hz] | 63 | 125 | 250 | 500 | 1.000 | 2.000 | 4.000 | 8.000 |
| AWCf,i [dB] | -26,2 | -16,1 | -8,6 | -3,2 | 0 | 1,2 | 1,0 | -1,1 |
Dieser Pegel LAeq,LT stellt das Endresultat dar, d. h. dem A-bewerteten Langzeit-Dauerschallpegel am Empfängerpunkt in einem bestimmten Referenzzeitraum (z.B. Tag oder Abend oder Nacht oder einer kürzeren Zeit am Tag, am Abend oder in der Nacht).
2.5.6. Berechnung der Schallausbreitung bei Straßen-, Eisenbahn- und Industrie-/Gewerbequellen 21
Geometrische Zerstreuung
Die geometrische Ausbreitungsdämpfung Adiv entspricht einer Verringerung des Schallpegels mit zunehmender Ausbreitungsentfernung. Für eine Punktschallquelle im freien Schallfeld wird die Dämpfung in dB angegeben durch:
| Adiv = 20 x lg(d) + 11 | (2.5.12) |
wobei d die direkte 3D-Schrägentfernung zwischen der Quelle und dem Empfänger ist.
Luftabsorption
Die Dämpfung aufgrund von Luftabsorption Aatm während der Ausbreitung über eine Entfernung d wird in dB durch folgende Gleichung angegeben:
| Aatm = αatm · d/1.000 | (2.5.13) |
Hierbei gilt:
d ist die direkte 3D-Schrägentfernung zwischen der Quelle und dem Empfänger in m;
αatm ist der Koeffizient der Dämpfung in der Atmosphäre in dB/km in der nominellen Mittenfrequenz für jedes Frequenzband gemäß ISO 9613-1.
Die Werte des Koeffizienten αatm werden für eine Temperatur von 15 °C, eine relative Feuchtigkeit von 70 % und einen Luftdruck von 101.325 Pa angegeben. Sie werden mit den genauen Mittenfrequenzen des Frequenzbandes berechnet. Diese Werte erfüllen die Norm ISO 9613-1. Liegen meteorologische Daten vor, so ist der meteorologische Langzeitdurchschnitt zu verwenden.
Bodeneffekt
Die Dämpfung aufgrund des Bodeneffekts ist vor allem das Ergebnis der Interferenz zwischen dem reflektierten Schall und dem Schall, der sich direkt von der Quelle zum Empfänger ausbreitet. Sie ist physisch mit der akustischen Absorption des Geländes verbunden, über dem sich der Schall ausbreitet. Sie ist aber auch erheblich von den atmosphärischen Bedingungen während der Ausbreitung abhängig, da sich durch die Schallstrahlkrümmung die Höhe des Ausbreitungsweges über dem Boden ändert und so die Einflüsse des Bodens und des Geländes nahe der Quelle an Bedeutung gewinnen oder verlieren.
Wenn die Ausbreitung zwischen der Quelle und dem Empfänger durch ein Hindernis in der Ausbreitungsebene beeinflusst wird, wird der Bodeneffekt für die Quellen- und die Empfängerseite getrennt berechnet. Dabei beziehen sich zs und zr auf die äquivalente Quellen- und/oder Empfängerposition, wie im Weiteren im Zusammenhang mit der Berechnung der Beugung Adif dargestellt wird.
Akustische Charakterisierung des Bodens
Die akustischen Absorptionseigenschaften des Bodens stehen vor allem mit seiner Porosität in Verbindung. Ein dichter Boden ist im Allgemeinen reflektierend, ein poröser Boden absorbierend.
Für die Zwecke einer operativen Berechnung wird die akustische Absorption eines Bodens durch einen dimensionslosen Koeffizienten G zwischen 0 und 1 dargestellt. G ist unabhängig von der Frequenz. Tabelle 2.5.a enthält die G-Werte für den Boden im Freien. Der durchschnittliche Wert des Koeffizienten G über einen Ausbreitungsweg liegt in der Regel im Bereich von 0 bis 1.
Tabelle 2.5.a G-Werte für verschiedene Bodenarten
| Beschreibung | Art | (kPa·s/m2) | G-Wert |
| Sehr weich (wie Schnee oder Moos) | A | 12,5 | 1 |
| Weicher Waldboden (kurzes, dichtes heideartiges oder dickes Moos) | B | 31,5 | 1 |
| Nicht verdichteter loser Boden (Rasen, Gras, loser Boden) | C | 80 | 1 |
| Normaler nicht verdichteter Boden (Wald boden, Weideland) | D | 200 | 1 |
| Verdichtetes Feld und Schotter (verdichteter Rasen, Parkgebiete) | E | 500 | 0,7 |
| Verdichteter dichter Boden (Schotterstraße, Parkplatz) | F | 2.000 | 0,3 |
| Harte Oberflächen (zumeist normaler Asphalt, Beton) | G | 20.000 | 0 |
| Sehr harte und dichte Oberflächen (dichter Asphalt, Beton, Wasser) | H | 200.000 | 0 |
Gpath wird definiert als der Anteil an absorbierendem Boden über den gesamten betrachteten Ausbreitungsweg.
Wenn die Quelle und der Empfänger nahe beieinander liegen, so dass dp ≤ 30(zs + zr), ist der Unterschied zwischen der Bodenart nahe der Quelle und der Bodenart nahe dem Empfänger unerheblich. Um dem Rechnung zu tragen, wird der Bodenfaktor Gpath letztlich wie folgt korrigiert:
|
| (2.5.14) |
wobei Gs der Bodenfaktor im Bereich der Quelle ist. Gs = 0 für Straßenfahrbahnen 1, feste Fahrbahnen. Gs=1 für Bahngleise auf Schotterbettung. Im Falle von industriellen/gewerblichen Quellen und Anlagen gibt es keine pauschale Antwort.
G kann mit dem Strömungswiderstand in Verbindung gebracht werden.
Abbildung 2.5.b Bestimmung des Bodenkoeffizienten Gpath über einen Ausbreitungsweg
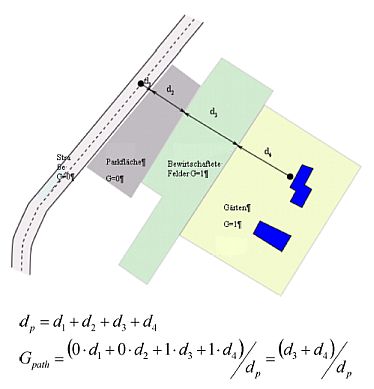
Die Abstände dn werden durch eine zweidimensionale Projektion auf die horizontale Ebene bestimmt.
In den folgenden zwei Unterabschnitten über die Berechnung bei homogenen bzw. günstigen Bedingungen kommen erstmals die generischen Bezeichnungen Gw und  m für die Absorption des Bodens zur Anwendung.
Tabelle 2.5.b zeigt die Entsprechung zwischen diesen Bezeichnungen und den Variablen Gpath und G'path.
m für die Absorption des Bodens zur Anwendung.
Tabelle 2.5.b zeigt die Entsprechung zwischen diesen Bezeichnungen und den Variablen Gpath und G'path.
Tabelle 2.5.b Übereinstimmungen zwischen  w und
w und  m und (Gpath, G'path)
m und (Gpath, G'path)
| Homogene Bedingungen | Günstige Bedingungen | |||||
| Aground | Δground(S,O) | Δground(O,R) | Aground | Δground(S,O) | Δground(O,R) | |
 w w | G'path | Gpath | ||||
 m m | G'path | Gpath | G'path | Gpath | ||
| 1) Die Absorption poröser Straßenbeläge wird im Emissionsmodell berücksichtigt. | ||||||
Berechnungen bei homogenen Bedingungen
Die Dämpfung aufgrund des Bodeneffekts bei homogenen Bedingungen wird nach den folgenden Gleichungen berechnet:
wenn Gpath ≠ 0
|
| (2.5.15) |
Hierbei gilt:
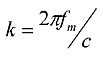
ƒm ist die nominelle Mittenfrequenz des betrachteten Frequenzbands in Hz, c ist die Geschwindigkeit des Schalls in der Luft (als 340 m/s angenommen), und Cƒ wird definiert durch:
|
| (2.5.16), |
wobei die Werte von w durch die nachstehende Gleichung gegeben sind:
|
| (2.5.17). |
 w kann gleich Gpath oder G'path sein, je nachdem, ob der Bodeneffekt mit oder ohne Beugung berechnet wird und welcher Art der Boden unter der Quelle ist (reale Quelle oder gebeugt). Dies wird in den folgenden Unterabschnitten näher erläutert und in der Tabelle 2.5.b zusammengefasst.
w kann gleich Gpath oder G'path sein, je nachdem, ob der Bodeneffekt mit oder ohne Beugung berechnet wird und welcher Art der Boden unter der Quelle ist (reale Quelle oder gebeugt). Dies wird in den folgenden Unterabschnitten näher erläutert und in der Tabelle 2.5.b zusammengefasst.
|
|
ist der untere Grenzwert von Aground,H.
Für einen Ausbreitungsweg (Si, R) bei homogenen Bedingungen ohne Beugung:
 w = G'path
w = G'path
 m = G'path
m = G'path
Zum Ausbreitungsweg mit Beugung siehe den Abschnitt "Beugung" mit den Definitionen von  w und
w und  m.
m.
wenn Gpath = 0: Aground,H = -3 dB
Der Term - 3(1 -  m) trägt dem Umstand Rechnung, dass, wenn die Quelle und der Empfänger weit auseinander liegen, die erste quellenseitige Reflexion nicht mehr auf der quellnahen Oberfläche, sondern auf natürlichem Gelände erfolgt.
m) trägt dem Umstand Rechnung, dass, wenn die Quelle und der Empfänger weit auseinander liegen, die erste quellenseitige Reflexion nicht mehr auf der quellnahen Oberfläche, sondern auf natürlichem Gelände erfolgt.
Berechnung bei günstigen Bedingungen
Der Bodeneffekt bei günstigen Bedingungen wird mit der Gleichung für Aground,H berechnet, allerdings mit folgenden Änderungen:
Wenn Gpath ≠ 0
- In Gleichung (2.5.15) (Aground,H) werden die Höhen zs und zr ersetzt durch zs +δ zs +δ zT bzw. zr +δ zr +δ zT wobei
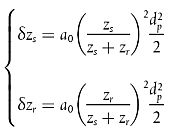
(2.5.19) ao = 2 x 10-4 m-1 die Umkehrung des Bogenhalbmessers ist
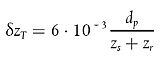
- Der untere Grenzwert von Aground,F (berechnet mit unveränderten Höhen) ist abhängig von der Geometrie des Ausbreitungsweges:
|
| (2.5.20) |
Wenn Gpath = 0
Aground,F, = Aground,F,min
Die Höhenkorrekturen δ zs und δ zr berücksichtigen die Wirkung der Schallstrahlkrümmung. δ zT trägt der Wirkung der Turbulenz Rechnung.
 m kann also gleich Gpath oder G'path sein, je nachdem, ob der Bodeneffekt mit oder ohne Beugung berechnet wird und welcher Art der Boden unter der Quelle ist (reale Quelle oder gebeugt). Dies wird in den folgenden Unterabschnitten näher erläutert.
m kann also gleich Gpath oder G'path sein, je nachdem, ob der Bodeneffekt mit oder ohne Beugung berechnet wird und welcher Art der Boden unter der Quelle ist (reale Quelle oder gebeugt). Dies wird in den folgenden Unterabschnitten näher erläutert.
Für einen Ausbreitungsweg (Si,R) bei günstigen Bedingungen ohne Beugung:
 w = Gpath in Gleichung (2.5.17);
w = Gpath in Gleichung (2.5.17);
 m = G'path.
m = G'path.
Zum Ausbreitungsweg mit Beugung siehe den nächsten Abschnitt mit den Definitionen von Gw und  m.
m.
Beugung
Generell ist die Beugung an der Oberkante jedes Hindernisses zu untersuchen, das sich im Ausbreitungsweg befindet. Verläuft der Ausbreitungsweg ,hoch genug' über der Beugungskante, so kann Adif = 0 gesetzt und eine direkte Sicht berechnet werden, konkret durch die Bestimmung von Aground.
In der Praxis werden die folgenden Spezifikationen in der einzigen vertikalen Ebene berücksichtigt, die sowohl die Quelle als auch den Empfänger umfasst (eine aufgefaltete spanische Wand bei einem Ausbreitungsweg einschließlich Reflexionen). Der Direktstrahl von der Quelle zum Empfänger ist eine gerade Linie bei homogenen Ausbreitungsbedingungen und eine gekrümmte Linie (ein Bogen mit einem Radius, der von der Länge des geraden Strahls abhängt) bei günstigen Ausbreitungsbedingungen.
Wird der Direktstrahl nicht blockiert, dann wird Kante D angestrebt, die die größte Weglängendifferenz δ ergibt (der kleinste absolute Wert, da diese Weglängendifferenzen negativ sind). Die Beugung wird berücksichtigt, wenn
- diese Weglängendifferenz größer ist als -λ/20 und
- das "Rayleigh-Kriterium" erfüllt ist.
Dies ist der Fall, wenn δ größer ist alsλ/4 -δ*, wobei δ* die mit derselben Kante D berechnete Weglängendifferenz ist, jedoch bezogen auf die Spiegelquelle S*, welche mithilfe der quellenseitigen mittleren Bezugsebene berechnet wird, und bezogen auf den Spiegelempfänger R*, welcher mithilfe der empfängerseitigen mittleren Bezugsebene berechnet wird. Für die Berechnung von δ* werden nur die Punkte S*,D und R* berücksichtigt - andere Kanten, die den Weg von S* -> D -> R* blockieren, werden vernachlässigt.
Im Hinblick auf die vorstehenden Ausführungen wird die Wellenlänge λ unter Verwendung der nominellen Mittenfrequenz und einer Schallgeschwindigkeit von 340 m/s berechnet.
Sind diese beiden Bedingungen erfüllt, werden Quellenseite und Empfängerseite durch die Kante D getrennt, es werden zwei getrennte mittlere Bezugsebenen berechnet, und Adif wird wie im restlichen Teil dieses Abschnitts beschrieben berechnet. Andernfalls wird für diesen Ausbreitungsweg keine Dämpfung durch Beugung berücksichtigt, es wird eine gemeinsame mittlere Bezugsebene für den Weg von S -> R berechnet, und Aground wird ohne Beugung berechnet ( Adif = 0 dB). Diese Regel gilt sowohl bei homogenen als auch bei günstigen Bedingungen.
Wenn für ein bestimmtes Frequenzband eine Berechnung nach dem in diesem Abschnitt beschriebenen Verfahren vorgenommen wird, wird im Falle der Berechnung der Gesamtdämpfung Aground mit 0 dB angesetzt. Der Bodeneffekt ist direkt in der allgemeinen Gleichung zur Beugungsberechnung berücksichtigt.
Die hier vorgeschlagenen Gleichungen werden verwendet, um die Beugung an dünnen und dicken Schallschirmen, Gebäuden, (natürlichen und künstlichen) Wällen und durch die Kanten von Böschungen, Geländeeinschnitten und Viadukten zu berechnen.
Werden in einem Ausbreitungsweg mehrere Beugungshindernisse festgestellt, werden sie als Mehrfachbeugung behandelt, indem das im folgenden Abschnitt zur Berechnung der Weglängendifferenz beschriebene Verfahren angewendet wird.
Die hier dargelegten Verfahren werden verwendet, um die Dämpfungen sowohl bei homogenen als auch bei günstigen Bedingungen zu berechnen. Die Schallstrahlkrümmung wird bei der Berechnung der Weglängendifferenz sowie zur Berechnung der Bodeneffekte vor und nach der Beugung berücksichtigt.
Allgemeine Grundsätze
Abbildung 2.5.c veranschaulicht das allgemeine Verfahren der Berechnung der Dämpfung aufgrund von Beugung. Dieses Verfahren basiert auf der Untergliederung des Ausbreitungswegs in zwei Teile: den "quellenseitigen" Ausbreitungsweg zwischen der Quelle und dem Beugungspunkt und den "empfängerseitigen" Ausbreitungsweg zwischen dem Beugungspunkt und dem Empfänger.
Folgendes wird berechnet:
- ein Bodeneffekt, quellenseitig, Δground(S,O),
- ein Bodeneffekt, empfängerseitig, Δground(O,R)
- und drei Beugungen:
- zwischen der Quelle S und dem Empfänger R: Δdif(S,R),
- zwischen der Spiegelquelle S' und R: Δdif(S',R),
- zwischen S und dem Spiegelempfänger R': Δdif(S,R').
Abbildung 2.5.c Geometrie einer Berechnung der Dämpfung aufgrund von Beugung
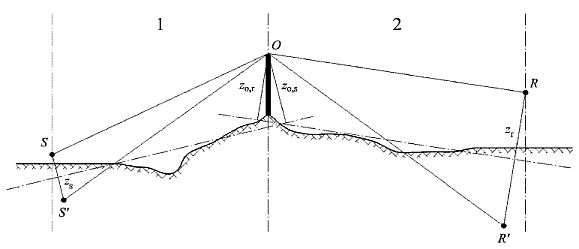
1: Quellenseite.
2: Empfängerseite.
Hierbei gilt:
S ist die Quelle;
R ist der Empfänger;
S' ist die Spiegelquelle bezogen auf die quellseitige mittlere Bezugsebene;
R' ist der Spiegelempfänger bezogen auf die empfängerseitige mittlere Bezugsebene;
O ist der Beugungspunkt;
zs ist die äquivalente Höhe der Quelle S bezogen auf die quellenseitige mittlere Bezugsebene;
zo,s ist die äquivalente Höhe des Beugungspunkts O bezogen auf die quellenseitige mittlere Bezugsebene;
zr ist die äquivalente Höhe des Empfängers R bezogen auf die empfängerseitige mittlere Bezugsebene;
zo,r ist die äquivalente Höhe des Beugungspunkts O bezogen auf die empfängerseitige mittlere Bezugsebene.
Die Unregelmäßigkeit des Bodens zwischen der Quelle und dem Beugungspunkt sowie zwischen dem Beugungspunkt und dem Empfänger wird mittels äquivalenter Höhen berücksichtigt, die in Bezug auf die mittlere Grundebene, zuerst quellenseitig und dann empfängerseitig (zwei mittlere Grundebenen), anhand des im Unterabschnitt zu erheblichen Höhen über dem Boden beschriebenen Verfahrens berechnet werden.
Reine Beugung
Für die reine Beugung ohne Bodeneffekte wird die Dämpfung angegeben durch:
|
| (2.5.21) |
Hierbei gilt:
| Ch = 1 | (2.5.22) |
λ ist die Wellenlänge der nominalen Mittenfrequenz des betrachteten Frequenzbandes;
δ ist die Weglängendifferenz zwischen dem gebeugten Ausbreitungsweg und dem direkten Ausbreitungsweg (siehe nächsten Unterabschnitt "Berechnung der Weglängendifferenz");
C" ist ein Koeffizient, der zur Berücksichtigung von Mehrfachbeugungen eingesetzt wird:
C" = 1 für eine Einzelbeugung.
Wenn im Falle der Mehrfachbeugung e die Gesamtlänge des Ausbreitungswegs zwischen dem ersten und dem letzten Beugungspunkt (Verwendung gebogener Strahlen bei günstigen Bedingungen) und e größer als 0,3 m ist (andernfalls C" = 1), dann wird dieser Koeffizient bestimmt durch:
|
| (2.5.23) |
Die Werte von Δdif sind zu begrenzen:
- wenn Δdif < 0: Δdif = 0 dB,
- wenn Δdif > 25: Δdif = 25 dB für eine Beugung an einer horizontalen Kante und nur beim Term Δdif, der in der Berechnung von Adif eine Rolle spielt. Diese Obergrenze gilt nicht bei den Δdif Termen, die in die Berechnung von Δground eingreifen, oder für eine Beugung an einer vertikalen Kante (seitliche Beugung) im Falle der Erstellung von Lärmkarten für Industrie-/Gewerbelärm.
Berechnung der Weglängendifferenz
Die Weglängendifferenz δ wird auf einer vertikalen Ebene berechnet, die die Quelle und den Empfänger umfasst. Dies ist eine Approximation im Verhältnis zum Fermatschen Prinzip. Die Approximation bleibt hier gültig (Linienquellen). Die Weglängendifferenz δ wird wie in den nachstehenden Abbildungen ausgehend von den vorgefundenen Situationen berechnet.
Homogene Bedingungen
Abbildung 2.5.d Berechnung der Weglängendifferenz unter homogenen Bedingungen. O, O1 und O2 sind die Beugungspunkte
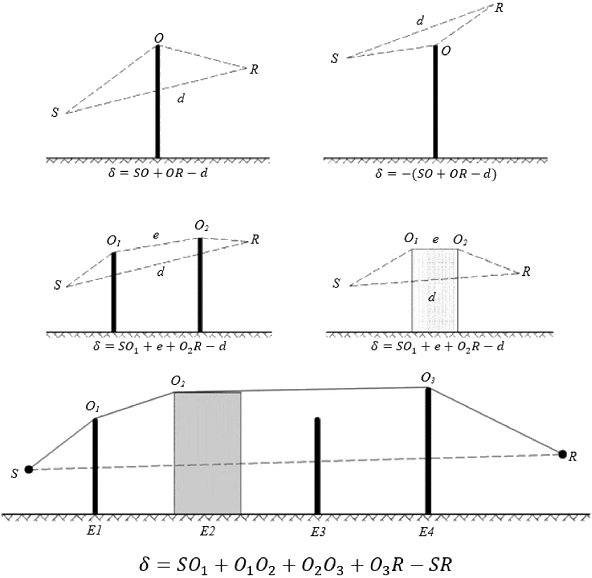
Hinweis: Für jede Konfiguration wird der Ausdruck δ angegeben.
Günstige Bedingungen
Abbildung 2.5.e Berechnung der Weglängendifferenz bei günstigen Bedingungen (Einzelbeugung)
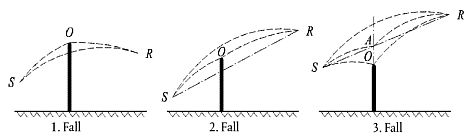
Bei günstigen Bedingungen haben die drei gebogenen Schallstrahlen 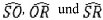 einen identischen Kurvenradius Γ, der definiert wird durch:
einen identischen Kurvenradius Γ, der definiert wird durch:
| Γ = max(1.000,8d) | (2.5.24) |
Dabei ist d der direkte 3D-Abstand zwischen Quelle und Empfänger des aufgefalteten Weges.
Die Länge eines Schallstrahlbogens MN wird bei günstigen Bedingungen mit 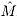 N bezeichnet.
Diese Länge ist gleich:
N bezeichnet.
Diese Länge ist gleich:
|
| (2.5.25) |
Im Prinzip sollten bei der Berechnung der Weglängendifferenz bei günstigen Bedingungen δF (siehe Abbildung 2.5.e) drei Szenarien betrachtet werden. In der Praxis genügen zwei Gleichungen:
- wenn der direkte Schallstrahl SR durch das Hindernis verdeckt wird (1. und 2. Fall in Abbildung 2.5.e):
|
| (2.5.26), |
- wenn der direkte Schallstrahl SR nicht durch das Hindernis verdeckt wird (3. Fall in Abbildung 2.5.e):
|
| (2.5.27), |
wobei A der Schnittpunkt des direkten Schallstrahls SR und der Verlängerung des Beugungshindernisses ist.
Für die Mehrfachbeugungen bei günstigen Bedingungen:
- Bestimmen der konvexen Hülle, die durch die verschiedenen potenziellen Beugungskanten definiert wird;
- Ausschließen der Beugungskanten, die nicht an der Grenze der konvexen Hülle liegen;
- Berechnen von δF ausgehend von den Längen des gebogenen Schallstrahls durch Aufgliederung des gebeugten Ausbreitungsweges in so viele Bogensegmente wie nötig (siehe Abbildung 2.5.f)
|
| (2.5.28) |
Bei günstigen Bedingungen besteht der Ausbreitungsweg in der vertikalen Ausbreitungsebene stets aus Segmenten in Form eines Kreises, dessen Radius durch den 3D-Abstand zwischen Quelle und Empfänger gegeben ist, d. h., alle Segmente eines Ausbreitungswegs weisen denselben Kurvenradius auf. Ist der direkte Bogen zwischen Quelle und Empfänger blockiert, bestimmt sich der Ausbreitungsweg als die kürzeste konvexe Kombination von Bogen, die alle Hindernisse umhüllen. Konvex bedeutet in diesem Zusammenhang, dass an jedem Beugungspunkt das abgehende Strahlsegment gegenüber dem eingehenden Strahlsegment nach unten abgelenkt wird.
Abbildung 2.5.f Beispiel einer Berechnug der Weglängendifferenz bei günstigen Bedingungen im Falle von Mehrfachbeugungen
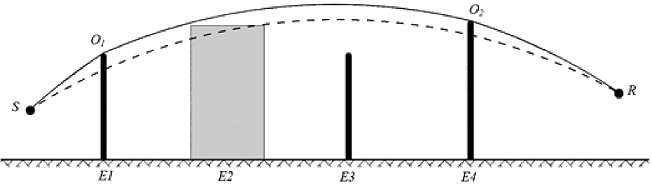
In dem in Abbildung 2.5.f dargestellten Szenario ist die Weglängendifferenz:
|
| (2.5.29) |
Berechnung der Dämpfung Adif
Die Dämpfung aufgrund von Beugung unter Berücksichtigung der quellen- und empfängerseitigen Bodeneffekte wird nach den folgenden allgemeinen Gleichungen berechnet:
| Adif = Δdif(S,R) + Δground(S,O) + Δground(On ,R) | (2.5.30) |
Hierbei gilt:
- Δdif(S,R) ist die Dämpfung aufgrund der Beugung zwischen der Quelle S und dem Empfänger R;
- Δground(S,O) ist die Dämpfung aufgrund des Bodeneffekts auf der Quellenseite, bewertet mittels der Beugung auf der Quellenseite; wobei als vereinbart gilt, dass O = O1 im Falle von Mehrfachbeugungen wie in Abbildung 2.5.f
- Δground(O,R) ist die Dämpfung aufgrund des Bodeneffekts auf der Empfängerseite, gewichtet nach der
Beugung auf der Empfängerseite (siehe den folgenden Unterabschnitt "Berechnung des Terms Δground(O,R)").
Berechnung des Terms Δground(S,O)
|
|
Dabei gilt:
- Aground(S,O) ist die Dämpfung aufgrund des Bodeneffekts zwischen der Quelle S und dem Beugungspunkt O. Dieser Term wird gemäß den vorherigen Unterabschnitten 'Berechnung bei homogenen Bedingungen' und 'Berechnung bei günstigen Bedingungen' berechnet, und zwar ausgehend von folgenden Hypothesen:
- zr = zo,s,
- Gpath wird zwischen O und R berechnet.
Bei homogenen Bedingungen  w= Gparth in Gleichung (2.5.17) und
w= Gparth in Gleichung (2.5.17) und  m= Gparth in Gleichung (2.5.18).
m= Gparth in Gleichung (2.5.18).
Bei günstigen Bedingungen  w= Gparth in Gleichung (2.5.17) und
w= Gparth in Gleichung (2.5.17) und  m= Gparth in Gleichung (2.5.20).
m= Gparth in Gleichung (2.5.20).
- Δdif(S,R') ist die Dämpfung aufgrund der Beugung zwischen S und dem Spiegelempfänger R', berechnet wie im vorherigen Abschnitt 'Reine Beugung'.
- Δdif(S,R) ist die Dämpfung aufgrund der Beugung zwischen S und R, berechnet wie im vorherigen Unterabschnitt 'Reine Beugung'.
Im Sonderfall, wenn die Quelle unter der mittleren Bezugsebene liegt: Δdif(S,R) = Δdif(S',R) und Δground(S,O) = Aground(S,O)
Berechnung des Terms Δground(O,R)
|
|
Dabei gilt:
- Aground(O,R) ist die Dämpfung aufgrund des Bodeneffekts zwischen dem Beugungspunkt O und dem Empfänger R. Dieser Term wird gemäß den vorherigen Unterabschnitten 'Berechnung bei homogenen Bedingungen' und 'Berechnung bei günstigen Bedingungen' berechnet, und zwar ausgehend von folgenden Hypothesen:
- zs = zo,r,
- Gpath wird zwischen O und R berechnet.
Die Korrektur G'path braucht hier nicht berücksichtigt zu werden, da die betrachtete Quelle der Beugungspunkt ist. Deshalb ist vielmehr Gpath bei der Berechnung der Bodeneffekte zu verwenden, einschließlich für den unteren Grenzterm der Gleichung, der -3(1 - Gpath) wird.
Bei homogenen Bedingungen:  w= Gparth in Gleichung (2.5.17) und
w= Gparth in Gleichung (2.5.17) und  m= Gparth in Gleichung (2.5.18),
m= Gparth in Gleichung (2.5.18),
bei günstigen Bedingungen  m= Gparth in Gleichung (2.5.17) und
m= Gparth in Gleichung (2.5.17) und  w= Gparth in Gleichung (2.5.20),
w= Gparth in Gleichung (2.5.20),
- Δdif(S,R') ist die Dämpfung aufgrund der Beugung zwischen S und dem Spiegelempfänger R', berechnet wie im vorherigen Abschnitt 'Reine Beugung',
- Δdif(S,R) ist die Dämpfung aufgrund der Beugung zwischen S und R, berechnet wie im vorherigen Unterabschnitt 'Reine Beugung'.
Im Sonderfall, wenn der Empfänger unter der mittleren Bezugsebene liegt: Δdif(S,R') = Δdif(S,R) und Δground(O,R) = Aground(O,R)
Szenarien mit vertikalen Kanten
Die Gleichung (2.5.21) kann verwendet werden, um die Beugungen an vertikalen Kanten (seitliche Beugungen) bei Industrie-/Gewerbelärm zu berechnen. In diesem Fall wird Adif = Δdif(S,R) genommen und der Term Aground behalten. Weiterhin sind Aatm und Aground aus der Gesamtlänge des Ausbreitungsweges zu berechnen. Adiv wird nach wie vor aus der direkten Distanz d berechnet. Die Gleichungen (2.5.8) und (2.5.6) werden entsprechend zu:
|
| (2.5.33) |
|
| (2.5.34) |
Δdif wird tatsächlich bei homogenen Bedingungen in Gleichung (2.5.34) verwendet.
Eine seitliche Beugung wird nur in den Fällen berücksichtigt, in denen die folgenden Bedingungen erfüllt sind:
Die Quelle ist eine echte Punktquelle - nicht durch Segmentierung einer erweiterten Quelle wie einer Linien- oder Flächenquelle erzeugt.
Die Quelle ist keine Spiegelquelle, die zur Berechnung einer Reflexion konstruiert wurde.
Der Direktstrahl zwischen Quelle und Empfänger liegt vollständig über dem Geländeprofil.
In der vertikalen Ebene, die S und R enthält, ist die Weglängendifferenz δ größer als 0, d. h., der Direktstrahl ist blockiert. Daher kann in bestimmten Situationen bei homogenen Ausbreitungsbedingungen, nicht aber bei günstigen Ausbreitungsbedingungen, von einer seitlichen Beugung ausgegangen werden.
Sind alle genannten Bedingungen erfüllt, werden zusätzlich zum gebeugten Ausbreitungsweg in der vertikalen Ebene, in der die Quelle und der Empfänger enthalten sind, bis zu zwei Ausbreitungswege mit seitlicher Beugung berücksichtigt. Die seitliche Ebene ist definiert als die Ebene, die senkrecht zur vertikalen Ebene verläuft und außerdem die Quelle und den Empfänger enthält. Die Schnittflächen mit dieser seitlichen Ebene werden aus allen Hindernissen gebildet, die von dem von der Quelle bis zum Empfänger verlaufenden Direktstrahl durchbrochen werden. In der seitlichen Ebene definiert die kürzeste konvexe Verbindung zwischen Quelle und Empfänger, die aus geraden Segmenten besteht und diese Schnittflächen umfasst, die vertikalen Kanten, welche bei der Konstruktion des seitlich gebeugten Ausbreitungswegs berücksichtigt werden.
Zur Berechnung der Bodendämpfung für einen seitlich gebeugten Ausbreitungsweg wird die mittlere Bezugsebene zwischen Quelle und Empfänger unter Berücksichtigung des Bodenprofils senkrecht unter dem Ausbreitungsweg berechnet. Schneidet ein seitlicher Ausbreitungsweg bei der Projektion auf eine horizontale Ebene die Projektion eines Gebäudes, so wird dies bei der Berechnung von path (normalerweise mit = 0) und bei der Berechnung der mittleren Bezugsebene mit der vertikalen Höhe des Gebäudes berücksichtigt.
Reflexionen an vertikalen Hindernissen
Dämpfung durch Absorption
Die Reflexionen an vertikalen Hindernissen werden über Spiegelquellen erfasst. Somit werden Reflexionen an Gebäudefassaden und Lärmschutzwänden auf diese Weise erfasst.
Oberflächen von Objekten gelten nur dann als Reflektoren, wenn ihre Neigung bezogen auf die Senkrechte weniger als 15° beträgt. Reflexionen werden nur für Wege in der vertikalen Ausbreitungsebene berücksichtigt, d. h. nicht für seitlich gebeugte Wege. Für Einfalls- und Reflexionswege wird unter der Annahme, dass die reflektierende Oberfläche vertikal ist, der Reflexionspunkt (der auf dem reflektierenden Objekt liegt) bei homogenen Ausbreitungsbedingungen aus geraden Linien und bei günstigen Ausbreitungsbedingungen aus gekrümmten Linien gebildet. Die Höhe des Reflektors, gemessen durch den Reflexionspunkt und aus der Richtung des einfallenden Strahls betrachtet, muss mindestens 0,5 m betragen. Nach Projektion auf eine horizontale Ebene muss die Breite des Reflektors, gemessen durch den Reflexionspunkt und aus der Richtung des einfallenden Strahls betrachtet, mindestens 0,5 m betragen.
Die Hindernisse, bei denen mindestens eine Dimension unter 0,5 m liegt, sind - ausgenommen bei speziellen Konfigurationen - bei der Berechnung von Reflexionen außer Acht zu lassen. 2
Man beachte, dass Reflexionen am Boden hier nicht behandelt werden. Sie werden bei den Berechnungen der Dämpfung aufgrund der Begrenzung (Boden, Beugung) berücksichtigt.
Ist LWS der Leistungspegel der Quelle S und αr der Absorptionskoeffizient der Oberfläche des Hindernisses gemäß Definition in EN 1793-1:2013, dann ist der Leistungspegel der Spiegelquelle S' gleich:
| LWS2 = LWS + 10 · lg(1 - αr) = LWS + Arefl | (2.5.35) |
wobei 0 ≤ αr < 1.
Die oben beschriebenen Dämpfungen der Ausbreitung werden dann - wie beim direkten Ausbreitungsweg - auf diesen Ausbreitungsweg (Spiegelquelle, Empfänger) angewendet.
Abbildung 2.5.g Mit dem Spiegelquellverfahren erfasste spiegelnde Reflexion an einem Hindernis (S: Quelle, S': Spiegelquelle, R: Empfänger)
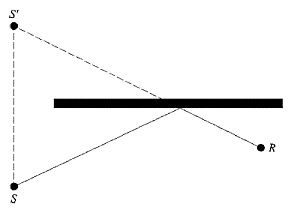
Dämpfung durch Retrobeugung
Bei der geometrischen Untersuchung von Schallausbreitungswegen während der Reflexion an einem vertikalen Hindernis (Schallschutzwand, Gebäude) bestimmt die Position des Auftreffens des Strahls in Bezug auf die Oberkante dieses Hindernisses über den mehr oder weniger erheblichen Anteil an Energie, der tatsächlich reflektiert wird. Dieser Verlust an akustischer Energie bei der Reflexion des Strahls wird als Dämpfung durch Retrobeugung bezeichnet.
Im Falle potenzieller Mehrfachreflexionen zwischen zwei vertikalen Wänden ist zumindest die erste Reflexion zu betrachten.
Im Falle eines Einschnitts (siehe zum Beispiel Abbildung 2.5.h) ist die Dämpfung durch Retrobeugung auf jede Reflexion an den Stützwänden anzuwenden.
Abbildung 2.5.h Vierfachreflexion eines Schallstrahls in Troglage: tatsächlicher Querschnitt (oben), aufgefalteter Querschnitt (unten)
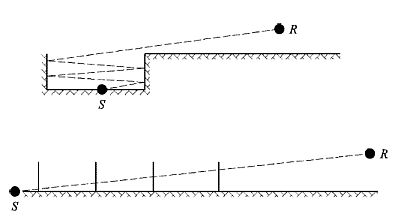
In dieser Darstellung erreicht der Schallstrahl den Empfänger, indem er die Stützwände des Einschnitts "nacheinander durchläuft", die daher mit Öffnungen verglichen werden können.
Bei der Berechnung der Ausbreitung durch eine Öffnung ist das Schallfeld beim Empfänger die Summe des Direktfeldes und des durch die Kanten der Öffnung gebeugten Feldes. Das gebeugte Feld sichert den stetigen Übergang zwischen dem freien Bereich und dem Schattenbereich. Erreicht der Strahl die Kante der Öffnung, ist das Direktfeld gedämpft. Die Berechnung entspricht der Berechnung der Dämpfung durch ein Hindernis im freien Bereich.
Die mit jeder Retrobeugung verbundene Weglängendifferenz δ' ist das Gegenstück zur Weglängendifferenz zwischen S und R jeweils an der Oberkante O, und dies in einer Ansicht mit einem entfalteten Querschnitt (siehe Abbildung 2.5.i).
| δ' = - (SO + OR - SR) | (2.5.36) |
Abbildung 2.5.i Die Weglängendifferenz für die zweite Reflexion
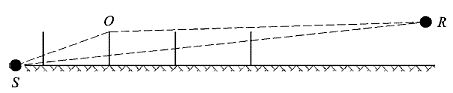
Das Minus-Zeichen in der Gleichung (2.5.36) bedeutet, dass der Empfänger hier im freien Bereich betrachtet wird.
Eine Dämpfung durch Retrobeugung Δretrodif wird anhand der Gleichung (2.5.37) ermittelt, die der Gleichung (2.5.21) mit neu gefassten Bezeichnungen ähnlich ist.
|
| (2.5.37) |
Diese Dämpfung betrifft den Direktstrahl jedes Mal, wenn er "durch" eine Wand oder ein Gebäude "verläuft" (reflektiert wird). Der Leistungspegel der Spiegelquelle S' wird so zu:
| LW2 = LW + 10 x lg(1 - ±r) - Δretrodif | (2.5.38) |
Bei komplexen Ausbreitungskonfigurationen können Beugungen zwischen Reflexionen oder zwischen dem Empfänger und den Reflexionen bestehen. In diesem Fall wird die Retrobeugung von den Wänden unter Berücksichtigung des Ausbreitungsweges zwischen der Quelle und dem ersten Beugungspunkt R' (daher in der Gleichung (2.5.36) als der Empfänger betrachtet) abgeschätzt. Dieses Prinzip veranschaulicht Abbildung 2.5.j.
Abbildung 2.5.j Weglängendifferenz in Anwesenheit einer Beugung: tatsächlicher Querschnitt (oben), aufgefalteter Querschnitt (unten)
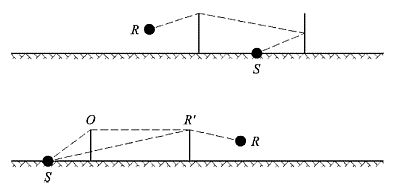
Im Falle von Mehrfachreflexionen werden die auf Einzelreflexionen zurückgehenden Reflexionen aufsummiert.
Wenn eine reflektierende Lärmschutzwand oder ein reflektierendes Hindernis in der Nähe des Eisenbahngleises vorhanden ist, werden die von der Quelle ausgehenden Schallstrahlen nacheinander von diesem Hindernis und von der seitlichen Fläche des Schienenfahrzeugs reflektiert. Unter diesen Bedingungen passieren die Schallstrahlen den Bereich zwischen dem Hindernis und dem Wagenkasten, bevor sie an der Oberkante des Hindernisses gebeugt werden.
Um Mehrfachreflexionen zwischen Schienenfahrzeug und einem nahe gelegenen Hindernis zu berücksichtigen, wird die Schallleistung einer einzelnen Ersatzschallquelle berechnet. Bei dieser Berechnung werden Bodeneffekte ignoriert.
Für die Ableitung der Schallleistung der Ersatzschallquelle gelten folgende Definitionen:
- Der Ursprung des Koordinatensystems ist die rechte Fahrfläche,
- eine reale Quelle befindet sich bei S (ds = 0, hs), wobei hs die Höhe der Quelle in Bezug auf die Fahrfläche ist,
- Die Ebene h = 0 definiert den Wagenkasten,
- ein vertikales Hindernis mit Oberkante in B (dB, hb),
- ein Empfänger, der sich in einer Entfernung dR > 0 hinter dem Hindernis befindet, wobei R die Koordinaten (dB+dR, hR) hat.
Die Innenseite des Hindernisses weist die Absorptionskoeffizienten α(f) pro Oktavband auf. Der Wagenkasten des Eisenbahnfahrzeugs hat einen entsprechenden Reflexionskoeffizienten Cref. Normalerweise ist Cref gleich 1. Nur bei offenen Flachgüterwagen kann der Wert 0 verwendet werden. Bei dB > 5hB oder α(f) > 0,8 wird keine Wechselwirkung zwischen Zug und Hindernis berücksichtigt.
In dieser Konfiguration können mehrere Reflexionen zwischen dem Wagenkasten und dem Hindernis mithilfe von Spiegelquellen an Position Sn (dn = -2n. dB, hn = hs), n = 0, 1, 2..N, berechnet werden, wie in Abbildung 2.5.k dargestellt.
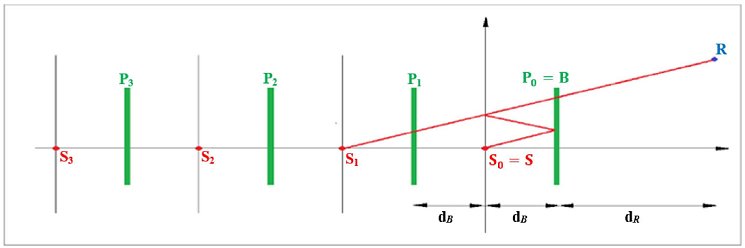
Die Schallleistung der Ersatzschallquelle wird ausgedrückt durch:
|
|
(2.5.39) |
Wobei die Schallleistung der Teilquellen gegeben ist durch:
LW,n = LW + ΔLn
ΔLn = ΔLgeo,n + ΔLdif,n + ΔLabs,n + ΔLref,n + ΔLretrodif,n
Dabei gilt:
| LW | Schallleistung der realen Schallquelle |
| ΔLgeo,n | ein Korrekturterm für die sphärische Divergenz |
| ΔLdif,n | ein Korrekturterm für die Beugung an der Oberkante des Hindernisses |
| ΔLabs,n | ein Korrekturterm für die Absorption an der Innenseite des Hindernisses |
| ΔLref,n | ein Korrekturterm für die Reflexion vom Wagenkasten |
| ΔLretrodif,n | ein Korrekturterm für die endliche Höhe des als Reflektor agierenden Hindernisses |
Die Korrektur für die sphärische Divergenz ergibt sich aus:
|
|
(2.5.40) |
|
|
(2.5.41) |
Die Korrektur für die Beugung an der Oberkante des Hindernisses ergibt sich aus:
(2.5.42)
|
ΔLdif,n = D0 - Dn |
(2.5.42) |
Dabei ist Dn die Dämpfung aufgrund von Beugung, berechnet nach Gleichung (2.5.21) mit C'' = 1, für den Weg von der Quelle Sn zum Empfänger R unter Berücksichtigung der Beugung an der Oberkante von Hindernis B:
|
δn = ±(| SnB| + | BR| - | SnR|) |
(2.5.43) |
Die Korrektur für die Absorption an der Innenseite des Hindernisses ergibt sich aus:
|
ΔLabs,n = 10 • n • lg (1-α) |
(2.5.44) |
Die Korrektur für die vom Wagenkasten ausgehende Reflexion ergibt sich aus:
|
Δ Lref,n = 10 • n • lg (Cref) |
(2.5.45) |
Die Korrektur für die endliche Höhe des reflektierenden Hindernisses wird durch die Retrobeugung berücksichtigt. Der Weg des Strahls, der einem Spiegelbild in der Größenordnung N > 0 entspricht, wird n-mal vom Hindernis reflektiert. Im Querschnitt finden diese Reflexionen in den Entfernungen
di = - (2i-q) db, i = 1,2,..n statt. Hierbei bezeichnet Pi(d = di, h = hb), i = 1,2,..n die Oberkanten dieser reflektierenden Oberflächen. An jedem dieser Punkte wird ein Korrekturterm wie folgt berechnet:
|
|
(2.5.46) |
Hierbei wird Δretrodif,n,i für eine Quelle an Position Sn, eine Hindernisoberkante bei Pi und einen Empfänger an Position R' berechnet. Die Position des äquivalenten Empfängers R' wird durch R' = R angegeben, wenn der Empfänger über der Sichtlinie von Sn zu B liegt; andernfalls wird die Position des äquivalenten Empfängers auf der vertikal über dem tatsächlichen Empfänger verlaufenden Sichtlinie angenommen, und zwar:
|
dR' = dR |
(2.5.47) |
|
|
(2.5.48) |
 | weiter . |  |
...
X
⍂
↑
↓