umwelt-online: DIN 1045-1 Tragwerke aus Beton, Stahlbeton und Spannbeton; Bemessung und Konstruktion (10)
 | zurück |  |
Tabelle 20 - Grenzdurchmesser ds* bei Betonstählen
| Zeile | Spalte | 1 | 2 | 3 |
| Stahlspannung σs N/mm2 | Grenzdurchmesser der Stäbe in mm in Abhängigkeit vom Rechenwert der Rissbreite wk | |||
| wk = 0,4 mm | wk = 0,3 mm | wk = 0,2 mm | ||
| 1 | 160 | 56 | 42 | 28 |
| 2 | 200 | 36 | 28 | 18 |
| 3 | 240 | 25 | 19 | 13 |
| 4 | 280 | 18 | 14 | 9 |
| 5 | 320 | 14 | 11 | 7 |
| 6 | 360 | 11 | 8 | 6 |
| 7 | 400 | 9 | 7 | 5 |
| 8 | 450 | 7 | 5 | 4 |
Tabelle 21 - Höchstwerte der Stababstände von Betonstählen
| Zeile | Spalte | 1 | 2 | 3 |
| Stahlspannung σs N/mm2 | Höchstwerte der Stababstände in mm in Abhängigkeit vom Rechenwert der Rissbreite wk | |||
| wk = 0,4 mm | wk = 0,3 mm | wk = 0,2 mm | ||
| 1 | 160 | 300 | 300 | 200 |
| 2 | 200 | 300 | 250 | 150 |
| 3 | 240 | 250 | 200 | 100 |
| 4 | 280 | 200 | 150 | 50 |
| 5 | 320 | 150 | 100 | - |
| 6 | 360 | 100 | 50 | - |
(5) Bei Bauteilen mit im Verbund liegenden Spanngliedern ist die Betonstahlspannung für die maßgebende Einwirkungskombination unter Berücksichtigung des unterschiedlichen Verbundverhaltens von Betonstahl und Spannstahl nach Gleichung (132) zu berechnen.
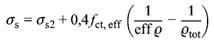 | (132) |
Dabei ist
| σs2 | die Spannung im Betonstahl bzw. der Spannungszuwachs im Spannstahl im Zustand II für die maßgebende Einwirkungskombination unter Annahme eines starren Verbundes | |
| eff ρ | der effektive Bewehrungsgrad unter Berücksichtigung der unterschiedlichen Verbundfestigkeiten | |
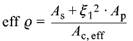 | (133) | |
| ρtot | der geometrische Bewehrungsgrad | |
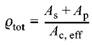 | (134) | |
| As | die Querschnittsfläche der Betonstahlbewehrung, siehe Legende zu Gleichung (127) | |
| Ap | die Querschnittsfläche der Spannglieder, die im Wirkungsbereich Ac, eff der Bewehrung liegen | |
| Ac, eff | der Wirkungsbereich der Bewehrung nach Bild 53 | |
| ξ1 | das Verhältnis der Verbundfestigkeiten nach Gleichung (130) | |
| fct, eff | die wirksame Betonzugfestigkeit nach 11.2.2 (5) |
Bild 53 - Wirkungsbereich Ac, eff der Bewehrung
Legende
| a) | Balken |
| b) | Platten (x ist die Höhe der Druckzone im Zustand I) |
| c) | Bauteil unter Zugbeanspruchung |
| 1 | Wirkungsbereich der Bewehrung Ac, eff |
| 2 | Schwerachse der Bewehrung |
(6) Werden in einem Querschnitt Stäbe mit unterschiedlichen Durchmessern verwendet, darf ein mittlerer Stabdurchmesser dsm = ∑ds, i2/∑ds, i angesetzt werden.
(7) Bei Stabbündeln ist anstelle des Stabdurchmessers der Einzelstäbe der Vergleichsdurchmesser des Stabbündels nach 12.9 (2) anzusetzen.
(8) Bei Betonstahlmatten mit Doppelstäben darf der Durchmesser eines Einzelstabes angesetzt werden.
(9) Die Begrenzung der Schubrissbreite darf ohne weiteren Nachweis als sichergestellt angenommen werden, wenn die Bewehrungsrichtlinien nach 13.2.3 und 13.3.3 eingehalten sind.
11.2.4 Berechnung der Rissbreite
(1) Die Begrenzung der Rissbreite darf auch durch eine direkte Berechnung nachgewiesen werden. Für den Rechenwert der Rissbreite wk gilt:
| wk = sr, max * (εsm - εcm) | (135) |
Dabei ist
| wk | der Rechenwert der Rissbreite |
| sr, max | der maximale Rissabstand bei abgeschlossenem Rissbild |
| εsm | die mittlere Dehnung der Bewehrung unter der maßgebenden Einwirkungskombination unter Berücksichtigung der Mitwirkung des Betons auf Zug zwischen den Rissen |
| εcm | die mittlere Dehnung des Betons zwischen den Rissen |
(2) Die Differenz der mittleren Dehnungen von Beton und Betonstahl darf wie folgt berechnet werden:
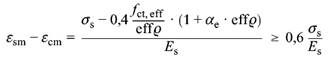 | (136) |
Dabei ist
| αc | das Verhältnis der Elastizitätsmoduln
αc = Es/Ecm |
| effρ | der effektive Bewehrungsgrad nach Gleichung (133) |
| fct, eff | die wirksame Betonzugfestigkeit nach 11.2.2 (5) |
| σs | die Betonstahlspannung im Riss. Bei Bauteilen mit Vorspannung im Verbund ist 11.2.3 (5) zu berücksichtigen |
(3) Bei Bauteilen, die nur im Bauteil selbst hervorgerufenem Zwang unterworfen sind (z.B. infolge Abfließen der Hydratationswärme) darf (εsm - εcm) unter Ansatz von σs = σsr ermittelt werden. Dabei ist σsr diejenige Spannung in der Zugbewehrung, die auf der Grundlage eines gerissenen Querschnitts für eine Einwirkungskombination berechnet wird, die zur Erstrissbildung führt.
(4) Der maximale Rissabstand darf nach Gleichung (137) berechnet werden:
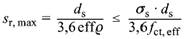 | (137) |
Dabei ist
| effρ | der effektive Bewehrungsgrad nach Gleichung (133) |
| ds | der Stabdurchmesser des Betonstahls. Werden in einem Querschnitt Stäbe mit unterschiedlichen Durchmessern, Stabbündel oder Doppelstäbe verwendet, gelten 11.2.3 (6), (7) und (8) |
Bei Mattenbewehrung muss der Rissabstand nicht größer als die doppelte Maschenweite angenommen werden.
(5) Wenn Risse in orthogonal bewehrten Bauteilen einen Winkel von mehr als 15° zur Richtung der zugeordneten Bewehrung bilden, darf der Rissabstand nach Gleichung (138) berechnet werden:
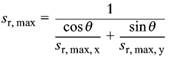 | (138) |
Dabei ist
| θ | der Winkel zwischen der Bewehrung in x-Richtung und der Richtung der Hauptzugspannung |
| sr, max, x, sr, max, y | der jeweilige maximale Rissabstand in x- und y-Richtung nach Gleichung (137) |
(6) Wenn die Rissbreiten für Beanspruchungen berechnet werden, bei denen die Zugspannungen aus einer Kombination von Zwang und Lastbeanspruchung herrühren, dürfen die Gleichungen dieses Abschnitts verwendet werden. Jedoch sollte die Dehnung infolge Lastbeanspruchung, die auf Grundlage eines gerissenen Querschnitts berechnet wurde, um den Wert infolge Zwang erhöht werden.
(7) In Fällen, in denen die resultierende Zwangdehnung 0,8 o/oo nicht überschreitet, ist es im Allgemeinen ausreichend, die Rissbreite für den größeren Wert der Spannung aus Zwang- oder Lastbeanspruchung zu ermitteln.
(8) Wenn in Bereichen, für die der Nachweis der Rissbreitenbegrenzung geführt wird, keine oder keine ausreichende im Verbund liegende Bewehrung vorhanden ist, sollte ein oberer Grenzwert der Rissbreite festgelegt werden. In diesen Fällen darf der maximale Rissabstand gleich der doppelten Risstiefe gesetzt werden. Ein Beispiel hierfür sind Wände, bei denen die mit dem Abfließen der Hydratationswärme verbundene Verformung durch früher hergestellte Fundamente behindert wird. In diesem Fall darf sr, max gleich der zweifachen Wandhöhe gesetzt werden.
11.3 Begrenzung der Verformungen
11.3.1 Allgemeines
(1) Die Verformungen eines Bauteils oder eines Tragwerks dürfen weder die ordnungsgemäße Funktion noch das Erscheinungsbild des Bauteils selbst oder angrenzender Bauteile (z.B. leichte Trennwände, Verglasungen, Außenwandverkleidungen, haustechnische Anlagen) beeinträchtigen.
(2) Verformungen dürfen die ordnungsgemäße Funktion von Maschinen oder Geräten auf dem Tragwerk nicht beeinträchtigen. Dies wird in dieser Norm nicht behandelt.
(3) In diesem Abschnitt werden nur Verformungen in vertikaler Richtung von biegebeanspruchten Bauteilen behandelt. Dabei wird unterschieden in
- Durchhang: vertikale Bauteilverformung bezogen auf die Verbindungslinie der Unterstützungspunkte,
- Durchbiegung: vertikale Bauteilverformung bezogen auf die Systemlinie des Bauteils (z.B. bei Schalungsüberhöhungen bezogen auf die überhöhte Lage).
(4) Von Fall zu Fall kann es erforderlich sein, auch andere Verformungen außer Biegeverformungen zu betrachten, z.B. Schubverformungen, Verdrehungen und Teilverkürzungen von vertikalen Bauteilen; im Allgemeinen dürfen diese aber vernachlässigt werden.
(5) Die aus dynamischen Einwirkungen resultierenden Verformungen werden in dieser Norm nicht behandelt.
(6) Die Grenzen für die Verformung müssen unter Berücksichtigung der Art des Tragwerks, der Oberflächenausbildung angrenzender Bauteile sowie der Funktion des Tragwerks festgelegt werden. Sofern keine besonderen (erhöhten oder verminderten) Anforderungen vorliegen, gelten die nachfolgenden Richtwerte.
(7) Die folgenden Verformungsgrenzen stellen im Allgemeinen hinreichende Gebrauchseigenschaften von Bauwerken, wie z.B. Wohnbauten, Bürobauten, öffentlichen Bauten und Fabriken, sicher. Sofern besondere Verhältnisse die Verwendung der folgenden Richtwerte für ein bestimmtes Tragwerk einschränken, sind Grenzwerte mit dem Bauherren zu vereinbaren.
(8) Es darf angenommen werden, dass das Erscheinungsbild und die Gebrauchstauglichkeit eines Tragwerks nicht beeinträchtigt werden, wenn der Durchhang eines Balkens, einer Platte oder eines Kragbalkens unter der quasi-ständigen Einwirkungskombination 1/250 der Stützweite nicht überschreitet (bei Kragträgern ist für die Stützweite die 2, 5fache Kraglänge anzusetzen). In Fällen, in denen der Durchhang weder die Gebrauchstauglichkeit beeinträchtigt noch besondere Anforderungen an das Erscheinungsbild gestellt werden, darf dieser Wert erhöht werden.
(9) Überhöhungen sind zulässig, um einen Teil oder den gesamten Durchhang auszugleichen. Die Schalungsüberhöhung sollte im Allgemeinen 1/250 der Stützweite nicht überschreiten.
(10) Schäden an angrenzenden Bauteilen (z.B. an leichten Trennwänden) können auftreten, wenn die nach dem Einbau dieser Bauteile auftretende Durchbiegung einschließlich der zeitabhängigen Verformungen übermäßig groß ist. Als Richtwert für die Begrenzung darf 1/500 der Stützweite angenommen werden. Diese Grenze darf heraufgesetzt werden, wenn das Bauteil, das Schaden nehmen kann, so bemessen ist, dass größere Durchbiegungen verträglich sind, oder wenn es in der Lage ist, größere Durchbiegungen ohne Schaden aufzunehmen.
11.3.2 Nachweis der Begrenzung der Verformungen von Stahlbetonbauteilen ohne direkte Berechnung
(1) Der Nachweis der Begrenzung der Durchbiegung darf für Stahlbetonbauteile vereinfacht durch eine Begrenzung der Biegeschlankheit li/d geführt werden.
(2) Für Deckenplatten des üblichen Hochbaus ist bei Normalbeton im Allgemeinen eine Begrenzung der Biegeschlankheit auf den Wert li/d < 35 ausreichend. Für Deckenplatten des üblichen Hochbaus, an die höhere Anforderungen im Hinblick auf die Begrenzung der Durchbiegung gestellt werden (siehe auch 11.3.1 (10)), sollte jedoch die Biegeschlankheit nicht größer als li/d < 150 / li (mit li in m) gewählt werden. Für Leichtbeton sind diese Grenzwerte mit dem Faktor ηE0,15 (mit ηE nach Tabelle 10) abzumindern.
(3) Bei biegebeanspruchten Bauteilen, deren Durchbiegung vorwiegend durch die im betrachteten Feld wirkende Belastung verursacht wird, darf die Ersatzstützweite mit li = α * leff in Rechnung gestellt werden. Der Beiwert α kann für häufig vorkommende Anwendungsfälle aus Tabelle 22 entnommen werden. Bei linienförmig gelagerten, rechteckigen Platten ist die kleinere der beiden Ersatzstützweiten ll maßgebend, bei punktförmig gelagerten Platten (Flachdecken) die größere.
(4) Rand- und Innenfelder durchlaufender Bauteile dürfen nach Tabelle 22, Zeile 2 bzw. 3 behandelt werden, sofern das Verhältnis angrenzender effektiver Stützweiten im Bereich 0,8 < leff, 1 / leff, 2 < 1,25 liegt.
Tabelle 22 - Beiwerte A zur Bestimmung der Ersatzstützweite
| Spalte | 1 | 2 |
| Zeile | Statisches System | α = li / leff |
| 1 | 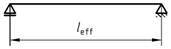 | 1,00 |
| 2 | 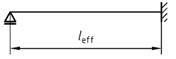 | 0,80 |
| 3 | 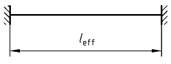 | 0,60 |
| 4 | 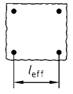 | Innenfeld 0,70 a
Randfeld 0,90 a |
| 5 | 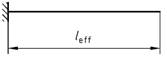 | 2,4 |
| a | Bei Platten mit Beton ab der Festigkeitsklasse C30/37 dürfen diese Werte um 0,1 abgemindert werden. |
12 Allgemeine Bewehrungsregeln
12.1 Allgemeines
(1) Die in diesem Abschnitt aufgeführten Festlegungen gelten für Betonstabstähle, Spannglieder und, sofern nicht anders geregelt, für Betonstahlmatten bei vorwiegend ruhenden und nicht vorwiegend ruhenden Einwirkungen. Die besonderen Regelungen für Stabbündel enthält 12.9. Betonstahlmatten mit Doppelstäben sind, sofern nicht anders geregelt, wie Stabbündel zu behandeln.
(2) Die in den Grenzzuständen der Tragfähigkeit und in den Grenzzuständen der Gebrauchstauglichkeit erforderlichen Bewehrungen sind jeweils nach den Festlegungen dieses Abschnitts zu verankern und gegebenenfalls zu stoßen.
(3) Stäbe mit ds > 32 mm dürfen nur in Bauteilen mit einer Mindestdicke von 15 ds verwendet werden.
12.2 Stababstände von Betonstählen
(1) Der Stababstand muss mindestens so groß sein, dass der Beton eingebracht und ausreichend verdichtet werden kann sowie ein ausreichender Verbund zwischen Betonstahl und Beton sichergestellt ist.
(2) Der lichte Abstand (horizontal und vertikal) zwischen parallelen Einzelstäben oder Lagen paralleler Stäbe darf nicht unter 20 mm liegen, muss jedoch mindestens gleich dem Durchmesser des größten Stabes sein. Sofern nicht besondere Maßnahmen zum Einbringen und Verdichten des Betons getroffen werden, dürfen diese Abstände bei einem Größtkorndurchmesser der Gesteinskörnung dg > 16 mm nicht kleiner als dg + 5 mm sein.
(3) Bei einer Stabanordnung in getrennten horizontalen Lagen sollten die Stäbe jeder einzelnen Lage vertikal übereinander liegen, und es sollten ausreichende Lücken zum Einbringen eines Innenrüttlers vorgesehen werden.
(4) Für übergreifende Stäbe ist 12.8.1 zu beachten.
12.3 Biegen von Betonstählen
12.3.1 Biegerollendurchmesser
(1) Der kleinste Biegerollendurchmesser eines Stabes muss so festgelegt werden, dass Betonabplatzungen oder Zerstörungen des Betongefüges im Bereich der Biegung und Risse im Bewehrungsstab infolge des Biegens ausgeschlossen werden.
(2) Die Mindestwerte der Biegerollendurchmesser nach Tabelle 23 sind einzuhalten. Bei Leichtbeton sind die Werte um 30 % zu vergrößern.
Tabelle 23 - Mindestwerte der Biegerollendurchmesser dbr
| Spalte | 1 | 2 | 3 | 4 | 5 | |
| Zeile | Haken, Winkelhaken, Schlaufen | Schrägstäbe oder andere gebogene Stäbe | ||||
| Stabdurchmesser | Mindestwerte der Betondeckung rechtwinklig zur Biegeebene | |||||
| ds < 20 mm | ds > 20 mm | > 100 mm > 7 ds | > 50 mm > 3 ds | d 50 mm d 30 ds | ||
| 1 | Mindestwerte der Biegerollendurchmesser dbr | 4 ds | 7 ds | 10 ds | 15 ds | 20 ds |
(3) Für Betonstahlmatten und geschweißte Bewehrung, die nach dem Schweißen gebogen werden, gelten zusätzlich die Mindestwerte der Biegerollendurchmesser nach Tabelle 24.
Tabelle 24 - Mindestwerte der Biegerollendurchmesser dbr für nach dem Schweißen gebogene Bewehrung
| Spalte | 1 | 2 | 3 | 4 | |
| Zeile | vorwiegend ruhende Einwirkungen | nicht vorwiegend ruhende Einwirkungen | |||
| Schweißung außerhalb des Biegebereiches | Schweißung innerhalb des Biegebereiches | Schweißung auf der Außenseite der Biegung | Schweißung auf der Innenseite der Biegung | ||
| 1 | für a < 4d, | 20 ds | 20 ds | 100 ds | 500 ds |
| 2 | für a > 4 ds | Werte nach Tabelle 23 | |||
| a | Abstand zwischen Biegeanfang und Schweißstelle |
12.3.2 Hin- und Zurückbiegen
(1) Das Hin- und Zurückbiegen von Betonstählen stellt für den Betonstahl und den umgebenden Beton eine zusätzliche Beanspruchung dar.
(2) Beim Kaltbiegen von Betonstählen sind die folgenden Bedingungen einzuhalten:
- Der Stabdurchmesser darf höchstens ds = 14 mm sein. Ein Mehrfachbiegen, bei dem das Hin- und Zurückbiegen an derselben Stelle wiederholt wird, ist nicht zulässig.
- Bei vorwiegend ruhenden Einwirkungen muss der Biegerollendurchmesser beim Hinbiegen mindestens 6 ds betragen. Die Bewehrung darf im Grenzzustand der Tragfähigkeit höchstens zu 80 % ausgenutzt werden.
- Bei nicht vorwiegend ruhender Belastung muss der Biegerollendurchmesser beim Hinbiegen mindestens 15 ds betragen. Die Schwingbreite der Stahlspannung darf 50N/mm2 nicht überschreiten.
- Verwahrkästen für Bewehrungsanschlüsse sind so auszubilden, dass sie weder die Tragfähigkeit des Betonquerschnitts noch den Korrosionsschutz der Bewehrung beeinträchtigen.
- Im Bereich der Rückbiegestelle ist die Querkraft auf 0,6 VRd, max (mit VRd, max nach 10.3.4) zu begrenzen.
(3) Beim Warmhinbiegen und Warmzurückbiegen von Betonstählen sind die folgenden Bedingungen einzuhalten:
- Wird Betonstahl bei der Verarbeitung warm gebogen (> 500°C), so darf er nur mit einer rechnerischen Streckgrenze von 220 N/mm2 in Rechnung gestellt werden.
- Bei nicht vorwiegend ruhenden Einwirkungen darf die Schwingbreite der Stahlspannung 50N/mm2 nicht überschreiten.
(4) Einzelheiten der technischen Ausführung sind z.B. im DBV-Merkblatt "Rückbiegen von Betonstahl und Anforderungen an Verwahrkästen" enthalten.
12.4 Verbundbedingungen
(1) Die Qualität des Verbunds hängt wesentlich von der Oberflächengestalt des Betonstahls, den Abmessungen des Bauteils sowie der Lage und dem Neigungswinkel der Bewehrung während des Betonierens ab.
(2) Die Verbundbedingungen sind als gut anzusehen für
- alle Stäbe mit einer Neigung α von 45° bis 90° zur Waagerechten während des Betonierens (siehe Bild 54 a)),
- alle Stäbe mit einer Neigung α von 0° bis 45° zur Waagerechten während des Betonierens, die
- in Bauteile eingebaut sind, deren Dicke in Betonierrichtung 300 mm nicht überschreitet (siehe Bild 54 b)),
- in Bauteile mit einer Dicke größer als 300 mm eingebaut sind und entweder höchstens 300 mm über der Unterkante des Frischbetons (siehe Bild 54 c)) oder mindestens 300 mm unter der Oberseite des Bauteils oder eines Betonierabschnittes liegen (siehe Bild 54 d)),
- liegend gefertigte stabförmige Bauteile (z.B. Stützen), die mit einem Außenrüttler verdichtet werden und deren äußere Querschnittsabmessungen 500 mm nicht überschreiten.
(3) In allen anderen Fällen sind die Verbundbedingungen als mäßig anzusehen.
(4) In Bauteilen, die im Gleitbauverfahren hergestellt werden, sind die Verbundbedingungen für alle Stäbe als mäßig anzusehen.
Bild 54 - Verbundbedingungen
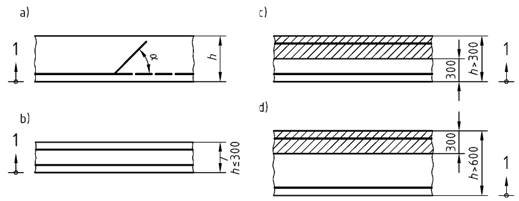
Legende
| a) und b) | gute Verbundbedingungen für alle Stäbe | |
| c) und d) | Stäbe im nichtschraffierten Bereich: | gute Verbundbedingungen; |
| Stäbe im schraffierten Bereich: | mäßige Verbundbedingungen | |
| 1 Betonierrichtung | ||
12.5 Bemessungswert der Verbundspannung
(1) Der Grenzwert der aufnehmbaren Verbundspannung stellt sicher, dass im Grenzzustand der Tragfähigkeit ein ausreichender Sicherheitsabstand gegen das Versagen des Verbunds vorliegt und im Grenzzustand der Gebrauchstauglichkeit keine wesentliche Verschiebung zwischen Stahl und Beton auftritt.
(2) Für gute Verbundbedingungen sind die Bemessungswerte der Verbundspannung fbd in Tabelle 25 angegeben.
Die Werte in Tabelle 25 ergeben sich mit γc nach 5.3.3 aus:
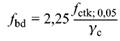 | (139) |
Für mäßige Verbundbedingungen sind die Werte nach Tabelle 25 mit dem Faktor 0,7 zu multiplizieren.
(3) Bei Leichtbeton sind die Werte fbd der Tabelle 25 mit dem Faktor η1 nach Tabelle 10 zu multiplizieren.
Tabelle 25 - Bemessungswerte der Verbundspannung fbd für Betonstahl bei guten Verbundbedingungen und ds d 32 mm
| Zeile | Spalte | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 110 | 11 | 12 | 13 | 14 | 15 |
| charakteristische Betondruckfestigkeit fck in N/mm2 | ||||||||||||||||
| 12 | 16 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 70 | 80 | 90 | 100 | ||
| 1 | fbd N/mm2 | 1,6 | 2,0 | 2,3 | 2,7 | 3,0 | 3,4 | 3,7 | 4,0 | 4,3 | 4,4 | 4,5 | 4,7 | 4,8 | 4,9 | 4,9 |
(4) Bei Stabdurchmessern ds > 32mm sind die Werte fbd nach Tabelle 25 mit dem Faktor (132 - ds)/100 zu multiplizieren (mit ds in mm).Bei Leichtbeton muß die verwendung soclehr Stäbe aufgrund von Erfahrungen oder Versuchsergebnissen gerechtfertigt sein.
Die Werte fbd nach Tabelle 25 sind dann mit dem Faktor n1(132 - ds)/100 zu multiplizieren (η1 nach Tabelle 10).
(5) Die Werte nach Tabelle 25 dürfen in den folgenden Fällen erhöht werden, wobei nur eine der beiden Möglichkeiten in Ansatz gebracht werden darf.
- Ist ein Querdruck p rechtwinklig zur Bewehrungsebene vorhanden, ist eine Erhöhung mit dem Faktor 1/(1 - 0,04p) < 1,5 zulässig. Für p ist der mittlere Querdruck im Verankerungs- oder Übergreifungsbereich in N/mm2 einzusetzen.
- Falls eine allseitige, durch Bewehrung gesicherte Betondeckung von mindestens 10ds vorhanden ist, beträgt die zulässige Erhöhung 50 %. Dies gilt nicht für Übergreifungsstöße mit einem Achsabstand der Stöße nach Bild 57 von s < 10ds.
(6) Die Werte nach Tabelle 25 sind um 1/3 abzumindern, wenn rechtwinklig zur Bewehrungsebene ein Querzug vorhanden ist, der eine Rissbildung parallel zur Bewehrungsstabachse im Verankerungsbereich erwarten lässt. 12) Wird bei vorwiegend ruhenden Einwirkungen die Breite der Risse parallel zu den Stäben auf wk < 0,2 mm begrenzt, darf auf diese Abminderung verzichtet werden.
12.6 Verankerung der Längsbewehrung
12.6.1 Allgemeines zu den Verankerungsarten
(1) Bewehrungsstäbe oder geschweißte Betonstahlmatten müssen so verankert sein, dass ihre Kräfte in den Beton eingeleitet werden und eine Längsrissbildung und ein Abplatzen des Betons im Verankerungsbereich ausgeschlossen sind. Die erforderliche Querbewehrung ist in 12.6.3 geregelt.
(2) Die zulässigen Verankerungsarten zeigt Tabelle 26.
(3) Für Druckbewehrungen sind Haken, Winkelhaken oder Schlaufen nicht zulässig.
(4) Stäbe mit ds > 32 mm müssen als gerade Stäbe oder mit Ankerkörpern verankert werden.
(5) Zur Einleitung konzentrierter Verankerungskräfte in den Beton siehe 13.9.
(6) Sofern rechnerisch nicht nachweisbar, sind Ankerkörper durch allgemeine bauaufsichtliche Zulassungen zu regeln.
12.6.2 Verankerungslänge
(1) Das Grundmaß der Verankerungslänge ist die gerade Verankerungslänge, die für die Verankerung der Stabkraft Fsd = As * fyd (mit fyd = fyk/γs) bei Annahme einer über die Verankerungslänge und den Stabumfang konstanten Verbundspannung fbd nach 12.5 erforderlich ist.
(2) Das Grundmaß der Verankerungslänge für die Verankerung eines Einzelstabes ist:
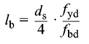 | (140) |
(3) Die erforderliche Verankerungslänge darf berechnet werden aus:
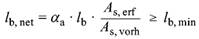 | (141) |
Dabei ist
| As, erf, As, vorh | die rechnerisch erforderliche bzw. die vorhandene Querschnittsfläche der Bewehrung |
| lb, min | der Mindestwert der Verankerungslänge: | |
| lb, min = 0,3αa * lb > 10ds | für Verankerungen von Zugstäben | |
| lb, min = 0,6lb > 10ds | für Verankerungen von Druckstäben |
| α a | der Beiwert zur Berücksichtigung der Wirksamkeit der Verankerungsarten nach Tabelle 26 |
(4) Die für die Zugkraftdeckung erforderlichen Verankerungslängen von Betonstahl sind in 13.2.2 geregelt.
(5) Für die Verankerung von Spanngliedern im sofortigen Verbund gilt 8.7.6.
12.6.3 Erforderliche Querbewehrung
(1) Im Verankerungsbereich von Bewehrungsstäben müssen die infolge einer Sprengwirkung auftretenden örtlichen Querzugspannungen im Beton durch Querbewehrung aufgenommen werden.
(2) Die Anforderungen nach Absatz (1) gilt als erfüllt, wenn
- konstruktive Maßnahmen oder andere günstige Einflüsse (z.B. Querdruck) ein Spalten des Betons verhindern,
- die nach Abschnitt 13 mindestens erforderlichen Bügel (bei Balken oder Stützen) oder Querbewehrungen (bei Platten oder Wänden) angeordnet werden.
(3) Bei Stabdurchmessern ds > 32 mm ohne Querdruck im Verankerungsbereich ist eine zusätzliche Querbewehrung nach Bild 55 erforderlich. Sie darf nicht geringer sein als nachstehend festgelegt:
- parallel zur Bauteiloberfläche:
Ast = n1 * 0,25As (142) - rechtwinklig zur Bauteiloberfläche:
Asv = n2 * 0,25As (143)
Dabei ist
| As | die Querschnittsfläche eines verankerten Stabes |
| n1 | die Anzahl der Bewehrungslagen, die im gleichen Schnitt verankert werden |
| n2 | die Anzahl der Bewehrungsstäbe, die in jeder Lage verankert werden |
Die Querbewehrung muss in Abständen, die näherungsweise dem fünffachen Stabdurchmesser der verankerten Bewehrung entsprechen, gleichmäßig über den Verankerungsbereich verteilt sein. 13)
Bild 55 - Zusatzbewehrung im Verankerungsbereich ohne Querdruck bei Stabdurchmessern ds > 32 mm
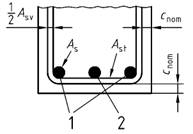
Legende
| 1 | verankerte Bewehrungsstäbe |
| 2 | durchlaufender Bewehrungsstab |
Tabelle 26 - Zulässige Verankerungsarten von Betonstahl
| 1 | 2 | 3 | |||
| Art und Ausbildung der Verankerung | Beiwert αa | ||||
| Zugstäbe a | Druckstäbe | ||||
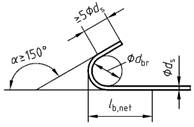
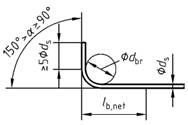
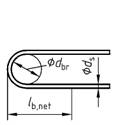
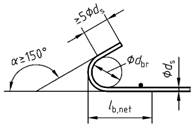
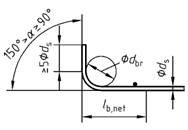
| 1 | a) Gerade Stabenden | 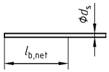 | 1,0 c | 1,0 c | |
| 2 | b) Haken
| c) Winkelhaken
| d) Schlaufen
| 0,7 b
(1,0) | - |
| 3 | e) Gerade Stabenden mit mindestens einem angeschweißten Stab innerhalb lb, net | 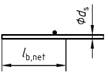 | 0,7 | 0,7 | |
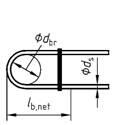
| 4 | f) Haken
| g) Winkelhaken
| h) Schlaufen
(Draufsicht)
| 0,5
(0,7) | - |
| mit jeweils mindestens einem angeschweißten Stab innerhalb lb, net vor dem Krümmungsbeginn | |||||
| 5 | i) Gerade Stabenden mit mindestens zwei angeschweißten Stäben innerhalb lb, net (Stababstand s < 100 mm und > 5ds und > 50 mm) nur zulässig bei Einzelstäben mit ds < 16 mm und bei Doppelstäben mit ds < 12 mm | 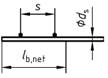 | 0,5 | 0,5 | |
| a | Die in Spalte 2 in Klammern angegebenen Werte gelten, wenn im Krümmungsbereich rechtwinklig zur Krümmungsebene die Betondeckung weniger als 3ds beträgt oder kein Querdruck oder keine enge Verbügelung vorhanden ist. |
| b | Bei Schlaufenverankerungen mit Biegerollendurchmesser dbr > 15 ds darf der Wert αa auf 0,5 reduziert werden. |
 | weiter. |  |
...
X
⍂
↑
↓