

umwelt-online: Richtlinie 2002/49/EG über die Bewertung und Bekämpfung von Umgebungslärm - Anhang II (3)
 | zurück |  |
| Datenanforderungen | Anlage A |
In Abschnitt 2.7.6 des Haupttextes werden in allgemeinen Worten die Anforderungen an fallspezifische Flughafen- und Flughafenbetriebsdaten beschrieben, die für die Berechnung von Lärmkonturen benötigt werden. Die folgenden Datenblätter enthalten Beispieldaten für einen hypothetisch angenommenen Flughafen. Die speziellen Formate der Daten hängen generell von den Anforderungen und Erfordernissen des jeweiligen Lärmmodellierungssystems und Untersuchungsszenarios ab.
Anmerkung: Es wird empfohlen, geografische Informationen (Bezugspunkte usw.) in kartesischen Koordinaten anzugeben. Die Auswahl des entsprechenden Koordinatensystems hängt in der Regel davon ab, was für Karten verfügbar sind.
A1 Allgemeine Flughafendaten
| Bezeichnung des Flughafens | Hypothetischer Flughafen | |
| Koordinatensystem | UTM, Zone 15, Referenz WGS-84 | |
| Flugplatzbezugspunkt, ARP | 3.600.00 m E | 6.300.00 m N |
| Mittelpunk Start-/Landebahn 09L-27R | ||
| Höhe ARP | 120 m / | |
| Durchschnittliche Lufttemperatur ARP * | 12,0 °C | |
| Durchschnittliche relative Luftfeuchtigkeit am ARP * | 60 % | |
| Durschn. Windgeschwindigkeit und Windrichtung * | 5 kt | 270 Grad |
| Quelle der topografischen Daten | Unbekannt | |
| *) Für jedes interessierende Zeitintervall (Tageszeit, Jahrszeit usw.) zu wiederholen. | ||
A2 Bezeichnung der Start- bzw. Landebahn
| Bezeichnung der Start- bzw. Landebahn | 09L | |
| Anfangspunkt S/L-Bahn | 3.599.000 m E | 6.302.000 m N |
| Endpunkt S/L-Bahn | 3.603.000 m E | 6.302.000 m N |
| Start-of-Roll-Punkt | 3.599.000 m E | 6.302.000 m N |
| Landeschwelle | 3.599.700 m E | 6.302.000 m N |
| Höhe Anfang S/L-Bahn | 110 m | |
| Mittlere Bahnneigung (Gradient) | 0,001 | |
Handelt es sich um versetzte Landeschwellen, kann die Beschreibung der Start-/Landebahn wiederholt werden; alternativ besteht die Möglichkeit, Erläuterungen zu den versetzten Schwellen in den Abschnitt "Beschreibung des Kurses über Grund" aufzunehmen.
A3 Beschreibung des Kurses über Grund
Liegen keine Radardaten vor, so werden für die Beschreibung des Kurses über Grund die folgenden Angaben benötigt.
| Strecke Nr. | 001 | |||||
| Streckenbezeichnung | Dep 01-09L | |||||
| Ab S/L-Bahn | 09L | |||||
| Streckentyp | Abflug | |||||
| Länge der Versetzung gegenüber Start-of-Roll-Punkt | 0 m | |||||
| Anzahl Unterstrecken | 7 | |||||
| Beschreibung Kernstrecke | ||||||
| Segment Nr. | Geradlinig [m] | Gekrümmt | Standardabweichung für seitliche Streuung am Segmentende [m] | |||
| L/R | Steuerkursänderung [°] | Radius [m] | ||||
| 1 | 10.000 | 2.000 | ||||
| 3 | R | 90,00 | 3.000 | 2.500 | ||
| 4 | 20.000 | 3.000 | ||||
| Strecke Nr. | 002 | |||||
| Streckenbezeichnung | App 01-09L - Disp 300 | |||||
| Ab S/L-Bahn | 09L | |||||
| Streckentyp | Anflug | |||||
| Länge der Versetzung gegenüber Landeschwelle | 300 m | |||||
| Anzahl Unterstrecken | 1 | |||||
| Beschreibung Kernstrecke | ||||||
| Segment Nr. | Geradlinig [m] | Gekrümmt | Standardabweichung für seitliche Streuung am Segmentende [m] | |||
| L/R | Steuerkursänderung [°] | Radius [m] | ||||
| 1 | 30.000 | 0 | ||||
| Angaben zur Anflugstrecke | ||||||
| Gleitwinkel für Anflugstrecken | 2,7° | |||||
| Flughöhe bei Empfang der Gleitflugvorgabe | 4.000 ft | |||||
A4 Beschreibung Flugverkehr
| Bezugszeitrahmen | 366 d | = 8.784 h |
| (1.1.2014 bis 31.12.2014) | ||
| Tageszeitraum I | Von 7 bis 19 Uhr | = 12 h |
| Tageszeitraum II | Von 19 bis 23 Uhr | = 4 h |
| Tageszeitraum III | Von 23 bis 7 Uhr | = 8 h |
| DATENBLATT FLUGVERKEHRSBESCHREIBUNG - BEWEGUNGEN PRO STRECKE | ||||
| Flugweg Nr. | 001 | |||
| Streckenbezeichnung | Dep 01 - 09L | |||
| Flugzeugbezeichnung | Bewegungen im Zeitraum | |||
| I | II | III | ||
| A/C 1, Dep.1 | 20.000 | 4.000 | 1.000 | |
| A/C 2, Dep.4 | 10.000 | 5.000 | 500 | |
| A/C4, Dep.3 | 2.000 | 300 | 0 | |
| Flugweg Nr. | 002 | |||
| Streckenbezeichnung | Dep 01 - 09L - Disp 300 | |||
| Flugzeugbezeichnung | Bewegungen im Zeitraum | |||
| I | II | III | ||
| A/C 1, App.1 | 18.000 | 2.000 | 5.000 | |
| A/C 2, App.1 | 10.000 | 3.000 | 2.500 | |
| A/C 4, App.1 | 1.300 | 0 | 1.000 | |
A5 Datenblatt Flugverfahren
Beispiel:
Boeing 727-200 Kapitel 3 entsprechend der Ableitung aus den Radardaten mit Hilfe der Hinweise in Abschnitt 2.7.9 des Haupttextes.
| Flugzeugbezeichnung | B727C3 | ||||
| NPD-ID-Kennung laut ANP-Datenbank | JT8E5 | ||||
| Anzahl Triebwerke | 3 | ||||
| Betriebsweise | Abflug | ||||
| Tatsächliche Flugzeugmasse [t] | 71,5 | ||||
| Gegenwind [m/s] | 5 | ||||
| Temperatur [°C] | 20 | ||||
| Flugplatzhöhe NN [m] | 83 | ||||
| Segment Nr. | Abstand zum Bezugspunkt (RP) 1 [m] | Höhe [m] | Geschwindigkeit über Grund [m/s] | Triebwerksleistung 2 | |
| 1 | 0 | 0 | 0 | 14.568 | |
| 2 | 2.5000 | 0 | 83 | 13.335 | |
| 3 | 3.000 | 117 | 88 | 13.120 | |
| 4 | 4.000 | 279 | 90 | 13.134 | |
| 5 | 4.500 | 356 | 90 | 13.147 | |
| 6 | 5.000 | 431 | 90 | 13.076 | |
| 7 | 6.000 | 543 | 90 | 13.021 | |
| 8 | 7.000 | 632 | 93 | 12.454 | |
| 9 | 8.000 | 715 | 95 | 10.837 | |
| 10 | 10.000 | 866 | 97 | 10.405 | |
| 11 | 12.000 | 990 | 102 | 10.460 | |
| 12 | 14.000 | 1.122 | 111 | 10.485 | |
| 13 | 16.000 | 1.272 | 119 | 10.637 | |
| 14 | 18.000 | 1.425 | 125 | 10.877 | |
| 15 | 20.000 | 1.581 | 130 | 10.870 | |
| 16 | 25.000 | 1.946 | 134 | 10.842 | |
| 17 | 30.000 | 2.242 | 142 | 10.763 | |
| 1) Der Bezugspunk (RP) ist bei Abflügen der Start-of-Roll-Punkt und bei Anflügen die Landeschwelle.
2) Die Einheiten entsprechen den Einheiten laut ANP-Datenbank. | |||||
Beispiel für ein Flugverfahrensprofil anhand der in der ANP-Datenbank abgelegten A/C-Daten:
| Flugzeugbezeichnung laut ANP-Datenbank | B727C3 | ||||
| NPD-ID-Kennung laut ANP-Datenbank | JT8E5 | ||||
| Anzahl Triebwerke | 3 | ||||
| Betriebsweise | Abflug | ||||
| Tatsächliche Flugzeugmasse [t] | 71,5 | ||||
| Gegenwind [m/s] | 5 | ||||
| Temperatur [°C] | 15 | ||||
| Flugplatzhöhe NN [m] | 100 | ||||
| Segment Nr. | Modus | Ziel | Klappen | Triebwerksleistung | |
| 1 | Start | 5 | Starten | ||
| 2 | Anfangssteigflug | Flughöhe 1.500 ft | 5 | Starten | |
| 3 | Klappen einfahren | 210 kt angezeigt (IAS)
Steigrate ROC 750 ftmin | 0 | Max. Steigen | |
| 4 | Beschleunigen | 250 kt angezeigt (IAS)
Steigrate 1.500 ft/min | 0 | Max. Steigen | |
| 5 | Steigflug | 10.000 ft | 0 | Max. Steigen | |
| Flugleistungsberechnung | Anlage B |
Begriffe und Symbole
Die in Anlage B verwendeten Bezeichnungen und Symbole entsprechen dem herkömmlichen Sprachgebrauch der Ingenieure im Bereich der Flugleistungsberechnung. Einige grundlegende Begriffe werden im Folgenden im Interesse fachfremder Anwender näher umrissen. Um Widersprüche mit dem Haupttext möglichst gering zu halten, sind die Symbole in dieser Anlage meist separat definiert. Im Haupttext angegebene Größen haben hier die gleichen Symbole; einige wenige Größe werden abweichend verwendet und sind mit einem Sternchen (*) versehen. Gelegentlich stehen US- Einheiten und SI-Einheiten nebeneinander; auch das geschieht im Interesse der Konventionen, die den Anwendern verschiedener Disziplinen geläufig sind.
Begriffe
| Break-Point | "Break-Point", siehe Flat-Rating |
| Berichtigte Fluggeschwindigkeit (CAS) | (auch bezeichnet als kalibrierte, äquivalente oder korrigiert angezeigte Fluggeschwindigkeit oder Gerätegeschwindigkeit). Die Geschwindigkeit des Luftfahrzeugs bezogen auf die umgebende Luft entsprechend der Anzeige eines kalibrierten Bordinstruments. Die Eigengeschwindigkeit (wahre Fluggeschwindigkeit) ist normalerweise höher und kann bei bekannter Luftdichte anhand der korrigiert angezeigten Fluggeschwindigkeit berechnet werden. |
| Korrigierter Nettoschub | Der Nettoschub ist die Antriebskraft, die ein Triebwerk auf die Flugzeugzelle ausübt. Bei einer gegebenen Einstellung der Leistung (EPR oder N1) nimmt diese Kraft bei wachsender Höhe mit der Luftdichte ab; der korrigierte Nettoschub ist der Schub auf Höhe des Meeresspiegels. |
| Flat-Rating | Bei bestimmten hohen Baugruppentemperaturen kommt es mit ansteigender Umgebungslufttemperatur zu einem Abfall des Triebwerksschubs - und umgekehrt. Das bedeutet, es besteht eine kritische Lufttemperatur, bei deren Überschreiten der Nennschub nicht mehr erreicht werden kann. Bei neuesten Triebwerken wird das als "Flat- Rated Temperature" bezeichnet, da bei niedrigeren Lufttemperaturen der Schub im Interesse einer maximalen Nutzungsdauer automatisch auf Nennschub begrenzt wird. Der Schub fällt bei Temperaturen oberhalb dieser Grenztemperatur ohnehin ab. Diese Leistungsgrenze wird oft auch als "Break-Point" oder "Break-Temperatur" bezeichnet. |
| Geschwindigkeit | Betrag des Geschwindigkeitsvektors (bezogen auf das Flugplatzkoordinatensystem). |
| Nennschub | Die Nutzungsdauer eines Flugzeugtriebwerks hängt stark von den Betriebstemperaturen seiner Komponenten ab. Je höher die erzeugte Leistung bzw. der erzeugte Schub, desto höher die Temperaturen und desto kürzer die Lebensdauer. Um die Anforderungen an Leistung und Lebensdauer gleichermaßen zu berücksichtigen, haben leistungsangepasste ("flat-rated") Triebwerke spezielle Nennwerte (Schub-Ratings) für Abheben, Steigflug und Reiseflug, mit denen maximal zulässige Leistungswerte für den Normalbetrieb festgelegt sind. |
| Schubeinstellungsparameter | Der Pilot kann keinen speziellen Triebwerksschub anwählen, sondern wählt stattdessen eine geeignete Einstellung für diesen Parameter, der im Cockpit angezeigt wird, üblicherweise das Triebwerksdruckverhältnis (EPR) oder die Drehzahl (N1) des Niederdruckrotors (oder Fans). |
Symbole
Kenngrößen sind dimensionslos, soweit nicht anders angegeben. Symbole und Abkürzungen, die in der Liste fehlen, werden nur sporadisch gebraucht und an entsprechender Stelle im Text definiert. Die Indizes 1 und 2 bezeichnen die am Anfang bzw. Ende eines Segments vorliegenden Bedingungen. Überstriche bezeichnen Segmentmittelwerte, d. h. dem Durchschnitt von Start- und Endwerten.
| a | Mittlere Beschleunigung, ft/s2 |
| amax | Maximal verfügbare Beschleunigung, ft/s2 |
| A, B, C, D | Klappenbeiwerte |
| E, F, GA,B, H | Triebwerksschubbeiwerte |
| Fn | Nettoschub je Triebwerk, lbf |
| Fn/δ | Korrigierter Nettoschub je Triebwerk, lbf |
| G | Steiggradient |
| G' | Steiggradient bei Triebwerksausfall |
| GR | Mittlerer Start-/Landebahngradient, positiv bei Steigung |
| g | Schwerebeschleunigung, ft/s2 |
| ISA | Internationale Standardatmosphäre |
| N * | Anzahl der Schub erzeugenden Triebwerke |
| R | Gleitzahl CD/CL |
| ROC | Segment-Steigrate (ft/min) |
| s | Zurückgelegter Weg auf dem Flugweg, ft |
| sTO8 | Startstrecke bei Gegenwind von 8 kt, ft |
| sTOG | Nach w und GR korrigierte Startstrecke, ft |
| sTOw | Startstrecke bei Gegenwind w, ft |
| T | Lufttemperatur, °C |
| TB | Break-Point-Temperatur, °C |
| V | Geschwindigkeit über Grund, kt |
| VC | Berichtigte Fluggeschwindigkeit, kt |
| VT | Wahre Fluggeschwindigkeit, kt |
| W | Flugzeuggewicht, lb |
| w | Gegenwindgeschwindigkeit, kt |
| Δs | Auf den Flugweg projizierte Segmentlänge in stiller Luft, ft |
| Δsw | Gegenwindberichtigte bodenprojizierte Segmentlänge, ft |
| δ | p/po, Verhältnis Außenluftdruck am Flugzeug zum Normalluftdruck auf Meereshöhe: po = 101,325 kPa (bzw. 1.013,25 mb) |
| ε | Querneigungswinkel, Radiant |
| γ | Steigwinkel/Sinkwinkel, Radiant |
| ϑ | (T + 273,15)/(T0 + 273,15) Verhältnis Lufttemperatur in der Höhe zur Standardlufttemperatur auf Meereshöhe: T0 = 15,0 °C |
| σ * | ρ/ρ0 = Verhältnis Luftdichte in der Höhe zu NN-Wert (auch σ = δ/ϑ) |
B1 Einführung
Flugbahnsynthese
In dieser Anlage werden Empfehlungen für Verfahren zur Berechnung des Flugprofils eines Flugzeugs anhand spezifischer aerodynamischer und triebwerksbezogener Parameter, des Flugzeuggewichts, der atmosphärischen Bedingungen, des Kurses über Grund und des Betriebsverfahrens (Flugkonfiguration, Leistungseinstellung, Vorwärtsgeschwindigkeit, Vertikalgeschwindigkeit usw.). Das Betriebsverfahren wird als Satz von Verfahrensschritten beschrieben, mit denen vorgeschrieben wird, wie das Profil zu fliegen ist.
Das Flugprofil für Start oder Anflug wird von einer Reihe geradliniger Segmente dargestellt, deren Endpunkte als Profilpunkte bezeichnet werden. Die Berechnung des Flugprofils erfolgt mit aerodynamischen und schubkraftbezogenen Gleichungen, die zahlreiche Koeffizienten und Konstanten enthalten, die für die spezielle Kombination von Flugzeugzelle und Triebwerk bekannt sein müssen. Dieser Berechnungsprozess wird im Text als Synthese der Flugbahn bezeichnet.
Neben den Leistungsparametern des Luftfahrzeugs, die aus der ANP-Datenbank bezogen werden können, sind für diese Gleichungen folgende Angaben erforderlich: 1) Flugzeug-Bruttogewicht, 2) Anzahl der Triebwerke, 3) Lufttemperatur, 4) Höhe der Start-/Landebahn über NN und 5) die Verfahrensschritte (ausgedrückt als Leistungseinstellungen, Klappenstellung, Fluggeschwindigkeit und - während der Beschleunigung - durchschnittliche Steig-/ Sinkgeschwindigkeit) für jedes Segment während Start und Anflug. Jedes Segment wird dann eingeordnet als Startlauf, Abheben oder Landen, Steigflug mit konstanter Geschwindigkeit, Leistungsdrosselung, Steigen mit Beschleunigung mit oder ohne Klappeneinziehen, Sinken mit oder ohne Abbremsung und/oder Klappenanstellung, oder Endanflug. Das Flugprofil wird Schritt für Schritt aufgebaut, wobei die Anfangsparameter eines jeden Segments identisch mit den Endparametern des vorhergehenden Segments sind.
Die aerodynamischen Leistungsparameter in der ANP-Datenbank sollen die tatsächliche Flugbahn eines Flugzeugs für die angegebenen Referenzbedingungen mit ausreichender Genauigkeit darstellen (siehe Abschnitt 2.7.6 im Haupttext). Die Eignung der aerodynamischen Parameter und Triebwerksbeiwerte für Lufttemperaturen bis 43 °C, Flugplatzhöhen bis 4.000 ft und über einen in der ANP-Datenbank angegebenen Gewichtsbereich ist nachgewiesen. Die Gleichungen gestatten demnach die Berechnung von Flugbahnen für andere Bedingungen - d. h. Flugzeuggewicht, Windgeschwindigkeit, Lufttemperatur und Flugbahnhöhe (Luftdruck) außerhalb des Referenzbereichs - in der Regel mit ausreichender Genauigkeit für die Berechnung durchschnittlicher Schallpegelkonturen in der Umgebung eines Flughafens.
Abschnitt B-4 erläutert, wie die Kurvenflugeffekte beim Starten berücksichtigt werden. Damit lässt sich die Querneigung bei der Berechnung der seitlichen Richtwirkungseffekte (Effekte der Triebwerksanbringung) einbeziehen. Beim Kurvenflug werden abhängig von Kurvenradius und Flugzeuggeschwindigkeit in der Regel auch die Steiggradienten reduziert. (Die Kurvenflugeffekte im Landeanflug sind komplexer und werden erst einmal ausgespart. Das wirkt sich jedoch auf die Lärmkonturen kaum aus.)
In den Abschnitten B-5 bis B-9 werden die empfohlene Methodik für die Erstellung von Abflugprofilen anhand von ANP-Beiwerten und Verfahrensschritten beschrieben.
Die Abschnitte B-10 und B-11 haben die verwendete Methodik für die Erstellung von Anflugprofilen anhand von ANP-Beiwerten und Verfahrensschritten zum Gegenstand.
Abschnitt B-12 enthält durchgerechnete Beispiele.
Für die Berechnung des Nettoschubs von Düsentriebwerken bzw. Propellern sind separate Gleichungssätze vorgesehen. Sofern nicht anders angemerkt, gelten die Gleichungen für die aerodynamische Leistung eines Flugzeugs für düsen- und propellergetriebene Flugzeuge gleichermaßen.
Mathematische Symbole sind am Anfang dieser Anlage und/oder beim ersten Auftreten im Text definiert. In allen Gleichungen müssen die Einheiten der Beiwerte, Koeffizienten und Konstanten natürlich mit den Einheiten der entsprechenden Parameter und Variablen übereinstimmen. Um Übereinstimmung mit den ANP-Datenbanken zu gewährleisten, wird in dieser Anlage den im Bereich der Flugzeugleistungsrechnung üblichen Konventionen gefolgt: Angabe der Strecken und Höhen in Fuß (ft), Geschwindigkeit in Knoten (kt), Masse in Pound (lb), Kraft in Pound-force (korrigierter Nettoschub für hohe Temperaturen) und so weiter - auch wenn bestimmte Maße (z.B. Atmosphäre) in SI- Einheiten ausgedrückt werden. Werden bei der Modellierung abweichende Einheiten verwendet, sollte sehr sorgfältig darauf geachtet werden, dass bei Übernahme der Gleichungen entsprechende Umrechnungsfaktoren zur Anwendung kommen.
Flugbahnanalyse
In einigen Modellierungsprogrammen werden die Flugbahninformationen nicht als Verfahrensschritte dargestellt, sondern als Positions- und Zeitkoordinaten, die gewöhnlich über die Analyse von Radardaten ermittelt werden. Dies wird in Abschnitt 2.7.7 des Haupttextes erörtert. In diesem Fall werden die hier vorgestellten Gleichungen "umgekehrt" verwendet, d. h. die Schubparameter der Triebwerke werden aus der Bewegung des Luftfahrzeugs abgeleitet und nicht umgekehrt. Nachdem die Flugbahndaten gemittelt und auf Segmentform reduziert worden sind und jedes Segment nach Steigen oder Sinken, Beschleunigen oder Abbremsen sowie Schub- und Klappenveränderungen eingeordnet ist, handelt es sich im Allgemeinen um einen relativ geradlinigen Vorgang, anders als bei der Synthese, wo oftmals iterative Prozesse ablaufen.
B2 Triebwerksschub
Die von jedem Triebwerk erzeugte Antriebskraft ist eine der fünf Größen, die am Ende jedes einzelnen Flugbahnsegments festzulegen ist (neben Flughöhe über Grund, Geschwindigkeit, Leistungseinstellung und Querneigung). Der Nettoschub stellt diejenige Komponente des Bruttoschubs eines Triebwerks dar, die für den Antrieb zur Verfügung steht. Bei aerodynamischen und akustischen Berechnungen ist der Nettoschub auf Normalluftdruck auf Meereshöhe bezogen. Dies wird als korrigierter Nettoschub Fn/δ bezeichnet.
Das ist entweder der Nettoschub, der verfügbar ist, wenn mit einem vorgegebenen Schub-Rating gearbeitet wird, oder der Nettoschub, der sich ergibt, wenn der Schubeinstellungsparameter auf einen bestimmten Wert gesetzt wird. Für ein Turbojet- oder Turbofantriebwerk, das mit einem spezifischen Schub-Rating arbeitet, ergibt sich der korrigierte Nettoschub aus der Gleichung
| Fn/δ = E + F · Vc + GA· h + GB· h2 + H · T | (B-1) |
wobei Folgendes gilt:
| Fn | Nettoschub je Triebwerk, lbf, |
| δ | Verhältnis Außenluftdruck am Flugzeug zum Normalluftdruck auf Meereshöhe, d. h. zu 101,325 kPa (oder 1.013,25 mb) [ Ref. 1], |
| Fn/δ | korrigierter Nettoschub je Triebwerk, lbf, |
| VC | berichtigte Fluggeschwindigkeit, kt, |
| T | Außenlufttemperatur, in der das Flugzeug sich bewegt (°C), und |
| E, F, GA, GB, H | Schubkonstanten oder Schubbeiwerte für Temperaturen unterhalb der Flat-Rating-Temperatur des Triebwerks bei verwendetem Schub-Rating (am aktuellen Segment der Flugbahn für Start/Aufstieg bzw. Anflug), lb.s/ft, lb/ft, lb/ft2, lb/°C. Können aus der ANP-Datenbank bezogen werden. |
In der ANP-Datenbank werden auch Daten bereitgestellt, die die Berechnung des nicht begrenzten Schubs in Abhängigkeit von einem Schubeinstellungsparameter ermöglichen. Das wird von einigen Herstellern als Triebwerksdruckverhältnis EPR (Engine Pressure Ratio), von anderen als "Low-Pressure Rotor Speed" oder Fandrehzahl N1 bezeichnet. Wenn dieser Parameter das Druckverhältnis EPR ist, wird Gleichung B-1 ersetzt durch
| Fn/δ = E + F · VC + GA · h + GB · h2 + H · T + K1 · EPR + K2 · EPR2 | (B-2) |
wobei K1 und K2 Koeffizienten aus der ANP-Datenbank sind, die den korrigierten Nettoschub und das Triebwerksdruckverhältnis im Bereich des für die vorgegebene Machzahl des Flugzeugs interessierenden Triebwerksdruckverhältnisses verknüpfen.
Wenn das Flugpersonal die Triebwerkdrehzahl N1 als Schubeinstellungsparameter verwendet, sieht die verallgemeinerte Schubgleichung wie folgt aus
|
| (B-3) |
wobei Folgendes gilt:
| N1 | Drehzahl von Niederdruckkompressor- (oder Fan-) und Niederdruckturbinenstufe des Triebwerks, %, |
| ϑ | = (T + 273)/288,15, Verhältnis der absoluten Gesamttemperatur am Triebwerkseinlass zur absoluten Standardlufttemperatur auf Meereshöhe [Ref. 1], |
| N1/√ϑ | korrigierte Niederdruckrotordrehzahl, %; und |
| K3, K4 | Konstanten, abgeleitet aus Triebwerksdaten, die die interessierende Drehzahl N1 umfassen. |
An dieser Stelle ist anzumerken, dass E, F, GA, GB und H in den Gleichungen B-2 und B-3 beim betreffenden Flugzeug andere Werte als in Gleichung B-1 annehmen können.
Nicht jeder Term der Gleichung ist in jedem Falle erheblich. So kann sich beispielsweise für Flat-Rated-Triebwerke der Temperatur-Term erübrigen, wenn die Lufttemperatur unterhalb des Break-Points (typischerweise 30 °C) liegt. Bei Triebwerken ohne Flat-Rating ist bei der Schubbemessung die Umgebungstemperatur zu berücksichtigen. Oberhalb der Flat-Rating-Temperatur des Triebwerks müssen für die Bestimmung des verfügbaren Schubs andere Koeffizienten (E, F, GA, GB und H)high verwendet werden. Die normale Vorgehensweise wäre dann, dass Fn/δ mit Hilfe sowohl unterer als auch oberer Temperaturbeiwerte berechnet wird und der höhere Schubwert für Temperaturen unter der Flat-Rating-Temperatur und der untere berechnete Schubwert für Temperaturen über der Flat-Rating-Temperatur verwendet wird.
Soweit nur Schubbeiwerte für den unteren Temperaturbereich vorliegen, kann das folgende Verhältnis Verwendung finden:
| (Fn/δ)high = F · VC + (E + H · TB)·(1 - 0,006 · T)/(1 - 0,006 · TB) | (B-4) |
wobei Folgendes gilt:
| (Fn/δ)high | korrigierter Nettoschub für hohe Temperaturen (lbf), |
| TB | Break-Point-Temperatur (falls kein definitiver Wert vorhanden, ist ein Standardwert von 30 °C anzusetzen). |
Die ANP-Datenbank enthält Werte für die Konstanten und Koeffizienten (Beiwerte) der Gleichungen B-1 bis B-4.
Für propellergetriebene Flugzeuge sollte der korrigierte Nettoschub des jeweiligen Triebwerks aus Diagrammen abgelesen oder mit folgender Gleichung berechnet werden:
| Fn/δ = (326 · η · Pp/VT)/δ | (B-5) |
wobei Folgendes gilt:
| η | Propellerwirkungsgrad einer gegebenen Art der Propelleranbringung und in Abhängigkeit von Propellerdrehzahl und Fluggeschwindigkeit des Flugzeugs, |
| VT | wahre Fluggeschwindigkeit, kt, |
| Pp | Nettoantriebskraft für die gegebene Flugbedingung, z.B. maximale Startleistung oder maximale Steigleistung, hp. |
Die Parameter in Gleichung B-5 werden in der ANP-Datenbank für die Einstellungen des maximalen Startschubs und des maximalen Steigschubs bereitgestellt.
Die wahre Fluggeschwindigkeit VT wird anhand der berichtigten Fluggeschwindigkeit VC nach folgender Beziehung schätzungsweise ermittelt:
| VT = VC/√σ | (B-6) |
wobei σ: Verhältnis Luftdichte am Flugzeug zum Wert auf Höhe über NN.
Hinweise zum Arbeiten mit vermindertem Startschub
Es kommt nicht selten vor, dass das Startgewicht eines Luftfahrzeugs geringer ist als das zulässige Startgewicht und/oder die verfügbare Startbahnlänge die für den maximalen Startschub erforderliche Mindestlänge überschreitet. In solchen Fällen hat es sich in der Praxis durchgesetzt, dass der Triebwerksschub im Interesse einer längeren Lebensdauer der Triebwerke und teilweise auch aus Lärmschutzgründen auf Werte unter Maximum reduziert wird. Der Triebwerksschub kann nur soweit herabgesetzt werden, wie dies die Sicherheit nicht gefährdet. Das von Luftverkehrsgesellschaften verwendete Berechnungsverfahren zur Bestimmung des Schubreduzierungsbetrags ist dementsprechend reguliert: das Verfahren ist komplex und berücksichtigt zahlreiche Faktoren wie Startgewicht, Außenlufttemperatur, gemeldete Startbahnstrecken, Startbahnhöhe und Kriterien der Hindernisfreiheit. Deshalb variiert die Schubreduzierung von Flug zu Flug.
Da die Auswirkungen auf die Lärmkonturen im Startbereich enorm sein können, sollten die Schubreduzierungen bei der Modellierung angemessen berücksichtigt werden, wozu im Interesse bestmöglicher Vorkehrungen praktischer Rat von den Luftverkehrsgesellschaften eingeholt werden sollte.
Falls eine praktische Beratung nicht möglich ist, ist es auf jeden Fall ratsam, solche Einrechnungen auf alternative Weise vorzunehmen. Eine direkte Übernahme der betriebstechnischen Berechnungen in die Lärmmodellierung ist unpraktisch und wäre angesichts der üblichen Vereinfachungen und Näherungen, die zur Berechnung langfristiger durchschnittlicher Schallpegel vorgenommen werden, auch nicht zweckdienlich. Die folgenden Hinweise bieten eine praktikable Alternative. Da auf diesem Gebiet derzeit umfangreiche Forschungsarbeiten laufen, bleiben Änderungen vorbehalten.
Wie die Analyse der Daten von Flugdatenschreibern gezeigt hat, ist der Grad der Schubreduzierung stark an das Verhältnis des tatsächlichen Startgewichts zum zulässigen Startgewicht (RTOW) geknüpft, bis hin zu einem festen unteren Grenzwert 1; d. h.
| Fn/δ = (Fn/δ)max · W/WRTOW | (B-7) |
wobei: (Fn/δ)max maximaler Nennschub, W tatsächliches Bruttostartgewicht und WRTOW zulässiges Startgewicht.
Das zulässige Startgewicht (RTOW) ist das zulässige Startgewicht, das unter Einhaltung der Startstreckenlänge sowie Triebwerksausfall- und Hindernisanforderungen gefahrlos eingesetzt werden kann. Das RTOW ist abhängig von verfügbarer Startbahnlänge, Flugplatzhöhe, Temperatur, Gegenwind und Klappenwinkel. Diese Informationen können bei den Luftverkehrsgesellschaften eingeholt werden und dürften einfacher erhältlich sein als Angaben über tatsächliche Schubreduzierungen. Das RTOW kann alternativ dazu mit Daten aus Flughandbüchern berechnet werden.
Reduzierter Steigschub
Wenn Luftverkehrsgesellschaften mit reduziertem Startschub arbeiten, setzen sie oft, aber nicht immer, den Steigschub im Verhältnis zum Maximum herunter 2. Damit wird Situationen vorgebeugt, in denen am Ende des mit Startschub vorgenommenen Anfangssteigflugs die Leistung erhöht werden muss, statt dass sie zurückgenommen wird. Hier lässt sich jedoch eine gemeinsame Basis schwieriger formulieren. Einige Gesellschaften verwenden unterhalb des maximalen Steigschubs feste Stufen, die manchmal als Steigstufe 1 und Steigstufe 2 bezeichnet werden und den Steigschub typischerweise um 10 % bzw. 20 % gegenüber dem Maximum reduzieren. Es wird empfohlen, bei Verwendung eines reduzierten Startschubs auch die Steigschubwerte um 10 % zu reduzieren.
B3 Vertikalprofile von Lufttemperatur, Luftdruck, Luftdichte und Windgeschwindigkeit
Im Rahmen dieses Dokuments wird davon ausgegangen, dass die höhenabhängigen Temperatur-, Druck- und Dichteschwankungen entsprechend der internationalen Standardatmosphäre auf die Höhe über Normalnull bezogen sind. Die nachstehend beschriebenen Methoden sind für Flugplatzhöhen bis zu 4.000 ft über Meereshöhe und für Lufttemperaturen bis zu 43 °C (109 °F) bestätigt.
Die mittlere Windgeschwindigkeit ist in Wirklichkeit zwar höhen- und zeitabhängig, aber für die Modellierung von Lärmkonturen ist eine Einrechnung dieser Variabilität in der Regel nicht praktikabel. Statt dessen beruhen die im Folgenden angegebenen Flugleistungsgleichungen auf der allgemeinen Annahme, dass das Flugzeug jederzeit direkt in einen (Standard-)Gegenwind von 8 kt hineinsteuert - unabhängig vom Kompasskurs (obwohl in Schallausbreitungsrechnungen kein expliziter Ansatz einer mittleren Windgeschwindigkeit erfolgt). Es werden Methoden zur Anpassung der Ergebnisse an andere Gegenwindgeschwindigkeiten angeboten.
B4 Kurvenflugeffekte
In den restlichen Abschnitten dieser Anlage werden die methodischen Ansätze zur Berechnung der erforderlichen Eigenschaften der Segmente, die die Profilpunkte s,z verbinden und die zweidimensionale Flugbahn in der vertikalen Ebene über dem Flugweg definieren. Die Reihenfolge der Segmente folgt der Bewegungsrichtung. Am Ende eines jeden Segments (bzw. am Anfang der Rollbewegung im Falle des ersten Segments einer Abflugsequenz), wo die Betriebsparameter und der nächste Verfahrensschritt festgelegt werden, müssen Steigwinkel und zurückgelegte Strecke bis zu dem Punkt, an dem die erforderliche Höhe und/oder Geschwindigkeit erreicht wird, berechnet werden.
Bei gerader Strecke wird hierzu ein einzelnes Profilsegment verwendet, dessen Geometrie dann direkt (teilweise aber auch mit iterativem Anteil) bestimmt werden kann. Falls jedoch eine Kurve beginnt oder endet oder sich der Radius bzw. die Richtung der Kurve ändert, bevor die geforderten Endbedingungen erreicht sind, wäre ein Einzelsegment unzureichend, da sich Auftrieb und Luftwiderstand des Luftfahrzeugs mit der Querneigung ändern. Zur Berücksichtigung der Kurveneffekte auf den Steigflug sind zur Umsetzung des Verfahrensschrittes zusätzliche Profilsegmente wie folgt erforderlich.
Die Konstruktion des Kurses über Grund ist in Abschnitt 2.7.13 des Haupttextes beschrieben. Dies geschieht unabhängig vom Flugprofil eines Luftfahrzeugs (wobei aber sorgfältig darauf zu achten ist, keine Kurven zu definieren, die unter normalen Betriebszwängen gar nicht geflogen werden könnten). Da jedoch Kurven einen Einfluss auf das Flugprofil - Flughöhe über Grund und Geschwindigkeit in Abhängigkeit von der zurückgelegten Strecke - nehmen, lässt sich das Flugprofil nicht unabhängig vom Flugweg bestimmen.
Um in einem Kurvenflug die Geschwindigkeit zu halten, muss der aerodynamische Auftrieb des Flügels so erhöht werden, dass Fliehkraft und Flugzeuggewicht ausgeglichen sind. Das erhöht jedoch den Widerstand und demzufolge den erforderlichen Antriebsschub. Die Effekte des Kurvenflugs werden in den Gleichungen der Leistungsrechnung in Abhängigkeit vom Querneigungswinkel ε ausgedrückt, der für ein Luftfahrzeug, das im Horizontalflug mit konstanter Geschwindigkeit auf einer kreisförmigen Kurvenbahn fliegt, wie folgt gegeben ist:
|
| (B-8) |
wobei
V Geschwindigkeit über Grund, kt,
r Kurvenradius, ft,
g ist die Schwerebeschleunigung, ft/s2.
Für alle Kurven wird ein konstanter Radius angenommen, während Effekte zweiter Ordnung aus nichthorizontalen Flugbahnen außer Acht gelassen werden; die Querneigungswinkel beruhen ausschließlich auf dem Kurvenradius r des Kurses über Grund.
Zur Umsetzung eines Verfahrensschritts wird mit Hilfe des am Anfangspunkt bestehenden Querneigungswinkels ε - wie in Gleichung B-8 für den Streckensegmentradius r definiert - ein vorläufiges Profilsegment berechnet. Falls die berechnete Länge des vorläufigen Segments weder den Anfangspunkt noch den Endpunkt einer Flugkurve kreuzt, wird das vorläufige Segment bestätigt und die Aufmerksamkeit wendet sich dem nächsten Schritt zu.
Falls aber das vorläufige Segment einen oder mehrere Start- oder Endpunkte von Kurven kreuzt (mit Änderung von ε) 3, werden die Flugparameter am ersten entsprechenden Punkt per Interpolation geschätzt (siehe Abschnitt 2.7.13) und gemeinsam mit dessen Koordinaten als Endpunktwerte abgespeichert und das Segment entsprechend abgeschnitten. Der zweite Teil des Verfahrensschritts beginnt dann am besagten Punkt - wobei vorläufig wieder davon ausgegangen wird, dass dieser Teilschritt mit den gleichen Endbedingungen, aber mit neuem Anfangspunkt und neuem Querneigungswinkel, in einem einzigen Segment abgeschlossen werden kann. Falls dieses zweite Segment auf eine weitere Änderung des Radius bzw. der Richtung der Kurve stößt, ist ein drittes Segment nötig - und so weiter bis zum Erreichen der Endbedingungen.
Näherungsmethode
Es wird deutlich, dass eine vollständige Berücksichtigung der Kurvenflugeffekte gemäß obiger Beschreibung ein rechnerisch hochkomplexer Vorgang ist, da das Steigprofil eines Luftfahrzeugs für jeden von ihm überflogenen Flugweg separat berechnet werden muss. Da kurvenflugbedingte Änderungen des Vertikalprofils in der Regel einen deutlich geringeren Einfluss auf die Konturen haben als Änderungen des Querneigungswinkels, verzichten einige Anwender zur Umgehung dieser Komplexität - wenn auch auf Kosten der Präzision - auf die Profilauswirkungen von Kurvenflügen, berücksichtigen bei der Berechnung der seitlichen Lärmabstrahlung jedoch den Querneigungswinkel (siehe Abschnitt 2.7.19). Bei dieser Approximation werden die Profilpunkte je Flug nur ein einziges Mal berechnet, und zwar unter Zugrundelegung eines geradlinigen Kurses über Grund (mit ε = 0).
B5 Startlaufstrecke
Der Startschub beschleunigt das Flugzeug auf der Startbahn bis zum Abheben. Die berichtigte Fluggeschwindigkeit wird dann für die gesamte Anfangsphase des Aufstiegs als konstant angenommen. Es wird angenommen, dass das Fahrwerk, sofern es einziehbar ist, kurz nach dem Abheben eingezogen wird.
Im Rahmen dieses Dokuments wird die tatsächliche Startlaufstrecke annäherungsweise durch eine äquivalente Startstrecke (mit Standard-Gegenwind von 8 kt), sTO8, bestimmt, die gemäß Abbildung B-1 definiert ist als die auf der Startbahn gelegene Entfernung ab dem Lösen der Bremse bis zu dem Punkt, an dem eine geradlinige Verlängerung der mit eingezogenem Fahrwerk vollzogenen anfänglichen Steigflugbahn die Startbahn schneidet.
Abbildung B-1 Äquivalente Startstrecke
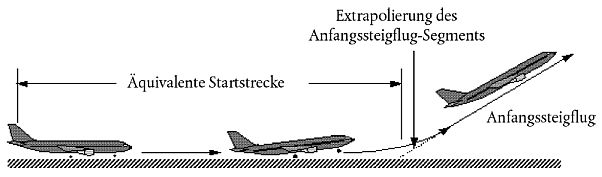
Für eine waagerechte Startbahn wird die äquivalente Startlaufstrecke sTO8 in Fuß anhand der folgenden Gleichung berechnet:
|
| (B-9) |
wobei Folgendes gilt:
B8 Beiwert mit Eignung für eine spezielle Kombination von Flugzeug/Klappenstellung für die ISA-Referenzbedingungen unter Einbeziehung von Gegenwind mit 8 kt, ft/lbf,
W Flugzeugbruttogewicht bei Lösen der Bremse, lbf,
N Anzahl Schub erzeugender Triebwerke.
Anmerkung: Da mit der Gleichung B-9 der unterschiedliche Schub in Abhängigkeit von Fluggeschwindigkeit und Startbahnhöhe berücksichtigt wird, hängt der Beiwert B8 für ein gegebenes Flugzeug allein von der Klappenstellung ab.
Bei Gegenwind, der nicht der Standardgeschwindigkeit von 8 kt entspricht, wird die Startlaufstrecke wie folgt korrigiert:
|
| (B-10) |
wobei Folgendes gilt:
| STow | Startlaufstrecke korrigiert in Bezug auf Gegenwind w, ft, |
| VC | (in dieser Gleichung) berichtigte Geschwindigkeit bei Startrotation, kt, |
| w | Gegenwind, kt. |
Die Startlaufstrecke wird wie folgt auch in Bezug auf den Startbahngradienten korrigiert:
|
| (B-11) |
wobei Folgendes gilt:
| STOG | in Bezug auf Gegenwind und Startbahngradient korrigierte Startlaufstrecke (ft), |
| α | mittlere Beschleunigung auf der Startbahn, gleich (VC - √σ)2 / (2 ⋅ sTOw), ft/s2, |
| GR | Startbahngradient; positiv bei Steigung in Startrichtung. |
B6 Steigflug mit konstanter Geschwindigkeit
Dieser Segmenttyp wird durch die berichtigte Fluggeschwindigkeit des Flugzeugs, die Klappeneinstellung und durch die Flughöhe über Grund und den Querneigungswinkel am Segmentende im Zusammenspiel mit der Gegenwindgeschwindigkeit (Standardwert 8 kt) definiert. Wie bei jedem Segment sind die Parameter am Segmentanfang, darunter der korrigierte Nettoschub, identisch mit den Parametern vom Ende des vorhergehenden Segments - es kommen keine Unstetigkeiten vor (außer bei Klappenwinkel und Querneigungswinkel, für die in diesen Berechnungen sprunghafte Änderungen zulässig sind). Die Nettoschubwerte des Segmentendes werden zuerst mit der zutreffenden Gleichung aus B-1 bis B-5 berechnet. Der durchschnittliche geometrische Steigwinkel γ (siehe Abbildung B-1) ergibt sich dann durch
|
| (B-12) |
wobei gilt: die Überstriche bezeichnen Mittelsegmentwerte (= Durchschnitt aus Startpunkt- und Endpunktwerten - in der Regel Werte aus der Segmentmitte) und
| K | geschwindigkeitsabhängige Konstante, ist 1,01 bei VC ≤ 200 kt oder sonst 0,95. Diese Konstante berücksichtigt die Auswirkungen auf den Steiggradienten durch einen Aufstieg bei 8 Knoten Gegenwind und die immanente Beschleunigung bei einem Steigflug mit konstanter berichtigter Fluggeschwindigkeit (die Eigenfluggeschwindigkeit steigt mit höhenbedingt abnehmender Luftdichte), |
| R | Verhältnis von Widerstandsbeiwert zu Auftriebsbeiwert des Flugzeugs entsprechend der gegebenen Klappenstellung. Das Fahrwerk wird als eingefahren angenommen, |
| ε | Querneigungswinkel, Radiant. |
Der Steigwinkel wird um den Gegenwind w wie folgt korrigiert:
|
| (B-13) |
wobei: γw mittlerer gegenwindbereinigter Steigwinkel.
Die Wegstrecke, die das Flugzeug über Grund zurücklegt, Δs, während es in einem Winkel von γw von der Anfangshöhe h1 zu einer Endhöhe h2 aufsteigt, ergibt sich durch
|
| (B-14) |
In der Regel kommt der Steigflug mit konstanter Fluggeschwindigkeit in zwei getrennten Phasen eines Abflugprofils vor. Die erste Phase, die zuweilen als Anfangssteigflug bezeichnet wird, beginnt unmittelbar nach dem Abheben, wo aus Gründen der Sicherheit die Fluggeschwindigkeit des Flugzeugs mindestens der sicheren Steigfluggeschwindigkeit entsprechen muss. Dies ist eine vorgeschriebene Geschwindigkeit und muss bei Normalstart spätestens in einer Höhe von 35 ft über der Startbahn erreicht werden. Es ist jedoch allgemeine Praxis, im Anfangssteigflug eine Geschwindigkeit zu fliegen, die etwas höher, und zwar 10-20 kt höher, als die sichere Steigfluggeschwindigkeit ist, was für einen tendenziell besseren Steiggradienten in dieser Anfangsphase sorgt. Die zweite Phase beginnt nach dem Rückfahren der Klappe und der Anfangsbeschleunigung und wird als Steigflug bezeichnet.
Im Anfangssteigflug hängt die Fluggeschwindigkeit von der Stellung der Startklappen und vom Bruttogewicht des Flugzeugs ab. Die berichtigte Anfangssteiggeschwindigkeit VCTO wird in erster Näherung wie folgt berechnet:
| VCTO = C ⋅ √W | (B-15) |
Wobei C ein geeigneter Beiwert für die Klappeneinstellung (kt/√lbf) ist, der aus der ANP-Datenbank ausgelesen wird.
Beim Steigflug nach erfolgter Beschleunigung ist die berichtigte Fluggeschwindigkeit ein vom Anwender eingegebener Parameter.
B7 Schubrücknahme (Übergangssegment)
Der Schub wird an einem bestimmten Punkt nach dem Start reduziert bzw. gedrosselt (Cutback), um die Triebwerke zu schonen und oft auch um in bestimmten Gebieten den Lärmpegel zu reduzieren. Die Schubreduzierung erfolgt normalerweise entweder in einem mit konstanter Geschwindigkeit geflogenen Steigflugsegment (Abschnitt B6) oder in einem Beschleunigungssegment (Abschnitt B8). Da es sich um einen relativ kurzen Vorgang handelt, der in der Regel nur 3 bis 5 Sekunden dauert, wird die Schubrücknahme dadurch modelliert, dass dem Primärsegment ein "Übergangssegment" angefügt wird. Dies erfolgt gewöhnlich für eine horizontale Bodendistanz von 1.000 ft (305 m).
Betrag der Schubreduzierung
Im Normalbetrieb wird der Schub des Triebwerks auf die Einstellung für maximalen Steigschub abgesenkt. Anders als der Startschub kann der Steigschub unendlich gehalten werden, in der Praxis üblicherweise bis zum Erreichen der ersten Reiseflughöhe des Flugzeugs. Der maximale Steigschub bestimmt sich aus Gleichung B-1 mit Hilfe der vom Hersteller bereitgestellten maximalen Schubbeiwerte. Aus Gründen des Lärmschutzes kann jedoch eine zusätzliche Schubreduzierung erforderlich werden, die auch als "Deep Cutback" bezeichnet wird. Aus Sicherheitsgründen ist die maximale Schubreduzierung auf einen Betrag begrenzt 4, der sich aus der Flugzeugleistung und der Triebwerkzahl bestimmt.
Diese Untergrenze der Schubreduzierung wird manchmal auch als Engine-Out-Schubreduzierung bezeichnet:
|
| (B-16) |
wobei Folgendes gilt:
| δ2 | Druckverhältnis in Höhe h2, |
| G' | Steiggradient bei Triebwerksausfall in Prozent:
= 0 % für Flugzeuge mit ATR-Schubautomatik; sonst, = 1,2 % für Flugzeug mit 2 Triebwerken, = 1,5 % für Flugzeug mit 3 Triebwerken, = 1,7 % für Flugzeug mit 4 Triebwerken. |
Steigflugsegment mit konstanter Geschwindigkeit und Schubreduzierung
Der Gradient des Steigflugsegments wird mit Gleichung B-12 berechnet, wobei der Schub entweder nach B-1 mit Maximalsteigungsbeiwerten oder bei reduziertem Schub nach B-16 berechnet wird. Das Steigflugsegment wird anschließend in zwei Teilsegmente aufgeteilt, die den gleichen Steigwinkel aufweisen. Das ist in Abbildung B-2 illustriert.
Abbildung B-2 Steigflugsegment mit konstanter Geschwindigkeit und Schubreduzierung (Abbildung nicht maßstabsgetreu)
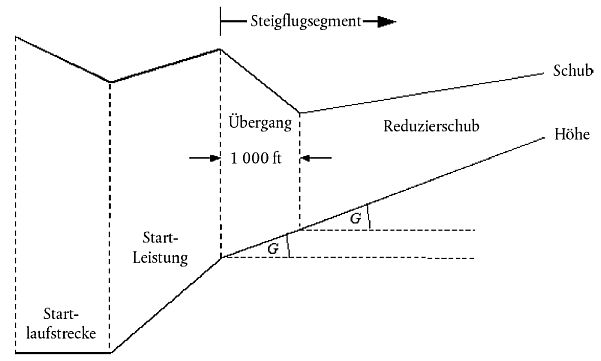
Dem ersten Teilsegment wird eine Strecke über Grund von 1.000 ft (304 m) zugewiesen, und der korrigierte Nettoschub am Ende der 1.000 ft wird auf den Wert der Schubreduzierung gesetzt. (Wenn die ursprüngliche horizontale Entfernung kleiner als 2.000 ft ist, wird eine Hälfte des Segments für die Schubreduzierung verwendet.) Der Endschub am zweiten Teilsegment wird auch auf den Wert der Schubreduzierung gesetzt. Damit wird das zweite Teilsegment mit konstantem Schub geflogen.
B8 Beschleunigter Steigflug und Einfahren der Klappen
Dies schließt sich gewöhnlich an den Anfangssteigflug an. Wie bei allen Flugsegmenten sind die Werte für Anfangshöhe h1, wahre Fluggeschwindigkeit VT1 und Schub (Fn/ δ)1 identisch mit den Endwerten des vorherigen Segments. Die berichtigte Fluggeschwindigkeit VC2 und die mittlere Steigrate ROC am Endpunkt sind Anwendereingaben (Querneigungswinkel ε ist abhängig von Kurvengeschwindigkeit und Kurvenradius). Aufgrund der wechselseitigen Abhängigkeit müssen die Endwerte der Höhe h2, der wahren Fluggeschwindigkeit VT2 und des Schubs (Fn/ δ)2 sowie die Segmentstreckenlänge Δs durch Iteration berechnet werden; die Endhöhe h2 wird eingangs geschätzt und anschließend mit den Gleichungen B-16 und B-17 wiederholt neuberechnet, bis die Differenz zwischen aufeinanderfolgenden Schätzungen kleiner ist als eine entsprechend vorgegebene Toleranz, z.B. 1 ft. Eine praktikable Anfangsschätzung ist h2 = h1 + 250 ft.
Die Schätzung der Segmentstreckenlänge (zurückgelegte horizontale Entfernung) erfolgt durch
|
| (B-17) |
wobei Folgendes gilt:
| 0,95 | Faktor zur Berücksichtigung des Einflusses des Gegenwinds von 8 kt beim Steigen mit 160 kt, |
| k | Konstante zur Konvertierung von Knoten in ft/s = 1,688 ft/s pro kt, |
| VT2 = | wahre Fluggeschwindigkeit am Segmentende, kt VT2 = VC2 / √σ2
wobei: σ2 = Luftdichteverhältnis in Endhöhe h2, |
| αmax = | maximale Beschleunigung im Horizontalflug (ft/s2)
|
| G = | 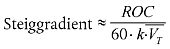
wobei: ROC = Steigrate, ft/min. |
Mit Hilfe dieses Schätzwertes für Δs wird daraufhin die Endhöhe h2' nach folgender Gleichung neu bestimmt:
| h2' = h1 + s · G/0,95 | (B-18) |
So lange der Fehler |h'2 - h2| außerhalb der vorgegebenen Toleranz liegt, so lange werden die Schritte B-17 und B-18 mit den iterativ bestimmten aktuellen Segment-Endwerten für die Höhe h2, die wahre Fluggeschwindigkeit VT2 und den korrigierten Nettoschub je Triebwerk (Fn/ δ)2 wiederholt. Sobald der Fehler im Toleranzbereich liegt, wird der iterative Zyklus beendet und das Beschleunigungssegment bestimmt sich durch die letzten Segment-Endwerte.
Anm.: Falls während des Iterationsprozesses der Fall (amax - G · g) < 0,02 g eintritt, ist die Beschleunigung unter Umständen zu klein, um die gewünschte VC2 in einer angemessenen Entfernung zu erreichen. In diesem Fall kann der Steiggradient auf G = amax/g - 0,02 begrenzt und so die gewünschte Steigrate reduziert werden, um eine akzeptable Beschleunigung aufrechtzuerhalten. Falls G < 0,01, ist daraus zu schlussfolgern, das nicht genügend Schub vorhanden ist, um die angegebene Beschleunigung und Steiggeschwindigkeit zu erreichen; die Berechnung sollte daraufhin beendet und die Verfahrensschritte geändert werden 5.
Die Länge des Beschleunigungssegments wird entsprechend dem Gegenwind w wie folgt korrigiert:
|
| (B-19) |
Beschleunigungssegment mit Schubreduzierung
Die Einrechnung der Schubreduzierung erfolgt hier genauso wie bei einem Segment mit Konstantgeschwindigkeit, wozu die Umwandlung seines ersten Teils in ein Übergangssegment erfolgt. Der Schubreduzierungswert wird so wie im Schubreduzierungsverfahren für Konstantgeschwindigkeit berechnet, und zwar nur nach Gleichung B-1. Es ist anzumerken, dass es in der Regel nicht möglich ist, zu beschleunigen und den Steigflug durchzuführen, während die Schubeinstellung auf Engine-Out-Minimum steht. Dem Schubübergang wird eine Strecke über Grund von 1.000 ft (305 m) zugewiesen und der korrigierte Nettoschub am Ende der 1.000 ft auf den Wert der Schubreduzierung gesetzt. Die Geschwindigkeit für das Ende des Segments wird für eine Segmentlänge von 1.000 ft per Iteration bestimmt. (Wenn die ursprüngliche horizontale Entfernung kleiner als 2.000 ft ist, wird eine Hälfte des Segments für die Schubänderung verwendet.) Der Endschub am zweiten Teilsegment wird auch auf den Wert der Schubreduzierung gesetzt. Damit wird das zweite Teilsegment mit konstantem Schub geflogen.
B9 Zusätzliche Steig- und Beschleunigungssegmente nach Einfahren der Klappen
Enthält die Bahn, in der der Steigflug beginnt, zusätzliche Beschleunigungssegmente, so sollte nochmals mit den Gleichungen B-12 bis B-19 gearbeitet werden, um die Länge des Kurses über Grund, den mittleren Steigwinkel und den jeweiligen Höhenzuwachs zu berechnen. Wie zuvor ist die abschließende Flughöhe über Grund des Segments mittels Iteration zu bestimmen.
B10 Sinkflug und Verzögerung
Beim Anflug muss das Flugzeug normalerweise sinken und die Geschwindigkeit drosseln, um die abschließende Anflugphase vorzubereiten, in der das Flugzeug durch die Betätigung der Landeklappen und das Ausfahren des Fahrwerks konfiguriert wird. Flugmechanisch gibt es keine Änderungen gegenüber dem Abflug; der Hauptunterschied besteht darin, dass das Höhen- und Geschwindigkeitsprofil grundsätzlich bekannt ist und hier für jedes Segment der Triebwerksschub bestimmt werden muss. Die grundlegende Kräftebilanzgleichung lautet
|
| (B-20) |
Gleichung B-20 kann auf zweierlei Art verwendet werden. Zuerst können die Flugzeuggeschwindigkeiten am Anfang und am Ende eines Segments zusammen mit einem Sinkwinkel (oder einer horizontalen Segmentdistanz) sowie mit Anfangs- und Endhöhe des Segments bestimmt werden. In diesem Fall kann die Geschwindigkeitsreduzierung (Abbremsung) nach folgender Gleichung berechnet werden:
|
| (B-21) |
wobei Folgendes gilt: Δs ist der überflogene Flugweg; V1 und V2 sind die Geschwindigkeiten über Grund am Segmentanfang bzw. Segmentende, die nach folgender Gleichung berechnet werden:
|
| (B-22) |
Die Gleichungen B-20, B-21 und B-22 bestätigen, dass, wird die Geschwindigkeit über eine vorgegebene Distanz mit konstanter Sinkrate verringert, ein stärkerer Gegenwind dazu führt, dass zum Erzielen der gleichen Abbremsung mehr Schub benötigt wird, während bei Rückenwind für die gleiche Abbremswirkung weniger Schub erforderlich ist.
In der Praxis erfolgen die meisten, wenn nicht alle Abbremsungen im Anflug mit Leerlaufschub. Für die Zweitanwendung der Gleichung B-20 ist der Schub also als Leerlaufeinstellung definiert, und die Gleichung wird iterativ gelöst, um 1) die Abbremsung und 2) die Flughöhe über Grund am Ende des Abbremssegments zu bestimmen - auf ähnliche Weise wie bei den Beschleunigungssegmenten im Abflug. In diesem Fall kann der Abbremsweg je nach Gegenwind und Rückenwind sehr unterschiedlich sein und mitunter ist für vertretbare Ergebnisse eine Verminderung des Sinkwinkels notwendig.
Der Leerlaufschub ist bei den meisten Flugzeugen kein Nullschub und hängt bei vielen Flugzeugen auch von der Fluggeschwindigkeit ab. Demnach wird zur Lösung der Gleichung B-20 im Anwendungsfall der Abbremsung ein Leerlaufschub eingegeben; der Leerlaufschub wird durch eine Gleichung folgender Art berechnet:
| (Fn/δ)idle = Eidle + Fidle · VC + GA,idle · h + GB,idle · h2 + Hidle · T | (B-23) |
wobei (Eidle, Fidle, GA,idle, GB,idle und Hidle) Leerlaufschub-Triebwerksbeiwerte sind, die in der ANP-Datenbank zur Verfügung stehen.
B11 Landeanflug
Die berichtigte Landeanfluggeschwindigkeit VCA ist über eine Gleichung ähnlich B-11 an das Bruttolandegewicht geknüpft:
| VCA ≈ D ⋅ √W | (B-24) |
wobei der Beiwert D (kt/√lbf) der Landeklappenstellung entspricht.
Die Berechnung des korrigierten Nettoschubs je Triebwerk während des Sinkflugs im Anfluggleitweg erfolgt durch Lösen der Gleichung B-12 nach dem Landegewicht W und der Gleitzahl R entsprechend der Klappenstellung bei ausgefahrenem Fahrwerk. Die Klappenstellung sollte den im tatsächlichen Flugbetrieb typischen Wert annehmen. Beim Landeanflug kann der Gleitwegwinkel γ als konstant angenommen werden. Für düsenbetriebene und mehrmotorige propellergetriebene Flugzeuge ist γ typischerweise - 3°. Für einmotorige propellergetriebene Flugzeuge ist γ typischerweise - 5°.
Zur Berechnung des durchschnittlichen korrigierten Nettoschubs wird Gleichung B-12 unter Anwendung von K = 1,03 umgekehrt, um die Eigenabbremsung eines Flugzeugs zu berücksichtigen, das auf absteigender Flugbahn einem Standardgegenwind von 8 Knoten ausgesetzt ist, während es mit konstanter berichtigter Fluggeschwindigkeit gemäß Gleichung B-24 fliegt, d. h.
|
| (B-25) |
Bei Gegenwind mit anderen Windgeschwindigkeiten als 8 kt berechnet sich der durchschnittliche korrigierte Nettoschub nach
|
| (B-26) |
Die zurückgelegte horizontale Entfernung wird berechnet durch:
|
| (B-27) |
(positiv, weil h1 > h2, und γ ist negativ).
2) Reduzierte Schubwerte nach Anfangssteigflug mit Startleistung.
3) In die Lärmberechnungen werden Untersegmente eingefügt, um Kontursprünge an den Verbindungsstellen zwischen Geradeaus- und Kurvenflug infolge abrupter Änderungen des Querneigungswinkels zu vermeiden und lineare Querneigungswinkelübergänge über die ersten und letzten 5 Grad der Flugkurve zu ermöglichen. In den Leistungsrechnungen ist das nicht notwendig; der Querneigungswinkel ist immer durch Gleichung B-8 gegeben.
4) "Noise Abatement Procedures" ICAO Document 8168 "PANS-OPS" Vol.1 Part V, Chapter 3, ICAO 2004.
5) Das Computermodell sollte in beiden Fällen so programmiert werden, dass der Anwender über die vorliegende Diskrepanz informiert wird.
| Modellierung der seitlichen Streuung des Kurses über Grund | Anlage C |
Bei fehlenden Radardaten wird die Modellierung der seitlichen Streuung des Kurses über Grund empfohlen, ausgehend von der Annahme, dass die Streuung der senkrecht zur Kernstrecke verlaufenden Strecken einer Gaußschen Normalverteilung folgt. Diese Annahme ist erfahrungsgemäß in den meisten Fällen vertretbar.
Bei Annahme einer Gaußschen Verteilung mit einer Standardabweichung S gemäß Abbildung C-1 liegen ca. 98,8 % aller Bewegungen in Grenzbereichen von ± 2,5 x S (d. h. innerhalb eines Flugkorridors mit einer Breite von 5 × S).
Abbildung C-1 Unterteilung eines Kurses über Grund in sieben Unterstrecken.
Die Breite des Flugkorridors beträgt das Fünffache der Standardabweichung der Streuung des Kurses über Grund.
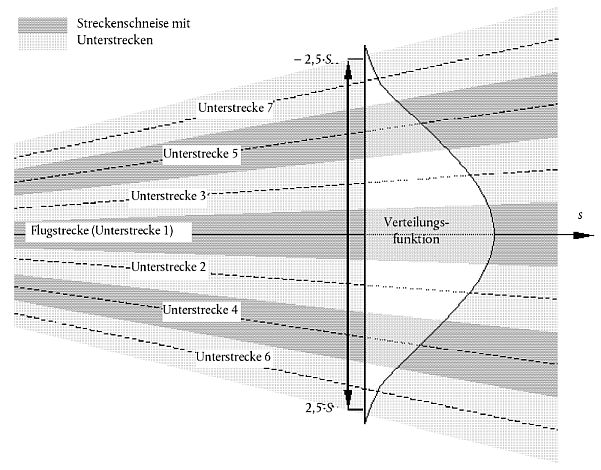 Eine Gaußsche Verteilung lässt sich normalerweise mit sieben einzelnen Unterstrecken hinlänglich modellieren, die sich in gleichmäßigen Abständen in den Grenzbereichen ±2,5 x S des in Abbildung C-1 dargestellten Flugkorridors befinden.
Eine Gaußsche Verteilung lässt sich normalerweise mit sieben einzelnen Unterstrecken hinlänglich modellieren, die sich in gleichmäßigen Abständen in den Grenzbereichen ±2,5 x S des in Abbildung C-1 dargestellten Flugkorridors befinden.
Die Hinlänglichkeit dieser approximativen Bestimmung hängt jedoch vom Verhältnis zwischen der Unterteilung der Strecke in Unterstrecken zu der jeweiligen Flughöhe über Grund ab. Allerdings kann auch der Fall eintreten (Strecken liegen sehr eng beieinander oder sehr verstreut auseinander), dass eine abweichende Anzahl von Unterstrecken besser geeignet ist. Bei zu wenig Unterstrecken kommt es bei der Kontur zu sogenannten "Fingern". In den Tabellen C-1 und C-2 sind die Parameter für eine Untergliederung in 5 bis 13 Unterstrecken aufgeführt. Tabelle C-1 zeigt die Position der einzelnen Unterstrecken, Tabelle C-2 den prozentualen Anteil an den Flugbewegungen je Unterstrecke.
Tabelle C-1 Position von 5, 7, 9, 11 bzw. 13 Unterstrecken
(Die Gesamtbreite des Flugkorridors (auf den 98 % aller Flugbewegungen entfallen) beträgt das Fünffache der Standardabweichung.)
| Unterstrecke Nr. | Position der Unterstrecken bei Untergliederung in | ||||
| 5 Unterstrecken | 7 Unterstrecken | 9 Unterstrecken | 11 Unterstrecken | 13 Unterstrecken | |
| 12/13 | ± 2,31 ·S | ||||
| 10/11 | ± 2,27·S | ± 1,92·S | |||
| 8/9 | ± 2,22·S | ± 1,82·S | ± 1,54·S | ||
| 6/7 | ± 2,14·S | ± 1,67·S | ± 1,36·S | ± 1,15·S | |
| 4/5 | ± 2,00·S | ± 1,43·S | ± 1,11·S | ± 0,91·S | ± 0,77·S |
| 2/3 | ± 1,00·S | ± 0,71·S | ± 0,56·S | ± 0,45·S | ± 0,38·S |
| 1 | 0 | 0 | 0 | 0 | 0 |
Tabelle C-2 Anteil an den Flugbewegungen bei 5, 7, 9, 11 bzw. 13 Unterstrecken
(Die Gesamtbreite der "Schneise" (auf die 98 % aller Flugbewegungen entfallen) beträgt das Fünffache der Standardabweichung.)
| Unterstrecke Nr. | Anteil an den Flugbewegungen auf der Unterstrecke bei Untergliederung in | ||||
| 5 Unterstrecken | 7 Unterstrecken | 9 Unterstrecken | 11 Unterstrecken | 13 Unterstrecken | |
| 12/13 | 1,1 % | ||||
| 10/11 | 1,4 % | 2,5 % | |||
| 8/9 | 2,0 % | 3,5 % | 4,7 % | ||
| 6/7 | 3,1 % | 5,7 % | 7,1 % | 8,0 % | |
| 4/5 | 6,3 % | 10,6 % | 12,1 % | 12,1 % | 11,5 % |
| 2/3 | 24,4 % | 22,2 % | 19,1 % | 16,6 % | 14,4 % |
| 1 | 38,6 % | 28,2 % | 22,2 % | 18,6 % | 15,6 % |
| Neuberechnung von NPD-Daten für Nicht-Referenz-Bedingungen | Anlage D 21 |
Die Schallpegelanteile der einzelnen Segmente der Flugbahn werden von den NPD-Daten abgeleitet, die in der internationalen ANP-Datenbank abgelegt sind. Hierbei ist jedoch zu beachten, dass diese Daten mit Hilfe durchschnittlicher atmosphärischer Dämpfungsraten gemäß SAE-AIR-1845 normalisiert wurden. Diese Raten sind Durchschnitte von Werten, die im Rahmen der Prüfungen zur Lärmzertifizierung von Luftfahrzeugen in Europa und in den USA ermittelt wurden. Die große Schwankungsbreite der atmosphärischen Bedingungen (Temperatur und relative Luftfeuchtigkeit) während dieser Tests ist in Abbildung D-1 dargestellt.
Abbildung D-1 Während der Lärmzertifizierungsprüfungen aufgezeichnete meteorologische Bedingungen
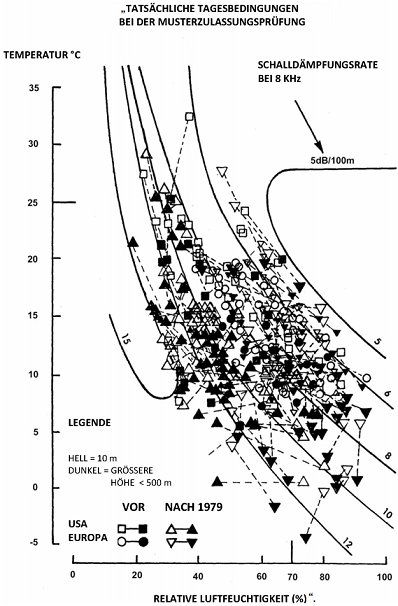
Die Kurven in Abbildung D-1, die mit Hilfe eines Industrienormmodells der atmosphärischen Dämpfung ARP 866A berechnet wurden, zeigen, dass über die Prüfbedingungen hinweg mit einer erheblichen Schwankung der hochfrequenten (8 kHz) Schallabsorption zu rechnen wäre (obwohl die Schwankung der Gesamtabsorption vergleichsweise gering wäre).
Da die in Tabelle D-1 angegebenen Dämpfungsraten arithmetische Mittelwerte sind, kann der komplette Satz nicht auf eine einzelne Referenzatmosphäre (d. h. auf keine spezifischen Werte für Temperatur und relative Luftfeuchtigkeit) bezogen werden. Die Dämpfungsraten lassen sich nur als Eigenschaften einer rein fiktiven Atmosphäre begreifen, die als "AIR-1845-Atmosphäre" bezeichnet wird.
Tabelle D-1 Verwendete durchschnittliche atmosphärische Dämpfungsraten für die Normalisierung von NPD-Daten in der ANP-Datenbank
| Mittenfrequenz des Terzbandes [Hz] | Dämpfungsrate [dB/100m] | Mittenfrequenz des Terzbandes [Hz] | Dämpfungsrate [dB/100m] |
| 50 | 0,033 | 800 | 0,459 |
| 63 | 0,033 | 1.000 | 0,590 |
| 80 | 0,033 | 1.250 | 0,754 |
| 100 | 0,066 | 1.600 | 0,983 |
| 125 | 0,066 | 2.000 | 1,311 |
| 160 | 0,098 | 2.500 | 1,705 |
| 200 | 0,131 | 3.150 | 2,295 |
| 250 | 0,131 | 4.000 | 3,115 |
| 315 | 0,197 | 5.000 | 3,607 |
| 400 | 0,230 | 6.300 | 5,246 |
| 500 | 0,295 | 8.000 | 7,213 |
| 630 | 0,361 | 10.000 | 9,836 |
Bei den Dämpfungskoeffizienten in Tabelle D-1 kann davon ausgegangen werden, dass sie hinsichtlich Temperatur und relativer Luftfeuchtigkeit über angemessene Bereiche hinweg gültig sind. Um jedoch etwaigen Anpassungsbedarf zu prüfen, sollten mithilfe von SAE ARP-5534 mittlere Luftabsorptionskoeffizienten für die durchschnittliche Flugplatztemperatur T und die relative Luftfeuchtigkeit RH berechnet werden. Sollten die auf diese Weise gewonnenen Werte nach Vergleich mit den Werten aus Tabelle D-1 einen Anpassungsbedarf erkennen lassen, so sollte nach der im Folgenden geschilderten Methodik vorgegangen werden.
Die ANP-Datenbank stellt für jede Leistungseinstellung die folgenden NPD-Daten bereit:
wobei alle Daten entsprechend der AIR-1845-Atmosphäre normalisiert sind.
Die Anpassung der NPD-Kurven an anwenderspezifische Bedingungen T und RH erfolgt in drei Schritten:
| Ln(dref) = Ln,ref(dref) + αn,ref · dref | (D-1) |
wobei: Ln(dref) - ungedämpftes Spektrum bei dref = 305m und αn,ref - Beiwert der Luftabsorption für Frequenzband n aus Tabelle D-1 (aber ausgedrückt in dB/m).
| Ln,ref(di) = Ln(dref)-20.lg(di/dref) -αn,ref · di | (D-2) |
| Ln,5534 (T,RH,di) = Ln(dref) - 20.lg(di/dref) -αn,5534 (T,RH) di | (D-3) |
Hierbei ist αn,5534 der Koeffizient der Luftabsorption für das Frequenzband n (ausgedrückt in dB/m), berechnet mithilfe von SAE ARP-5534 mit der Temperatur T und der relativen Luftfeuchtigkeit RH.
|
| (D-4) |
Das Inkrement ΔL ist die Differenz zwischen den NPD-Werten in der anwenderspezifischen Atmosphäre und in der Referenzatmosphäre. Dies wird zum NPD-Datenwert der ANP-Datenbank hinzuaddiert, um die entsprechend angepassten NPD-Daten abzuleiten.
Bei der Anwendung von ΔL zur Anpassung der NPD-Werte sowohl von Lmax als auch von LE wird praktisch unterstellt, dass unterschiedliche atmosphärische Bedingungen ausschließlich das Referenzspektrum beeinflussen und keine Wirkung auf die Form des Pegel-Zeit-Verlaufs haben. Es kann davon ausgegangen werden, dass dies für typische Ausbreitungsbereiche und typische atmosphärische Bedingungen gültig ist.
| Korrektur aufgrund des endlichen Segments | Anlage E |
Diese Anlage enthält die Ableitung der Korrektur aufgrund des endlichen Segments und des damit verbundenen Energieanteilsalgorithmus gemäß Abschnitt 2.7.19.
E1 Geometrie
Der Energieanteilsalgorithmus basiert auf der Schallabstrahlung einer 90-Grad-Dipolschallquelle der vierten Potenz. Die Richtungseigenschaften ähneln den Schallverhältnissen von Düsenflugzeugen zumindest in dem Winkelbereich, der die Schallereignispegel unter und seitlich der Flugbahn des Luftfahrzeugs am meisten beeinflusst.
Abbildung E-1 Geometrie zwischen Flugbahn und Beobachterstandort O
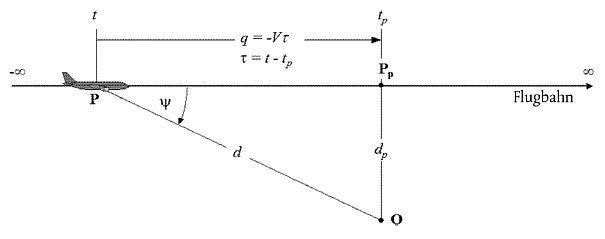
Abbildung E-1 illustriert die Geometrie der Schallausbreitung zwischen der Flugbahn und dem Standort des Beobachters O. Das Luftfahrzeug in P fliegt in stiller gleichförmiger Luft mit einer konstanten Geschwindigkeit auf einer geraden, horizontalen Flugbahn. Der Punkt des kleinsten Vorbeiflugabstands vom Beobachter ist Pp. Die Parameter sind
d Abstand des Beobachters zum Luftfahrzeug,
dp senkrechter Abstand zwischen dem Beobachter und der Flugbahn (Schrägabstand),
q Abstand P zu Pp = - V x τ
V Geschwindigkeit des Luftfahrzeugs,
t Zeit, zu der sich das Luftfahrzeug an Punkt P befindet,
tp Zeit, zu der sich das Luftfahrzeug am Punkt des kleinsten Vorbeiflugabstands Pp befindet,
τ Flugzeit = Zeit in Bezug auf Zeitpunkt Pp = t - tp,
ψ Winkel zwischen Flugbahn und Luftfahrzeug-Beobachter-Vektor
Es ist zu beachten, dass die Flugzeit τ in Bezug auf den Punkt des kleinsten Vorbeiflugabstands negativ ist, wenn sich das Luftfahrzeug vor der Position des Beobachters befindet (wie in Abbildung E-1 dargestellt) und dass in diesem Fall somit die relative Entfernung q bis zum Punkt des kleinsten Vorbeiflugabstands positiv wird. Hat das Luftfahrzeug den Beobachter passiert, wird q negativ.
E2 Schätzung des Energieanteils
Das Grundkonzept des Energieanteils besteht darin, die an der Beobachterposition erzeugte Lärmexposition E aus einem Flugbahnsegment P1P2 (mit einem Anfangspunkt P1 und einem Endpunkt P2) auszudrücken, indem die Exposition E∞ aus der gesamten unendlichen Vorbeiflugbahn mit einem einfachen Faktor multipliziert wird - dem Energieanteils-Faktor F:
| E = F · E∞ | (E-1) |
Da die Exposition in Bezug auf das Zeitintegral des mittleren quadratischen (gewichteten) Schalldruckpegels ausgedrückt werden kann, d. h.
|
| (E-2) |
muss zur Berechnung von E der mittlere quadratische Schalldruck in Abhängigkeit von den bekannten geometrischen und betrieblichen Parametern ausgedrückt werden. Das bedeutet für eine 90°-Dipolschallquelle:
|
| (E-3) |
wobei p2 und pp2 - die beobachteten mittleren quadratischen Schalldrücke, die vom Luftfahrzeug beim Passieren der Punkte P und Pp erzeugt werden.
Es hat sich gezeigt, dass dieses relativ einfache Verhältnis den Düsenflugzeuglärm gut nachbildet, obwohl die wirklichen Mechanismen äußerst kompliziert sind. Der Term dp2 /d2 in Gleichung E-3 beschreibt nur den Mechanismus der bei einer Punktquelle üblichen kugelförmigen Abstrahlung, unendlichen Schallgeschwindigkeit und gleichförmigen, nichtdissipativen Atmosphäre. Alle anderen physikalischen Effekte - Richtcharakteristik der Schallquelle, endliche Schallgeschwindigkeit, Luftabsorption, Doppler-Effekt usw. - werden implizit im Term sin2ψ erfasst. Dieser Faktor bewirkt die inverse Abnahme des mittleren quadratischen Schalldrucks als d2; daher der Ausdruck Schallquelle "vierter Potenz".
Mit den Substitutionen
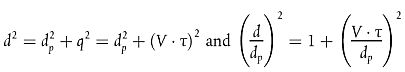
kann der mittlere quadratische Schalldruck in Abhängigkeit von der Zeit ausgedrückt werden (wobei die Schallausbreitungszeit wiederum unberücksichtigt bleibt):
|
| (E-4) |
Wird dies in die Gleichung (E-2) eingesetzt und die Substitution durchgeführt
| α = (V ⋅ τ ) / dp | (E-5) |
kann die Schallexposition am Beobachtungsort aus dem Vorbeiflug im Zeitintervall [τ1, τ2] ausgedrückt werden als
|
| (E-6) |
Die Lösung dieses Integrals ist
|
| (E-7) |
Die Integration über das Intervall [- ∞,+ ∞] (d. h. über die gesamte unendliche Flugbahn) ergibt den folgenden Ausdruck für die Gesamtexposition E:
|
| (E-8) |
und damit ergibt sich für den Energieanteil nach Gleichung E-1
|
| (E-9) |
E3 Widerspruchsfreiheit zwischen den Höchst- und den zeitintegrierten Werten - Der skalierte Abstand
Eine Konsequenz aus der Verwendung des einfachen Dipolmodells bei der Bestimmung des Energieanteils ist die implizite Unterstellung einer spezifischen theoretischen Differenz ΔL zwischen den Schallereignispegeln Lmax und LE. Wenn das Konturenmodell in sich widerspruchsfrei sein soll, muss diese Differenz gleich der Differenz der aus den NPD- Kurven bestimmten Werte sein. Ein Problem besteht darin, dass die NPD-Daten von Messungen des tatsächlichen Fluglärms abgeleitet sind und nicht zwangsläufig mit der einfachen Theorie übereinstimmen. Deshalb muss die Theorie um ein flexibles Element erweitert werden. Da die Variablen α1 und α2 aber grundsätzlich über Geometrie und Flugzeuggeschwindigkeit bestimmt werden, gibt es hier keinen zusätzlichen Freiraum. Eine Lösung bietet das Konzept eines skalierten Abstands dλ, das wie folgt aussieht.
Der Expositionspegel LE,∞ der in der ANP-Datenbank in tabellarischer Form in Abhängigkeit von dp für eine Referenzgeschwindigkeit Vref, enthalten ist, kann ausgedrückt werden als
|
| (E-10) |
wobei: p0 - ein Standard-Referenzdruck und tref - eine Referenzzeit (= 1 s für SEL). Das ergibt für die tatsächliche Geschwindigkeit V
|
| (E-11) |
Dementsprechend lässt sich der maximale Schallereignispegel Lmax wie folgt ausdrücken:
|
| (E-12) |
Für die Dipolschallquelle kann mit Hilfe der Gleichungen E-8, E-11 und E-12 unter Berücksichtigung von (aus Gleichungen E-2 und E-8) 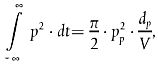 die Differenz ΔL wie folgt dargestellt werden:
die Differenz ΔL wie folgt dargestellt werden:
|
| (E-13) |
Diese kann nur dann dem aus den NPD-Daten ermittelten Wert von ΔL entsprechen, wenn der zur Berechnung des Energieanteils verwendete Schrägabstand dp durch einen skalierten Abstand dλ ersetzt wird, der gegeben ist durch
|
| (E-14a) |
oder
|
| (E-14b) |
Bei Ersatz von dp durch dλ in Gleichung E-5 und Verwendung der Definition q = Vτ aus Abbildung E-1 lassen sich die Parameter α1 und α2 in Gleichung E-9 wie folgt schreiben (indem q = q1 an den Anfangspunkt und q - λ = q2 an den Endpunkt eines Flugbahnlängensegments λ gesetzt wird)
|
|
Da der eigentliche Schrägabstand durch einen skalierten Abstand ersetzt werden muss, verringert sich die Einfachheit des 90-Grad-Dipolmodells der vierten Potenz. Andererseits erfährt das Modell durch die Verwendung von messwertbezogenen Daten eine In-situ-Kalibrierung, so dass der Algorithmus zur Berechnung des Energieanteils als halbempirisch angesehen werden kann und nicht mehr nur rein theoretisch ist.
| Datenbank für die Lärmquelle Strassenverkehr | Anlage F 21 |
In dieser Anlage wird die Datenbank für den größten Teil der bestehenden Quellen für Straßenverkehrslärm dargestellt, die zur Berechnung von Straßenverkehrslärm anhand der in 2.2 Straßenverkehrslärm beschriebenen Methode heranzuziehen ist.
Tabelle F-1: Koeffizienten AR,i,m und BR,i,m für Rollgeräusche sowie AP,i,m und BP,i,m für Antriebsgeräusche 21
| Kategorie | Koeffizient | 63 | 125 | 250 | 500 | 1.000 | 2.000 | 4.000 | 8.000 |
| 1 | AR | 83,1 | 89,2 | 87,7 | 93,1 | 100,1 | 96,7 | 86,8 | 76,2 |
| BR | 30,0 | 41,5 | 38,9 | 25,7 | 32,5 | 37,2 | 39,0 | 40,0 | |
| AP | 97,9 | 92,5 | 90,7 | 87,2 | 84,7 | 88,0 | 84,4 | 77,1 | |
| BP | -1,3 | 7,2 | 7,7 | 8,0 | 8,0 | 8,0 | 8,0 | 8,0 | |
| 2 | AR | 88,7 | 93,2 | 95,7 | 100,9 | 101,7 | 95,1 | 87,8 | 83,6 |
| BR | 30,0 | 35,8 | 32,6 | 23,8 | 30,1 | 36,2 | 38,3 | 40,1 | |
| AP | 105,5 | 100,2 | 100,5 | 98,7 | 101,0 | 97,8 | 91,2 | 85,0 | |
| BP | -1,9 | 4,7 | 6,4 | 6,5 | 6,5 | 6,5 | 6,5 | 6,5 | |
| 3 | AR | 91,7 | 96,2 | 98,2 | 104,9 | 105,1 | 98,5 | 91,1 | 85,6 |
| BR | 30,0 | 33,5 | 31,3 | 25,4 | 31,8 | 37,1 | 38,6 | 40,6 | |
| AP | 108,8 | 104,2 | 103,5 | 102,9 | 102,6 | 98,5 | 93,8 | 87,5 | |
| BP | 0,0 | 3,0 | 4,6 | 5,0 | 5,0 | 5,0 | 5,0 | 5,0 | |
| 4a | AR | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| BR | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |
| AP | 93,0 | 93,0 | 93,5 | 95,3 | 97,2 | 100,4 | 95,8 | 90,9 | |
| BP | 4,2 | 7,4 | 9,8 | 11,6 | 15,7 | 18,9 | 20,3 | 20,6 | |
| 4b | AR | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| BR | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |
| AP | 99,9 | 101,9 | 96,7 | 94,4 | 95,2 | 94,7 | 92,1 | 88,6 | |
| BP | 3,2 | 5,9 | 11,9 | 11,6 | 11,5 | 12,6 | 11,1 | 12,0 | |
| 5 | AR | ||||||||
| BR | |||||||||
| AP | |||||||||
| BP |
Tabelle F-2: Koeffizienten ai und bi für Spikereifen
| Kategorie | Koeffizient | 63 | 125 | 250 | 500 | 1.000 | 2.000 | 4.000 | 8.000 |
| 1 | ai bi | 0,0 0,0 | 0,0 0,0 | 0,0 0,0 | 2,6 - 3,1 | 2,9 - 6,4 | 1,5 - 14,0 | 2,3 - 22,4 | 9,2 - 11,4 |
Tabelle F-3: Koeffizienten CR,m,k und CP,m,k für Beschleunigung und Abbremsen
| Kategorie | k | Cr | Cp |
| 1 | 1= Kreuzung 2=Kreisverkehr | - 4,5 - 4,4 | 5,5 3,1 |
| 2 | 1= Kreuzung 2=Kreisverkehr | -4 - 2,3 | 9 6,7 |
| 3 | 1= Kreuzung 2=Kreisverkehr | -4 - 2,3 | 9 6,7 |
| 4a | 1= Kreuzung 2=Kreisverkehr | 0 0 | 0 0 |
| 4b | 1= Kreuzung 2=Kreisverkehr | 0 0 | 0 0 |
| 5 | 1= Kreuzung 2=Kreisverkehr |
Tabelle F-4: Koeffizienten αi,m und βm für die Straßenoberfläche 21
| Beschreibung | Mindestgeschwindigkeit, bei der der Wert gilt [km/h] | Höchstgeschwindigkeit, bei der der Wert gilt [km/h] | Kategorie | αm (63 Hz) | αm (125 Hz) | αm (250 Hz) | αm (500 Hz) | αm (1 kHz) | αm (2 kHz) | αm (4 kHz) | αm (8 kHz) | ßm |
| Referenzoberfläche | - | - | 1 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 2 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| 3 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| 1-layer ZOAB | 50 | 130 | 1 | 0,0 | 5,4 | 4,3 | 4,2 | -1,0 | -3,2 | -2,6 | 0,8 | -6,5 |
| 2 | 7,9 | 4,3 | 5,3 | -0,4 | -5,2 | -4,6 | -3,0 | -1,4 | 0,2 | |||
| 3 | 9,3 | 5,0 | 5,5 | -0,4 | -5,2 | -4,6 | -3,0 | -1,4 | 0,2 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| 2-layer ZOAB | 50 | 130 | 1 | 1,6 | 4,0 | 0,3 | -3,0 | -4,0 | -6,2 | -4,8 | -2,0 | -3,0 |
| 2 | 7,3 | 2,0 | -0,3 | -5,2 | -6,1 | -6,0 | -4,4 | -3,5 | 4,7 | |||
| 3 | 8,3 | 2,2 | -0,4 | -5,2 | -6,2 | -6,1 | -4,5 | -3,5 | 4,7 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| 2-layer ZOAB (fine) | 80 | 130 | 1 | -1,0 | 3,0 | -1,5 | -5,3 | -6,3 | -8,5 | -5,3 | -2,4 | -0,1 |
| 2 | 7,9 | 0,1 | -1,9 | -5,9 | -6,1 | -6,8 | -4,9 | -3,8 | -0,8 | |||
| 3 | 9,4 | 0,2 | -1,9 | -5,9 | -6,1 | -6,7 | -4,8 | -3,8 | -0,9 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| SMA-NL5 | 40 | 80 | 1 | 10,3 | -0,9 | 0,9 | 1,8 | -1,8 | -2,7 | -2,0 | -1,3 | -1,6 |
| 2 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| 3 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| SMA-NL8 | 40 | 80 | 1 | 6,0 | 0,3 | 0,3 | 0,0 | -0,6 | -1,2 | -0,7 | -0,7 | -1,4 |
| 2 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| 3 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| Brushed down concrete | 70 | 120 | 1 | 8,2 | -0,4 | 2,8 | 2,7 | 2,5 | 0,8 | -0,3 | -0,1 | 1,4 |
| 2 | 0,3 | 4,5 | 2,5 | -0,2 | -0,1 | -0,5 | -0,9 | -0,8 | 5,0 | |||
| 3 | 0,2 | 5,3 | 2,5 | -0,2 | -0,1 | -0,6 | -1,0 | -0,9 | 5,5 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| Optimised brushed down concrete | 70 | 80 | 1 | -0,2 | -0,7 | 1,4 | 1,2 | 1,1 | -1,6 | -2,0 | -1,8 | 1,0 |
| 2 | -0,7 | 3,0 | -2,0 | -1,4 | -1,8 | -2,7 | -2,0 | -1,9 | -6,6 | |||
| 3 | -0,5 | 4,2 | -1,9 | -1,3 | -1,7 | -2,5 | -1,8 | -1,8 | -6,6 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| Fine broomed concrete | 70 | 120 | 1 | 8,0 | -0,7 | 4,8 | 2,2 | 1,2 | 2,6 | 1,5 | -0,6 | 7,6 |
| 2 | 0,2 | 8,6 | 7,1 | 3,2 | 3,6 | 3,1 | 0,7 | 0,1 | 3,2 | |||
| 3 | 0,1 | 9,8 | 7,4 | 3,2 | 3,1 | 2,4 | 0,4 | 0,0 | 2,0 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| Worked surface | 50 | 130 | 1 | 8,3 | 2,3 | 5,1 | 4,8 | 4,1 | 0,1 | -1,0 | -0,8 | -0,3 |
| 2 | 0,1 | 6,3 | 5,8 | 1,8 | -0,6 | -2,0 | -1,8 | -1,6 | 1,7 | |||
| 3 | 0,0 | 7,4 | 6,2 | 1,8 | -0,7 | -2,1 | -1,9 | -1,7 | 1,4 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| Hard elements in herringbone | 30 | 60 | 1 | 27,0 | 16,2 | 14,7 | 6,1 | 3,0 | -1,0 | 1,2 | 4,5 | 2,5 |
| 2 | 29,5 | 20,0 | 17,6 | 8,0 | 6,2 | -1,0 | 3,1 | 5,2 | 2,5 | |||
| 3 | 29,4 | 21,2 | 18,2 | 8,4 | 5,6 | -1,0 | 3,0 | 5,8 | 2,5 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| Hard elements not in herringbone | 30 | 60 | 1 | 31,4 | 19,7 | 16,8 | 8,4 | 7,2 | 3,3 | 7,8 | 9,1 | 2,9 |
| 2 | 34,0 | 23,6 | 19,8 | 10,5 | 11,7 | 8,2 | 12,2 | 10,0 | 2,9 | |||
| 3 | 33,8 | 24,7 | 20,4 | 10,9 | 10,9 | 6,8 | 12,0 | 10,8 | 2,9 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| Quiet hard elements | 30 | 60 | 1 | 26,8 | 13,7 | 11,9 | 3,9 | -1,8 | -5,8 | -2,7 | 0,2 | -1,7 |
| 2 | 9,2 | 5,7 | 4,8 | 2,3 | 4,4 | 5,1 | 5,4 | 0,9 | 0,0 | |||
| 3 | 9,1 | 6,6 | 5,2 | 2,6 | 3,9 | 3,9 | 5,2 | 1,1 | 0,0 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| Thin layer A | 40 | 130 | 1 | 10,4 | 0,7 | -0,6 | -1,2 | -3,0 | -4,8 | -3,4 | -1,4 | -2,9 |
| 2 | 13,8 | 5,4 | 3,9 | -0,4 | -1,8 | -2,1 | -0,7 | -0,2 | 0,5 | |||
| 3 | 14,1 | 6,1 | 4,1 | -0,4 | -1,8 | -2,1 | -0,7 | -0,2 | 0,3 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |||
| Thin layer B | 40 | 130 | 1 | 6,8 | -1,2 | -1,2 | -0,3 | -4,9 | -7,0 | -4,8 | -3,2 | -1,8 |
| 2 | 13,8 | 5,4 | 3,9 | -0,4 | -1,8 | -2,1 | -0,7 | -0,2 | 0,5 | |||
| 3 | 14,1 | 6,1 | 4,1 | -0,4 | -1,8 | -2,1 | -0,7 | -0,2 | 0,3 | |||
| 4a/4b | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| Datenbank für Eisenbahnquelle | Anlage G 21 |
In dieser Anlage wird die Datenbank für den größten Teil der bestehenden Eisenbahnlärmquellen dargestellt, die zur Berechnung von Eisenbahnlärm anhand der in 2.3 Eisenbahnlärm beschriebenen Methode heranzuziehen ist.
Tabelle G-1: Koeffizienten Lr,TR,i und Lr,VEH,i für Schienen- und Radrauheit 21
|
Lr,VEH,i | |||
| Wellenlänge |
Bremsentyp | ||
| c | k | n | |
| Klotzbremse mit Bremsklotzsohlen aus Grauguss | Verbundstoffbremse | Scheibenbremse | |
| 1.000 mm | 2,2 | - 4,0 | - 5,9 |
| 800 mm | 2,2 | - 4,0 | - 5,9 |
| 630 mm | 2,2 | - 4,0 | - 5,9 |
| 500 mm | 2,2 | - 4,0 | - 5,9 |
| 400 mm | 2,2 | - 4,0 | - 5,9 |
| 315 mm | 2,2 | - 4,0 | - 5,9 |
| 250 mm | 2,2 | - 4,0 | 2,3 |
| 200 mm | 2,2 | - 4,0 | 2,8 |
| 160 mm | 2,4 | - 4,0 | 2,6 |
| 120 mm | 0,6 | - 4,0 | 1,2 |
| 100 mm | 2,6 | - 4,0 | 2,1 |
| 80 mm | 5,8 | - 4,3 | 0,9 |
| 63 mm | 8,8 | - 4,6 | - 0,3 |
| 50 mm | 11,1 | - 4,9 | - 1,6 |
| 40 mm | 11,0 | - 5,2 | - 2,9 |
| 31,5 mm | 9,8 | - 6,3 | - 4,9 |
| 25 mm | 7,5 | - 6,8 | - 7,0 |
| 20 mm | 5,1 | - 7,2 | - 8,6 |
| 16 mm | 3,0 | - 7,3 | - 9,3 |
| 12 mm | 1,3 | - 7,3 | - 9,5 |
| 10 mm | 0,2 | - 7,1 | - 10,1 |
| 8 mm | - 0,7 | - 6,9 | - 10,3 |
| 6,3 mm | - 1,2 | - 6,7 | - 10,3 |
| 5 mm | - 1,0 | - 6,0 | - 10,8 |
| 4 mm | 0,3 | - 3,7 | - 10,9 |
| 3,2 mm | 0,2 | - 2,4 | - 9,5 |
| 2,5 mm | 1,3 | - 2,6 | - 9,5 |
| 2 mm | 3,1 | - 2,5 | - 9,5 |
| 1,6 mm | 3,1 | - 2,5 | - 9,5 |
| 1,2 mm | 3,1 | - 2,5 | - 9,5 |
| 1 mm | 3,1 | - 2,5 | - 9,5 |
| 0,8 mm | 3,1 | - 2,5 | - 9,5 |
(Stand: 28.07.2021)
| Lr,TR,i | ||
| Wellenlänge | Schienenrauheit | |
| E | M | |
| EN ISO 3095:2013 (Guter Wartungszustand, sehr glatt) | Durchschnittliches Netz (Normaler Wartungszustand, glatt) | |
| 2.000 mm | 17,1 | 35,0 |
| 1.600 mm | 17,1 | 31,0 |
| 1.250 mm | 17,1 | 28,0 |
| 1.000 mm | 17,1 | 25,0 |
| 800 mm | 17,1 | 23,0 |
| 630 mm | 17,1 | 20,0 |
| 500 mm | 17,1 | 17,0 |
| 400 mm | 17,1 | 13,5 |
| 315 mm | 15,0 | 10,5 |
| 250 mm | 13,0 | 9,0 |
| 200 mm | 11,0 | 6,5 |
| 160 mm | 9,0 | 5,5 |
| 125 mm | 7,0 | 5,0 |
| 100 mm | 4,9 | 3,5 |
| 80 mm | 2,9 | 2,0 |
| 63 mm | 0,9 | 0,1 |
| 50 mm | -1,1 | -0,2 |
| 40 mm | -3,2 | -0,3 |
| 31,5 mm | -5,0 | -0,8 |
| 25 mm | -5,6 | -3,0 |
| 20 mm | -6,2 | -5,0 |
| 16 mm | -6,8 | -7,0 |
| 12,5 mm | -7,4 | -8,0 |
| 10 mm | -8,0 | -9,0 |
| 8 mm | -8,6 | -10,0 |
| 6,3 mm | -9,2 | -12,0 |
| 5 mm | -9,8 | -13,0 |
| 4 mm | -10,4 | -14,0 |
| 3,15 mm | -11,0 | -15,0 |
| 2,5 mm | -11,6 | -16,0 |
| 2 mm | -12,2 | -17,0 |
| 1,6 mm | -12,8 | -18,0 |
| 1,25 mm | -13,4 | -19,0 |
| 1 mm | -14,0 | -19,0 |
| 0,8 mm | -14,0 | -19,0 |
Tabelle G-2: Koeffizienten A3,i für den Kontaktfilter 21
| A3,i | |||||
| 1.1. Wellenlänge | Achslast 50 kN - Raddurchmesser 360 mm | Achslast 50 kN - Raddurchmesser 680 mm | Achslast 50 kN - Raddurchmesser 920 mm | Achslast 25 kN - Raddurchmesser 920 mm | Achslast 100 kN - Raddurchmesser 920 mm |
| 2.000 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 1.600 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 1.250 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 1.000 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 800 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 630 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 500 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 400 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 315 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 250 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 200 mm | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 160 mm | 0,0 | 0,0 | 0,0 | 0,0 | -0,1 |
| 125 mm | 0,0 | 0,0 | -0,1 | 0,0 | -0,2 |
| 100 mm | 0,0 | -0,1 | -0,1 | 0,0 | -0,3 |
| 80 mm | -0,1 | -0,2 | -0,3 | -0,1 | -0,6 |
| 63 mm | -0,2 | -0,3 | -0,6 | -0,3 | -1,0 |
| 50 mm | -0,3 | -0,7 | -1,1 | -0,5 | -1,8 |
| 40 mm | -0,6 | -1,2 | -1,3 | -1,1 | -3,2 |
| 31,5 mm | -1,0 | -2,0 | -3,5 | -1,8 | -5,4 |
| 25 mm | -1,8 | -4,1 | -5,3 | -3,3 | -8,7 |
| 20 mm | -3,2 | -6,0 | -8,0 | -5,3 | -12,2 |
| 16 mm | -5,4 | -9,2 | -12,0 | -7,9 | -16,7 |
| 12,5 mm | -8,7 | -13,8 | -16,8 | -12,8 | -17,7 |
| 10 mm | -12,2 | -17,2 | -17,7 | -16,8 | -17,8 |
| 8 mm | -16,7 | -17,7 | -18,0 | -17,7 | -20,7 |
| 6,3 mm | -17,7 | -18,6 | -21,5 | -18,2 | -22,1 |
| 5 mm | -17,8 | -21,5 | -21,8 | -20,5 | -22,8 |
| 4 mm | -20,7 | -22,3 | -22,8 | -22,0 | -24,0 |
| 3,15 mm | -22,1 | -23,1 | -24,0 | -22,8 | -24,5 |
| 2,5 mm | -22,8 | -24,4 | -24,5 | -24,2 | -24,7 |
| 2 mm | -24,0 | -24,5 | -25,0 | -24,5 | -27,0 |
| 1,6 mm | -24,5 | -25,0 | -27,3 | -25,0 | -27,8 |
| 1,25 mm | -24,7 | -28,0 | -28,1 | -27,4 | -28,6 |
| 1 mm | -27,0 | -28,8 | -28,9 | -28,2 | -29,4 |
| 0,8 mm | -27,8 | -29,6 | -29,7 | -29,0 | -30,2 " |
Tabelle G-3: Koeffizienten LH,TR,i LH,VEH,i und LH,VEH,SUP,i für Transferfunktionen 21
(Werte sind ausgedrückt in Schallleistungspegel pro Achse)
| LH,TR,i | ||||||||
| Frequenz | Unterbau/Art der Zwischenlage | |||||||
| M/S | M/M | M/H | B/S | B/M | B/H | W | D | |
| Monoblock-Schwelle auf weicher Zwischenlage | Monoblock-Schwelle auf mittlerer Zwischenlage | Monoblock-Schwelle auf harter Zwischenlage | Zweiblock-Schwelle auf weicher Zwischenlage | Zweiblock-Schwelle auf mittlerer Zwischenlage | Zweiblock-Schwelle auf harter Zwischenlage | Holzschwellen | Direkte Befestigung auf Brücken | |
| 50 Hz | 53,3 | 50,9 | 50,1 | 50,9 | 50,0 | 49,8 | 44,0 | 75,4 |
| 63 Hz | 59,3 | 57,8 | 57,2 | 56,6 | 56,1 | 55,9 | 51,0 | 77,4 |
| 80 Hz | 67,2 | 66,5 | 66,3 | 64,3 | 64,1 | 64,0 | 59,9 | 81,4 |
| 100 Hz | 75,9 | 76,8 | 77,2 | 72,3 | 72,5 | 72,5 | 70,8 | 87,1 |
| 125 Hz | 79,2 | 80,9 | 81,6 | 75,4 | 75,8 | 75,9 | 75,1 | 88,0 |
| 160 Hz | 81,8 | 83,3 | 84,0 | 78,5 | 79,1 | 79,4 | 76,9 | 89,7 |
| 200 Hz | 84,2 | 85,8 | 86,5 | 81,8 | 83,6 | 84,4 | 77,2 | 83,4 |
| 250 Hz | 88,6 | 90,0 | 90,7 | 86,6 | 88,7 | 89,7 | 80,9 | 87,7 |
| 316 Hz | 91,0 | 91,6 | 92,1 | 89,1 | 89,6 | 90,2 | 85,3 | 89,8 |
| 400 Hz | 94,5 | 93,9 | 94,3 | 91,9 | 89,7 | 90,2 | 92,5 | 97,5 |
| 500 Hz | 97,0 | 95,6 | 95,8 | 94,5 | 90,6 | 90,8 | 97,0 | 99,0 |
| 630 Hz | 99,2 | 97,4 | 97,0 | 97,5 | 93,8 | 93,1 | 98,7 | 100,8 |
| 800 Hz | 104,0 | 101,7 | 100,3 | 104,0 | 100,6 | 97,9 | 102,8 | 104,9 |
| 1.000 Hz | 107,1 | 104,4 | 102,5 | 107,9 | 104,7 | 101,1 | 105,4 | 111,8 |
| 1.250 Hz | 108,3 | 106,0 | 104,2 | 108,9 | 106,3 | 103,4 | 106,5 | 113,9 |
| 1.600 Hz | 108,5 | 106,8 | 105,4 | 108,8 | 107,1 | 105,4 | 106,4 | 115,5 |
| 2.000 Hz | 109,7 | 108,3 | 107,1 | 109,8 | 108,8 | 107,7 | 107,5 | 114,9 |
| 2.500 Hz | 110,0 | 108,9 | 107,9 | 110,2 | 109,3 | 108,5 | 108,1 | 118,2 |
| 3.160 Hz | 110,0 | 109,1 | 108,2 | 110,1 | 109,4 | 108,7 | 108,4 | 118,3 |
| 4.000 Hz | 110,0 | 109,4 | 108,7 | 110,1 | 109,7 | 109,1 | 108,7 | 118,4 |
| 5.000 Hz | 110,3 | 109,9 | 109,4 | 110,3 | 110,0 | 109,6 | 109,1 | 118,9 |
| 6.350 Hz | 110,0 | 109,9 | 109,7 | 109,9 | 109,8 | 109,6 | 109,1 | 117,5 |
| 8.000 Hz | 110,1 | 110,3 | 110,4 | 110,0 | 110,0 | 109,9 | 109,5 | 117,9 |
| 10.000 Hz | 110,6 | 111,0 | 111,4 | 110,4 | 110,5 | 110,6 | 110,2 | 118,6 |
(Stand: 28.07.2021)
|
LH,VEH,i | ||||
| Frequenz | Rad mit einem Durchmesser von 920 mm, keine Messung | Rad mit einem Durchmesser von 840 mm, keine Messung | Rad mit einem Durchmesser von 680 mm, keine Messung | Rad mit einem Durchmesser von 1.200 mm, keine Messung |
| 50 Hz | 75,4 | 75,4 | 75,4 | 75,4 |
| 63 Hz | 77,3 | 77,3 | 77,3 | 77,3 |
| 80 Hz | 81,1 | 81,1 | 81,1 | 81,1 |
| 100 Hz | 84,1 | 84,1 | 84,1 | 84,1 |
| 125 Hz | 83,3 | 82,8 | 82,8 | 82,8 |
| 160 Hz | 84,3 | 83,3 | 83,3 | 83,3 |
| 200 Hz | 86,0 | 84,1 | 83,9 | 84,5 |
| 250 Hz | 90,1 | 86,9 | 86,3 | 90,4 |
| 315 Hz | 89,8 | 87,9 | 88,0 | 90,4 |
| 400 Hz | 89,0 | 89,9 | 92,2 | 89,9 |
| 500 Hz | 88,8 | 90,9 | 93,9 | 90,1 |
| 630 Hz | 90,4 | 91,5 | 92,5 | 91,3 |
| 800 Hz | 92,4 | 91,5 | 90,9 | 91,5 |
| 1.000 Hz | 94,9 | 93,0 | 90,4 | 93,6 |
| 1.250 Hz | 100,4 | 98,7 | 93,2 | 100,5 |
| 1.600 Hz | 104,6 | 101,6 | 93,5 | 104,6 |
| 2.000 Hz | 109,6 | 107,6 | 99,6 | 115,6 |
| 2.500 Hz | 114,9 | 111,9 | 104,9 | 115,9 |
| 3.150 Hz | 115,0 | 114,5 | 108,0 | 116,0 |
| 4.000 Hz | 115,0 | 114,5 | 111,0 | 116,0 |
| 5.000 Hz | 115,5 | 115,0 | 111,5 | 116,5 |
| 6.300 Hz | 115,6 | 115,1 | 111,6 | 116,6 |
| 8.000 Hz | 116,0 | 115,5 | 112,0 | 117,0 |
| 10.000 Hz | 116,7 | 116,2 | 112,7 | 117,7 |
(Stand: 28.07.2021)
|
LH,VEH,SUP,i | |
| Frequenz | Fahrzeugtyp |
| a | |
| EU-Norm | |
| 50 Hz | 0,0 |
| 63 Hz | 0,0 |
| 80 Hz | 0,0 |
| 100 Hz | 0,0 |
| 125 Hz | 0,0 |
| 160 Hz | 0,0 |
| 200 Hz | 0,0 |
| 250 Hz | 0,0 |
| 315 Hz | 0,0 |
| 400 Hz | 0,0 |
| 500 Hz | 0,0 |
| 630 Hz | 0,0 |
| 800 Hz | 0,0 |
| 1.000 Hz | 0,0 |
| 1.250 Hz | 0,0 |
| 1.600 Hz | 0,0 |
| 2.000 Hz | 0,0 |
| 2.500 Hz | 0,0 |
| 3.150 Hz | 0,0 |
| 4.000 Hz | 0,0 |
| 5.000 Hz | 0,0 |
| 6.300 Hz | 0,0 |
| 8.000 Hz | 0,0 |
| 10.000 Hz | 0,0 |
Tabelle G-4: Koeffizienten LR,IMPACT,i für Stoßgeräusche 21
| "LR,IMPACT,i | |
| Wellenlänge | Einzelne(r) Weiche/Stoß/Kreuzung/100 m |
| 2.000 mm | 22,0 |
| 1.600 mm | 22,0 |
| 1.250 mm | 22,0 |
| 1.000 mm | 22,0 |
| 800 mm | 22,0 |
| 630 mm | 20,0 |
| 500 mm | 16,0 |
| 400 mm | 15,0 |
| 315 mm | 14,0 |
| 250 mm | 15,0 |
| 200 mm | 14,0 |
| 160 mm | 12,0 |
| 125 mm | 11,0 |
| 100 mm | 10,0 |
| 80 mm | 9,0 |
| 63 mm | 8,0 |
| 50 mm | 6,0 |
| 40 mm | 3,0 |
| 31,5 mm | 2,0 |
| 25 mm | -3,0 |
| 20 mm | -8,0 |
| 16 mm | -13,0 |
| 12,5 mm | -17,0 |
| 10 mm | -19,0 |
| 8 mm | -22,0 |
| 6,3 mm | -25,0 |
| 5 mm | -26,0 |
| 4 mm | -32,0 |
| 3,15 mm | -35,0 |
| 2,5 mm | -40,0 |
| 2 mm | -43,0 |
| 1,6 mm | -45,0 |
| 1,25 mm | -47,0 |
| 1 mm | -49,0 |
| 0,8 mm | -50,0 |
Tabelle G-5: Koeffizienten LW,0,idling für Antriebsgeräusche 21
(Red. Anm.: Änd.aus der RL (EU) 2021/1226 Punkt (20)(f) ist nicht eingearbeitet, Spaltenzahl ist unklar)
(Werte sind ausgedrückt in Schallleistungspegel pro Fahrzeug)
|
LW,0,idling | ||||||||||
| Frequenz |
Fahrzeugtyp | |||||||||
| d | d | d | e | e | ||||||
| Diesellokomotive (c. 800 kW) | Diesellokomotive (c. 2.200 kW) | Dieseltriebwagen | Elektrolokomotive | Elektrotriebwagen | ||||||
| Quelle A | Quelle B | Quelle A | Quelle B | Quelle A | Quelle B | Quelle A | Quelle B | Quelle A | Quelle B | |
| 50 Hz | 98,9 | 103,2 | 99,4 | 103,7 | 82,6 | 86,9 | 87,9 | 92,2 | 80,5 | 84,8 |
| 63 Hz | 94,8 | 100,0 | 107,3 | 112,5 | 82,5 | 87,7 | 90,8 | 96,0 | 81,4 | 86,6 |
| 80 Hz | 92,6 | 95,5 | 103,1 | 106,0 | 89,3 | 92,2 | 91,6 | 94,5 | 80,5 | 83,4 |
| 100 Hz | 94,6 | 94,0 | 102,1 | 101,5 | 90,3 | 89,7 | 94,6 | 94,0 | 82,2 | 81,6 |
| 125 Hz | 92,8 | 93,3 | 99,3 | 99,8 | 93,5 | 94,0 | 94,8 | 95,3 | 80,0 | 80,5 |
| 160 Hz | 92,8 | 93,6 | 99,3 | 100,1 | 99,5 | 100,3 | 96,8 | 97,6 | 79,7 | 80,5 |
| 200 Hz | 93,0 | 92,9 | 99,5 | 99,4 | 98,7 | 98,6 | 104,0 | 103,9 | 79,6 | 79,5 |
| 250 Hz | 94,8 | 92,7 | 101,3 | 99,2 | 95,5 | 93,4 | 100,8 | 98,7 | 96,4 | 94,3 |
| 316 Hz | 94,6 | 92,4 | 101,1 | 98,9 | 90,3 | 88,1 | 99,6 | 97,4 | 80,5 | 78,3 |
| 400 Hz | 95,7 | 92,8 | 102,2 | 99,3 | 91,4 | 88,5 | 101,7 | 98,8 | 81,3 | 78,4 |
| 500 Hz | 95,6 | 92,8 | 102,1 | 99,3 | 91,3 | 88,5 | 98,6 | 95,8 | 97,2 | 94,4 |
| 630 Hz | 98,6 | 96,8 | 101,1 | 99,3 | 90,3 | 88,5 | 95,6 | 93,8 | 79,5 | 77,7 |
| 800 Hz | 95,2 | 92,7 | 101,7 | 99,2 | 90,9 | 88,4 | 95,2 | 92,7 | 79,8 | 77,3 |
| 1.000 Hz | 95,1 | 93,0 | 101,6 | 99,5 | 91,8 | 89,7 | 96,1 | 94,0 | 86,7 | 84,6 |
| 1.250 Hz | 95,1 | 92,9 | 99,3 | 97,1 | 92,8 | 90,6 | 92,1 | 89,9 | 81,7 | 79,5 |
| 1.600 Hz | 94,1 | 93,1 | 96,0 | 95,0 | 92,8 | 91,8 | 89,1 | 88,1 | 82,7 | 81,7 |
| 2.000 Hz | 94,1 | 93,2 | 93,7 | 92,8 | 90,8 | 89,9 | 87,1 | 86,2 | 80,7 | 79,8 |
| 2.500 Hz | 99,4 | 98,3 | 101,9 | 100,8 | 88,1 | 87,0 | 85,4 | 84,3 | 78,0 | 76,9 |
| 3.160 Hz | 92,5 | 91,5 | 89,5 | 88,5 | 85,2 | 84,2 | 83,5 | 82,5 | 75,1 | 74,1 |
| 4.000 Hz | 89,5 | 88,7 | 87,1 | 86,3 | 83,2 | 82,4 | 81,5 | 80,7 | 72,1 | 71,3 |
| 5.000 Hz | 87,0 | 86,0 | 90,5 | 89,5 | 81,7 | 80,7 | 80,0 | 79,0 | 69,6 | 68,6 |
| 6.350 Hz | 84,1 | 83,4 | 31,4 | 30,7 | 78,8 | 78,1 | 78,1 | 77,4 | 66,7 | 66,0 |
| 8.000 Hz | 81,5 | 80,9 | 81,2 | 80,6 | 76,2 | 75,6 | 76,5 | 75,9 | 64,1 | 63,5 |
| 10.000 Hz | 79,2 | 78,7 | 79,6 | 79,1 | 73,9 | 73,4 | 75,2 | 74,7 | 61,8 | 61,3 |
Tabelle G-6: Koeffizienten LW,0,1, LW,0,2, α1, α2 für aerodynamische Geräusche 21
(Werte sind ausgedrückt in Schallleistungspegel pro Fahrzeug (für ein 20 m langes Fahrzeug))
| Aerodynamische Geräusche bei 300 km/h | ||
| α1 | α2 | |
| 50 | 50 | |
| Frequenz | LW,0,1 | LW,0,2 |
| 50 Hz | 112,6 | 36,7 |
| 63 Hz | 113,2 | 38,5 |
| 80 Hz | 115,7 | 39,0 |
| 100 Hz | 117,4 | 37,5 |
| 125 Hz | 115,3 | 36,8 |
| 160 Hz | 115,0 | 37,1 |
| 200 Hz | 114,9 | 36,4 |
| 250 Hz | 116,4 | 36,2 |
| 315 Hz | 115,9 | 35,9 |
| 400 Hz | 116,3 | 36,3 |
| 500 Hz | 116,2 | 36,3 |
| 630 Hz | 115,2 | 36,3 |
| 800 Hz | 115,8 | 36,2 |
| 1.000 Hz | 115,7 | 36,5 |
| 1.250 Hz | 115,7 | 36,4 |
| 1.600 Hz | 114,7 | 105,2 |
| 2.000 Hz | 114,7 | 110,3 |
| 2.500 Hz | 115,0 | 110,4 |
| 3.150 Hz | 114,5 | 105,6 |
| 4.000 Hz | 113,1 | 37,2 |
| 5.000 Hz | 112,1 | 37,5 |
| 6.300 Hz | 110,6 | 37,9 |
| 8.000 Hz | 109,6 | 38,4 |
| 10.000 Hz | 108,8 | 39,2 |
Tabelle G-7: Koeffizienten Cbridge für bauliche Abstrahlung 21
| LH,bridge,i | ||
| Frequenz | +10 dB(A) | +15 dB(A) |
| 50 Hz | 85,2 | 90,1 |
| 63 Hz | 87,1 | 92,1 |
| 80 Hz | 91,0 | 96,0 |
| 100 Hz | 94,0 | 99,5 |
| 125 Hz | 94,4 | 99,9 |
| 160 Hz | 96,0 | 101,5 |
| 200 Hz | 92,5 | 99,6 |
| 250 Hz | 96,7 | 103,8 |
| 315 Hz | 97,4 | 104,5 |
| 400 Hz | 99,4 | 106,5 |
| 500 Hz | 100,7 | 107,8 |
| 630 Hz | 102,5 | 109,6 |
| 800 Hz | 107,1 | 116,1 |
| 1.000 Hz | 109,8 | 118,8 |
| 1.250 Hz | 112,0 | 120,9 |
| 1.600 Hz | 107,2 | 109,5 |
| 2.000 Hz | 106,8 | 109,1 |
| 2.500 Hz | 107,3 | 109,6 |
| 3.150 Hz | 99,3 | 102,0 |
| 4.000 Hz | 91,4 | 94,1 |
| 5.000 Hz | 86,9 | 89,6 |
| 6.300 Hz | 79,7 | 83,6 |
| 8.000 Hz | 75,1 | 79,0 |
| 10.000 Hz | 70,8 | 74,7 |
| Datenbank für Quellen von Industrie- und Gewerbelärm | Anlage H |
Diese Anlage enthält Beispiele für Eingangswerte für einige industrielle Lärmquellen, die zur Berechnung von Industrie- und Gewerbelärm nach dem unter Punkt 2.4 "Industrie- und Gewerbelärm" beschriebenen Verfahren herangezogen können. Da die Quellen von Industrie- und Gewebelärm spezifisch für den jeweiligen Industriestandort sind, sind die zutreffenden Werte von lokalen, nationalen oder internationalen Datenbanken oder durch Messungen zu gewinnen, je nachdem, was am geeignetsten ist.
Tabelle H-1: Koeffizienten LW, LW' und ΔLW,dir,xyz (x, y, z) für die Schallleistung
ΔLW,dir,xyz (x, y, z)=0
LW' wird als Schallleistung pro Meter bei Linienquellen und pro Quadratmeter bei Flächenquellen ausgedrückt.
| Beschreibung | Art der Quelle | Richtverhalten der Quelle | 63 | 125 | 250 | 500 | 1.000 | 2.000 | 4.000 | 8.000 |
| Strahlen im Freien - mit Düse | Punktquelle | Freies Feld | 108,77 | 110,37 | 112,77 | 107,77 | 104,37 | 98,07 | 97,07 | 86,97 |
| Drehofen | Linienquelle | Freies Feld | 79,27 | 84,17 | 86,67 | 89,27 | 93,07 | 93,47 | 92,07 | 87,77 |
| Werft | Flächenquelle | Halbkugel | 67,17 | 69,07 | 74,57 | 62,17 | 63,97 | 66,77 | 70,97 | 68,07 |
| Gasterminal | Flächenquelle | Halbkugel | 74,17 | 70,07 | 65,57 | 64,17 | 59,97 | 57,77 | 51,97 | 56,07 |
 | weiter . |  |