

umwelt-online: DIN 1045-1 Tragwerke aus Beton, Stahlbeton und Spannbeton; Bemessung und Konstruktion (3)
 | zurück |  |
7 Grundlagen zur Ermittlung der Schnittgrößen
7.1 Anforderungen
(1) Alle Berechnungsverfahren der Schnittgrößenermittlung müssen sicherstellen, dass die Gleichgewichtsbedingungen erfüllt sind.
(2) Wenn die Verträglichkeitsbedingungen nicht unmittelbar für die jeweiligen Grenzzustände nachgewiesen werden, muss sichergestellt werden, dass das Tragwerk bis zum Erreichen des Grenzzustandes der Tragfähigkeit ausreichend verformungsfähig ist und ein unzulässiges Verhalten im Grenzzustand der Gebrauchstauglichkeit ausgeschlossen ist.
(3) Der Gleichgewichtszustand wird im Allgemeinen am nichtverformten Tragwerk nachgewiesen (Theorie I. Ordnung). Wenn jedoch die Auslenkungen zu einem wesentlichen Anstieg der Schnittgrößen führen, muss der Gleichgewichtszustand am verformten Tragwerk nachgewiesen werden (Theorie II. Ordnung).
(4) Die Auswirkungen zeitlicher Einflüsse (z.B. Kriechen, Schwinden des Betons) auf die Schnittgrößen sind zu berücksichtigen, wenn sie von Bedeutung sind.
(5) Bei Bauteilen des üblichen Hochbaus dürfen die folgenden Vereinfachungen getroffen werden:
(6) Für Tragwerke mit vorwiegend ruhender Belastung dürfen die Auswirkungen der Belastungsgeschichte im Allgemeinen vernachlässigt werden, und es darf von einer gleichmäßigen Steigerung der Belastung ausgegangen werden.
7.2 Imperfektionen
(1) Für die Nachweise im Grenzzustand der Tragfähigkeit sind mit Ausnahme der außergewöhnlichen Bemessungssituationen ungünstige Auswirkungen möglicher Imperfektionen des unbelasteten Tragwerks zu berücksichtigen.
(2) Die einzelnen aussteifenden Bauteile sind für Schnittgrößen zu bemessen, die sich aus der Berechnung am Gesamttragwerk ergeben, wobei die Auswirkungen der Einwirkungen und Imperfektionen am Tragwerk als Ganzem einzubeziehen sind.
(3) Der Einfluss der Tragwerksimperfektionen darf durch den Ansatz geometrischer Ersatzimperfektionen erfasst werden.
(4) Bei der Schnittgrößenermittlung am Tragwerk als Ganzem dürfen die Auswirkungen der Imperfektionen über eine Schiefstellung des Tragwerks gegen die Sollachse um den Winkel αa1berücksichtigt werden:
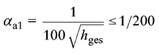 | (4) |
Dabei ist
| αa1 | der Winkel der Schiefstellung, in Bogenmaß |
| hges | die Gesamthöhe des Tragwerks, in m |
(5) Sind mehrere lastabtragende Bauteile nebeneinander vorhanden, darf αa1 nach Gleichung (4) mit dem Faktor αn abgemindert werden:
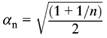 | (5) |
Dabei ist
| n | die Anzahl der lotrechten, lastabtragenden, in einem Geschoss nebeneinander liegenden Bauteile |
Als lastabtragend gelten die lotrechten Bauteile dann, wenn sie mindestens 70 % des Bemessungswerts der mittleren Längskraft NEd, m = FEd/n aufnehmen, worin FEd die Summe der Bemessungswerte der Längskräfte aller nebeneinander liegenden lotrechten Bauteile im betrachteten Geschoss bezeichnet.
(6) Alternativ zu Absatz (4) dürfen die Abweichungen von der Sollachse für die Bemessung des Gesamttragwerks sowie der aussteifenden Bauteile, Auflager und etwaig vorhandener Ringanker durch die Wirkung äquivalenter Horizontalkräfte ersetzt werden (siehe Bild 1 b) und d)).
(7) Bauteile, die Stabilisierungskräfte von den auszusteifenden Tragwerksteilen zu den aussteifenden Bauteilen übertragen, sollten für die Aufnahme einer zusätzlichen Horizontalkraft Hfd (siehe Bild 1e)) bemessen werden.
| Hfd = (Nbc + Nba) * αa2 | (6) |
| mit | |
| αa2 = 0,008 / (2k)0,5 in Bogenmaß | (7) |
Dabei ist
| k | die Anzahl der auszusteifenden Tragwerksteile im betrachteten Geschoss |
| Nbc, Nba | der jeweils unter Berücksichtigung der Imperfektionen ermittelte Bemessungswert der Längskraft in Stützen oder Wänden, die an das horizontale lastübertragende Bauteil grenzen (siehe Bild 1e)) |
Die Horizontalkräfte Hfd sind als eigenständige Einwirkungen zu betrachten und dürfen nicht zusätzlich durch Kombinationsbeiwerte ab gemindert werden, da diese bereits in den vertikalen Längskräften berücksichtigt sind. Die Horizontalkräfte Hfd brauchen für die Bemessung der vertikalen aussteifenden Bauteile nicht in Rechnung gestellt zu werden.
Bild 1 - Berücksichtigung der geometrischen Ersatzimperfektionen
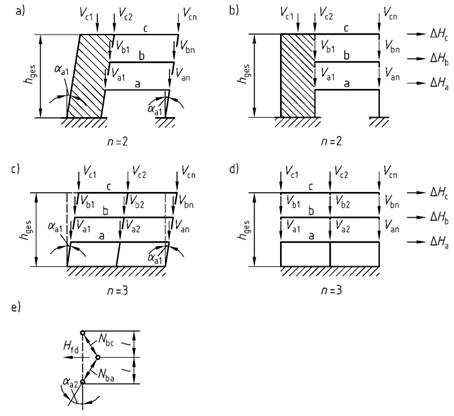
Legende
| a), c) | Berücksichtigung von Imperfektionen über Schiefstellung des Tragwerks |
| b), d) | Berücksichtigung von Imperfektionen über äquivalente Horizontalkräfte |
| e) | Berücksichtigung zusätzlicher Horizontalkräfte in Bauteilen nach Absatz (7) |
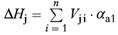 |
7.3 Idealisierungen und Vereinfachungen
7.3.1 Mitwirkende Plattenbreite, Lastausbreitung und effektive Stützweite
(1) Bei Plattenbalken ist die mitwirkende Plattenbreite von den Gurt- und Stegabmessungen, von der Art der Belastung, der Stützweite, den Auflagerbedingungen und der Querbewehrung abhängig. Die folgenden Regeln sind für alle Nachweise im Grenzzustand der Gebrauchstauglichkeit anwendbar und stellen für die Nachweise im Grenzzustand der Tragfähigkeit im Allgemeinen eine genügend genaue Abschätzung dar.
(2) Die mitwirkende Plattenbreite beff für Plattenbalken darf für Biegebeanspruchung infolge annähernd gleichmäßig verteilter Einwirkungen angenommen werden zu:
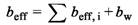 | (8) |
| mit | |
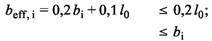 | (9) |
Dabei ist
| l0 | die wirksame Stützweite |
| bi | die tatsächlich vorhandene Gurtbreite |
| bw | die Stegbreite |
Bild 2 - Definition der mitwirkenden Breite beff
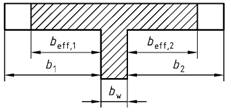
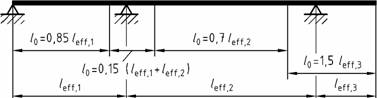
(3) Für annähernd gleichmäßig verteilte Einwirkungen darf die wirksame Stützweite l0 (entspricht dem Abstand der Momentennullpunkte) bei etwa gleichen Steifigkeitsverhältnissen der Einzelfelder vereinfachend Bild 3 entnommen werden.
Bild 3 - Angenäherte wirksame Stützweiten 10 zur Berechnung der mitwirkenden Plattenbreite
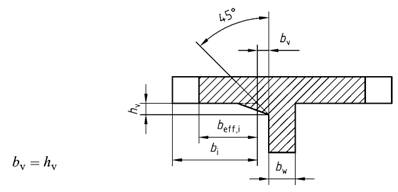
(4) Bei Platten mit veränderlicher Dicke darf die Stegbreite bw in Gleichung (8) um die Breite bv nach Bild 4 erhöht werden.
Bild 4 - Wirksame Stegbreite (bw + bv) bei Platten mit veränderlicher Dicke
(5) In der Lastausbreitungszone konzentriert eingeleiteter Längskräfte darf die wirksame Breite auf der Grundlage der Elastizitätstheorie bestimmt werden. Alternativ dazu darf ein Ausbreitungswinkel der Kräfte von β = 35° angenommen werden (siehe Bild 5). Dieser Winkel darf auch für die Lastausbreitung der Verankerungskräfte bei Vorspannung im nachträglichen oder ohne Verbund angesetzt werden (siehe Bild 6).
Bild 5 - Ausbreitungswinkel konzentriert eingeleiteter Längskräfte
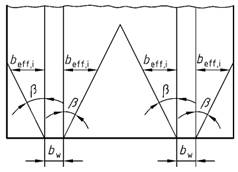
Bild 6 - Ausbreitung von Vorspannkräften am Beispiel eines Plattenbalkens
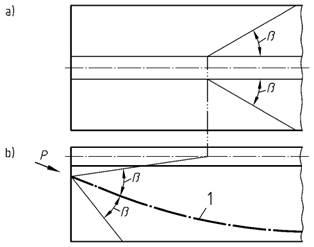
Legende
| a) | Draufsicht |
| b) | Ansicht |
| 1 | Spanngliedachse |
(6) Die effektive Stützweite leff eines Bauteils (Balken, Platte) darf wie folgt bestimmt werden:
| leff = ln + a1 + a2 | (10) |
Dabei ist
| ln | der lichte Abstand zwischen den Auflagervorderkanten |
| a1, a2 | der jeweilige Abstand zwischen den Auflagervorderkanten und den rechnerischen Auflagerlinien des betrachteten Feldes |
Die Werte für a1 und a2 sind von den Auflager- und Einspannbedingungen des Bauteils abhängig und sind in geeigneter Weise festzulegen (siehe z.B. Bild 7). 5)
Bild 7 - Beispiele für die Bestimmung der effektiven Stützweite eines Bauteils (Balken, Platte)
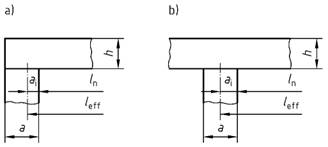
Legende
| a) nicht durchlaufende Bauteile |  |
| b) durchlaufende Bauteile | 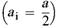 |
(7) Im Fall einer direkten Lagerung wird die Auflagerkraft des gestützten Bauteils durch Druckspannungen am unteren Querschnittsrand des Bauteils aufgenommen. Bei monolithischer Verbindung darf dies angenommen werden, wenn der Abstand der Unterkante des gestützten Bauteils zur Unterkante des stützenden Bauteils größer ist als die Höhe des gestützten Bauteils. Andernfalls ist von einer indirekten Lagerung auszugehen (siehe Bild 8).
Bild 8 - Definition der direkten und indirekten Lagerung
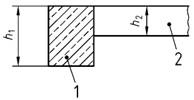
Legende
| 1 | stützendes Bauteil |
| 2 | gestützes Bauteil |
| (h1 - h2) > h2 | |
| (h1 - h2) < h2 |
7.3.2 Sonstige Vereinfachungen
(1) Durchlaufende Platten und Balken dürfen im üblichen Hochbau unter der Annahme frei drehbarer Lagerung berechnet werden.
(2) Der Bemessungswert des Stützmoments durchlaufender Balken oder Platten, deren Auflager als frei drehbar angesehen werden können, darf unabhängig vom angewendeten Rechenverfahren um einen Betrag ΔMEd reduziert werden, wenn bei der Berechnung der Stützmomente als effektive Stützweite der Abstand zwischen den Auflagermitten angenommen wird:
| ΔMEd = CEd * a/8 | (11) |
Dabei ist
| CEd | der Bemessungswert der Auflagerreaktion |
| a | die Auflagerbreite |
(3) Wenn ein Balken oder eine Platte über einem Auflager durchläuft und mit diesem monolithisch verbunden ist, darf als Bemessungsmoment das Moment am Auflagerrand zugrunde gelegt werden, wobei jedoch der Mindestwert nach 8.2 (5) nicht unterschritten werden sollte.
(4) Die Stützkräfte aus den Auflagerreaktionen von einachsig gespannten Platten, Rippendecken und Balken (einschließlich Plattenbalken) dürfen unter der Annahme ermittelt werden, dass die Bauteile (unter Vernachlässigung der Durchlaufwirkung) frei drehbar gelagert sind. Die Durchlaufwirkung sollte jedoch stets für das erste Innenauflager sowie solche Innenauflager berücksichtigt werden, bei denen das Stützweitenverhältnis benachbarter Felder mit annähernd gleicher Steifigkeit außerhalb des Bereichs 0,5 < leff,1 /leff, 2 < 2,0 liegt.
(5) Die maßgebenden Querkräfte dürfen bei üblichen Hochbauten für Vollbelastung aller Felder ermittelt werden, wenn das Stützweitenverhältnis benachbarter Felder mit annähernd gleicher Steifigkeit 0,5 < leff,1 /leff, 2 < 2,0 beträgt.
(6) In rahmenartigen Tragwerken des üblichen Hochbaus, bei denen alle horizontalen Kräfte von aussteifenden Scheiben aufgenommen werden, dürfen bei Innenstützen, die mit Balken oder Platten biegefest verbunden sind, die Biegemomente aus Rahmenwirkung vernachlässigt werden, wenn das Stützweitenverhältnis benachbarter Felder mit annähernd gleicher Steifigkeit 0,5 < leff, 1 /leff, 2 < 2,0 beträgt.
(7) Randstützen von rahmenartigen Tragwerken sind stets als Rahmenstiele in biegefester Verbindung mit Balken oder Platten zu berechnen. Dies gilt auch für Stahlbetonwände in Verbindung mit Platten.
(8) Rippen- oder Kassettendecken dürfen für die Schnittgrößenermittlung bei einem Verfahren nach 8.2 oder 8.3 als Vollplatten betrachtet werden, wenn die Gurtplatte zusammen mit den Rippen eine ausreichende Torsionssteifigkeit besitzt. Dies darf vorausgesetzt werden, wenn gleichzeitig
(9) Decken aus Rippen und Zwischenbauteilen ohne Aufbeton dürfen für die Schnittgrößenermittlung bei einem Verfahren nach 8.2 oder 8.3 als Vollplatten angesehen werden, wenn Querrippen in einem Abstand sT angeordnet werden, der die Werte der Tabelle 5 nicht überschreitet.
Tabelle 5 - Größter Querrippenabstand sT bei Decken aus Rippen und Zwischenbauteilen ohne Aufbeton
| Zeile | Spalte | 1 | 2 | |
| Achsabstand der Längsrippen sL | ||||
| sL < leff / 8 | sL > leff / 8 | |||
| 1 | Gebäudeart | Wohngebäude | - | 12h |
| 2 | andere Gebäude | 10h | 8h | |
| leff | effektive Stützweite der Längsrippen |
| h | Gesamtdicke der Rippendecke |
8 Verfahren zur Ermittlung der Schnittgrößen
8.1 Allgemeines
(1) Jedes Berechnungsverfahren muss im angegebenen Anwendungsbereich das geforderte Zuverlässigkeitsniveau dieser Norm sicherstellen. Diese Anforderung gilt bei Einhaltung der in 8.1 bis 8.7 aufgeführten Regeln als erfüllt.
(2) Sofern relevant, ist der Einfluss der Torsionssteifigkeit bei der Schnittgrößenermittlung angemessen zu berücksichtigen.
(3) Das linear-elastische Verfahren verwendet eine lineare Schnittgrößen-Verformungs-Beziehung.
(4) Verfahren der Plastizitätstheorie verwenden im Allgemeinen eine ideal-elastisch-plastische oder eine ideal-starr-plastische Schnittgrößen-Verformungs-Beziehung.
(5) Der Ausdruck "nichtlineare Berechnung" bezieht sich auf Berechnungsverfahren, die nichtlineare Schnittgrößen-Verformungs-Beziehungen berücksichtigen (physikalisch nichtlinear). Verfahren, bei denen das Gleichgewicht unter Berücksichtigung der Tragwerksverformungen nachgewiesen wird, werden als "Berechnung nach Theorie II. Ordnung" bezeichnet (geometrisch nichtlinear).
8.2 Linear-elastische Berechnung
(1) Grundlage der linear-elastischen Berechnung sind die Steifigkeiten der ungerissenen Querschnitte (Zustand I). Es dürfen jedoch auch die Steifigkeiten der gerissenen Querschnitte (Zustand II) verwendet werden.
(2) Die Anwendung des linear-elastischen Berechnungsverfahrens erfordert im Allgemeinen keine besonderen Maßnahmen zur Sicherstellung angemessener Verformungsfähigkeit, sofern sehr hohe Bewehrungsgrade in den kritischen Abschnitten der Bauteile vermieden und die Anforderungen dieser Norm bezüglich einer Mindestbewehrung erfüllt werden.
(3) Für Durchlaufträger, bei denen das Stützweitenverhältnis benachbarter Felder mit annähernd gleichen Steifigkeiten 0,5 < leff, 1 /leff, 2 < 2,0 beträgt, in Riegeln von Rahmen und in sonstigen Bauteilen, die vorwiegend auf Biegung beansprucht sind, einschließlich durchlaufender, in Querrichtung kontinuierlich gestützter Platten, sollte das Verhältnis x/d den Wert 0,45 für Beton bis zur Festigkeitsklasse C50/60 und den Wert 0,35 für Beton ab der Festigkeitsklasse C55/67 und für Leichtbeton nicht übersteigen, sofern keine geeigneten konstruktiven Maßnahmen zur Sicherstellung ausreichender Duktilität getroffen werden (siehe 13.1.1 (5)). Die Druckzonenhöhe x ist dabei mit den Bemessungswerten der Einwirkungen und der Baustofffestigkeiten zu ermitteln.
(4) Bei nicht vorgespannten Durchlaufträgern und -platten des üblichen Hochbaus brauchen - mit Ausnahme des Nachweises der Lagesicherheit nach DIN 1055-100-Bemessungssituationen mit günstigen ständigen Einwirkungen nicht berücksichtigt zu werden, wenn die Konstruktionsregeln für die Mindestbewehrung eingehalten werden.
(5) Zur Berücksichtigung einer vorgenommenen Idealisierung des Tragwerks und möglicher unbeabsichtigter Abweichungen des Tragsystems während der Bauzeit sollte das Bemessungsmoment in den Anschnitten vertikaler Auflager von Durchlaufträgern nicht geringer sein als 65 % des Moments bei Annahme voller Einspannung am Auflagerrand.
(6) Übliche Berechnungsverfahren für Plattenschnittgrößen mit Ansatz gleicher Steifigkeiten in beiden Richtungen gelten nur, wenn der Abstand der Längsbewehrung zur zugehörigen Querbewehrung in der Höhe 50 mm oder d/10 nicht überschreitet (der größere Wert ist maßgebend).
8.3 Linear-elastische Berechnung mit Umlagerung
(1) Die unter Verwendung des linear-elastischen Verfahrens nach 8.2 ermittelten Momente dürfen für die Nachweise in den Grenzzuständen der Tragfähigkeit umgelagert werden, wobei die sich daraus ergebenden Schnittgrößen mit den einwirkenden Lasten im Gleichgewicht stehen müssen.
(2) Die Auswirkungen einer Momentenumlagerung müssen bei der Bemessung durchgängig berücksichtigt werden. Dies gilt für die Bemessung für Biegung mit oder ohne Längskraft, für die Bemessung für Querkraft, für die Verankerungsregeln und für die Abstufung der Bewehrung.
(3) Für Durchlaufträger, bei denen das Stützweitenverhältnis benachbarter Felder mit annähernd gleicher Steifigkeit 0,5 < leff, 1 /leff, 2 < 2,0 beträgt, in Riegeln von unverschieblichen Rahmen und in sonstigen Bauteilen, die vorwiegend auf Biegung beansprucht sind, einschließlich durchlaufender, in Querrichtung kontinuierlich gestützter Platten, gelten für mögliche Momentenumlagerungen die folgenden Grenzen:
| δ > 0,64 + 0,8xd/d > 0,7 | bis C50/60 | (12) |
| δ > 0,72 + 0,8xd/d > 0,8 | ab C55/67 und Leichtbeton | (13) |
| δ > 0,64 + 0,8xd/d > 0,85 | bis C50/60 | (14) |
| δ = 1,0 (keine Umlagerung) | ab C55/67 und Leichtbeton |
Dabei ist
| δ | das Verhältnis des umgelagerten Moments zum Ausgangsmoment vor der Umlagerung |
| xd/d | die bezogene Druckzonenhöhe im Grenzzustand der Tragfähigkeit nach Umlagerung, berechnet mit den Bemessungswerten der Einwirkungen und der Baustofffestigkeiten |
Für die Eckknoten unverschieblicher Rahmen ist die Umlagerung auf δ = 0,9 begrenzt.
(4) Bei verschieblichen Rahmen ist keine Umlagerung zugelassen.
(5) Bei Tragwerken aus unbewehrtem Beton und solchen, die aus vorgefertigten Segmenten mit unbewehrten Kontaktfugen bestehen, ist keine Umlagerung zugelassen.
(6) Für die Ermittlung von Querkraft, Drillmoment und Auflagerreaktion bei Platten darf entsprechend dem Momentenverlauf nach Umlagerung eine lineare Interpolation zwischen den Beanspruchungen bei voll eingespanntem Rand und denen bei gelenkig gelagertem Rand vorgenommen werden.
8.4 Verfahren nach der Plastizitätstheorie
8.4.1 Allgemeines
(1) Verfahren der Schnittgrößenermittlung nach der Plastizitätstheorie sind bei vorwiegend biegebeanspruchten Bauteilen für die Nachweise im Grenzzustand der Tragfähigkeit anwendbar. Bei Bauteilen aus Leichtbeton sollten diese Verfahren nicht angewendet werden.
(2) Werden die Verträglichkeitsbedingungen nicht direkt überprüft, sind Verfahren auf der Grundlage der Plastizitätstheorie nur für Tragwerke mit gut verformungsfähigen Bauwerksteilen zulässig.
(3) Bei zweiachsig gespannten Platten sind Verfahren der Schnittgrößenermittlung, die plastische Gelenke ohne eine direkte Kontrolle ihrer Rotationsfähigkeit einschließen, nur dann zulässig, wenn die bezogene Druckzonenhöhe im Gelenkbereich an keiner Stelle und in keiner Richtung den Wert x/d = 0,25 für Beton bis zu einer Festigkeitsklasse C50/60 und den Wert x/d = 0,15 für Beton ab der Festigkeitsklasse C55/67 überschreitet und bei durchlaufenden Platten das Verhältnis von Stützmomenten zu Feldmomenten dabei zwischen 0,5 und 2,0 liegt. Die Druckzonenhöhe x ist dabei mit den Bemessungswerten der Einwirkungen und der Baustofffestigkeiten zu ermitteln. Werden diese Grenzen nicht eingehalten, ist die Rotationsfähigkeit nach 8.4.2 nachzuweisen.
(4) Stahl mit normaler Duktilität (siehe Tabelle 11) darf bei Anwendung der Plastizitätstheorie für stabförmige Bauteile und Platten nicht verwendet werden.
(5) Bei Scheiben dürfen Verfahren nach der Plastizitätstheorie stets (also auch bei Verwendung von Stahl mit normaler Duktilität) ohne direkten Nachweis des Rotationsvermögens angewendet werden.
(6) Verfahren nach der Plastizitätstheorie bilden auch die Grundlage für die Bemessung mit Stabwerkmodellen. Diese lassen sich sowohl für die Bemessung der ungestörten Bereiche von Balken und Platten im gerissenen Zustand (siehe 10.2 bis 10.4) als auch für die Bemessung und konstruktive Durchbildung von Diskontinuitätsbereichen (siehe 10.6) anwenden.
8.4.2 Vereinfachter Nachweis der plastischen Rotation bei vorwiegend biegebeanspruchten Bauteilen
(1) Das vereinfachte Verfahren für stabförmige Bauteile einschließlich einachsig gespannter Platten basiert auf dem Nachweis der Rotationsfähigkeit ausgezeichneter Stababschnitte mit einer Länge von etwa 1,2h, wobei vorausgesetzt wird, dass diese sich als erste unter der jeweils maßgebenden Einwirkungskombination plastisch verformen (Ausbildung plastischer Gelenke), so dass sie wie ein Querschnitt behandelt werden dürfen. Der Nachweis der plastischen Rotation im Grenzzustand der Tragfähigkeit gilt als erbracht, wenn nachgewiesen wird, dass die vorhandene Rotation θE den Bemessungswert der zulässigen Rotation θpl, d nicht überschreitet:
| θE < θpl, d | (15) |
(2) Für die Bereiche der plastischen Gelenke darf das Verhältnis x/d die Werte 0,45 für Beton bis zur Festigkeitsklasse C50/60 und 0,35 für Beton ab der Festigkeitsklasse C55/67 nicht überschreiten.
(3) Die vorhandene Rotation θE ist auf der Grundlage der Bemessungswerte der Einwirkungen und der Mittelwerte der Baustofffestigkeiten (siehe 8.5.1) sowie der mittleren Werte der Vorspannung zum maßgeblichen Zeitpunkt zu ermitteln.
(4) Wird die vorhandene Rotation θE eines plastischen Gelenks durch Integration der Krümmungen zwischen den Gelenken berechnet, ist im Allgemeinen die Anwendung einer vereinfachten trilinearen Momenten-Krümmungs-Beziehung nach 8.5.2 (3) ausreichend. Die Momente aus Vorspannung dürfen dabei als Einwirkung betrachtet werden.
(5) Die zulässige plastische Rotation darf vereinfachend durch Multiplikation des Grundwerts der zulässigen Rotation mit einem Korrekturfaktor kλ zur Berücksichtigung der Schubschlankheit ermittelt werden. Der Grundwert der zulässigen Rotation darf für Betonstahl mit hoher Duktilität und Betonfestigkeitsklassen bis C50/60 sowie C100/115 Bild 9 entnommen werden. Für Betonfestigkeitsklassen C55/67 bis C90/105 darf entsprechend interpoliert werden. Die abgelesenen Werte gelten für eine Schubschlankheit λ = 3,0 und sind für andere Werte von λ mit kλ zu multiplizieren.
| kλ = (λ /3)0,5 | (16) |
Dabei ist
| λ | das Verhältnis aus dem Abstand zwischen Momentennullpunkt und -maximum nach Umlagerung und der statischen Nutzhöhe d |
Vereinfacht darf λ dabei aus den Bemessungswerten des Biegemoments und der zugehörigen Querkraft berechnet werden:
| λ = MEd / (VEd * d) | (17) |
Angaben für eine genauere Ermittlung der zulässigen plastischen Rotation können DAfStb-Heft 525 entnommen werden.
Bild 9 - Grundwerte der zulässigen plastischen Rotation für Festigkeitsklassen des Betons C12/16 bis C50/60 und Cl00/115. (Die dargestellten Werte gelten unmittelbar für eine Schubschlankheit λ = 3,0.)
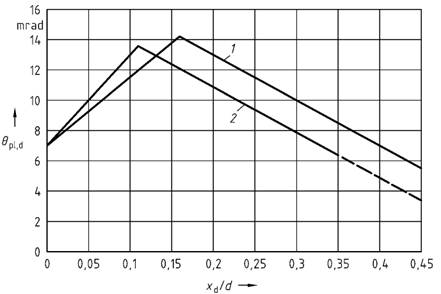
Legende
| 1 | für C12/16 bis C50/60 |
| 2 | für C100/115 |
8.5 Nichtlineare Verfahren
8.5.1 Allgemeines
(1) Nichtlineare Verfahren der Schnittgrößenermittlung dürfen sowohl für die Nachweise in den Grenzzuständen der Gebrauchstauglichkeit als auch der Tragfähigkeit angewendet werden, wobei die Gleichgewichts- und Verträglichkeitsbedingungen zu erfüllen sind.
(2) Durch die Festlegung der Bewehrung nach Größe und Lage schließen nichtlineare Verfahren die Bemessung für Biegung mit oder ohne Längskraft nach 10.2 ein.
(3) Die Formänderungen und Schnittgrößen des Tragwerks sind auf der Grundlage der Spannungs-Dehnungs-Linien für Beton (siehe Bild 22), Betonstahl (siehe Bild 26) und Spannstahl (siehe Bild 28) zu berechnen, wobei die Mittelwerte der Baustofffestigkeiten zugrunde zu legen sind.
(4) Die Mittelwerte der Baustofffestigkeiten dürfen rechnerisch wie folgt angenommen werden:
| fyR = 1,1 fyk | (18) | |
| ftR = 1,08 fyR | (für Betonstahl mit hoher Duktilität) | (19) |
| ftR = 1,05 fyR | (für Betonstahl mit normaler Duktiliät) | (20) |
| fp0,1 R = 1,1 fp0,1k | (21) | |
| fpR = 1,1 fpk | (22) | |
| fcR = 0,85 α
fck | (bis C50/60) | (23) |
| fcR = 0,85 α
fck/γc' | (ab C55/67) | (24) |
mit α nach 9.1.6 (2) bzw. 9.1.6 (4) und γ' nach 5.3.3 (9).
Hierbei sollte ein einheitlicher Teilsicherheitsbeiwert γR = 1,3 (für ständige und vorübergehende Bemessungssituationen und Nachweis gegen Ermüdung) oder γR = 1,1 (für außergewöhnliche Bemessungssituationen für den Bemessungswert des Tragwiderstands) berücksichtigt werden.
(5) Der Bemessungswert des Tragwiderstands darf nicht kleiner sein als der Bemessungswert der maßgebenden Einwirkungskombination.
(6) Der Grenzzustand der Tragfähigkeit gilt als erreicht, wenn in einem beliebigen Querschnitt des Tragwerks
(7) Die kritische Stahldehnung sollte auf den Wert εsu = 0,025 festgelegt werden. Die kritische Betondehnung εc1u ist Tabelle 9 und Tabelle 10 zu entnehmen.
(8) Die Mitwirkung des Betons auf Zug zwischen den Rissen (tension stiffening) ist zu berücksichtigen. Sie darf unberücksichtigt bleiben, wenn dies auf der sicheren Seite liegt.
(9) Die Auswahl eines geeigneten Verfahrens zur Berücksichtigung der Mitwirkung des Betons auf Zug sollte in Abhängigkeit von der jeweiligen Bemessungsaufgabe getroffen werden. 6)
 | weiter. |  |