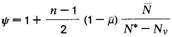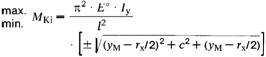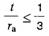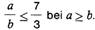umwelt-online: DIN 4113-1 - Konstruktion und Ausführung - Aluminiumkonstruktionen unter vorwiegend ruhender Belastung (3)

umwelt-online: DIN 4113-1 Aluminiumkonstruktionen unter vorwiegend ruhender Belastung; Konstruktion und Ausführung (3)

8.2 Nachweis nach Rechnungsgang

8.2.1 Einteilige Druckstäbe von gleichbleibendem Querschnitt (Biegeknicken)

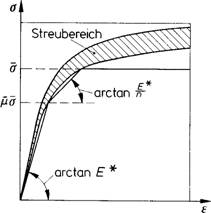
Das jeweilige σ-ε-Diagramm (Druck) der hier behandelten Aluminiumlegierungen wird nach Bild 2 durch einen dreiteiligen Sekantenzug, dessen Kennwerte aus Tabelle 10 zu entnehmen sind, genau genug erfasst.

Sowohl der planmäßig mittig als auch der planmäßig außermittig gedrückte und an beiden Enden gehaltene Stab kann nach Formel (1 a) berechnet werden, falls der Ausdruck

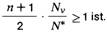
Falls der Ausdruck < 1 ist, gilt günstiger die Formel (1 b).

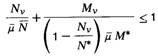	(1a)
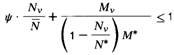
mit	(1b)

Ist das Verdrehen des zu untersuchenden Stabes verhindert (siehe auch Abschnitt 8.1.2), so ist in den Formeln (1 a) und (1b) bei Längsbelastung

n	Beiwert nach Tabelle 10

Tabelle 10. Festwerte für Sekantenzüge und Außermittigkeiten

	Legierung	̄σ N/mm²	E* N/mm²	μ	n	ungewollte Außermittigkeit u
	Legierung	̄σ N/mm²	E* N/mm²	μ	n	Rohre + I-Profile	-Profile
1	AlZn4,5Mg1 F35	290	68000	0,85	4,0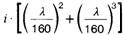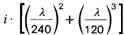
2	AIMgSi1 F 32	270	68000	0,85	4,0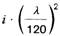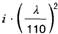
3	AlMgSi1 F28	210	65000	0,80	4,0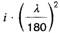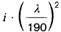
4	AlMgSi0,5 F22	170	65000	0,85	4,5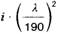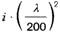
5	AlMg4,5Mn G31	230	65000	0,80	5,0
6a	AlMg4,5Mn F27/W28 Querschnitte aus Blech	130	65000	0,85	5,0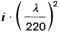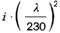
6b	AlMg4,5Mn F27 Rohre+ Profile	150	65000	0,85	5,0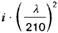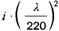
7	AlMg2Mn0,8 F24/G24/F25 AIMg3 F24/G24/F25	170	65000	0,85	4,5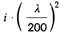
8	AlMg2Mn0,8 F20	110	60000	0,80	5,0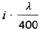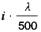
9	AlMg3 F18	80	55000	0,75	5,0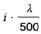
10	AlMg2Mn0,8 F/W19, F18 AlMg3 F/W19, F18	80	55000	0,75	5,0

Bild 2. (zu Tabelle 10)

N* =	N_E * = (π / S_ki )² x E* l (Eulerlast für Ausknicken in der Momentenebene mit der Knicklänge S_ki)
E*	rechnerischer Modul nach Tabelle 10
M*=	k̄σW_d (̄σ aus Tabelle 10)
k	charakteristischer, dem jeweiligen Querschnitt zugeordneter Rechenbeiwert (Tabelle 11)
W_d	auf den Biegedruckrand bezogenes Widerstandsmoment des unverschwächten Querschnitts des Stabes
̄N =	̄σ x A
A	unverschwächte Querschnittsfläche des Stabes
̄µ	Werkstoffbeiwert nach Tabelle 10
N_v =	v x N < N* mit N als Absolutwert der größten Druckkraft des Stabes
v	erforderlicher Sicherheitsfaktor v_H =1,5 für Lastfall H, v_HZ = 1,33 für Lastfall HZ. Bei Gerüstrohren ist v_H = 1,7 bzw. v_HZ = 1,5 zu setzen.
M_v =	v (a_M x M + N x u)
M =	\|M_i\| Absolutwert des maßgebenden Stabendmomentes, d.h. bei doppeltsymmetrischen Querschnitten (Tabelle 11, Spalten 2, 7, 8) M₂, bei einfach-symmetrischen Querschnitten (Tabelle 11, Spalten 3, 4, 5 und 6) ist neben M₂ auch M₁ zu verfolgen.
M₁, M₂	Stabendmomente, wobei \|M₂ > M₁\|
u	ungewollte Außermittigkeit nach Tabelle 10
a_M =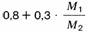

Weicht die Querschnittsform von denjenigen in Tabelle 11 ab und/oder liegen unverschiebliche Stabsysteme vor, so empfiehlt sich die Anwendung der Theorie II. Ordnung bis zum Erreichen des elastischen Grenzwertes der jeweils maßgebenden Randspannung (siehe auch Abschnitt 8.1.8, vergleiche auch DIN 4114 Teil 2, Ausgabe Februar 1953x, Ri 7.9 und Ri 10.2).

Bei ausschließlich planmäßig mittiger Beanspruchung und bei Einführung der Imperfektionen gemäß der niedrigsten Eigenfunktion, kann auch der Ersatzstabgedanke Anwendung finden.

Tabelle 11. Charakteristischer Rechenbeiwert k

1	2	3	4	5	6	7	8
Querschnitt, Lastangriff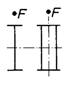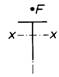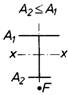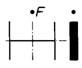
k-Werte	1,1	0,7	1,1		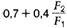1,1	1,25	1,2

Bei Längs- und Querbelastung von Stäben ist

a_M	1,1
M	max. \|M_Feld\| der größte Absolutwert des Biegemomentes zwischen dem ersten und dritten Viertelspunkt der Stablänge, soweit doppeltsymmetrische Querschnitte (nach Tabelle 11, Spalten 2, 7 und 8) vorliegen; bei einfach-symmetrischen Querschnitten ist für beide Momentenrichtungen der jeweilige Größtwert einzusetzen.

Für seitlich verschiebliche Rahmen vergleiche Abschnitt 8.2.4.

8.2.2 Biegedrillknicken

In den in Abschnitt 8.2.1 angegebenen Formeln (1a) und (1b) bedeuten bei Anwendung auf Biegedrillknicken

N*	der kleinere der beiden Werte N_E* (Eulerlast für Ausknicken in der Momentebene) bzw. N_Ki = π² x E* x A/λ²_Vi mit λ_Vi nach DIN 4114 Teil 2, Ausgabe Februar 1953x, Ri 7.5 bzw. Ri 10.1.
M*	nach Abschnitt 8.2.1 bzw. - wenn kleiner - \|M_Ki\| nach
	mit y_M, c, r_x nach Abschnitt 8.3.2.1. Das negative Vorzeichen der Wurzel ist anzuwenden, wenn bei einfach-symmetrischen Querschnitten aus dem Biegemoment Druckspannungen am Gurt mit dem kleineren I_yGurt auftreten. Das Querschnittskoordinatensystem ist so festzulegen, daß y_M > 0 ist. Wechselt die Momentenlinie innerhalb des Stabes das Vorzeichen und erzeugt das dem Absolutbetrag nach größere Moment max. M = \|M₂\| Druck am Flansch mit dem größeren I_yGurt, so sind die Nachweise nach den Formeln (1a) bzw. (1b) für beide Stabendmomente zu führen. Hierbei ist einmal für den M nach Abschnitt 8.2.1 \|M₂\| mit dem zugehörigen M_Ki (= max. M_Ki), zum anderen ist M = \|M₁\| mit dem zugehörigen M_Ki (= \|min. M_Ki\|) einzusetzen.
N_v
M_maßg	= \|M₁\| bzw. \|M₂\|, vergleiche unter M*
δ	δ ist der Abstand des Bezugspunktes B vom Schwerpunkt S in Richtung Schubmittelpunkt M (siehe Bild 3). Das Vorzeichen von M_maßg ist dasselbe wie für M_Ki, je nach Lastangriffspunkt in bezug auf B (statt bisher S) ist max. M_Ki bzw. min. M_Ki einzusetzen.
u	die für λ_y zu ermittelnde ungewollte Außermittigkeit (vergleiche Tabelle 10) Der Wert ψ ist mit den obengenannten Werten N* und N_Å zu berechnen.

Bild 3

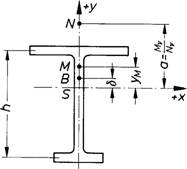
N	als Druckkraft positiv
B	Bezugspunkt für das Moment
M	Schubmittelpunkt
S	Schwerpunkt

8.2.3 Kippen von Trägern mit I-Querschnitt

Für den Fall der freien Kippung sowie bei Lastangriff zwischen Schubmittelpunkt und Zugflansch gilt (für einfache Balken) die Grundlage im Sinne der Abschnitte 8.2.1 und 8.2.2 mit den Sicherheitsfaktoren v_H = 1,7 und

v_HZ = 1,5, wobei N = 0 zu setzen ist, d.h.

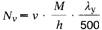
8.2.4 Bogen- und Rahmenknicken

Für verschiebliche Rahmen ist grundsätzlich ein Nachweis des stabilen Gleichgewichtes für v-fache Lasten am verformten System vorzunehmen (vergleiche auch Abschnitt 8.1.8). Soweit es sich hierbei um ein- und zweigeschossige verschiebliche Rahmen handelt, können - neben den Regelungen des Abschnittes 8.3.4 - auch Traglast-Nachweise geführt werden, die die spezifischen Eigenschaften der Aluminiumwerkstoffe berücksichtigen.

8.3 Nachweis nach Rechnungsgang II

8.3.1 Einteilige Druckstäbe von gleich bleibendem Querschnitt (Biegeknicken)

8.3.1.1 Planmäßig mittige Beanspruchung

Gerade, planmäßig mittig gedrückte Stäbe sind entsprechend DIN 4114 Teil 1, Ausgabe Juli 1952xx, Abschnitt 7, nachzuweisen.

Es muß

ω * N/A < zul σ

sein.

Hierin bedeuten:

N	Absolutwert der größten im Stab auftretenden Druckkraft
A	unverschwächte Querschnittsfläche des Stabes
ω	von der Aluminiumlegierung und dem Schlankheitsgrad abhängige Knickzahl. Bei nicht tabellierten Zwischenwerten von β_0,2 (Fußnoten Tabelle 1) darf näherungsweise linear zwischen zwei benachbarten Knickzahlentabellen interpoliert werden. Tabelle 12a gilt für Profile, Tabelle 12b gilt für Rundrohre mit und für Rechteckrohre mit einem Seitenverhältnis Bei Wanddickenunterschieden von mehr als 20 % gelten die Knickzahlen ω nach Tabelle 12a. Bei Hohlquerschnitten, die durch äußere Rippen versteift sind, darf mit einem Ersatzquerschnitt gerechnet werden, wobei die Innenkontur (r_i bzw. a_i und b_i) beizubehalten und die Wanddicke so zu berechnen ist, dass die Gesamtquerschnittsfläche erhalten bleibt. Für die äußere Verrippung gelten im übrigen die Begrenzungen h/t gemäß Bild 1 h und Tabelle 8a.
zul σ	für die gewählte Aluminiumlegierung geltende zulässige Druckspannung nach Tabelle 4. Für Rohre im Gerüstbau sind diese Werte im Verhältnis 1,5:1,7 bzw. 1,33:1,50 abzumindern.
λ	Schlankheitsgrad des Stabes entsprechend DIN 4114 Teil 1, Ausgabe Juli 1952xx, Abschnitt 7.1.

Für Stäbe mit λ < 20 ist kein Knicknachweis zu führen (also ist hier ω = 1).

Stäbe mit geringem Drillwiderstand sind, falls erforderlich, auf Drillknickung oder auf Biegedrillknickung nachzuweisen (siehe Abschnitt 8.1.2). Für Druckstäbe mit veränderlichem Querschnitt, veränderlicher Normalkraft oder elastischer Querstützung gilt DIN 4114 Teil 2, Ausgabe Februar 1953x, Ri 7.6 bis Ri 7.8 mit den Knickzahlen ω der Tabellen 12a und 12b vorliegender Norm.

Tabelle 12a. Knickzahlen ω für Profile

Werkstoffe	AlZn4,5Mg1 F35, F34					AlMgSi1 F30, F31, F32
Basiswert für Streckgrenze in N/mm²	280					260
Schlankheitsgrad λ	0	2	4	6	8	0	2	4	6	8
20	1	1,01	1,03	1,05	1,07	1	1	1,02	1,04	1,06
30	1,10	1,12	1,15	1,18	1,21	1,08	1,11	1,14	1,17	1,20
40	1,25	1,29	1,33	1,38	1,43	1,23	1,27	1,31	1,36	1,40
50	1,43	1,60	1,73	1,86	1,99	1,45	1,50	1,60	1,73	1,85
60	2,13	2,28	2,43	2,58	2,74	1,98	2,12	2,25	2,40	2,54
70	2,90	3,07	3,25	3,42	3,61	2,70	2,85	3,01	3,18	3,35
80	3,79	3,98	4,18	4,38	4,59	3,52	3,70	3,88	4,07	4,26
90	4,80	5,02	5,24	5,46	5,69	4,46	4,66	4,86	5,07	5,28
100	5,93	6,17	6,41	6,66	6,91	5,50	5,72	5,95	6,18	6,42
110	7,17	7,43	7,70	7,97	8,25	6,66	6,90	7,15	7,40	7,66
120	8,53	8,82	9,11	9,41	9,71	7,92	8,19	8,46	8,74	9,01
130	10,01	10,32	10,64	10,96	11,28	9,30	9,59	9,88	10,18	10,48
140	11,61	11,95	12,29	12,63	12,98	10,78	11,09	11,41	11,73	12,05
150	13,33	13,69	14,05	14,42	14,79	12,38	12,71	13,05	13,39	13,74
160	15,17	15,55	15,94	16,33	16,72	14,09	14,44	14,80	15,16	15,53
170	17,12	17,53	17,94	18,35	18,77	15,90	16,28	16,66	17,04	17,43
180	19,20	19,63	20,06	20,50	20,94	17,83	18,22	18,63	19,03	19,45
190	21,39	21,84	22,30	22,76	23,23	19,86	20,28	20,71	21,14	21,57
200	23,70	24,18	24,66	25,14	25,63	22,01	22,45	22,90	23,35	23,80
210	26,13	26,63	27,14	27,64	28,16	24,26	24,73	25,20	25,67	26,15
220	28,68	29,20	29,73	30,26	30,80	26,63	27,12	27,61	28,10	28,60
230	31,34	31,89	32,44	33,00	33,56	29,11	29,61	30,13	30,64	31,17
240	34,13	34,70	35,28	35,86	36,44	31,69	32,22	32,76	33,30	33,84
250	37,03					34,39

Fortsetzung Tabelle 12a.

Werkstoffe	AlMg4,5Mn G31 ¹) und AlMgSi1 F28					AIMg2Mn0,8 G24, F24, F25, AlMg3, AlMgSi0,5 F22
Basiswert für Streckgrenze in N/mm²	200					160
Schlankheitsgrad λ	0	2	4	6	8	0	2	4	6	8
20	1	1	1,02	1,04	1,06	1	1	1,02	1,04	1,05
30	1,08	1,10	1,13	1,15	1,18	1,08	1,10	1,13	1,15	1,18
40	1,21	1,24	1,28	1,31	1,34	1,20	1,23	1,25	1,27	1,30
50	1,38	1,42	1,47	1,52	1,57	1,33	1,37	1,41	1,45	1,49
60	1,63	1,71	1,82	1,94	2,06	1,53	1,58	1,62	1,66	1,71
70	2,18	2,30	2,43	2,57	2,70	1,76	1,82	1,87	1,96	2,06
80	2,84	2,99	3,14	3,29	3,44	2,17	2,28	2,39	2,50	2,62
90	3,60	3,76	3,93	4,10	4,27	2,74	2,87	2,99	3,12	3,25
100	4,44	4,62	4,81	4,99	5,18	3,39	3,52	3,66	3,80	3,95
110	5,38	5,57	5,78	5,98	6,19	4,10	4,25	4,40	4,56	4,71
120	6,40	6,61	6,83	7,06	7,28	4,88	5,04	5,21	5,38	5,55
130	7,51	7,74	7,98	8,22	8,46	5,72	5,90	6,08	6,26	6,45
140	8,71	8,96	9,22	9,47	9,73	6,64	6,83	7,02	7,22	7,42
150	10,00	10,27	10,54	10,81	11,09	7,62	7,82	8,03	8,24	8,45
160	11,38	11,66	11,95	12,25	12,54	8,67	8,89	9,11	9,33	9,56
170	12,84	13,15	13,45	13,77	14,08	9,79	10,02	10,25	10,49	10,73
180	14,44	14,72	15,05	15,37	15,71	10,97	11,22	11,46	11,71	11,97
190	16,04	16,38	16,73	17,07	17,42	12,22	12,48	12,74	13,01	13,27
200	17,78	18,13	18,49	18,86	19,23	13,54	13,82	14,09	14,37	14,65
210	19,60	19,97	20,35	20,73	21,12	14,93	15,22	15,51	15,80	16,09
220	21,51	21,90	22,30	22,70	23,10	16,39	16,69	16,99	17,29	17,60
230	23,51	23,92	24,33	24,75	25,17	17,91	18,22	18,54	18,86	19,18
240	25,60	26,03	26,46	26,89	27,33	19,50	19,83	20,16	20,49	20,82
250	27,77					21,16

weiter .